扩展功能
文章信息
- 李盛, 李建新, 王起才, 马莉, 董朝阳
- LI Sheng, LI Jian-xin, WANG Qi-cai, MA Li, DONG Zhao-yang
- 水泥砂浆封闭孔隙冻胀破坏问题的力学分析
- Mechanical Analysis of Frost Heawing Damage of Closed Pore in Cement Mortar
- 公路交通科技, 2015, Vol. 31 (4): 83-89
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 83-89
- 10.3969/j.issn.1002-0268.2015.04.015
-
文章历史
- 收稿日期:2013-12-26
2. 兰州工业学院 土木工程学院, 甘肃 兰州 730050;
3. 兰州铁路局兰州枢纽工程建设指挥部, 甘肃 兰州 730070
2. School of Civil Engineering, Lanzhou Institute of Technology, Lanzhou Gansu 730050, China;
3. Headquarters of Lanzhou Hub Construction, Lanzhou Railway Bureau, Lanzhou Gansu 730070, China
混凝土冻融破坏是指混凝土在正负温交替循环作用下,从表面开始发生开裂、剥落、强度降低,直到破坏的一种现象。西北严寒地区桥梁等混凝土结构物,尤其是那些处于干湿交替环境的桥梁墩台等下部结构,不同程度地遭到冻融破坏,从而严重影响了桥梁结构的正常使用,降低了桥梁安全性。众所周知,材料的破坏与否主要取决于荷载作用下材料内部的应力和应变大小。对多孔材料的冻融破坏归根结底也是一种力学行为,只有从力学分析方面出发才能加以阐明[1]。
美国学者T.C.Powers提出的静水压理论和渗透压理论[2, 3, 4],他认为吸水饱和的混凝土冻融破坏力主要由静水压力和渗透压力产生;Setzer[5, 6]、Scherer[7, 8]根据液态水、水蒸气和冰晶体三相平衡的热力学方程,提出了结晶压理论;刘希拉[9]、蔡昊[10]、商怀帅[11]基于疲劳累积损伤理论,分别提出了利用等效室内冻融循环次数和标准冻融试验数据预测现场混凝土冻融耐久性使用年限的方法、混凝土抗冻预测模型和混凝土结构冻融耐久性失效的随时模糊可靠度分析模型;巩妮娜[12]、郭利霞[13]采用有限元数值计算方法,从力学的角度研究了混凝土的冻融破坏;覃丽坤[14]、张众[15]、冀晓东[16]、商怀帅[17]、曹大富[18]建立了混凝土冻融损伤后的破坏准则,为遭受冻融循环作用的混凝土结构的计算分析提供强度判断依据和本构模型。这些工作从各自不同的角度推动混凝土冻融破坏的研究进展。实际上混凝土的冻融破坏跟孔结构特征有关。孔结构是混凝土细观结构的重要内容,它直接影响混凝土的许多性能(抗冻性、耐久性等)[19]。在国际上许多混凝土专家甚至把孔作为混凝土中的一个重要的组分[19, 20, 21]。而采用内压作用下孔洞膨胀损伤力学理论分析材料的力学行为对于混凝土材料抗冻耐久性的研究具有重要参考价值,且针对于含有内压的孔洞膨胀损伤问题已有大量研究[22, 23, 24]。然而混凝土中的毛细孔比较复杂,可能存在两端连通、两端封闭、一端连通的其中1种情况或者3种情况并存[25, 26],由于内部孔隙问题的复杂性,关于孔结构的冻胀破坏研究长期以来难以具体、深入。
本文从砂浆入手,根据热力学平衡原理,采用弹性力学方法及孔洞膨胀力学手段,仅对封闭孔隙在冻融作用下的孔隙应力进行细观力学计算分析,以期能够从力学分析角度更好地解释冻融对寒冷地区受冻结构物的破坏机制,为严寒地区桥梁工程的设计提供理论依据。
1 理论计算公式推导众所周知,水泥砂浆中的孔隙没有绝对意义上的全部封闭状态,仍与周围孔隙存在一定的连通性。混凝土的冻融破坏是由外及里,由大到小,当孔隙水结冰产生压力时,水能够从毛细管经过没有冰冻的孔扩散外逸至自由空间,缓解冻融过程中产生的冰胀压力和毛细孔水的渗透压力。当外界不断有水补给时,随着冻融次数、冻结压力的增加,水分不断向结构内部不同直径的孔隙迁移,孔隙不断被水分填塞。当孔隙含水率大于91.7%,且由于其周围介质的致密性导致其受冻时水分无法继续迁移时,将形成本文介绍的所谓封闭孔隙。为了明确其对内部结构的影响,分别从球形及圆柱形两种孔隙入手,推导了其在冻胀力作用下的孔隙应力。
1.1 封闭孔隙内表面压应力计算对于水泥砂浆饱水封闭孔隙,不考虑孔隙中水所含的其他微量物质,则封闭孔隙中的水可看作为单组份体系[27]。当温度降低时,封闭孔隙中的水结冰而产生膨胀,由于受到封闭孔隙孔壁的约束,而不能自由膨胀,若温度继续降低,只有部分水结成冰,另一部分水成过冷态,此时,封闭孔隙中水冰共存于孔隙中,达到平衡状态,遵从相数、温度、压力的关系。根据克拉贝龙方程得到作用于封闭孔隙内表面的均布压应力力ΔP为[28, 29]:
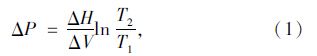
如前所述,水泥砂浆中的孔隙比较复杂,存在多种情况,本文主要针对封闭孔隙进行冻融作用下孔隙壁应力计算,并分别提出了以下两种形状的封闭孔隙力学计算模型。
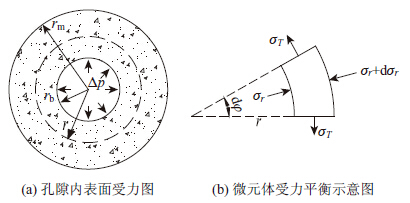
1.2.1 球形孔隙壁应力计算在进行球形封闭孔隙壁应力计算时做了以下假设[30]:(1)水泥砂浆为连续、弹性、均匀的各向同性体;(2)封闭孔隙是由一定厚度水泥砂浆围成的内径为rb,外径为rm的空心圆球,且忽略体力; (3)封闭孔隙水结冰产生的膨胀压力均匀作用在圆球内表面。如图 1(a)所示。
|
| 图 1 球形封闭孔受力计算模型 Fig. 1 Calculation model of sphere closed pore |
从水泥砂浆弹性体割取一个微小六面体,如图 1(b)所示。依据弹性力学球对称问题,对该六面体在径向列平衡方程并化简得:
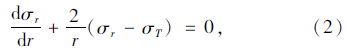
将球形封闭孔隙的几何方程代入物理方程,得到弹性方程:
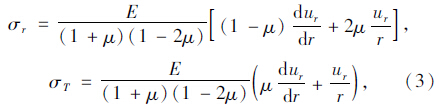
将式(3)代入式(2),化简得到按位移求解的封闭孔隙基本微分方程:
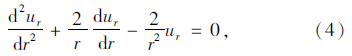

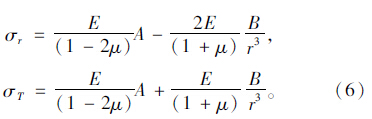
为求A,B,将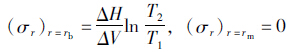 边界条件代入式(6)得:
边界条件代入式(6)得:
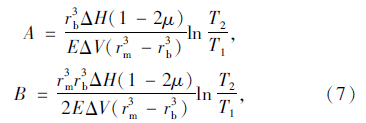
将A,B代入式(6)得到球形封闭孔隙孔壁拉应力σT为:
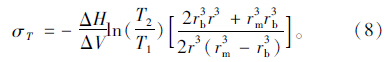
圆柱形封闭孔隙壁应力计算所采用的假设与前述球形封闭孔隙相同。孔隙水结冰产生的膨胀压力均匀作用在圆柱体内表面,如图 2(a)所示。
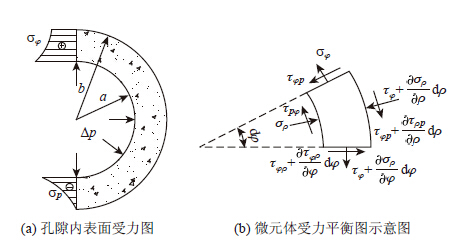
|
| 图 2 圆柱形封闭孔受力计算模型 Fig. 2 Calculation model of cylindrical closed pore |
从圆柱形孔隙横截面取一个微元体,如图 2(b)所示。应力呈轴对称分布,依据弹性力学知应力函数φ只是径向坐标ρ的函数,从而得其应力分量为:
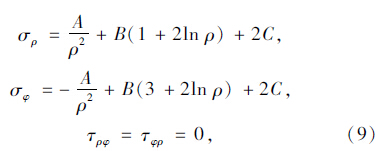
对于圆柱形封闭孔隙边界条件为:
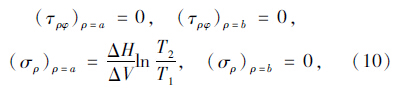
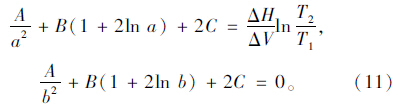
由于圆柱形孔隙的应力分布成轴对称分布,因而根据轴对称应力状态下的环向位移表达式知B=0,故式(11)可求解为:
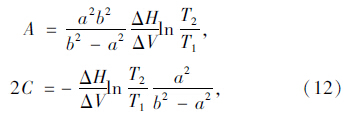
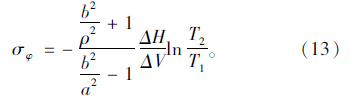
某种水泥砂浆的各项已知参数如下:
(1)水泥砂浆由水、水泥、矿物掺合料、砂组成,水为240 kg/m3,水泥为422 kg/m3,矿物掺合料为178 kg/m3,砂为1 364 kg/m3。其中矿物掺合料是按m(硅灰)∶m(粉煤灰)∶m(矿渣)=1∶6∶3配合而成,水泥砂浆水胶比为0.4,胶砂比为0.44,计算得此配合比下1 m3水泥砂浆中水泥石量p为0.48 m3。
(2)水泥砂浆气孔的比表面积α为14.84 mm-1,含气量试验测得水泥砂浆含气量A为3.5%。
(3)水由液相变到固相的体积变化ΔV为1.629×10-5m3/mol,摩尔相变焓ΔH为6×103 J/mol。
(4)水泥砂浆的养护温度t1为20 ℃,转化为绝对温度为T1=293.15 K,受冻温度t2为-20 ℃,转化为绝对温度为T2=253.15 K。
具体计算步骤如下:
(1)计算作用于封闭孔隙内表面的均布压应力ΔP
根据克拉贝龙方程,代入各参数得到作用于封闭孔隙内表面的均布压应力ΔP为:
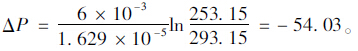
(2)计算封闭孔隙半径rb及气孔间距系数L
①球形封闭孔隙
假设水泥砂浆空间中均匀布置内径为rb的球体气孔,则一个球形气孔的体积V、表面积S分别为:
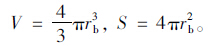
根据气孔比表面积α的计算公式rb=3/α可得:
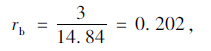
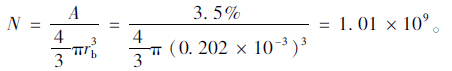
Power[2, 3, 4]认为气孔间距系数为水泥石中任一点和相邻任一气泡球面之间的最大距离。故对于封闭孔隙可以看成是等于把水泥石(包括气孔)分割成个数与气孔个数N相等的立方体,外径rm为其对角线的一半,即:
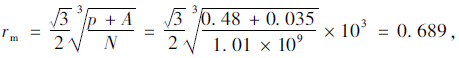
②圆柱形封闭孔隙
对于圆柱形封闭孔隙,假设水泥砂浆空间中均匀布置半径为a,高度为2a的圆柱形封闭孔隙,则一个圆柱形气孔的体积V、表面积S各为:
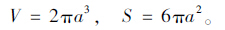
根据气孔比表面积α的计算公式a=2/α可得:
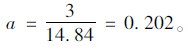
由此可得圆柱形封闭孔隙的个数N为:
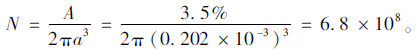
对于封闭孔隙外径b为:
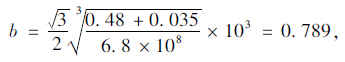
(3)计算封闭孔隙孔壁拉应力
①球形封闭孔隙
根据球形封闭孔隙孔壁拉应力式(8)计算得到孔壁内外表面拉应力为:
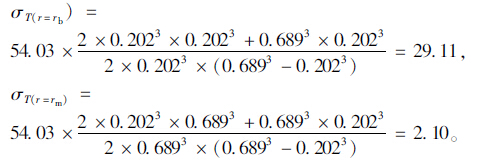
②圆柱形封闭孔隙
根据圆柱形封闭孔隙孔壁拉应力式(13)计算得到孔壁内外表面拉应力为:
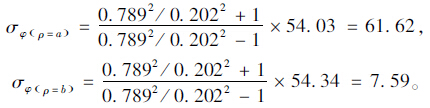
所以,按上述配合比设计的水泥砂浆,若浆体空间中封闭孔隙均匀布置,则经计算可得,在受冻温度为-20℃时,球形封闭孔隙内外表面产生的拉应力分别为29.11,2.10 MPa;圆柱形封闭孔隙内外表面产生的拉应力分别为61.62,7.59 MPa。
2 孔隙参数对孔壁应力影响分析为明确影响封闭孔隙孔壁应力参数的敏感性,本文对两种封闭孔隙孔壁拉应力计算参数进行讨论,来分析孔隙形状、半径、孔壁厚度、冻结温度对孔壁应力的影响程度。
2.1 冻结温度对封闭孔隙孔壁拉应力的影响假设封闭孔隙两种计算模型的内径均为 0.1 mm,按照上述气孔排列模式得到封闭孔隙的外径,由式(8)、(13)计算得到两种模型在不同受冻温度下的孔壁拉应力,计算结果如表 1所示。
| 受冻温度 | 球形孔/MPa | 圆柱形孔/MPa | |||
| 摄氏/℃ | 开氏/K | 内表面 | 外表面 | 内表面 | 外表面 |
| 0 | 273.15 | 14.02 | 1.01 | 29.68 | 3.66 |
| -10 | 263.15 | 21.43 | 1.54 | 45.35 | 5.59 |
| -20 | 253.15 | 29.11 | 2.10 | 61.62 | 7.59 |
| -30 | 243.15 | 37.11 | 2.67 | 78.56 | 9.68 |
| -40 | 233.15 | 45.45 | 3.27 | 96.20 | 11.85 |
从表中可以看出:
(1)内表面拉应力大于外表面拉应力,冻胀破坏微小裂缝在孔隙内表面首先形成,在一定条件下,这些裂缝将急剧扩展,从而导致内部结构产生冻胀破坏,且冻结温度越低,封闭孔隙孔壁所受拉应力越大。这是因为砂浆的受冻破坏主要是由气孔中的水结冰产生膨胀力造成的,温度越低,气孔中可冻水量越多,对孔壁产生的膨胀力越大,造成孔壁所受拉应力就越大。
(2)在受冻温度相同的条件下,球形与圆柱形孔隙受到的结冰压力相同,但是圆柱形封闭孔隙拉应力明显大于球形。这是由于孔隙结冰压力的大小只取决于受冻温度,而与孔隙的体积无关,在同样的结冰压力作用下,球形孔隙受力更加均匀的缘故。
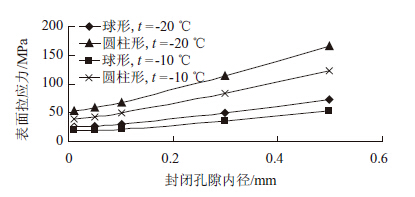
2.2 气孔内径对封闭孔隙孔壁拉应力的影响假设封闭孔隙两种计算模型的孔间距系数均为0.2 mm,且保持不变,封闭孔隙内径从0.01 mm变化到0.5 mm,分别计算两种模型在冻结温度为-20 ℃,-10 ℃时的孔隙内表面拉应力,不同孔隙内径下的孔隙内表面拉应力变化规律如图 3所示。
|
| 图 3 封闭孔隙内表面拉应力随孔隙内径变化规律 Fig. 3 Rule of tensile stress of inside surface of closed pore varying with pore diameter |
可以看出,两种计算模型的孔隙内表面拉应力都随着封闭孔隙内径的增大而增大,当受冻温度为-20 ℃,孔间距系数为0.2 mm,孔径从0.01 mm变化到0.5 mm时,球形孔隙和圆柱形孔隙孔壁内表面拉应力分别从27.03,54.28 MPa变化到73.49,166.6 MPa,当受冻温度为-10 ℃时,孔间距系数为0.2 mm,孔径从0.01 mm变化到0.5 mm 时,球形孔隙和圆柱形孔隙孔壁内表面拉应力分别从19.89,39.95 MPa变化到54.08,122.61 MPa,增大了63.22%,67.42%。这是由于孔径大小决定了孔隙中水的冰点,孔径越大,冰点越高,成冰率也越高,因而可冻水量也就越多,从而孔隙内部膨胀力越大,孔壁所受拉应力也就越大。
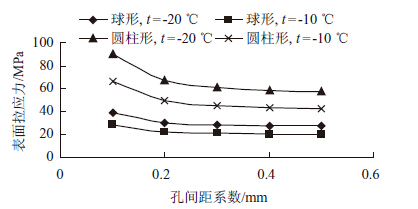
2.3 孔间距系数对封闭孔隙孔壁拉应力的影响假设封闭孔隙两种计算模型的空隙内径均为0.1 mm 且保持不变,封闭孔隙间距系数从0.1 mm增加到0.5 mm,分别计算两种模型在冻结温度为-20 ℃,-10 ℃时的孔隙内表面拉应力,不同孔间距系数下的孔隙内表面拉应力变化规律如图 4所示。
|
| 图 4 封闭孔隙内表面拉应力随孔间距系数变化规律 Fig. 4 Rule of tensile stress of inside surface of closed pore varying with pore spacing factor |
可以看出,两种计算模型的孔隙内表面拉应力都随着封闭孔隙孔间距系数的增大而减小,这与连通孔关于孔间距系数对冻胀力的影响趋势正好相反,当受冻温度为-20 ℃,孔径为0.1 mm,孔间距系数从0.1 mm变化到0.5 mm时,球形孔隙和圆柱形孔隙孔壁内表面拉应力分别从38.6,90.06 MPa变化到27.40,57.12 MPa;当受冻温度为-10 ℃时,孔径为0.1 mm,孔间距系数从0.1 mm变化到0.5 mm时,球形孔隙和圆柱形孔隙孔壁内表面拉应力分别从28.4,66.27 MPa变化到20.16,42.04 MPa,减小了29.0%,36.6%,且变化主要集中在孔间距系数为2倍孔径范围内。当孔间距系数超过孔径2倍时,变化趋于平缓,可近似认为相同。这是因为对于连通孔隙,当孔隙水结冰产生压力时,水能够从毛细管经过没有冰冻的孔扩散外逸至自由空间,缓解冻融过程中产生的冰胀压力和毛细孔水的渗透压力。若孔间距系数增大,则孔隙水迁移时所经历时间增长,孔道阻力增大而使孔隙水不易排出,从而使孔壁所受拉应力增大;而对于封闭孔隙,部分水结冰产生压力,由于孔隙是全封闭的,未冻结水不能向外迁移释放部分压力,因而当封闭孔隙孔壁越厚时,其所承受的拉应力也越小,但孔壁所受拉应力也并不是随孔壁厚度增大而无限减小的,这可以通过力学方程得到验证。
3 结 论本文运用热力学平衡原理和弹性力学理论,建立了封闭孔隙冻胀破坏力学计算模型,推导了孔壁应力的计算公式,并对影响孔壁应力的参数敏感性进行了分析,得到以下结论:
(1)推导的封闭孔隙孔壁应力计算公式包括球形、圆柱形两种孔隙形状的孔壁拉应力公式,并运用该公式对某一配合比水泥砂浆在受冻温度为-20 ℃ 时的孔壁拉应力进行计算,得到球形封闭孔隙内表面拉应力为圆柱形的47%,对抗冻性有利。
(2) 外界环境受冻温度对封闭孔隙孔壁拉应力影响最大,受冻温度越低,孔壁拉应力越大,当受冻温度从0 ℃降低到-40 ℃时,圆形及圆柱形孔径的封闭孔隙均会出现裂缝,遭到破坏;而对于水泥砂浆内部孔隙半径及孔间距系数而言,孔壁拉应力随着封闭孔隙内径的增大而增大,随着孔间距系数的增大而减小,当孔间距系数超过孔径2倍时,孔壁拉应力变化趋于平缓,可近似认为相同。
| [1] | 郭成举.混凝土冻害的机制[J].混凝土与水泥制品,1982 (3):9-19. GUO Cheng-ju. The Mechanism of Concrete Freezing Injury [J]. China Concrete and Cement Products,1982 (3): 9-19. |
| [2] | POWERS T C,HELMUTH R A. Theory of Volume Changs in Hardened Portland-cement Paste During Freezing[C]//Proceedings of the Thirty-second Annual Meeting of the Highway Research Board. Washington, D.C.:Transportation Research Board,1953: 285-297. |
| [3] | POWERS T C,WILLIS T F. The Air Requirement of Frost Resistant Concrete[C]//Proceedings of the Twenty-ninth Annual Meeting of the Highway Research Board. Washington, D.C.:Transportation Research Board,1950: 184-211. |
| [4] | POWERS T C. A Working Hypothesis for Further Studies of Frost Resistance of Concrete[J]. Journal of the American Concrete Institute,1945,41(4): 245-272. |
| [5] | SETZER M J. Basis of Testing the Freeze-thaw Resistance:Surface and Internal Deterioration[C]//Frost Resistance of Concrete. London:[s.n.] 1997: 157-173. |
| [6] | SETZER M J. Micro-ice-lens Formation in Porous Solid [J]. Journal of Colloid and Interface Science,2001,243(1):193-201. |
| [7] | SCHERER G W. Crystallization in Pores [J]. Cement and Concrete Research,1999,29(8): 1347-1358. |
| [8] | VALENZA II J J,SCHERER G W. A Review of Salt Scaling: II.Mechanisms [J]. Cement and Concrete Research, 2007,37(7): 1022-1034. |
| [9] | 刘西拉,唐光普. 现场环境下混凝土冻融耐久性预测方法研究[J]. 岩石力学与工程学报,2007,26(12):2412-2419. LIU Xi-la, TANG Guang-pu. Research on Prediction Method of Concrete Freeze-thaw Durability under Field Environments [J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(12): 2412-2419. |
| [10] | 蔡昊. 混凝土抗冻耐久性预测模型[D]. 北京:清华大学,1998. CAI Hao. Prediction Model of Concrete Freeze-thaw Durability [D]. Beijing: Tsinghua University,1998. |
| [11] | 商怀帅,欧进萍,宋玉普. 混凝土结构冻融损伤理论及冻融可靠度分析[J]. 工程力学,2011,28(1): 70-74. SHANG Huai-shuai,OU Jin-ping,SONG Yu-pu. Analysis on Reliability and Freeze-thaw Damage Theory of Concrete [J]. Engineering Mechanics,2011,28(1): 70-74. |
| [12] | 巩妮娜. 混凝土冻融破坏的有限元模拟研究[D]. 北京: 清华大学,2005. GONG Ni-na. Finite Element Analysis for Concrete Freeze-thaw Damage [D]. Beijing: Tsinghua University,2005. |
| [13] | 郭利霞,罗国杰,钟凌,等. 水工混凝土结构施工期冻融破坏仿真模拟[J]. 农业工程学报,2012,28(18):82-87. GUO Li-xia,LUO Guo-jie,ZHONG Ling,et al. Simulation Study on Freeze-thaw Damage of Hydraulic Concrete in Construction Period[J]. Transactions of the Chinese Society of Agricultural Engineering,2012,28(18): 82-87. |
| [14] | 覃丽坤,宋玉普,陈浩然,等. 双轴拉压混凝土在冻融循环后的力学性能及破坏准则[J]. 岩石力学与工程学报,2005,24(10): 1740-1745. QIN Li-kun,SONG Yu-pu,CHEN Hao-ran,et al. Mechanical Property and Failure Criterion of Concrete under Biaxial Tension and Compression after Freeze-thaw Cycles [J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(10): 1740-1745. |
| [15] | 张众,宋玉普,贾致荣. 冻融后普通混凝土双轴等效单轴应变本构模型试验研究[J]. 土木工程学报,2009,42(12): 105-111. ZHANG Zhong,SONG Yu-pu,JIA Zhi-rong. Experimental Study of Biaxial Equivalent Uniaxial Strain Constitutive Model for Ordinary Concrete after Freeze-thaw Cycling [J]. China Civil Engineering Journal,2009,42(12):105-111. |
| [16] | 冀晓东,宋玉普,刘建. 混凝土冻融损伤本构模型研究[J]. 计算力学学报,2011,28(3): 461-467. JI Xiao-dong, SONG Yu-pu, LIU Jian. Study on Frost Damage Constitutive Model of Concrete [J]. Chinese Journal of Computational Mechanics,2011,28(3): 461-467. |
| [17] | 商怀帅,杨鲁生. 基于损伤理论的混凝土双轴压本构模型[J]. 中南大学学报:自然科学版,2013,44(1): 340-344. SHANG Huai-shuai,YANG Lu-sheng. Constitutive Model of Damage of Concrete under Biaxial Compression [J]. Journal of Central South University:Science and Technology Edition,2013,44(1): 340-344. |
| [18] | 曹大富,富立志,杨忠伟,等. 冻融循环作用下混凝土受压本构特征研究[J]. 建筑材料学报,2013,16(1): 17-23. CAO Da-fu,FU Li-zhi,YANG Zhong-wei,et al. Study on Constitutive Relations of Compressed Concrete Subjected to Action of Freezing-Thawing Cycles[J]. Journal of Building Materials,2013,16(1): 17-23. |
| [19] | 廉惠珍,童良,陈恩义. 建筑材料物相研究基础[M]. 北京:清华大学出版社,1996. LIAN Hui-zhen,TONG Liang, CHEN En-yi. Research Basis of the Phase of Building Materials [M]. Beijing: Publishing House of Tsinghua University,1996. |
| [20] | MEHTA P K, BURROWS R W. Building Durable Structures in the 21st Century [J]. Concrete International,2001,23(3): 57-63. |
| [21] | SHAH S P,WANG K,WEISS W J. Mixture Proportioning for Durable Concrete: Challenges and Changes [J]. Concrete International,2000,22(9): 73-78. |
| [22] | 于雪梅,唐立强,王堃. 内压作用下球形孔洞膨胀损伤力学分析[J]. 哈尔滨工程大学学报, 2010, 31(8): 1034-1038. YU Xue-mei,TANG Li-qiang,WANG Kun. Simulating the Mechanics of Damage to Geological Materials with Spherical Cavity Explosions under Internal Pressure [J]. Journal of Harbin Engineering University,2010,31(8): 1034-1038. |
| [23] | 于雪梅. 岩土材料中球形孔洞膨胀问题的力学分析[D]. 哈尔滨: 哈尔滨工程大学,2010. YU Xue-mei. Mechanical Analysis on Spherical Cavity Expansion Problem in Geomaterials[D]. Harbin: Harbin Engineering University,2010. |
| [24] | 吴国辉,王勇,邹广平,等. 理想弹塑性压力敏感性材料中球形孔洞的动态扩展研究[J]. 应用力学学报,2012,29(5): 508-511. WU Guo-hui,WANG Yong,ZOU Guang-ping,et al. Dynamic Expansion of the Spherical Cavity in the Elastic Perfectly-Plastic Pressure Sensitive Material [J]. Chinese Journal of Applied Mechanics,2012,29(5): 508-511. |
| [25] | 吴中伟,廉惠珍. 高性能混凝土[M]. 北京: 中国铁道出版社,1999. WU Zhong-wei,LIAN Hui-zhen. High Performance Concrete [M]. Beijing: China Railway Publishing House,1999. |
| [26] | 张士萍,邓敏,唐明述. 混凝土冻融循环破坏研究进展[J]. 材料科学与工程学报,2008,26(6): 990-994. ZHANG Shi-ping,DENG Min,TANG Ming-shu. Advance in Research on Damagement of Concrete Due to Freeze-thaw Cycles[J]. Journal of Materials Science and Engineering,2008,26(6): 990-994. |
| [27] | 李天瑗.试论混凝土冻害机理—静水压与渗透压的作用[J].混凝土与水泥制品, 1989, (5): 8-11. LI Tian-yuan. Try to Discuss the Mechanism of Concrete Freezing Injury: The Role of Hydrostatic Pressure and Osmotic Pressure [J]. China Concrete and Cement Products,1989,(5): 8-11. |
| [28] | 崔黎丽,刘毅敏. 物理化学[M]. 北京:科学出版社,2011. CUI Li-li,LIU Yi-min. Physical Chemistry [M]. Beijing: Science Press,2011. |
| [29] | ZHOU Z Y,MIHASHI H. Micromechanics Model to Describe Strain Behavior of Concrete in Freezing Process [J]. Journal of Materials in Civil Engineering,2008,20(1):46-53. |
| [30] | 徐芝纶. 弹性力学[M]. 北京:高等教育出版社,2006. XU Zhi-lun. Elasticity [M]. Beijing: Higher Education Press,2006. |
 2015, Vol. 31
2015, Vol. 31

 ,
,