扩展功能
文章信息
- 邵俊虎, 赵人达, 徐腾飞
- SHAO Jun-hu, ZHAO Ren-da, XU Teng-fei
- 计入动力风荷载的船舶撞击桥梁动力响应研究
- Research on Dynamic Response of Ship-bridge Collision Considering Dynamic Wind Load
- 公路交通科技, 2015, Vol. 31 (4): 70-77
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 70-77
- 10.3969/j.issn.1002-0268.2015.04.013
-
文章历史
- 收稿日期:2014-04-25
随着桥梁建设发展和通航船舶增多,船撞桥问题日益突出,解决船撞问题的关键技术之一是计算碰撞过程中桥梁结构的响应。已有许多学者对此类问题进行了研究。计算方法主要有以下几种:(1)通过经验公式估算等效船撞力,再根据静力学理论计算结构响应;(2)基于有限元的船桥耦合算法计算船撞力以及桥梁结构的动力响应;(3)基于有限元的碰撞-接触算法方法确定桥梁结构响应。碰撞-接触算法计算结果比较精确,但对计算条件要求较高,难以广泛应用,等效船撞力无法对计入动力响应,导致计算结果失真,而碰撞耦合算法可以兼顾效率和精度,近年来得到了广泛应用。Heins-Derucher[1]最先提出了船舶与桥梁耦合分析的计算方法。随后美国Kentucky大学Harik[2]教授等人推导了驳船与桥墩碰撞函数。Cowan[3]提出了船桥碰撞耦合解法,其基本思路是将撞击船舶的运动用撞击方向的单自由度来描述,桥墩结构用一个多自由度体系模拟,二者之间根据相对位移大小通过非线性的力和变形关系(船头等效刚度)耦合起来,并通过迭代求解得到船撞力和桥梁响应。Yuan[4]将船撞耦合碰撞算法引入到多驳船与桥墩碰撞计算中,成功地对碰撞过程进行了模拟,并验证了这种算法的正确性和高效性。Hendrix[5]和Zhang[6]等人对船桥耦合方法进行了研究,结果表明该方法具有良好的求解效率和精度。Fan[7]对Cowan的提出的拟静力船头刚度进行了修正,并采用船桥耦合分析算法计算了一座斜拉桥在船舶碰撞下的动力响应。
对于船桥耦合分析算法,船头等效刚度的确定直接影响到分析结果的准确性。船头等效刚度的确定方法主要有两类,第一类是通过试验获得数据,并经过处理后得出船头等效刚度模型,如Meier-Drnberg在1983年以欧洲-IIa型船舶船头为研究对象,对船舶撞击过程进行了3次试验研究[8],得出了船舶撞击变形、船舶撞击力之间的相互关系;另外一类是通过接触碰撞分析得出船头等效刚度模型,如Cowan[3]、樊伟[7]、王君杰[9, 10]都采用这类方法对船头等效刚度做了研究。
随着航运的发展,通航船舶的吨位和密度越来越大,船舶的抗风等级也随之增加,大风天气下桥区船舶也时有通行,这增大了船舶撞击桥梁的几率和危险性。对于船舶撞击桥梁,往往单独计算撞击效应,再和静风荷载进行组合,而实际上,动力风荷载和船撞荷载表现为耦合作用。本文首先对船桥耦合分析算法进行研究,采用C++语言编制了计算分析程序,并提出基于接触碰撞分析的船头刚度构建方法,最后运用该方法计算不同等级风荷载作用下,船舶撞击桥梁的动力响应,探讨风荷载对船舶撞击力以及桥梁结构响应的规律,得出了一些有益的结论。
1 船桥耦合分析模型 1.1 改进的船舶运动方程求解方法本文基于以下几个假定建立了船舶的运动方程:
(1)船舶与桥梁撞击过程中,沿撞击方向的船撞力对桥梁结构起主要作用,将船舶假设为一个沿撞击方向运动的单自由度体系。
(2)不考虑船舶船头的阻尼影响。
(3)对于其他作用于船舶上的动力荷载,只考虑在船舶运动方向上的分量。
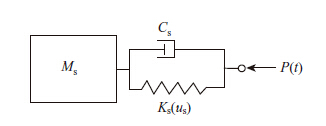
根据以上假设,可得出船舶动力模型,见图 1。根据D′Alembert原理,船舶运动方程为:
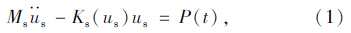
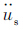 为船舶加速度;us为船舶与桥梁间的相对位移;P(t)为作用于船舶上动力荷载的合力,可为撞击力、风荷载、波浪荷载等动力荷载。
为船舶加速度;us为船舶与桥梁间的相对位移;P(t)为作用于船舶上动力荷载的合力,可为撞击力、风荷载、波浪荷载等动力荷载。
|
| 图 1 船舶动力模型 Fig. 1 Dynamic model of ship |
对于式(1)可采用数值方法求解,文献[3]采用中心差分法对其进行数值求解,但中心差分法收敛性取决于时间步的大小。本文采用Newmark-β方法对船舶动力方程进行求解,当积分常数取值合理时,为无条件收敛,更加适合动力方程的求解。
由文献[11]可知,Newmark-β法的两个基本公式为:
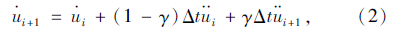
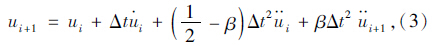
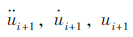 分别为本时刻船舶加速度、速度、位移;
分别为本时刻船舶加速度、速度、位移;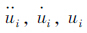 分别为上一时刻船舶加速度、速度、位移;γ,β分别为积分常数,为保证无条件收敛,一般取β=0.25,γ=0.5。
分别为上一时刻船舶加速度、速度、位移;γ,β分别为积分常数,为保证无条件收敛,一般取β=0.25,γ=0.5。对于式(1)所示的单自由度系统,可得出ti+1时刻船舶的加速度:

将式(4)代入式(2)、(3)中,再结合ti时刻船舶的加速度、速度以及位移,可以得出ti+1时刻的速度和位移。对ti+1作用于船舶结构上的桥梁与船舶之间的耦合撞击力需经过迭代求解。
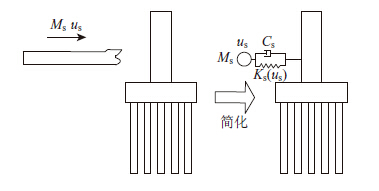
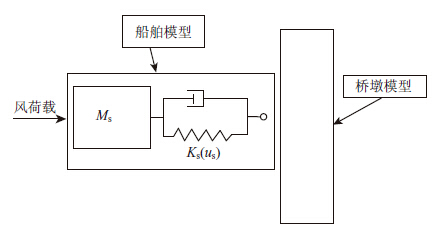
1.2 基于船桥耦合分析流程将整个船桥系统简化为如图 2所示的模型,船舶模型可简化为集中质量、非线性弹簧和阻尼器,其中集中质量表示船舶质量,非线性弹簧模拟船头等效刚度,阻尼器为船头结构阻尼,桥梁模型采用有限元方法进行离散。船舶与桥梁之间碰撞产生的碰撞力对于桥梁和船舶来说,为作用力与反作用力的关系,每一时刻平衡力的求解需经过迭代得出。
|
| 图 2 船桥系统模型图 Fig. 2 Model of ship-bridge system |
船撞耦合分析的迭代过程如下[3]:
(1)指定初始条件下,桥梁和船舶的初始位移、速度、加速度。
(2)假设ti+1时刻第h次迭代时桥梁撞击点处位移、速度、加速度,当h=1时为ti时刻位移、速度、加速度,即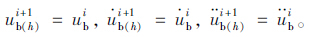
(3)迭代计算ti+1时刻船舶的位移usi+1、速度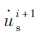 、加速度
、加速度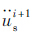 、 船桥碰撞力pci+1,过程如下:
(a)假设船舶ti+1时刻的第k次迭代船桥碰撞力,当k=1时,
、 船桥碰撞力pci+1,过程如下:
(a)假设船舶ti+1时刻的第k次迭代船桥碰撞力,当k=1时,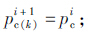 当k≠1时,
当k≠1时,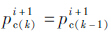 。
(b)根据式(4)计算ti+1时刻船舶加速度us(k)i+1。
(c)根据式(2)、(3)计算船舶位移和速度。
(d)计算ti+1时刻船舶和桥梁碰撞点处的相对位移uri+1=
。
(b)根据式(4)计算ti+1时刻船舶加速度us(k)i+1。
(c)根据式(2)、(3)计算船舶位移和速度。
(d)计算ti+1时刻船舶和桥梁碰撞点处的相对位移uri+1=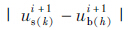 。
(e)根据等效船头刚度模型求解k+1次船桥碰撞力:
。
(e)根据等效船头刚度模型求解k+1次船桥碰撞力: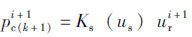 ,则两次计算的船撞力误差为:
,则两次计算的船撞力误差为: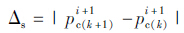 。
(f)如果Δs小于规定迭代误差,则迭代完毕;如果大于规定的迭代误差,则令
。
(f)如果Δs小于规定迭代误差,则迭代完毕;如果大于规定的迭代误差,则令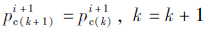 ,重新转入第(b)步进行迭代计算,直至船桥碰撞力收敛。
,重新转入第(b)步进行迭代计算,直至船桥碰撞力收敛。
(4)根据有限元方法计算桥梁结构ti+1时刻第h+1次迭代的位移、速度、加速度。
(5)比较两次计算的桥梁位移误差Δb=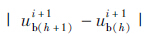 。如果Δb小于规定迭代误差,则迭代完毕,转入第(6)步;如果大于规定的迭代误差,则
。如果Δb小于规定迭代误差,则迭代完毕,转入第(6)步;如果大于规定的迭代误差,则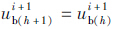 ,令h=h+1,转入第(3)步进行迭代计算。
,令h=h+1,转入第(3)步进行迭代计算。
(6)判断是否所有荷载步计算完毕;如果是,则求解完毕;如果否,则转入第(2)步继续求解。
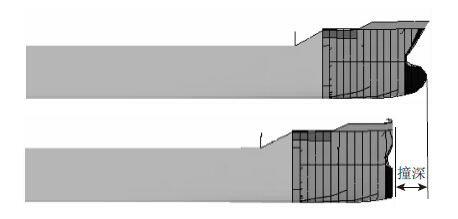
1.3 基于接触碰撞分析的船头等效刚度构建方法对于船舶刚度的构建,多根据接触碰撞分析获取船桥碰撞力时程和船头撞深时程(见图 3),然后以时间变量为中间量进行换算,最终得到船头等效刚度。而船桥耦合分析模型和接触碰撞分析模型最大的区别在于前者采用了单自由度模型来模拟船舶,而后者采用多自由度模型来模拟。从能量和动量的角度来看,两种模型很难保证在同一时刻碰撞力大小吻合良好的同时,最大撞深、撞击持续时间也吻合良好。为此,本文提出了一种构建等效船头刚度方法,旨在令两种模型在最大撞深、撞击持续时间吻合良好的同时,保证撞击力时程趋势大致相同。
|
| 图 3 船头撞深 Fig. 3 Collision depth of ship bow |
提出的方法基于以下假设:(1)由于桥墩刚度一般远大于船头刚度,船舶动能全部转换为船头变形产生的变形能;(2)忽略碰撞过程中桥梁局部塑性变形耗散的能量;(3)微小时间段内,碰撞力与变形关系为线性关系。
对于船舶和桥梁碰撞系统,满足能量守恒原理和动量守恒定理:
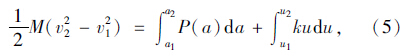
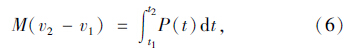
则船头刚度构建步骤如下:
(1)根据实际情况,建立船舶和桥梁的有限元模型进行接触碰撞分析。根据假设(1),可采用刚性墙代替桥梁结构,但需要注意的是刚性墙的截面尺寸需和碰撞区域桥梁结构尺寸一致。
(2)提取船舶撞击桥梁的撞击力时程曲线。
(3)结合撞击力时程曲线,根据式(6)计算每一时间段内动量增量以及对应的速度增量Δvt,将所有求得的速度增量进行累加,可得到所有时刻的速度;
(4)根据所有时间段对应的动能减少量,结合假设(1)、(3)和式(5),可以得出所有时间段内的船头变形增量;
(5)将步骤(4)得出的船头变形增量进行累加得到船头在所有时刻总变形;
(6)设船舶初始速度为v0,船舶撞击力卸载时刻对应的船舶速度为vB,判断是否满足|vB-ε|=0,其中ε为一较小量。如果不满足,则转入第(7)步;如果满足,则计算结束,以时刻为中间变量,换算出等效船头刚度曲线;
(7)根据式(7)计算每时刻速度分配系数:
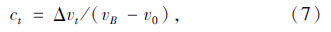
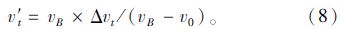
根据式(6)计算每时刻分配荷载F′,则新的船撞力FN=F+F′,式中F为上步计算的船撞力,完毕后转入第(3)步继续计算。
需要说明的是,本文方法在构建船头等效刚度的过程中使用了碰撞接触算法,而且所构建的等效刚度模型也只针对于本文工况,从这个角度看,直接使用碰撞接触算法无疑更加方便。但从统计的角度看,通航船舶存在一定数量的代表船舶,此外船舶航行速度也具有一定统计规律,根据不同的代表船舶和航行速度,结合本文方法,可建立一系列等效船头刚度,随着数据的增加,可较高效率地计算船舶撞击桥梁的动力响应,所以本文建议的方法具有一定的实际应用意义。
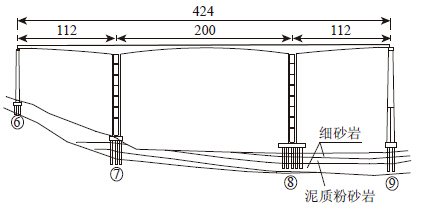
2 实际工程分析 2.1 工程概况忠县长江大桥主引桥为连续刚构,其上部结构为三跨(112+200+112)m预应力混凝土结构,全长424.00 m。箱梁顶板宽11.8 m,底板宽6.6 m。箱梁跨中及边跨现浇段高4.0 m,墩顶0号段高11.5 m,箱梁高度和底板厚度从中跨合龙段中心到悬臂根部按1.5次抛物线变化。主墩为10.0 m×6.6 m矩形空心墩,7号桥墩墩高102.00 m,8号桥墩墩高110.276 m。7号桥墩承台平面尺寸为15.0×25.0 m,高5.0 m;8号桥墩承台平面尺寸为直径D=25.0 m,高6.0 m;承台下布置14根桩,直径为2.5 m,均为嵌岩桩。桥梁的总体布置见图 3。
桥区最高通航水位为174.7 m,通航标准为I-(2)级,通航条件较好时可通航万吨级船队。三峡蓄水后,水位可保持在175 m左右,通航船舶吨位、密度都较大。
|
| 图 4 桥梁总体布置图(单位:m) Fig. 4 General layout of bridge(unit:m) |
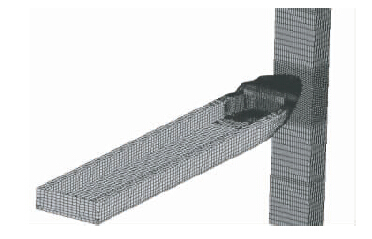
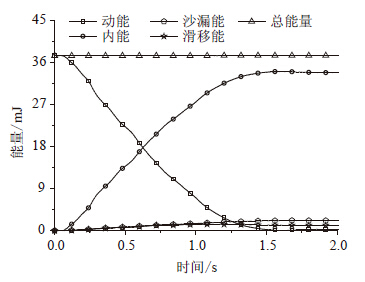
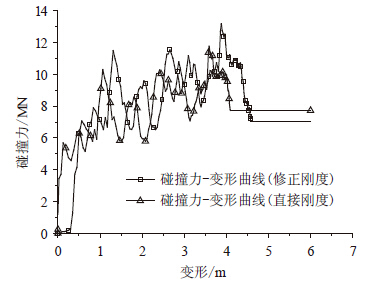
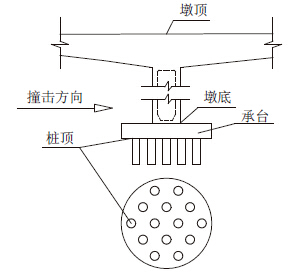
为验证程序的正确性,以本节连续刚构为工程背景,建立了3 000 t船舶以5 m/s的速度撞击8号桥墩的船舶和桥梁模型,对船舶正撞桥墩进行了接触碰撞有限元计算,船桥碰撞有限元模型见图 5,碰撞过程中的能量变化见图 6。由图中可见,船舶初始动能大部分转化为船桥系统内能,有少部分能量转化为了船舶与桥梁接触产生的滑移能,而沙漏能也得到了较好的控制。根据高精度碰撞有限元分析结果,采用1.3节方法得出了船头刚度曲线,见图 7。根据不同船头等效刚度确定方法确定的刚度进行船撞响应计算,由于8号墩为船舶撞击墩,重点关注8号墩位移和内力响应,位移和内力提取点见图 8,计算结果见图 9~图 12。为表示区别,本文方法确定的刚度称为修正刚度,采用撞深-船撞力确定的刚度称为直接刚度。
|
| 图 5 接触碰撞有限元模型 Fig. 5 Contact collision finite element mode |
|
| 图 6 能量变化 Fig. 6 Energy change |
|
| 图 7 等效船头刚度 Fig. 7 Equivalent stiffness of ship bow |
|
| 图 8 8号墩位移及内力提取点 Fig. 8 Extraction point of displacement and internal force of pier No.8 |
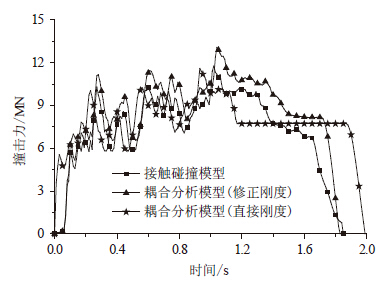
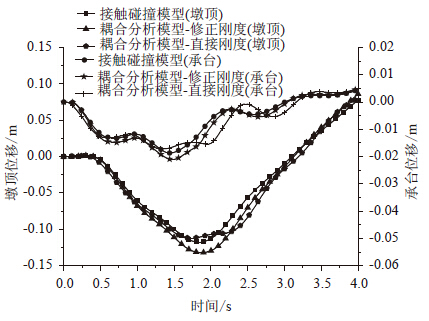
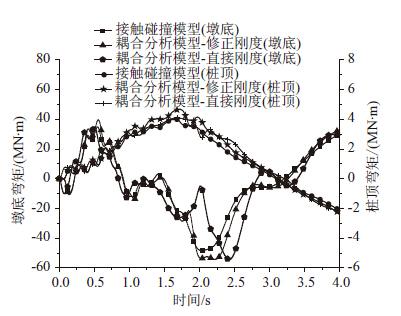
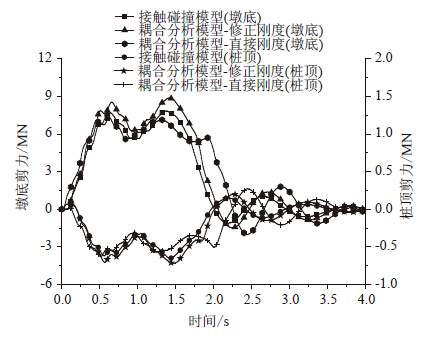
由图 9看以看出,修正刚度得出的船撞力与接触碰撞分析结果趋势基本是一致的,数值上略大,而直接刚度计算得出的船撞力峰值与接触碰撞算法结果大致相同,但在时间上有所延后,其碰撞时间也比较长。由图 10~图 12可以看出,在响应量的数值上,修正刚度计算的结果要好于采用直接刚度计算结果,但大于接触碰撞有限元计算结果,出现这种情况的原因是船桥耦合分析方法将船舶简化为一个单自由度结构,而接触碰撞有限元将船舶视为一个多自由度结构,后者在动能与内能之间的转换更加复杂,两种模型无法做到完全等效。此外船桥耦合分析方法无法考虑滑移能和沙漏能等,也导致了结构响应过大。但是,船桥耦合分析结果偏于安全,可为工程实际应用所接受。
|
| 图 9 撞击力 Fig. 9 Collision force |
|
| 图 10 8号墩顶和承台顶横桥向位移 Fig. 10 Lateral displacements of top and pile cap top of pier No.8 |
|
| 图 11 8号墩底和桩顶横桥向弯矩 Fig. 11 Lateral moments of bottom and pile top of pier No.8 |
|
| 图 12 8号墩底和桩顶横桥向剪力 Fig. 12 Lateral shears of bottom and pile top of pier No.8 |
为了探讨风荷载对桥梁船撞耦合分析结果的影响,本文根据桥址处实际情况,取10 m高处平均风速分别为10,15 m/s和20 m/s的3种工况,对船舶撞击桥梁的全过程进行了计算分析,其船头等效刚度仍采用图 7中的刚度。采用Kaimal谱和Davenport相关函数形式,基于谱解法模拟了主梁和主墩的横向脉动风速。
对于作用于船舶上的风荷载,其作用方向可分解为纵向和横向风荷载,根据1.1节中的假设(1),暂不考虑横向风荷载,其纵向风荷载受力图示见图 13。根据《港口工程荷载规范》[12]估算作用于船舶纵向的平均风荷载为40.5 kN,而根据图 9可知,最大船撞力为13 MN,相比船舶撞击力来说,船舶上作用风荷载可忽略不计。
|
| 图 13 风荷载作用示意图 Fig. 13 Schematic diagram of wind load |
本文基于C++语言编制船撞耦合分析程序,并提出了基于碰撞接触分析的船头刚度构建方法。
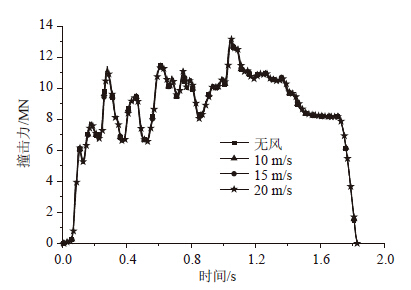
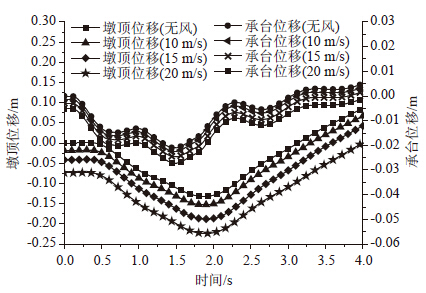
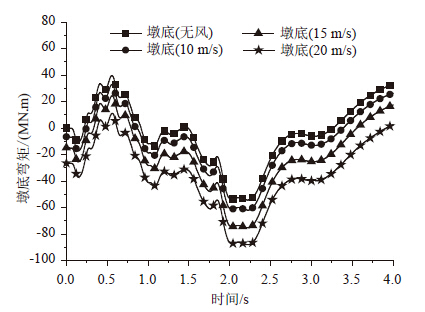
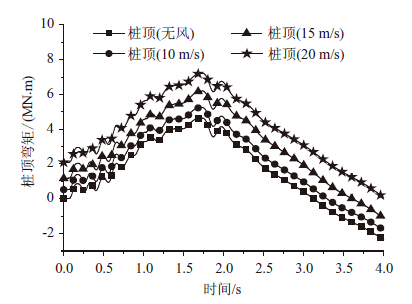
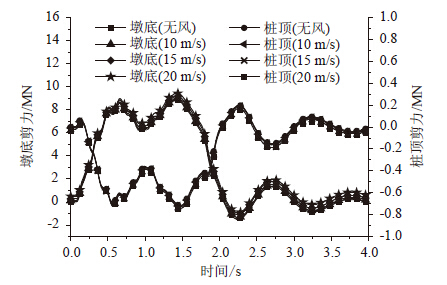
由图 14可以看出,风荷载对于船舶撞击力的影响较小,不同风荷载作用下,船撞力变化并不显著。由前述迭代计算流程可知,船撞力主要通过船舶和桥梁相对位移迭代得出,而风荷载对撞击点产生的位移很小,相比之下,船头变形量最大可到4~6 m,故风荷载产生的结构位移对船桥相对位移的贡献基本可以忽略,这个原因导致了风荷载不能显著影响船舶撞击力的大小。图 15给出了8号墩顶位移和承台位移;图 16~图 17给出了8号墩底和桩顶弯矩;图 18给出了8号墩底和桩顶剪力。由图可知,相比不考虑风荷载,风荷载对桥梁位移和弯矩均产生了较大的影响。表 1给出了不同工况下最大响应值,表 2给出了不同风速计算结果相对无风工况下的百分比。由表 2可知,墩顶位移和墩底内力响应增幅较大,墩顶位移增加最大比例为69.8%,墩底弯矩增加最大比例为62.1%;而对剪力影响较小,墩底剪力增加最大比例为6.6%。通过分析表明,虽然风荷载不能影响船舶撞击力大小,而当风荷载较大时,直接作用于结构上的风荷载对结构的响应增大起了主要作用,有必要考虑动力风荷载与船舶撞击力的共同作用。此外,脉动风对桥梁的作用并没有与船舶撞击作用发生耦合作用,考虑到实际应用的方便,脉动风作用可等效为静力作用进行分析。
|
| 图 14 撞击力 Fig. 14 Collision force |
|
| 图 15 8号墩顶和承台顶横桥向位移 Fig. 15 Lateral displacements top and pile cap top of pier No.8 |
|
| 图 16 8号墩底横桥向弯矩 Fig. 16 Lateral moments of bottom of pier No.8 |
|
| 图 17 8号桩顶横桥向弯矩 Fig. 17 Lateral moments of top of pier No.8 |
|
| 图 18 8号墩底和桩顶横桥向剪力 Fig. 18 Lateral shears of bottom and pile top of pier No.8 |
|
工况/ (m·s-1) | 位移/m | 弯矩/(MN·m) | 剪力/MN | |||
| 墩顶 | 承台 | 墩底 | 桩顶 | 墩底 | 桩顶 | |
| 无风 | -0.132 | -0.021 | -54.30 | 4.65 | 8.87 | -0.72 |
| 10 | -0.153 | -0.022 | -61.87 | 5.25 | 9.00 | -0.73 |
| 15 | -0.188 | -0.025 | -75.25 | 6.20 | 9.20 | -0.74 |
| 20 | -0.224 | -0.027 | -88.00 | 7.22 | 9.45 | -0.76 |
|
工况/ (m·s-1) | 位移/% | 弯矩/% | 剪力/% | |||
| 墩顶 | 承台 | 墩底 | 桩顶 | 墩底 | 桩顶 | |
| 10 | 16 | 6.8 | 14 | 12.9 | 1.5 | 1.3 |
| 15 | 42.9 | 17.1 | 38.6 | 33.4 | 3.8 | 3.3 |
| 20 | 69.8 | 29.2 | 62.1 | 55.3 | 6.6 | 5.6 |
| 注:表中数据为相对无风工况计算百分比 | ||||||
通过对一座连续刚构船舶撞击分析,得出了以下结论:
(1)分别采用本文方法与撞深-船撞力关系得出两种不同的等效船头刚度,并进行了船桥耦合计算,结果表明本文方法构建的船头等效刚度要优于撞深-船撞力关系构建的船头等效刚度,前者计算结果与接触碰撞计算结果吻合较好,峰值略大,但可应用于实际工程。
(2)通过对风荷载作用下船撞响应进行了计算,结果表明,风荷载对船撞力影响较小,但对桥梁响应影响较大,墩顶位移增加最大比例为69.8%,墩顶弯矩增加最大比例为62.1%;而对剪力影响较小,墩底剪力增加最大比例为6.6%。
(3)本文提出的刚度模型构建方法虽然能较好地确定船撞等效刚度,但不同船舶其船头刚度也不同,为满足计算需要,需通过大量接触碰撞分析建立不同情况下船头等效刚度库。
| [1] | DERUCHER K N. Analysis of Concrete Bridge Piers for Vessel Impact[C]//Proceedings of Sino-American Symposium on Bridge and Structural Engineering. Beijing:American Society of Civil Engineers (ASCE) and China Civil Engineering Society, 1982. |
| [2] | WHITNEY M W, HARIK I E, GRIFFIN J J, et al. Barge Collision Design of Highway Bridges[J]. Journal of Bridge Engineering,1996,1(2):47-58. |
| [3] | CONSOLAZIO G R, COWAN D R. Numerically Efficient Dynamic Analysis of Barge Collisions with Bridge Piers[J]. Journal of Structural Engineering, 2005, 131(8):1256-1266. |
| [4] | YUAN Peng, HARIK I E. One-dimensional Model for Multi-Barge Flotillas Impacting Bridge Piers[J]. Computer-aided Civil and Infrastructure Engineering,2008, 23(6):437-447. |
| [5] | HENDRIX J L. Dynamic Analysis Techniques for Quantifying Bridge Pier Response to Barge Impacting Loads[D]. Gainesville: University of Florida, 2003. |
| [6] | ZHANG Bi-bo. Influence of Pier Nonlinear, Impact Angle and Column Shape on Pier Response to Barge Impact Loading[D]. Gainesville: University of Florida, 2004. |
| [7] | FAN Wei, YUAN Wan-cheng, YANG Zhi,et al. Dynamic Demand of Bridge Structure Subjected to Vessel Impact Using Simplified Interaction Model[J]. |
| [8] | MEIER-DRNBERG K E. Ship Collisions, Safety Zones, and Loading Assumptions for Structures in Inland Waterways[R]. Duesseldorf, Germany: Association of German Engineer, 1983. |
| [9] | 孟德巍, 王君杰. 船艏正撞刚性墙力-撞深关系的简化公式研究[J].防灾减灾工程学报,2011,31(2): 160-165. MENG De-wei, WANG Jun-jie. Study on Simplified Formulae for Impact Force-Indentation Relationship under Frontal Impact of Ship-Bow to Rigid Wall [J]. Journal of Disaster Prevention and Mitigation Engineering,2011,31(2): 160-165. |
| [10] | 王君杰,卜令涛,金允龙,等.基于统计分析的撞击力-时间和撞击力-撞深概率模型[C]//第一届桥梁船撞学术研讨会论文集. 重庆:招商局重庆交通科研设计院有限公司,2011:217-229. WANG Jun-jie, BU Ling-tao, JIN Yun-long, et al. Force-time and Force-displacement Probability Models Based on Statistic Analysis[C]//Research and Engineering Application of Bridges Against Vessel Impact. Chongqing: China Merchants Chongqing Communications Research & Design Institute Co.,Ltd., 2011:217-229. |
| [11] | CLOUGH R W, PENZIEN J. Dynamics of Structures [M]. New York: McGraw Hill Inc., 1993. |
| [12] | JTS144—1—2010,港口工程荷载规范[S]. JTS144—1—2010, Load Code for Harbour Engineering [S]. |
| [13] | JTG D63—2007,公路桥涵地基与基础设计规范[S]. JTG D63—2007, Code for Design of Ground Base and Foundation of Highway Bridges and Culverts [S]. |
 2015, Vol. 31
2015, Vol. 31

 ,
,