扩展功能
文章信息
- 王强, 苏成
- WANG Qiang, SU Cheng
- 公路桥梁随机车流的平稳性和各态历经性检验
- Examination of Stationary and Ergodicity of Stochastic Traffic Flow on Highway Bridge
- 公路交通科技, 2015, Vol. 31 (4): 64-69
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 64-69
- 10.3969/j.issn.1002-0268.2015.04.012
-
文章历史
- 收稿日期:2014-05-05
2. 广东华路交通科技有限公司, 广东 广州 510420
2. Guangdong Hualu Transport Technology Co., Ltd., Guangzhou Guangdong 510420, China
由于公路桥梁上的车辆具有很强的随机性,进行汽车车辆与路桥结构相互作用研究时,对车辆的随机作用主要有两种方法,分别为以路面不平整度作为车辆随机激励的基本输入和以车辆随机轮轴特征作为车辆随机作用的基本输入。
以路面不平整度作为随机激励输入,研究路面随机不平整的自谱或互谱参数,寻求路面不平整度的特点和规律,以路面不平整度、激振频率、波长及波数谱密度等路面参数,运用随机振动理论建立车辆与结构相互作用的振动方程,作为车辆、路面和桥梁结构物动力响应研究的基础[1]。该方法多在车桥耦合系统动力学等理论领域应用较多[2],属于路面桥梁的动力学范畴。
以车辆随机轮轴特征作为车辆对路桥结构物随机作用的输入,用车辆轮轴重量、间距和前后车的间距等参数的调查统计结果进行随机模拟,以建立随机作用的模型[3, 4, 5, 6]。该方法属于桥梁静力学范畴。近年来随着对车辆调查能力的不断提高,如车辆动态称重(WIM)系统的出现[7]等,所获得的车辆信息不断丰富,对车辆随机特征的研究也不断深入,成为桥梁结构随机荷载研究的基本方法。
诚然,建立车辆随机作用模型需要对实际公路上的车辆进行实地调查统计,才能得到车辆的随机特征参数。而这些调查工作的历时有长有短,即使是长达几个月乃至几年的调查历时,其相对于桥梁的寿命期仍是短暂的。那么,这些调查统计的结果是否具有代表性?能否真实反映桥梁寿命期内所经历的荷载特征?这需要用随机过程理论来回答。本文由6条公路上共28条车道的实际车辆调查结果,分别构建得到各车道上的随机车流类型过程,以随机过程理论的重要数字特征——平稳性和各态历经性入手,研究公路桥梁上车辆的随机特征及其调查统计结果的统计代表性,为桥梁车流的随机分析提供依据。
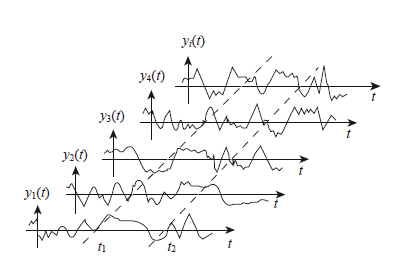
1 随机过程及其数字特征 1.1 随机过程的基本概念[8]由随机过程理论,如果作为随机试验或观测结果的随机变量Y(t)是时间T的函数,则称在时间T内的试验或观测结果为随机过程,用{Y(t),t∈T}表示,如图 1所示。{Y(t)}为观测结果所有可能取值的集合,为图 1中所有样本函数yi(t)的集合,称为状态空间。在t=t1时刻,Y(t1)是一个随机变量,为各yi(t1)在此时刻的可能取值。
|
| 图 1 随机过程示意图 Fig. 1 Schematic diagram of stochastic process |
对随机过程{Y(t),t∈T},定义在t=t1时刻随机变量Y(t1)的均值μY(t1)为各yi(t1)可能取值的平均值,即:
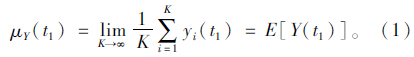
改变时刻t便可由式(1)得到所有样本函数在各个t时刻的函数值平均μY(t),称为集合均值,它反映随机过程{Y(t)}在各个时刻的摆动中心。
集合相关函数RY(t1,t2)描述的是随机过程在t1和t2=t1+τ两个不同时刻其状态之间的联系情况,用随机变量的乘积
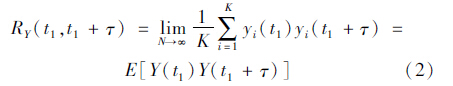
同样,改变时刻t可由式(2)得到所有样本函数在t和t+τ时刻两随机变量乘积的平均。
如果集合均值μY(t)在摆动中心附近的摆动幅度很小,且集合相关函数RY(t,t+τ)仅与τ有关而与时间起点t无关,即:
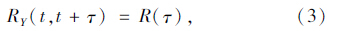
定义随机过程{Y(t),t∈T}的时间均值〈Y(t)〉为:
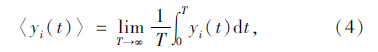
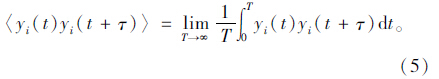
若随机过程的时间均值〈Y(t)〉依概率值1等于该过程的集合均值μY(t),则称过程{Y(t),t∈T} 的均值具有各态历经性。同样,若随机过程的时间相关函数〈Y(t)y(t+τ)〉 依概率值1等于该随机过程的集合相关函数RY(t,t+τ),则称过程{Y(t),t∈T}的集合相关函数具有各态历经性。
如果随机过程的均值和集合相关函数均具有各态历经性,则该随机过程具有各态历经性。
随机过程的平稳性和各态历经性特征综合说明,随机过程的各个样本函数都同样地经历了该过程的各种可能状态。因此从任何一个样本函数中都可以得到随机过程的全部信息,任何一个样本函数的特性都可以充分代表整个随机过程的特性。该特性是根据实测得到的一个或少数几个样本来估计平稳随机过程的均值、相关函数等统计量的理论依据。
2 桥梁随机车流类型过程的构建 2.1 动态称重(WIM)系统简介动态称重(Weigh-in-Motion,WIM)系统由埋置于桥面车道上具有一定间距的两道弯板或压电石英和数据采集处理系统组成。当车辆通过时,由弯板或压电石英感应轮胎压力,由数据采集系统记录轮胎压力和作用时刻,进而换算成各车辆轮轴的数量、重量、轮轴间距和车辆速度等。该系统方便快捷且不妨碍车辆通行,可实现对公路上的车辆信息进行自动大容量调查采集,为桥梁车辆荷载的研究工作提供有利条件[7, 9]。
2.2 车辆信息的采集利用WIM系统,分别在广东省内的G107国道、京港澳高速公路(G4)、京珠高速公路(G4w)、虎门大桥(G9411)、沈海高速公路(G15)、虎门渡口东引道(S358)等公路上,连续进行昼夜不间断无人值守的现场实测采集。共历时逾400 d获得逾2.4×107 veh的车辆信息[9]。
2.3 随机车流类型状态空间的建立文献[9]论述了以常见车辆轮轴数量进行划分的合理性,并将车辆划分为2轴小车和2~6轴货车。不失一般性,用数值1表示没有车辆出现的状态,用数值2,…,7表示出现上述车辆的状态。以此记录从0时刻开始各时刻公路桥梁某车道断面上所出现的车辆类型所对应的状态,则Y(t) 的状态空间为{1,2,3,4,5,6,7}。 在各个时刻t,yi(t) 的取值为状态空间中的一个随机变量。
这样便可以用随机过程{Y(t),t∈T}来记录在一定时间内桥上所通过的各类车辆情况。显然,对于不同运营环境和桥梁上的不同车道,车辆出现的概率不同,其随机过程{Y(t)}也各不相同。
2.4 基于实测车辆信息的随机车流类型过程构建文献[9]通过WIM系统进行现场实测,得到6条公路上共28条车道上的大量车辆信息,但为节省存储空间,WIM系统仅记录了出现车辆的时刻而舍弃了没有车辆的状态,这些车辆之间的时间间隔为服从某一分布类型[10]的不等时间间隔。而进行随机过程分析需要以一定的等时间间隔恢复没有车辆出现的状态,这需要选取一个合理的时间间隔Δt,当车辆的时间间隔超过Δt 时,内插若干个没有车辆出现的状态,相当于以1/Δt 的采样频率采集得到公路上的随机车流类型过程。
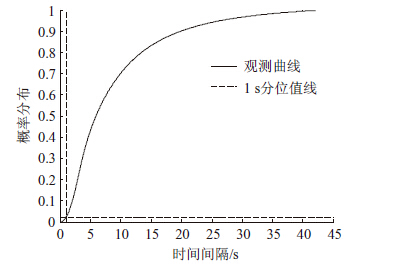
图 2为对车辆之间的时间间隔统计概率分布曲线,曲线上0.05分位值点所对应的时间间隔为1.42 s。为方便计算,取Δt=1 s,其对应的分位值为0.023,即实际公路上有97.7%的车辆之间时间间隔超过1 s,即认为在此间隔内不会连续出现两辆车,符合公路上的实际情况。
|
| 图 2 车辆时间间隔的概率分布曲线 Fig. 2 Probability distribution curve of time intervals of vehicles on highway |
据此,由实测桥上某车道上的车辆信息,从某0时刻开始,由WIM系统记录得到出现车辆的时刻ti和ti+1,用车辆类型对应的Y(t)值标记,在ti与ti+1之间以Δt=1 s间隔用没有车辆出现对应的Y(t)值标记。分别构建得到28条车道的随机车流类型过程。
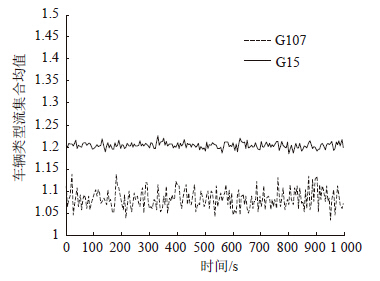
3 随机车流类型过程的数字特征 3.1 集合均值集合平均研究的是同一随机过程各时间点上可能状态取值的均匀性情况。为此,可将所构建的随机车流类型过程划分为任意的N段,则对各段同一序号的观测值y(ti),认为是状态空间{Y(t)}的可能取值,依据式(1)计算得到所有样本函数的集合均值μY(ti)。不失一般性,各段的时长均取1 000 s,计算得到所构建的28条车道上各随机车流序列的集合均值,如图 3和表 1所示。
|
| 图 3 G4和G107公路随机车流类型过程的集合均值 Fig. 3 Ensemble averages of stochastic process of traffic flow type on G107 and G4 |
| 线路名 | 车道号 | 集合均值 | 时间均值 | ||||
| 分段数 | 平均值 | 变异系数 | 段长/s | 平均值 | 变异系数 | ||
| G107 | 1 | 260 | 1.085 | 0.020 | 260 | 1.086 | 0.020 |
| 2 | 510 | 1.126 | 0.019 | 510 | 1.126 | 0.026 | |
| 3 | 190 | 1.113 | 0.029 | 190 | 1.113 | 0.037 | |
| 4 | 317 | 1.107 | 0.019 | 317 | 1.107 | 0.028 | |
| 5 | 537 | 1.143 | 0.020 | 537 | 1.143 | 0.041 | |
| 6 | 350 | 1.098 | 0.020 | 350 | 1.098 | 0.019 | |
| S358 | 1 | 227 | 1.168 | 0.031 | 227 | 1.168 | 0.047 |
| 2 | 168 | 1.105 | 0.033 | 168 | 1.105 | 0.030 | |
| G15 | 1 | 8 537 | 1.218 | 0.007 | 8 537 | 1.218 | 0.046 |
| 2 | 10 202 | 1.203 | 0.005 | 10 202 | 1.203 | 0.032 | |
| G4 | 1 | 1 190 | 1.202 | 0.024 | 1 190 | 1.202 | 0.022 |
| 2 | 1 742 | 1.222 | 0.020 | 1 742 | 1.222 | 0.042 | |
| 3 | 1 081 | 1.109 | 0.014 | 1 081 | 1.109 | 0.029 | |
| 4 | 1 074 | 1.115 | 0.015 | 1 074 | 1.115 | 0.030 | |
| 5 | 1 747 | 1.238 | 0.020 | 1 747 | 1.238 | 0.034 | |
| 6 | 1 360 | 1.215 | 0.023 | 1 360 | 1.215 | 0.027 | |
| G4w | 1 | 978 | 1.205 | 0.021 | 978 | 1.205 | 0.039 |
| 2 | 1 304 | 1.211 | 0.014 | 1 304 | 1.211 | 0.057 | |
| 3 | 1 074 | 1.168 | 0.011 | 1 074 | 1.168 | 0.045 | |
| 4 | 1 219 | 1.166 | 0.010 | 1 219 | 1.166 | 0.043 | |
| 5 | 1 332 | 1.211 | 0.015 | 1 332 | 1.211 | 0.043 | |
| 6 | 1 053 | 1.192 | 0.019 | 1 053 | 1.192 | 0.034 | |
| G9411 | 1 | 30 081 | 1.135 | 0.002 | 30 081 | 1.135 | 0.025 |
| 2 | 28 428 | 1.154 | 0.003 | 28 428 | 1.154 | 0.024 | |
| 3 | 26 489 | 1.173 | 0.004 | 26 489 | 1.173 | 0.025 | |
| 4 | 24 396 | 1.129 | 0.002 | 24 396 | 1.129 | 0.026 | |
| 5 | 26 813 | 1.165 | 0.003 | 26 813 | 1.165 | 0.027 | |
| 6 | 23 889 | 1.183 | 0.004 | 23 889 | 1.183 | 0.031 | |
同样,将所构建的随机车流类型过程划分为任意的N段进行分析。按照式(2)计算各车道上的随机车流类型过程的集合相关函数。
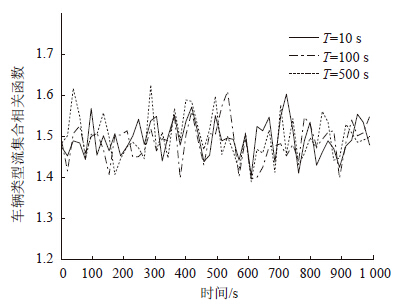
不失一般性,按时长1 000 s进行分段,分别取τ为5,10,50,100,500,1 000 s这6个不同时间间隔进行计算。限于篇幅,表 2仅给出了各条公路上1条主车道的计算结果,图 4给出G4高速公路主车道上不同时间间隔的相关函数的计算结果。
|
| 图 4 G4主车道随机车流类型过程的集合相关函数 Fig. 4 Collection of correlation functions of stochastic process of traffic flow type on main lane of G4 |
| 线路名 |
时间 间隔/s | 集合相关函数 | 时间相关函数 | 分段数 | ||
| 平均值 | 变异系数 | 平均值 | 变异系数 | |||
| G107 | 5 | 1.270 | 0.027 | 1.270 | 0.056 | 510 |
| 10 | 1.270 | 0.027 | 1.270 | 0.055 | ||
| 50 | 1.268 | 0.027 | 1.269 | 0.054 | ||
| 100 | 1.268 | 0.028 | 1.268 | 0.054 | ||
| 500 | 1.268 | 0.029 | 1.269 | 0.047 | ||
| 1 000 | 1.269 | 0.039 | 1.269 | 0.047 | ||
| S358 | 5 | 1.380 | 0.050 | 1.380 | 0.098 | 227 |
| 10 | 1.371 | 0.048 | 1.371 | 0.095 | ||
| 50 | 1.368 | 0.046 | 1.368 | 0.091 | ||
| 100 | 1.365 | 0.045 | 1.364 | 0.084 | ||
| 500 | 1.363 | 0.047 | 1.363 | 0.070 | ||
| 1 000 | 1.364 | 0.063 | 1.364 | 0.071 | ||
| G15 | 5 | 1.490 | 0.011 | 1.490 | 0.092 | 10 202 |
| 10 | 1.486 | 0.011 | 1.486 | 0.088 | ||
| 50 | 1.474 | 0.010 | 1.474 | 0.082 | ||
| 100 | 1.456 | 0.009 | 1.456 | 0.071 | ||
| 500 | 1.448 | 0.008 | 1.448 | 0.066 | ||
| 1 000 | 1.448 | 0.011 | 1.448 | 0.066 | ||
| G4 | 5 | 1.483 | 0.030 | 1.483 | 0.083 | 1 742 |
| 10 | 1.493 | 0.032 | 1.493 | 0.084 | ||
| 50 | 1.496 | 0.032 | 1.496 | 0.085 | ||
| 100 | 1.495 | 0.033 | 1.495 | 0.085 | ||
| 500 | 1.495 | 0.033 | 1.495 | 0.085 | ||
| 1 000 | 1.496 | 0.043 | 1.496 | 0.084 | ||
| G4w | 5 | 1.365 | 0.017 | 1.365 | 0.087 | 1 074 |
| 10 | 1.368 | 0.018 | 1.368 | 0.089 | ||
| 50 | 1.366 | 0.017 | 1.366 | 0.088 | ||
| 100 | 1.366 | 0.017 | 1.366 | 0.088 | ||
| 500 | 1.366 | 0.017 | 1.366 | 0.088 | ||
| 1000 | 1.366 | 0.023 | 1.366 | 0.087 | ||
| G9411 | 5 | 1.301 | 0.003 | 1.301 | 0.053 | 30 081 |
| 10 | 1.290 | 0.003 | 1.290 | 0.051 | ||
| 50 | 1.290 | 0.003 | 1.290 | 0.050 | ||
| 100 | 1.290 | 0.003 | 1.290 | 0.050 | ||
| 500 | 1.290 | 0.003 | 1.290 | 0.050 | ||
| 1 000 | 1.290 | 0.004 | 1.290 | 0.050 | ||
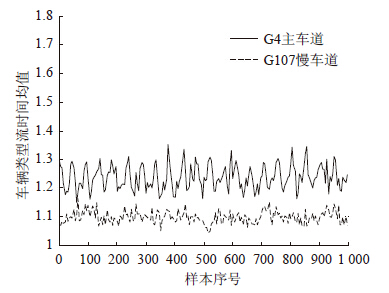
时间均值将每段随机车流过程进行时间平均后归结于1个值,若划分为若干段则有若干个相应值。这样,与上述集合均值的分段方法相反,将各车道上的随机车流类型过程划分成长度为N的1 000个样本,按照式(4)分别计算得到一个时间均值〈Y(t)〉,得到各车道上1 000个样本的时间均值,其结果一并汇总列于表 1,以便对比分析。图 5给出了G4和G107上某车道随机车流过程各1 000个样本时间均值的计算结果。
|
| 图 5 G4和G107随机车流类型过程的时间均值 Fig. 5 Time means of stochastic process of traffic flow type on G4 and G107 |
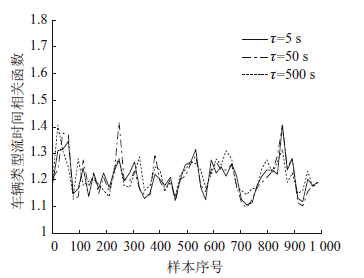
将上述各车道随机车流类型过程所划分的1 000个样本,按照式(5)分别计算得到时间相关函数均值。同样,仅将各条公路上1条主车道的计算结果列于表 2,以便对比分析。图 6为S358主车道上的随机车流类型过程在不同时间间隔下的计算结果。
|
| 图 6 S358主车道随机车流类型过程的时间相关函数 Fig. 6 Time correlation functions of stochastic process of traffic flow type on main lane of S358 |
由图 3和表 1可见,各车道上随机车流类型的集合均值基本上在一条直线附近摆动。从集合均值的变异系数看,这种摆动的幅度比较微小。同时,不同车道上的车辆构成不同,其摆动中心也不同,表明不同车道上的车辆构成和运行状态均不同。
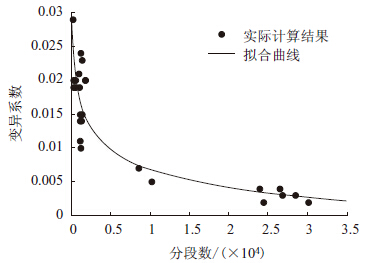
进一步分析表 1中各车道随机车流类型过程的分段数N与集合均值的变异系数之间的关系。图 7一并给出了1条拟合曲线。可以发现,集合均值的变异系数随分段数量N的增加而减小,当N足够大时,集合均值的计算结果将因变异系数的减小而呈现一稳定值μY,表明由WIM系统所记录的车辆信息越多,集合均值越趋于稳定值。
|
| 图 7 集合均值计算的分段数与变异系数关系 Fig. 7 Relationship between variable coefficient and number of sections while calculating ensemble means |
由图 4所示G4主车道上的随机车流类型过程看,其集合相关函数基本上在同一区域内分布着,没有呈现出随时间而变化的趋势。而且按不同时间间隔τ所计算的结果基本在同一区域内重叠,与具体的时间间隔τ无关。此外,集合相关函数的变异系数随着记录数据的增加而减小。
由式(3)知,所构建的这些随机车流类型过程是平稳的,即各公路上的随机车流是平稳的。
4.2 各态历经性分别由所构建随机车流类型过程,按不同的分段方法,对不同段间横向计算其集合均值和纵向计算其时间均值,结果列于表 1。两者几乎一致,唯一不同的是随着分段数N的增加而减小的变异系数,说明了二者相等的依概率性,按式(4)验证了该过程均值的各态历经性。
同样,由表 2给出的集合相关函数和时间相关函数也有同样的结果,按式(5)验证了该过程的集合相关函数具有各态历经性。
由上述平稳性和各态历经性的检验结果,公路上的随机车流类型具有平稳性和各态历经性。
5 结论(1)由WIM系统记录得到公路上车流信息,构建得到车辆随机车流类型过程,真实反映了公路上的随机车流类型状态。
(2)按照随机过程理论,检验了所构建的公路随机车流类型的平稳性和各态历经性。结果表明,各车道上的车流类型具有平稳性和各态历经性特征。
(3)随着车流调查信息量的增加,所构建的随机车流类型过程的平稳性和各态历经性更加稳定,为今后车辆信息的统计和荷载随机模型的建立提供了指导依据。
| [1] | 杨果岳. 车辆随机荷载与柔性路面相互作用的研究[D]. 长沙:中南大学,2007. YANG Guo-yue. Study on Interaction between Vehicle Random Loads and Flexible Pavement[D]. Changsha: Central South University, 2007. |
| [2] | GB/T 7031—1986, 车辆振动输入路面平度表示方法[S]. GB/T 7031—1986, Vehicle Vibration-Describing Method for Road Surface Irregularity[S]. |
| [3] | 党栋,贺拴海,周勇军,等.基于车辆统计数据的汽车荷载标准值取值与评估[J]. 长安大学学报: 自然科学版, 2012,32(6):44-51. DANG Dong, HE Shuan-hai, ZHOU Yong-jun, et al. Choosing and Assessment for the Standard of Vehicle Load Based on Vehicle Statistical Data[J]. Journal of Chang'an University: Natural Science Edition, 2012, 32(6):44-51. |
| [4] | 王涛. 高速公路桥梁交通荷载调查分析及仿真模拟[D]. 西安:长安大学,2010. WANG Tao. Investigation and Simulation of Traffic Loadings on Expressway Bridge[D]. Xi'an: Chang'an University,2010. |
| [5] | 阮欣,周小燚,郭济.基于合成车流的桥梁车辆荷载效应极值预测[J].同济大学学报, 2012, 40(10): 1458-1462. RUAN Xin, ZHOU Xiao-yi, GUO Ji. Extreme Value Extrapolation for Bridge Vehichle Load Effect Based on Synthetic Vehicle Flow[J]. Journal of Tongji University: Natural Science Edition, 2012,40(10):1458-1462. |
| [6] | 李春前. 基于 GPD 模型的车辆荷载效应极值估计[D]. 北京:清华大学, 2012. LI Chun-qian. Research on Extreme Value of Vehicle Load Effect Based on GPD Model[D]. Beijing: Tsinghua University,2012. |
| [7] | 王强,刘仰韶,张文忠, 等. 光纤高速汽车动态称重系统[J]. 长安大学学报:自然科学版, 2014, 34(3): 145-150. WANG Qiang, LIU Yang-shao, ZHANG Wen-zhong, et al. High Speed WIM Based on FBG for Vehicles [J]. Journal of Chang'an University: Natural Science Edition, 2014,34(3):145-150. |
| [8] | 申鼎煊. 随机过程[M]. 武汉:华中路工大学出版社,1990. SHEN Ding-xuan. Stochastic Process [M]. Wuhan: Huazhong University of Science and Technology Press,1990. |
| [9] | 王强,刘仰韶.公路桥梁汽车的轮轴特征[J].公路交通科技,2013, 30(11):41-52. WANG Qiang, LIU Yang-shao. Characters of Wheel Axles of Vehicles on Highway Bridge[J]. Journal of Highway and Transportation Research and Development, 2013,30(11):41-52. |
| [10] | 公路桥梁车辆荷载研究课题组. 公路桥梁车辆荷载研究[J]. 公路,1997(7):8-12. Group of Highway Bridge Vehicle Load Research Project. Research of Highway Bridge Vehicle Loads[J]. Highway,1997(7):8-12. |
 2015, Vol. 31
2015, Vol. 31

 ,
,