扩展功能
文章信息
- 吴幸华, 刘军, 严绍洋
- WU Xing-hua, LIU Jun, YAN Shao-yang
- 流沙层注浆数值模拟研究
- Numerical Simulation of Grouting in Drift Sand Strata
- 公路交通科技, 2015, Vol. 31 (3): 109-116
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 109-116
- 10.3969/j.issn.1002-0268.2015.03.018
-
文章历史
- 收稿日期:2014-07-22
2. 江西省高速公路投资集团有限责任公司, 江西 南昌 330008
2. Jiangxi Expressway Investment Group Co., Ltd., Nanchang Jiangxi 330008, China
流沙层是矿山、隧道工程中经常遇到的一种地质结构,流沙层中的主要成分为粉细砂,粉细砂具有颗粒细小、无黏聚力、自稳能力差的特点,含水粉细砂地层经常发生突涌水等地质灾害[1, 2, 3, 4]。注浆是治理流沙层突涌水灾害的有效手段,通过采用注浆技术,提高流沙层的抗渗性和固结强度,使工程中存在的流沙层由不稳定状态变为稳定状态,安全系数大幅度提高,施工安全得到保障,还节省了用于维护的施工成本。
目前对流沙层注浆的研究大多处在经验总结阶段,理论研究远远落后于工程实践。注浆材料方面,针对水泥浆液、无机类浆液、有机类浆液的流型及黏度特性进行了研究,提出了一系列特征流变方程[5, 6]。试验研究方面,针对无水多孔介质渗透试验、静水条件下的驱水试验、动水条件下的堵水试验方面进行了研究,提出了一系列的各注浆参数之间的回归关系式[7]。渗透注浆理论研究方面,基于牛顿流体的扩散过程得到了球形扩散的Maag公式及柱形扩散公式,基于宾汉流体及黏度时变性的浆液也推导了一系列的扩散方程[8, 9]。
上述研究大多是基于静水条件的研究,对于动水注浆研究较少;对于不同浆液在相同流沙层中的注浆过程的比较方面研究较少。针对以上不足,本文基于流体两相渗流理论,并通过有限元计算软件COMSOL Multiphysics对动水条件下的浆液扩散过程进行稳态与瞬态的数值模拟,得到注浆引起的渗流场压力、速率及浆液分布特征,分析了不同浆液对流沙层注浆的适用性及相关参数对注浆扩散过程的影响。
1 粉细砂性质流沙层中的主要成分为粉细砂,粉细砂的工程性质介于砂性土和黏性土之间,在天然状态下,结构松散,密度较低,在自重的作用下即可压密,埋深较大的粉细砂层,密度较大。粉细砂中粒径大于0.075 mm的颗粒超过全部质量的50%,粒径小于0.25 mm的颗粒含量也超过全部质量的50%的砂土。由以往的工程实践和实验室试验,总结出粉细砂土的工程性质:
(1)粉细砂颗粒细小其粒径分布均匀,且粒径范围很小,结构松散,在外界荷载作用下,很容易变形。
(2)粉细砂土体颗粒之间无黏聚力,主要靠取决于粒间法向压力的粒间摩擦力维持本身稳定和承载能力,自稳能力很差。
(3)在被水饱和情况下,粉细砂在荷载作用下的变形速率加大,按变形控制的承载力较低。
(4)粉细砂的渗透系数一般为1.2×10-3~6.0×10-3 cm/s,属于中等透水性。天然沉积粉细砂水平向渗透系数明显大于垂直向渗透系数。
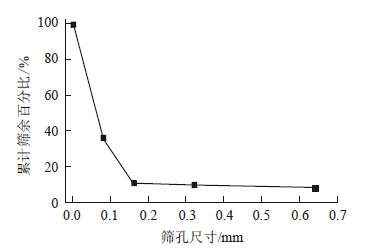
以内蒙古某矿的粉细砂地层为例,取特征性粉细砂土样进行试验分析确定其物理力学参数,对粉细砂的筛分结果见表 1,筛分曲线见图 1。
| 筛孔尺寸/mm | 筛余量/g | 分计筛余百分率/% | 累计筛余百分率/% |
| 0.64 | 41 | 8.2 | 8.2 |
| 0.32 | 8 | 1.6 | 9.8 |
| 0.16 | 5 | 1 | 10.8 |
| 0.08 | 126 | 25.2 | 36 |
| 0 | 317 | 63.4 | 99.4 |
|
| 图 1 粉细砂筛分曲线图 Fig. 1 Curve of fine sand screening |
从筛分曲线可以看出粉细砂的粒径分布比较均匀,且粒径范围很小,超过60%的粒径小于80 μm。根据现场水井抽水试验结果,得流沙层渗透系数K=0.73~128.25 m/d,经过换算取渗透率为5.0×10-12 m2进行研究。
2 注浆有限元模型创建 2.1 控制方程采用流体两相渗流理论描述动水条件下的浆液扩散过程,通过COMSOL Multiphysics 中多孔介质和地下水流模块中的两相Darcy定律物理场进行求解。认为粉细砂为各向同性的不可压缩介质,水及浆液均为不可压缩的各向同性流体,所采用的控制方程如下:
浆液质量守恒方程:
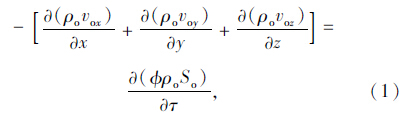
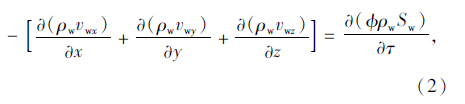




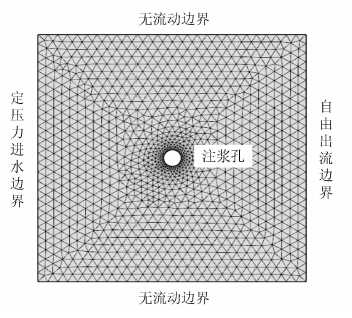
注浆有限元模型为二维正方形,模型尺寸为0.3 m×0.3 m,注浆管位于模型正中间,注浆管直径为2 cm,左边界为定压力进水边界,右边界为自由出流边界,上下边界为无流动边界,注浆管处注浆压力恒定。选用水玻璃、矿粉-水玻璃、超细水泥3种工程上常用的3种注浆材料,设置注浆压力范围 1×104~5×104 Pa进行水、浆液两相渗流模拟。
|
| 图 2 计算模型及网格剖分结果图 Fig. 2 Calculation model and meshing result |
根据实测的粉细砂地层参数及浆液流变参数确定被注介质及浆液参数,为形成动水流场,设定进水压力为20 kPa,计算模型参数如表 2所示。
| 属性 | 水玻璃 | 矿粉-水玻璃 | 超细水泥 |
| 水的密度/(kg·m-3) | 1 000 | ||
| 水的黏度/(Pa·s) | 0.001 | ||
| 浆液密度/(kg·m-3) | 1 350 | 1 100 | 1 500 |
| 浆液黏度/(Pa·s) | 0.004 | 0.003 | 0.012 |
| 孔隙率 | 0.05 | ||
| 渗透率/m2 | 5×10-12 | ||
| 进水压力/Pa | 20 000 | ||
| 注浆压力/Pa | 2×104 | ||
| 出流边界压力/Pa | 0 |
本文先研究天然地下水在流沙层中的单相渗流特点和静水条件下的浆液扩散特点,然后再分析动水条件下浆液扩散规律和不同注浆材料、不同注浆压力对浆液扩散的影响,最后对水、浆液两相不稳定渗流过程进行数值模拟,分析浆液的动态扩散特点。
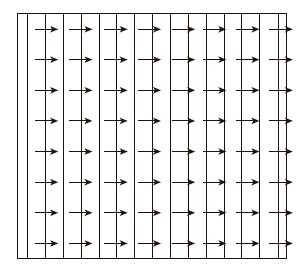
3.1 天然地下水流场模拟3.1 天然地下水流场模拟 水的单相渗流速度在整个渗流场中均匀分布,速度大小为3.27×10-4 m/s。速度方向从进水边界水平指向出水边界。渗流场中的压力从进水边界到出水边界均匀递减,在渗流场中同一x坐标对应的点压强相等。渗流场流网中的等压力线和流线均为直线且等间隔正交分布。
|
| 图 3 天然地下水流场渗流压力等值线分布 Fig. 3 Contours of seepage pressure of natural groundwater flow field |
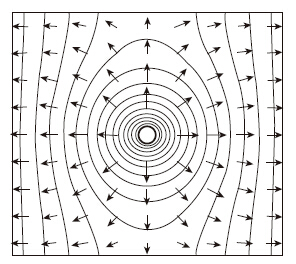
3.2 静水条件下浆液扩散过程模拟 静水条件下浆液扩散的计算结果如图 4、图 5所示。浆液在静水条件下渗流的压力以注浆口为中心向周围衰减,压力分布图形在注浆口附近接近圆形、在边界附近呈波形向两侧边界排列。在注浆口处等压线密集,在边界附近等压线稀疏。浆液从注浆口流入渗流场,从两侧边界流出渗流场。在注浆口处压力梯度最大、渗流速度也最大,在边界附近压力梯度小、渗流速度比较小。

|
| 图 4 注浆压力2×104 Pa下渗流压力场分布 Fig. 4 Distribution of seepage pressure under grouting pressure of 2×104 Pa |
|
| 图 5 注浆压力2×105 静水条件下浆液扩散压力等值线分布 Fig. 5 Contours of slurry diffusion pressure in hydrostatic state |
动水条件下浆液扩散的计算结果如图 6、图 7所示。不同条件下的浆-水两相稳定渗流场具有相似的特点。在出流边界两端附近速度大、中间速度小。注浆口顺水流方向速度大、逆水流方向端速度小并且速度方向水平向左,这是注浆口附近存在逆水流扩散的直接原因。在注浆口左侧一段距离处存在一个速度接近零的区域。在进水边界速度变化不大并且速度方向都是向右的,这说明水是流入的。

|
| 图 6 两相渗流速度场分布 Fig. 6 Distribution of velocity field of two-phase seepage |
|
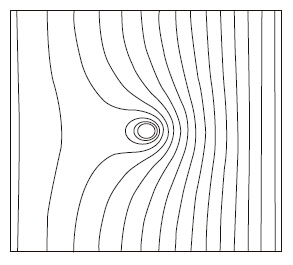
| 图 7 两相渗流压力场分布 Fig. 7 Distribution of pressure field of two-phase seepage |
渗流场压力从进水边界和注浆口向出流边界衰减,在注浆口逆水流方向压力沿逆水流方向衰减,在注浆口和进水边界之间存在一个压力极小值点。从图 7可以看出在渗流场的右半段等压线密集,在渗流场左半段等压线稀疏。注浆口顺水流方向等压线比较密集,逆水流方向等压线比较稀疏。
浆液体积分数分布见图 8。地下水流影响了浆液扩散分布的形状,浆液在渗流场中大致呈钟形分布且都存在逆水流扩散区域,浆液在注浆口附近体积分数、浓度最高,离注浆口越远体积分数、浓度越低。浆液与水之间没有明显的分界面而是存在一个过渡区,体积分数为0.4~0.6的过渡区域宽度不是很大。

|
| 图 8 浆液体积分数分布图 Fig. 8 DDistribution of slurry volume fraction |
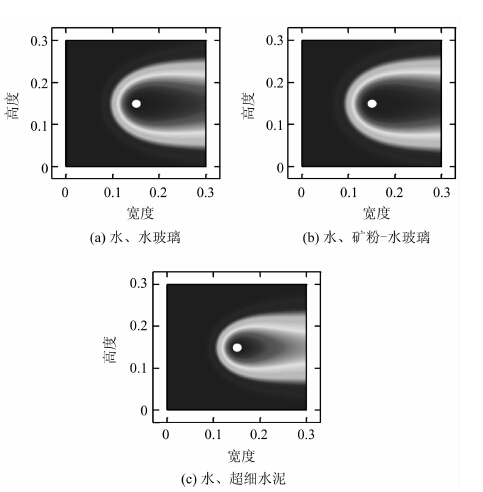
不同注浆材料影响浆液扩散形状和扩散范围,如图 9所示。浆液的黏度越低扩散范围越大,黏度越高扩散范围越小。因为浆液的黏度不同,渗流过程中遇到的阻力就不同,浆液黏度越大,渗流过程中阻力越大,相应的扩散范围就越小。
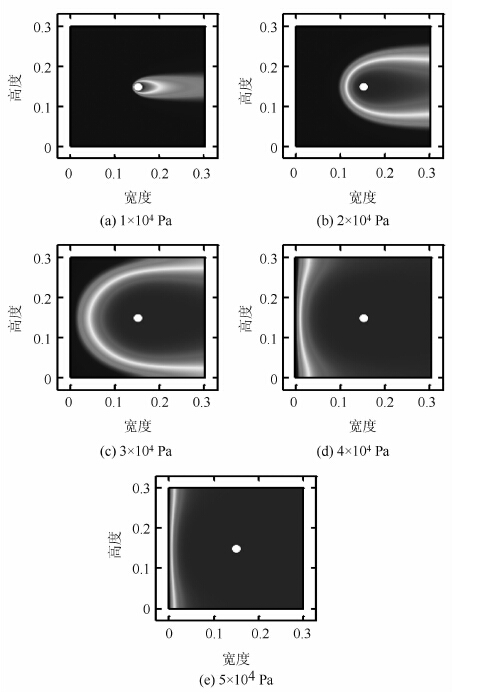
五种注浆压力对应的浆液体积分数分布对比见图 10。不同注浆压力主要影响浆液扩散形态和扩散范围。在1×104 Pa注浆压力条件下浆液仅仅扩散了很小一个区域,随着注浆压力的升高,浆液扩散范围不断增加,当注浆压力达到4×104 Pa时浆液几乎充满整个模型空间。注浆压力越大扩散范围越大,随着注浆压力升高,渗流场中的压力梯度也升高,由达西渗透定律可得渗流场中的渗流速度升高,扩散范围也更大。
|
| 图 9 三种注浆材料的浆液体积分数分布对比图(单位:m) Fig. 9 Contrast of slurry volume fractions of 3 grouting materials(unit:m) |
|
| 图 10 五种注浆压力对应的浆液体积分数分布对比图(单位:m) Fig. 10 Contrast of slurry volume fractions of 5 grouting pressures(unit:m) |
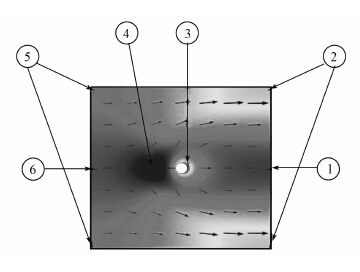
取渗流场中的6个特征点比较不同条件下的速度大小(图 11)。
|
| 图 11 特征点分布图 Fig. 11 Distribution of feature points |
不同注浆材料对速度场的影响如表 3所示。不同注浆材料对速度场分布的影响主要是速度的大小,3种不同注浆材料渗流场的特征点速度大小如表 3所示。其中3点为速度最大点也是浆液流出速度最大点。
| 注浆材料 | V1 | V2 | V3 | V4 | V5 | V6 |
| 水玻璃 | 1.4 | 4.4 | 6.3 | 0 | 2.0 | 1.5 |
| 矿粉水玻璃 | 1.7 | 4.5 | 8.2 | 0 | 1.9 | 1.4 |
| 超细水泥 | 1.1 | 4.0 | 3.1 | 0 | 2.3 | 1.9 |
从表 3中可以看出3种注浆材料在出流边界的速度大小:矿粉-水玻璃>水玻璃>超细水泥;速度最大值:矿粉-水玻璃>水玻璃>超细水泥;进水边界的速度大小:矿粉-水玻璃<水玻璃<超细水泥。不同的注浆材料对于渗流场的影响主要是黏度因素的影响,其他因素的影响很小,从表 3可以得出随着黏度的降低,出流边界的速度升高,进水边界的速度降低,速度最大值升高。黏度的降低使进水量减少,浆液注入量增加。
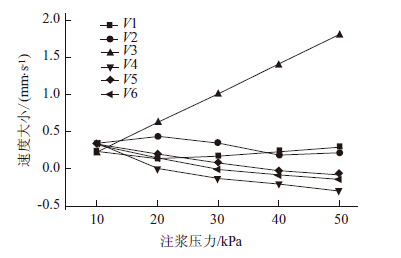
不同注浆压力条件对渗流场速度的影响如图 12所示。图中纵坐标的负值表示速度方向向左。水的 单相渗流速度大小为3.27×10-4 m/s。注浆压力为1×104 Pa的渗流场中除了1和3点与水的单相渗流速度相差比较大,其他4个点处渗流速度大小基本一致,在1点和3点之间的狭长区域中,浆液填充其中,从浆液体积分数分布图中可以看出在这个狭长区域内流动的液体中浆液占了很大比例,而在这个狭长区域之外的液体基本上都是水。这说明在注浆口处以1×104 Pa的注浆压力注浆对水在渗流场中的渗流只在注浆口以后的一段狭长区域有影响,对大部分区域影响不大。
|
| 图 12 不同特征点速度随注浆压力变化曲线 Fig. 12 Relationship between velocity of feature point and grouting pressure |
随着注浆压力的变化各个特征点处渗流速度的变化特点:1×104 Pa注浆压力下,1点和3点处的渗流速度低于水单相渗流速度,随着注浆压力的升高1点处的渗流速度先降低后升高,3点处的渗流速度不断升高。液体原来的渗流流动是由进水边界和出流边界之间的压力差驱动,在注浆口处注浆对于原来液体在1点和3点的流动起阻碍作用,降低了1点和3点处的液体渗流速度。随着注浆口注浆压力升高,对于原来液体的阻碍作用也增加,所以1点处的渗流速度随着注浆压力的升高而降低,但是当注浆压力升高到一定数值时,注浆口和出流边界之间的压力差对1点处渗流的影响将超过进水边界和出水边界之间压力差对1点处渗流的影响,并且注浆口和出流边界之间的压力差所引起的1点处渗流速度方向也为水平向右的,随着注浆压力继续升高渗流速度也随着逐渐升高,这是1点处渗流速度先降低后升高的原因。3点处因为离注浆口太近,所以注浆口注浆压力对3点渗流的影响远大于对1点渗流的影响,并且也大于进水边界和出水边界之间压力差对3点渗流的影响,注浆口注浆压力对3点的渗流速度起决定作用,随着注浆压力的升高,3点处的压力梯度也升高,其渗流速度也不断升高。
4,5,6点处的渗流速度从正值到零然再到负值,即速度先变小到零然后又逐渐增大,5、6点处的渗流速度变为负值说明有浆液扩散到进水边界并且从进水边界流出。综上所述,注浆口和进水边界之间存在一个压力极小值点,这个压力极小值点随着注浆压力的升高向进水边界移动,在这个点右侧渗流速度向左,左侧渗流速度向右,在注浆压力从1×104 Pa升高到5×104 Pa的过程中压力极小值点从4点的右侧移动到2×104 Pa中的4点然后继续向左移动,所以4点的渗流速度正值到零然再到负值。随着注浆压力的升高,4,5,6点处压力梯度由向右逐渐变为向左,压力梯度大小逐渐减小到零然后不断增大,所以这3个点处的渗流速度从向右逐渐变为向左,渗流速度大小逐渐减小到零然后不断增大。从上述分析可以看出随着注浆压力的升高,注浆口处注浆压力对渗流速度的影响不断增大并且逐渐超过两侧边界之间水力差对渗流速度的影响,在水、浆液两相渗流中动水的影响逐渐变小、注浆的影响逐渐变大。
3.6 水、浆液两相不稳定渗流过程由于浆液体积分数分布图最能体现浆液扩散的动态过程,所以选择浆液体积分数分布图进行研究,在具有代表性的时间点截取浆液体积分数分布图并将分布图按时间顺序排列以方便观察。
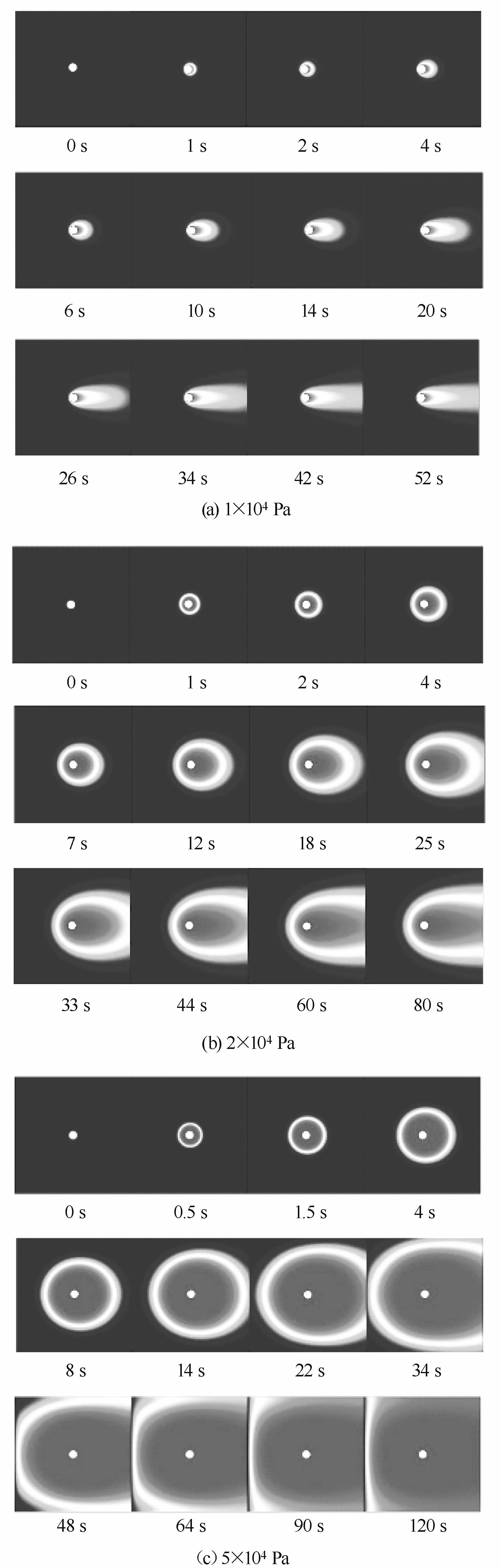
3种注浆压力对应的注浆扩散过程中浆液体积分数分布变化规律有相似的特点,见图 13。随着时间增长浆液从注浆口逐渐向四周扩散,在浆液扩散过程中明显伴随着浆液等饱和度面的移动,刚开始浆液扩散范围接近圆形,之后在注浆口的右侧浆液扩散范围增加得比左侧快,经过一段时间达到接近稳定渗流的状态。之所以在注浆口的右侧浆液扩散范围增加的比左侧快是因为水在渗流场中流动的影响,水的渗流速度是从左侧界面指向右侧界面的,这必然导致浆液向左边的扩散受阻,从而使等饱和度面的中心在注浆口的右侧。在浆液还没有扩散到渗流场边界时,等饱和度面内的面积由从注浆口注入的浆液量Q决定。随着时间的增长等饱和度面内的面积不断增大直至浆液扩散到渗流场边界,再过一段时间,浆液渗流到达稳定阶段,等饱和度面内的面积保持稳定不变。
|
| 图 13 浆液体积分数分布随时间变化图 Fig. 13 Distribution of slurry volume fraction varying with time |
从图中可以看出注浆压力不同,两相渗流达到稳定渗流的时间也不相同,1×104 Pa注浆压力下大约50 s达到稳定渗流,2×104 Pa下大约需要80 s,5×104 Pa下大约需要120 s。随着注浆压力的升高,两相渗流达到稳定渗流状态所需要的时间也边长。
4 结论(1)基于达西定律通过数值计算软件COMSOL Multiphysics 实现了流沙层注浆的数值模拟。
(2)浆液在渗流场中大致呈钟形分布且都存在逆水流扩散区域,浆液与水之间没有明显的分界面而是存在一个过渡区。压力从进水边界和注浆口向出流边界衰减,在注浆口逆水流方向压力沿逆水流方向衰减,在注浆口和进水边界之间存在一个压力极小值点并存在一个速度接近零的区域。
(3)注浆材料对注浆的影响主要体现在黏度方面,黏度对渗流场压力分布的影响不大但显著影响渗流场速度。黏度影响浆液扩散的形状和范围,浆液黏度越低扩散范围越大。随着注浆压力的增加,浆液扩散范围不断增加,两相渗流达到稳定渗流状态所需要的时间也变长。
| [1] | 李术才,韩伟伟,张庆松,等. 地下工程动水注浆速凝浆液黏度时变特性研究[J]. 岩石力学与工程学报,2013,32(1): 1-7. LI Shu-cai,HAN Wei-wei,ZHANG Qing-song,et al. Research on Time-dependent Behavior of Viscosity of Fast Curing Grouts in Underground Construction Grouting [J] Chinese Journal of Rock Mechanics and Engineering, 2013,32(1): 1-7. |
| [2] | 房凯,夏唐代,包柳青,等. 考虑滤过效应的卵砾石层浆液扩散研究[J]. 岩石力学与工程学报,2013,32(7): 1443-1448. FANG Kai, XIA Tang-dai, BAO Liu-qing, et al. Cement Grout Dispersion Considering Filtration in Gravel [J]. Chinese Journal of Rock Mechanics and Engineering, 2013,32(7): 1443-1448. |
| [3] | 李术才,刘人太,张庆松,等. 基于黏度时变性的水泥-玻璃浆液扩散机制研究[J]. 岩石力学与工程学报,2013,32(12): 2415-2421. LI Shu-cai,LIU Ren-tai,ZHANG Qing-song,et al. Research on C-S Slurry Diffusion Mechanism with Time-dependent Behavior of Viscosity [J]. Chinese Journal of Rock Mechanics and Engineering, 2013,32(12): 2415-2421. |
| [4] | 肖建平,王凡,朱自强,等. 预应力孔道超声检测回波法数值模拟的频散特性分析[J]. 公路交通科技,2014,31(2): 74-80. XIAO Jian-ping, WANG Fan, ZHU Zi-qiang,et al. Analysis of Dispersion Characteristics of Numerical Simulation of Prestressed Duct Using Ultrasonic Detection Echo Method[J]. Journal of Highway and Transportation Research and Development, 2014,31(2): 74-80. |
| [5] | 叶飞,苟长飞,陈治,等. 盾构隧道粘度时变性浆液壁后注浆渗透扩散模型[J]. 中国公路学报,2013,26(1): 127-134. YE Fei, GOU Chang-fei, CHEN Zhi, et al. Back-filled Grouts Diffusion Model of Shield Tunnel Considering Its Viscosity Degeneration[J]. Chinese Journal of Highway and Transport,2013,26(1): 127-134. |
| [6] | 孙斌堂,凌贤长,凌晨,等. 渗透注浆浆液扩散与注浆压力分布数值模拟[J]. 水利学报, 2007,37(11):1402-1407. SUN Bin-tang, LING Xian-chang, LING Chen, et al. Numerical Simulation for Diffusion and Pressure Distribution of Permeation Grouting[J]. Journal of Hydraulic Engineering, 2007,37(11):1402-1407. |
| [7] | 阮文军. 基于浆液粘度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2005,24(15): 2709-2714. RUAN Wen-jun. Spreading Model of Grouting in Rock Mass Fissures Based on Time-dependent Behavior of Viscosity of Cement-based Grouts[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(15): 2709-2714. |
| [8] | 郭院成,张景伟,董晓星. 桩端桩侧后注浆钻孔灌注桩承载性能试验研究[J]. 公路交通科技, 2014,31(7): 14-18. GUO Yuan-cheng, ZHANG Jing-wei ,DONG Xiao-xing. Experimental Study on Bearing Capacity of Bored Piles Using Pile Tip and Side Post-grouting Technology[J]. Journal of Highway and Transportation Research and Development, 2014,31(7): 14-18. |
| [9] | 张霄.地下工程动水注浆过程中浆液扩散与封堵机理研究及应用[D].济南:山东大学,2011. ZHANG Xiao. Study on Mechanism of Slurry Diffusion and Sealing at Process of Underground Engineering Moving Water Grouting and Its Application[D].Jinan: Shandong University,2011. |
| [10] | 刘人太. 水泥基速凝浆液地下工程动水注浆扩散封堵机理及应用研究 [D]. 济南:山东大学,2012. LIU Ren-tai. Study on Diffusion and Plugging Mechanism of Quick Setting Cement Based Slurry in Underground Dynamic Water Grouting and Its Application [D]. Jinan: Shandong University,2012. |
| [11] | 朱明听. 单一裂隙注浆扩散及封堵机理的数值模拟研究[D].济南:山东大学, 2013. ZHU Ming-ting. Numerical Simulation of Grouting Diffusion and Plugging Mechanism Based on Single Fracture [D]. Jinan: Shandong University,2013. |
| [12] | 张庆松,韩伟伟,李术才,等. 灰岩角砾岩破碎带涌水综合注浆治理[J]. 岩石力学与工程学报,2012,31(12):2412-2419. ZHANG Qing-song,HAN Wei-wei,Li Shu-cai,et al. Comprehensive Grouting Treatment for Water Gushing Analysis in Limestone Breccias Fracture Zone[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(12): 2412-2419. |
| [13] | 杨志全,侯克鹏,郭婷婷,等. 基于考虑时变性的宾汉姆流体的渗透注浆机理研究[J]. 四川大学学报:工程科学版, 2011,43(増1): 67-72. YANG Zhi-quan, HOU Ke-peng, GUO Ting-ting, et al. Study on Penetration Grouting Mechanism Based on Bingham Fluid of Time-dependent Behavior[J]. Journal of Sichuan University: Engineering Science Edition, 2011,43(S1): 67-72. |
 2015, Vol. 31
2015, Vol. 31
