扩展功能
文章信息
- 聂洪琳, 熊文, 曹毅, 吕文, 叶见曙
- NIE Hong-lin, XIONG Wen, CAO Yi, LÜ Wen, YE Jian-shu
- 桥墩防落石碰撞柔性设计方法及分析
- Design Method and Analysis of a Flexible Anti-collision Structure of Bridge Piers
- 公路交通科技, 2015, Vol. 31 (3): 96-102
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 96-102
- 10.3969/j.issn.1002-0268.2015.03.016
-
文章历史
- 收稿日期:2014-04-17
2. 东南大学 交通学院, 江苏 南京 210096;
3. 江西省公路科研设计院, 江西 南昌 330002;
4. 江西省公路机械工程局, 江西 南昌 330026
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China;
3. Jiangxi Highway Research and Design Institute, Nanchang Jiangxi 330002, China;
4. Jiangxi Highway Mechanical Engineering Bureau, Nanchang Jiangxi 330026, China
山区公路大型山体滑坡现象日益严重,在我国山区地区的省市尤为明显。一旦发生山体滑坡并伴随落石时,暴露于落石运动路线中的桥墩很容易被落石撞击而导致结构受损,进而影响其承载力及耐久性能,甚至还发生过桥墩遭巨石撞击引起严重开裂并最终拆除重建的实例,从而导致高速公路网的长时间交通中断。例如2011年成雅高速公路曾发生山体滑坡伴随大量落石,造成周边桥墩受损,部分桥墩甚至存在落梁隐患。随着西部建设开发的不断发展,对于山区桥梁桥墩的防落石撞击研究已成为山区桥梁设计理论的一个重要课题[1]。
目前国内外针对桥墩防落石碰撞设计主要以防撞设施与桥墩结构一体化的设计为主,例如在桥墩上安装橡胶装置。显然这种设计无法将落石与桥墩隔离,一旦防撞措施失效或者材料耐久性能下降,桥墩变会直接承受落石的撞击,存在一定的风险。独立桥墩的防落石碰撞措施是近期的研究热点,该种设计可以完全将落石以及落石运动轨迹与桥墩隔离,最大化保证桥墩在落石环境下的安全。
此外,关于桥梁防撞的计算分析主要集中于船桥碰撞或车桥碰撞方面,很少有文献涉及山区落石-桥墩防撞物之间的碰撞动力学分析,更没有统一的防撞设计理念[1, 2, 3, 4, 5, 6, 7, 8, 9]。虽然相关规范提供简单的解析解直接计算碰撞冲击力,由于把一个动态的力学作用简化成静态分析,往往计算结果与实际情况相差甚远[3, 4, 5, 6]。所以,落石-桥墩防撞物之间的碰撞相互作用的精细化分析显得尤为重要,是进行桥墩防落石碰撞的理论工具。
本研究基于动力学基本原理,分别从非线性、接触以及本构关系3个角度选择合适的计算理论建立落石-桥墩防撞物碰撞精细化计算模型,并对关键计算参数给出建议取值;同时利用钢结构柔性变形吸收落石碰撞能量,提出一种桥墩防落石碰撞柔性设计方法,并详细给出该防落石碰撞构造措施的组成形式;进而基于所提出的精细化碰撞模型,采用ANSYS/LS-DYNA计算模块,数值仿真滚石撞击防撞物的动态全过程。本研究以一个偏安全的极限碰撞状态,分别从运动行为(撞击力、位移、速度以及加速度)以及能量转换(系统动能以及系统变形能)角度进行数据分析,证明所提出的柔性防撞设计思路的合理性与优越性,为今后此类结构设计或建立相关规程提供理论参考。
1 计算理论落石撞击桥墩防撞物是一个瞬态的高强度冲击过程,在很短的时间内碰撞区附近的构件发生塑性变形、屈曲、褶皱、崩溃以及撕裂。从力学角度来看,是一个非常复杂的考虑几何、材料非线性的接触动力学问题。
1.1 非线性有限元控制方程一般来说,碰撞问题采用拉格朗日方法建立其非线性有限元控制方程[10]:

式(1)经有限元离散处理后,按结构瞬态动力学问题采用显式中心差分法进行求解。时间步长按式(2)计算得到,即采用最小有限单元网格的特征长度除以应力波速来定义:
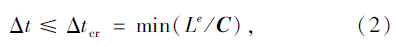
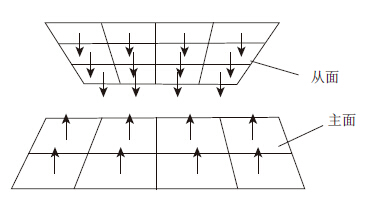
有限元理论模拟碰撞过程,相撞结构(或构件)之间的相互作用是通过接触算法来完成的。在可能发生接触作用的结构之间定义一组接触面,该组接触面能有效地模拟相撞结构之间的相互作用,并允许结构之间连续地接触和滑动。在滚石撞击桥墩防撞物时相互接触的面分别定义为主面和从面,面上的节点称为主节点和从节点,见图 1。
|
| 图 1 主从接触面 Fig. 1 Master-slave contact surface |
本次研究中接触算法采用对称罚函数法,在求解的每一时间步,检查从面上的从节点是否已经穿透主面,如果还没有穿透,则计算工作继续进行;否则在垂直于主面的方向上施加一作用力以阻止从节点的进一步穿透,这个作用力就是接触力,其大小与穿透深度、接触刚度成正比,这个接触力亦成为罚函数值,接触力由式(3)计算:

采用对称罚函数法时同时对主节点进行处理,其算法同从节点一样。对称罚函数法具有对称性,计算准确,但罚函数值受到计算稳定性的限制,若计算中出现明显的穿透,可用放大罚函数值或缩小时间步长来调整。
1.3 材料本构模型在本次研究对象桥墩防落石碰撞柔性设计计算中存在两种基本材料,其本构模型按如下方法分别确定。
(1)钢材材料特性
落石与钢材构件碰撞时,碰撞区域构件将发生钢材的弹塑性大变形(以塑性变形为主),显然钢材的材料本构关系是碰撞分析中的重要参数。为真实反映材料特性,钢材采用线性强化弹塑性模型,其屈服应力为:
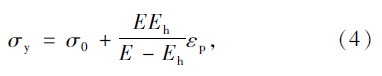
采用假定失效准则来判断钢材材料的实效与否。按假定失效准则,单元的等效塑性应变超过定义的极限塑性应变时,单元便发生断裂失效。为使有限元单元的计算断裂状况与实际钢材的物理断裂一致,需要正确定义单元材料的断裂应变极限值。事实上,这一参数取值在有限元理论中受到单元网格尺度的影响。其次,在落石与钢材碰撞作用的动态响应过程中,低碳钢的塑性性能对应变率是高度敏感的,必须在材料模型中引入应变率敏感性的影响。本研究中采用试验数据吻合得比较好的Cowper-Symonds本构方程来考虑屈服应力与应变率的关系[10]:
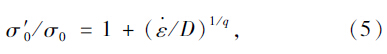
(2)滚石材料特性
本研究中滚石材料选取刚性体模型,即不考虑滚石材料本身的破坏,这样可以偏安全地检验桥墩防撞物的防撞效果。所选取的滚石材料常数取值分别为:弹性模量E=5×1010 N/m2;密度ρ=2 690 kg/m3;泊松比υ=0.24。
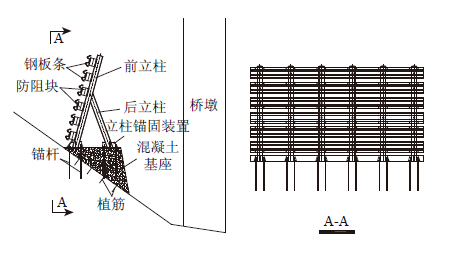
2 柔性防撞设计方法与计算 2.1 桥墩柔性防撞物设计基于桥墩钢套箱柔性防船撞的基本设计思路[3, 11, 12],采用钢结构柔性变形来吸收落石碰撞能量,提出一种柔性防撞的新型桥墩设计思路。总体结构设计图如图 2所示。
|
| 图 2 防撞装置总体布置图 Fig. 2 General arrangement of anti-collision structure |
具体来说,该装置包括若干钢板条、防阻块、前立柱、后立柱、立柱锚固装置、基座(图 2)。其中,钢板条呈波纹状,分别固定于防阻块,而防阻块固定安装于前立柱,前立柱一端被后立柱一端所支撑,同时前立柱与后立柱的另一端由立柱锚固装置固定于基座,形成一个稳定的三角支撑结构,基座直接沿陡坡山体修建。该桥墩柔性防落石碰撞装置面对滚石运动前进方向修建,并位于需要防护的桥墩前方。
该桥墩防撞物设计具有以下特点:
(1)局部提供撞击缓冲。采用波纹状钢板条形成滚石直接碰撞面,该撞击面局部呈波纹形状,适合多种角度的滚石碰撞,在局部可以提供撞击缓冲。
(2)动能-变形能转换耗能。当落石滚动碰撞至波纹状钢板条后,波纹状钢板条发生明显变形,利用滚石动能转化为钢板条变形能的方式进行吸能。
(3)材料局部屈服耗能。当落石滚动碰撞至波纹状钢板条后,部分波纹状钢板条会严重变形直至屈曲,这时钢材发生屈曲材料破坏而释放大量能量,从而达到对滚石动能进行耗能的作用。
(4)三角支撑结构。该结构可防止滚石撞击瞬间冲击力过大而导致该桥墩防滚石碰撞装置发生整体结构失稳现象,从而失去防滚石碰撞功效。
(5)可更换设计。波纹状钢板条在遭到碰撞变形之后可进行快速局部更换修复。
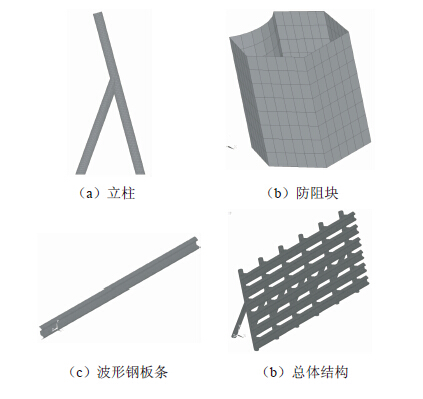
2.2 有限元模型建立验证该桥墩柔性防撞物的设计思想,主要是验证桥墩防撞物的防撞效果,即研究其吸收碰撞能的效果,关键在于获得落石-防撞装置之间的瞬态撞击力及撞击过程中滚石运动速度、加速度等关键运动参数随撞击时间的变化情况。所以在建立落石-桥墩防撞物碰撞仿真分析非线性有限元模型时,在碰撞区域要进行单独单元加密以达到计算精细化;同时为提高计算效率,在非碰撞区域可将建模的精细程度适当放宽。本文采用ANSYS/LS-DYNA大型有限元软件,按第2节所提出的计算理论与模型对软件进行二次开发,选择合适的计算模块与单元,并对材料属性进行单独自定义输入,最终建立有限元模型见图 3。单元和节点数见表 1。整个柔性装置共计节点75 462个,单元72 912个。防阻块与立柱之间,以及防阻块与波形板之间均采用节点耦合的办法进行联结,立柱底部节点固结。为计算极限碰撞工况,此处陡坡斜率偏安全的取为45°倾斜角。
|
| 图 3 防撞装置有限元模型图 Fig. 3 Finite element model of anti-collision structure |
| 构件名称 | 构件个数 |
单件 节点数 |
单件 单元数 |
全部 节点数 |
全部 单元数 |
| 立柱 | 6 | 3 040 | 3 000 | 18 240 | 18 000 |
| 防阻块 | 24 | 324 | 288 | 7 776 | 6 912 |
| 波形板 | 6 | 8 241 | 8 000 | 49 446 | 48 000 |
| 合计 | — | — | — | 75 462 | 72 912 |
按既有参考文献统计数据,碰撞中滚石采用直径为0.5 m的球体,其碰撞前初始速度取为20 m/s,基本大于实际情况下滚石碰撞桥墩时的瞬时速度[2, 7, 13]。滚石模型采用SOLID164单元,共建立5 223 个单元,1 111个节点,如图 4所示。

|
| 图 4 滚石有限元模型图 Fig. 4 Finite element model of rolling stone |
相互接触结构(或构件)之间的相互作用通过接触算法来完成。在可能发生接触作用的结构之间定义接触面,接触面能有效地模拟相撞结构之间的相互作用,并允许结构之间连续的接触和滑动。在ANSYS/LS-DYNA中,接触类型可分为3类,即单面接触、节点-表面接触、表面-表面接触。本文采用自动单面接触(ASSC)和自动面-面接触(ASTS),静、动摩擦系数均采用0.1。(此处如有实际现场试验取值则可进一步提高计算的精确度)。
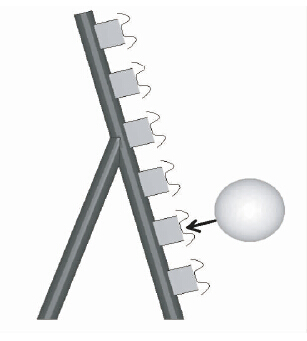
2.3 碰撞计算结果分析本文针对落石垂直撞击防撞措施这一工况按上文中提出的方法进行精细化分析。滚石以20 m/s的撞击前初始速度,沿45°坡角滚落并垂直撞击至桥墩防撞物,所谓垂直撞击是指滚石垂直于6道波形板所在的平面进行撞击,初始相对位置关系及速度方向示意如图 5所示。针对计算结果的后处理采用LS-PREPOST软件进行。
|
| 图 5 初始位置及速度方向示意(垂直撞击) Fig. 5 Initial location and velocity direction (vertical impact) |
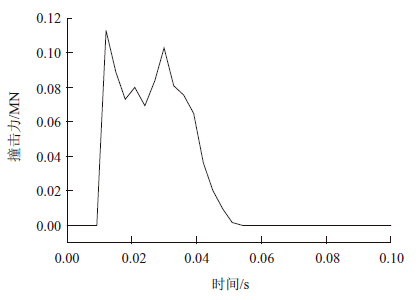
经过显示动力学分析,撞击力随时间的变化曲线如图 6所示。防护装置所受撞击力具有很强的非线性波动特征,碰撞力的每一次峰值卸载都代表了防护装置的某个构件的局部屈服。最大撞击力0.113 MN,约出现在t=0.012 s时刻,此后被撞波形板的两个波峰后陷,并向上下伸展,同时该波形板所连的防阻块发生向中央的剪切变形,因此撞击力卸载之后很快迎来了第2个撞击力峰值0.103 MN,约出现在t=0.03 s 时刻。整个撞击过程起始于t=0.009 s时刻,结束于t=0.054 s时刻,共持续0.045 s。
|
| 图 6 撞击力时程曲线 Fig. 6 Impact force vs. time |
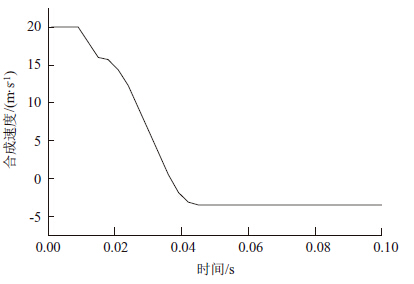
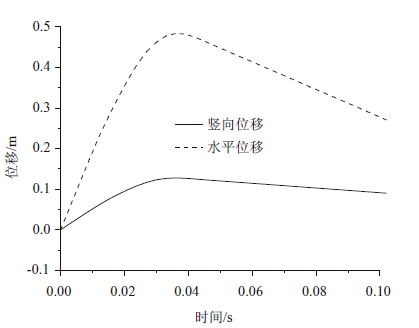
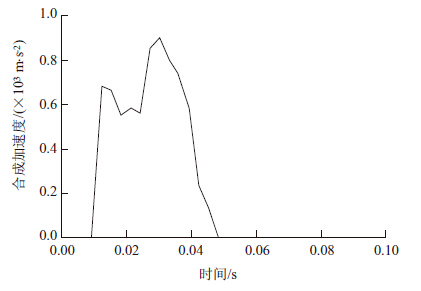
落石速度如图 7所示,落石在波形板的拦截下速度迅速减小到0,然后减小为负值,说明落石此时已被弹回。落石最终的剩余速度仅为3.4 m/s,即使再次从山坡上滚下,也不会对防护装置造成损伤。图 8中给出的落石位移时程曲线也能说明这一点。落石加速度时程曲线如图 9所示,加速度的量值整体上经历了一个先增大后减小的过程,分别对应落石入侵防护装置和被防护装置弹回的过程。
|
| 图 7 落石速度时程曲线 Fig. 7 Rolling stone velocity vs. time |
|
| 图 8 落石位移时程曲线 Fig. 8 Rolling stone displacement vs. time |
|
| 图 9 落石加速度时程曲线 Fig. 9 Rolling stone acceleration vs. time |
从以上分析中可以看出,本文提出的桥墩防落石碰撞柔性设计方法,在偏安全设计的极限状态下,不仅可以有效拦截落石,而且能够迅速降低它的速度及加速度,最终使其反方向运动并停止,从而达到防止落石直接撞击桥墩的设计目的。
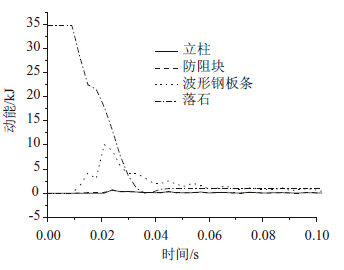
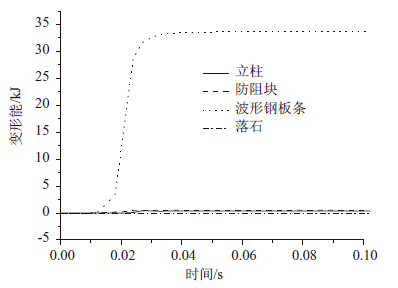
3 碰撞能量分析落石的撞击动能将转化为了这样几种能量:(1) 落石在碰撞结束时刻的剩余动能;(2) 防护装置的弹塑性变形能及动能; (3) 构件之间摩擦引起的热能损失;(4) 计算中由于沙漏现象损失的能量。其中(1)和(2)是主要部分,(3)和(4) 是次要部分,量值很小。图 10给出整个系统的动能时程曲线,落石的动能在撞击开始之后很快衰减,波形钢板条在撞击之初也有部分动能,不过很快衰减。图 11所示为整个系统的变形能时程曲线,波形钢板条是将系统动能转化为变形能的最主要构件。
|
| 图 10 系统动能时程曲线 Fig. 10 Kinetic energy of system vs. time |
|
| 图 11 系统变形能时程曲线 Fig. 11 Deformation energy of system vs. time |
结合图 10、图 11可以看出,最显著的能量转换发生0.01~0.04s之间,即在落石与波形钢板条相撞击的瞬间,之后虽仍有能量装换,但量值均很小。这与前一节位移、速度以及加速度分析所得出的结论也是一致的。这里可参考船撞设计,认为最终动 能向系统内能转化率大于60%[11, 12],即可达到较好的桥墩防撞效果。
另外,在忽略次要因素的情况下,可以发现系统变形能和动能之间虽有转换,但两者之和基本保持不变,符合能量守恒定律。此外,动能在相邻两次撞击之间呈曲线变化,并且前段是下降段,而后段存在微小的上升段。这主要因为重力势能在前段参与消耗动能(动能转势能),而后端虽然增加动能(势能转动能),但是此时速度方向与之前滚石运动方向已经不同甚至相反了。
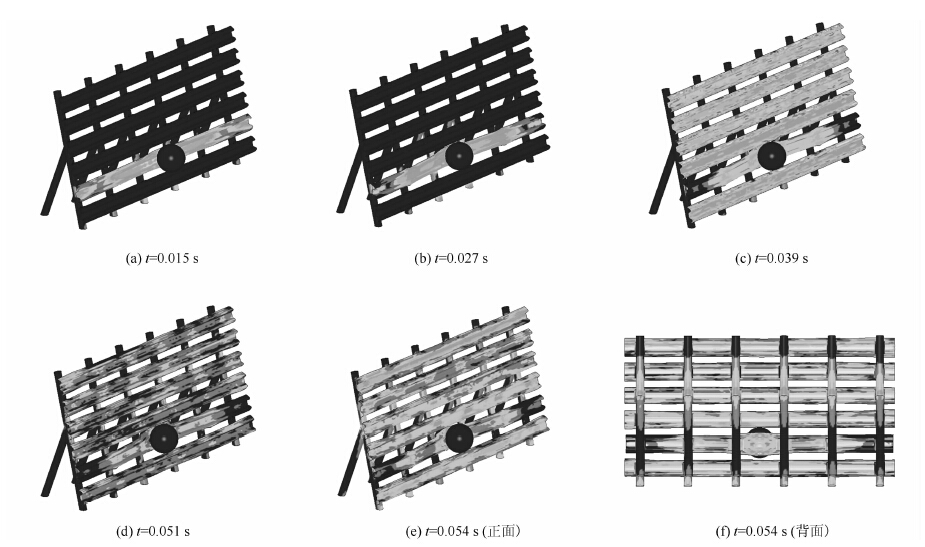
图 12给出了各时刻桥墩防撞物材料应变云图,从材料变形角度更加直观地观察这种能量的转化。可以看出,在0.01~0.04 s之间波形钢板条迅速发生剧烈变形,从而基本完成落石动能与波形钢板条变形能的转变,与该柔性防撞的设计思路完全符合。
|
| 图 12 各时刻桥墩防撞物材料应变云图 Fig. 12 Nephogram of strain of pier anti-collision material at different times |
本文基于动力学基本理论,分别从非线性、接触以及本构关系3个角度分别选择合适的计算理论建立滚石-桥墩防撞物之间的碰撞耦合精细化动态模型,并对关键计算参数给出建议取值;同时提出一种桥墩防落石碰撞柔性设计方法,利用钢结构柔性变形来吸收落石碰撞能量;并以一个偏安全的极限碰撞状态,分别从运动行为(撞击力、位移、速度以及加速度)以及能量转换(系统动能以及系统变形能)角度证明这一设计思路的合理性与优越性。
| [1] | 沈均, 何思明, 吴永. 滚石灾害研究现状及发展趋势[J]. 灾害学, 2008, 23(4), 225-231. SHEN Jun, HE Si-ming, WU Yong. Present Research Status and Development Trend of Rockfall Hazards[J]. Journal of Catastrophology, 2008, 23(4), 225-231. |
| [2] | 叶四桥, 陈洪凯, 唐红梅. 落石冲击力计算方法的比较研究[J]. 水文地质工程地质, 2010, 37(2): 59-64. YE Si-qiao, CHEN Hong-kai, TANG Hong-mei. Comparative Research on Impact Force Calculation Methods for Rockfalls[J]. Hydrogeology & Engineering Geology, 2010, 37(2), 59-64. |
| [3] | 孙振. 桥梁防船撞设施的比较研究[D]. 上海:同济大学, 2007. SUN Zhen. Comparative Research on Bridge Anti-collision Equipment [D]. Shanghai: Tongji University, 2007. |
| [4] | JTG D60—2004, 公路桥涵设计通用规范[S]. JTG D60—2004, General Code for Design of Highway Bridge and Culverts[S]. |
| [5] | JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. |
| [6] | LAN H, MARTIN C D, ZHOU C, et al. Rockfall Hazard Analysis Using LiDAR and Spatial Modeling [J]. Geomorphology, 2010, 118(1/2): 213-223. |
| [7] | 李兴民, 韩建明, 朱东生, 等. 滚石与桥墩碰撞的数值仿真分析[J]. 重庆交通大学学报, 2011, 30(5): 934-937. LI Xing-min, HAN Jian-ming, ZHU Dong-sheng, et al. Numerical Simulation of Rolling Stone-bridge Pier Collision[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2011, 30(5): 934-937. |
| [8] | MOUGIN J P, PERROTIN P, MOMMESSIN M, et al. Rock Fall Impact on Reinforced Concrete Slab: an Experimental Approach [J]. |
| [9] | SASIHARAN N, MUHUNTHAN B, BADGER T C, et al. Numerical Analysis of the Performance of Wire Mesh and Cable Net Rockfall Protection System [J]. Engineering Geology, 2006, 88(1/2): 121-132. |
| [10] | 殷有泉. 非线性有限元基础[M]. 北京: 北京大学出版社, 2007. YIN You-quan. Basis of Nonlinearity Finite Element [M]. Beijing: Peking University Press, 2007. |
| [11] | 李升玉, 王曙光, 刘伟庆,等. 船舶与桥墩防撞系统碰撞的数值仿真分析[J]. 自然灾害学报, 2006, 15(5): 100-106. LI Sheng-yu,WANG Shu-guang, LIU Wei-qing, et al. Numerical Simulations of Ship Collision with Protective Devices of Bridge Pier[J]. Journal of Natural Disasters, 2006, 15(5): 100-106. |
| [12] | 罗琳. 船桥碰撞理论及猎德大桥防撞装置的性能研究[D]. 长沙:长沙理工大学, 2008. LUO Lin. Ship-bridge Collision Theories and Analysis on Anti-collision Equipment of Liede Bridge[D]. Changsha: Changsha University of Science & Technology, 2008. |
| [13] | 向欣. 边坡落石运动特性及碰撞冲击作用研究[D].武汉:中国地质大学, 2010. XIANG Xin. Research on Motion Characteristics and Impact Force of Rockfall on Slope[D]. Wuhan: China University of Geosciences, 2010. |
 2015, Vol. 31
2015, Vol. 31
