扩展功能
文章信息
- 李胜利, 路毓, 王东炜
- LI Sheng-li, LU Yu, WANG Dong-wei
- 悬索桥骑跨式吊索驰振气动干扰效应数值分析
- Numerical Analysis of Aerodynamic Interference Effect of Galloping on Straddle Sling of Suspension Bridge
- 公路交通科技, 2015, Vol. 31 (3): 82-88
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 82-88
- 10.3969/j.issn.1002-0268.2015.03.014
-
文章历史
- 收稿日期:2014-02-21
2. 河南省许昌市魏都区新型城镇化建设管理委员会办公室, 河南 许昌 461000
2. The New Urbanization Construction Management Committee Office of Weidu District of Xuchang City, Xuchang Henan 461000, China
吊索是在缆索体系桥梁运营期间能对结构安全性产生影响的重要构件之一,也是缆索体系桥梁上最易损害的构件[1]。在类似风振荷载等动力荷载的长期作用下,吊索会由于裂缝扩展和损伤积累达到极限而产生破坏。研究表明[2],在运营期间,高风速作用下,吊索的损伤非常明显。而风又是比较常见的荷载,故由风振荷载产生的吊索疲劳损伤应引起重视。
圆柱群在工程领域很常见,如悬索桥的主缆和吊索、热交换管线组、斜拉桥的斜拉索、电力传输线、核电站的核反应堆等。众所周知,上游圆柱的湍流尾流会诱发下游圆柱产生驰振振荡,当风速超过临界值时,会出现无限制大幅振荡,进而会影响到结构的疲劳寿命,甚至会造成生命财产的损失。因此关于单个圆柱和圆柱群的绕流问题的研究在流体动力学和工程应用中也就显得尤为重要。
关于圆柱绕流问题的研究主要针对单个圆柱和两个圆柱的绕流问题[3],而对于多于两个圆柱绕流问题研究的文献还是相当缺乏的。1977年和1985年研究者对两个钝体间的干扰进行了研究[4],发现当两个钝体的间距达到5d~7d,横向偏移达到1.5d时,两个圆柱体会发生大振幅振动[5]。Meada等利用物理风洞试验对两个圆柱体尾流驰振进行了研究,根据尾流驰振机理,通过使用气动弹性方法研制出一种抑制斜拉桥的斜拉索发生尾流驰振的方法[6]。Tokoro等通过一系列风洞试验对两个电缆的气动稳定性进行了研究[7]。Nagao等对三圆柱体的尾流驰振进行了研究[8]。Hover等研究了圆柱体在上游圆柱体尾流干扰下的驰振响应,发现上游圆柱脱落的涡旋不受下游圆柱运动的影响[9]。Lam等对正方形排列的四圆柱体和柱体群绕流进行了研究:通过物理风洞试验测量了雷诺数在亚临界区域的气动力系数和斯托罗哈数,得出随着l/d的改变,气动力系数和斯托罗哈数由3种明显的流态所控制[10];对在雷诺数为200情况下的流动形态进行了研究,发现根据风攻角流动被分成了3种基本的流态[11];用表面涡方法对柱体群的流致振动进行了数值模拟[12]和使用有限体积法对雷诺数为100和200的顺排排列的正方形布置的四圆柱体进行了二维和三维的数值模拟,发现了通过物理风洞试验很难看到的流体特征和信息;还对雷诺数为200层流流过同样布置的四圆柱进行了三维数值模拟[13]。Zou Lin对雷诺数为200的菱形布置的四圆柱体绕流进行了三维数值模拟,发现间距比严重影响着圆柱自由剪切层的发展、气动力和压力特征[14]。在国内也有学者通过物理风洞试验对斜拉索[15]和主缆[16, 17]进行了研究,黄伟峰对吊杆的尾流驰振问题进行了研究[18]。但至今未见有人对长方形排列的四圆柱尾流驰振气动干扰效应进行研究。
本文在前人研究的基础上,参照某大跨径悬索桥的骑跨式吊索参数设置方法,采用CFD数值模拟方法对长方形排列的四圆柱的驰振气动干扰效应进行研究,为大跨径悬索桥骑跨式吊索的疲劳分析提供基础。
1 阻力和升力系数数值模拟方法根据登哈托准则,驰振力系数的计算是吊索驰振性能分析的必要条件,而驰振力系数的计算又是以阻力和升力系数为基础的,阻力系数(Cd)和升力系数(Cl)的计算公式如下:
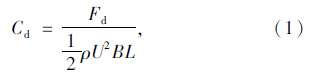
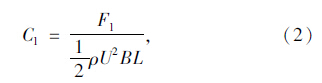
本文数值风洞试验采用的数学模型是不可压雷诺时均N-S方程,采用标准k-ε双方程湍流模型,由于横风向空气流速低,故流动按二维定常不可压处理,也不考虑温度变化的效应,静力计算按定常处理[20]。本文采用有限体积法,模拟雷诺数在亚临界区域的绕流流动,利用Fluent6.1.2计算流体动力学软件模拟计算模型周围流场。采用默认的simple算法解决动量方程中速度分量和压力项耦合的问题,并结合壁面函数法,采用二阶迎风格式,对流项和扩散项等均采用二阶精度计算。计算域的长宽均大于40倍模型的特征长度。
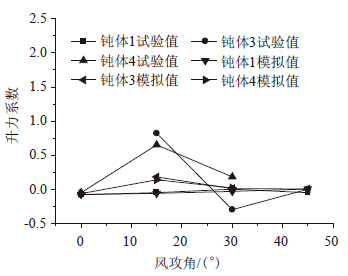
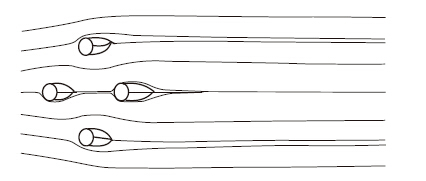
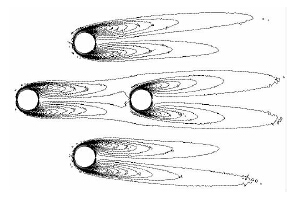
选用文献[21]来验证数值风洞试验参数设置的正确性。由于文献[21]给出了风攻角为0°,15°,30°和45°时的不同l / d (l为钝体间距,d为钝体直径)的平均阻力系数和平均升力系数,且对于各种不同的l / d,钝体3只给出风攻角为15°,30°和45°时的阻力系数和升力系数, 钝体4只给出了0°,15°和30°时的阻力系数和升力系数,故本文针对文献中给出的试验数据,选用 l / d=3.83时钝体一、钝体三和钝体四的数据进行模拟,模拟结果如图 1和图 2所示,图 3和图 4分别是风攻角为45°时四圆柱流线图和涡量等值线图。由图 1和图 2比较可知,本文计算的气动力系数和文献中的气动力系数能很好地吻合,但是还是有一定差异。主要原因:湍流本质上是三维的,而考虑到计算量的问题,进行了平面流动假定;采用的相似比、计算域和单元个数等对结果也有一定影响;不过差异较小,且计算结果的趋势和试验值吻合较好,可以认为本文所采用的数值风洞湍流模型方法具有一定的合理性和有效性。考虑到索的特征频率远低于尾流涡的振荡频率,因此决定尾流驰振的是平均气动力及其导数而非瞬时气动力及其导数,故本文采用定常的湍流流动计算所得的结果较为合理。

|
| 图 1 阻力系数 Fig. 1 Drag coefficients |
|
| 图 2 升力系数 Fig. 2 Lift coefficients |
|
| 图 3 风攻角为45°时的四圆柱流线图 Fig. 3 Streamlines of 4 cylinders in wind attack angle of 45° |
|
| 图 4 风攻角为45°时的四圆柱涡量等值线图 Fig. 4 Vorticity isolines of 4 cylinders in wind attack angle of 45° |
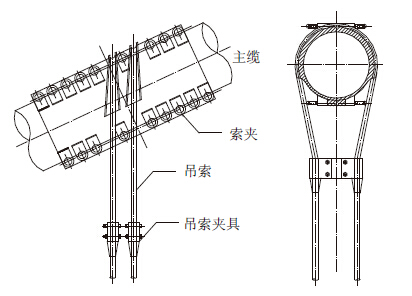
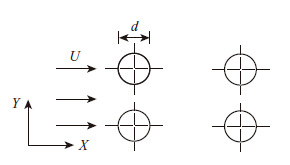
本文研究的对象为某大跨径悬索桥骑跨式吊索,在吊索的设计工况下,Reynolds数为1.7×105,其中该大跨径悬索桥吊索分为一般吊索、北边跨短吊索和北塔处长吊索,因该悬索桥吊索多数为一般吊索,故取一般吊索为研究对象。其中吊索布置图如图 5所示。吊索为顺排长方形排列方式,横桥向间距为600 mm,纵桥向间距为300 mm,吊索直径为60 mm,一般吊索构造图如图 6所示。又因吊索长度远大于直径,故本文将流场计算问题近似转化为平面问题,即计算长方形顺排排列的四圆柱绕流,简化后的示意图如图 7所示。

|
| 图 5 吊索布置图(单位:cm) Fig. 5 Layout of slings(unit:cm) |
|
| 图 6 骑跨式吊索构造 Fig. 6 Structure of straddle sling |
|
| 图 7 吊索绕流示意图 Fig. 7 Schematic diagram of air flow around slings |
下游圆柱的振动方程[22]:
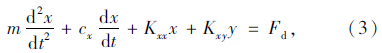
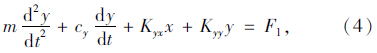
气动力表达式为[18]:
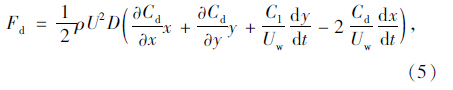

将式(5)和式(6)代入式(3)和式(4),令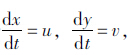 得:
得:
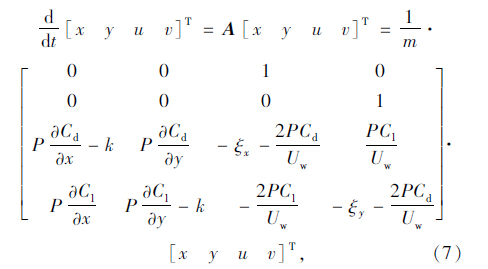
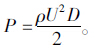
依据常微分方程组解的稳定性理论,通过系数矩阵A的特征值的正负可判断其稳定性,进而判断是否会发生驰振。若式(7)所有的特征值实部均为负,则常微分方程组的解是稳定的不会产生驰振;反之,若式(7)有一个特征值的实部为正,常微分方程组的解就会不稳定,驰振就会发生。由此可见,只要求得式(3)和式(4)中的阻力系数、升力系数及其气动力导数,即可判断是否发生驰振失稳现象。
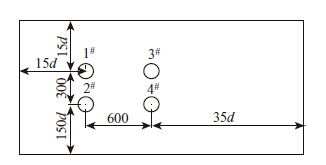
2.2 计算域和网格划分对某大跨径悬索桥的骑跨式吊索进行二维简化,得到顺排排列的四圆柱如图 8所示,其中1#~4#代表四圆柱编号。同时参考文献[23]对计算域进行设定,计算域为60d×35d的矩形区域,其中原点距上游入口为15d,上游柱体距离各自较近边界为15d,下游柱体离下游出口为35d,1#和2#之间的距离参考该骑跨式吊索顺桥向的距离为300 mm,1#和3#之间的距离参考该吊索横桥向的距离为600 mm,其中钝体的直径d为60 mm。雷诺数对圆柱绕流有影响,但在所研究工况的雷诺数下,雷诺数对气动力影响较小,故不予考虑,网格划分采用非结构网格,网格数量大约为45万左右。外边界条件流体进口为速度入口边界条件,上下边界为对称边界条件,也就是上下边界为零滑移壁面,流体出口为压力出口边界条件,内边界均为无滑移边界条件,如图 9所示。
|
| 图 8 长方形顺排排列四圆柱布置图(单位:mm) Fig. 8 Layout of 4 cylinders in rectangle arrangement(unit:mm) |

|
| 图 9 吊索断面网格划分 Fig. 9 Meshing of sling section |
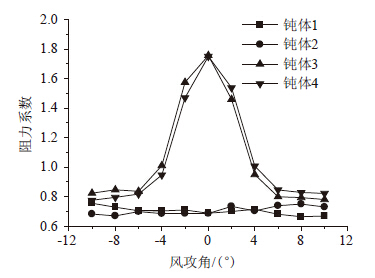
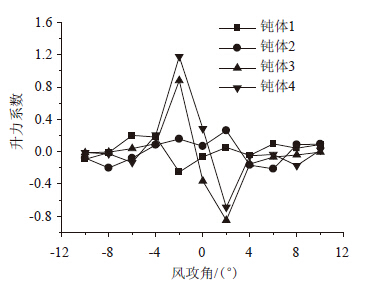
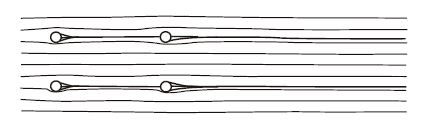
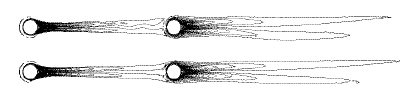
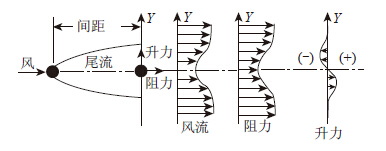
图 10和图 11分别是四圆柱随风攻角变化的阻力系数和升力系数,图 12和图 13为吊索的流线图和涡量等值线图。由图 12和图 13可见,上游2个钝体无论是阻力系数还是升力系数变化都比较平稳。下游2个钝体的变化趋势较为一致。阻力系数在-4°~0°攻角范围内逐渐增大,在0°~4°范围内逐渐减小,在0°攻角的时候达到最大;升力系数在-4°~-2°和2°~4°范围内逐渐增大,在-2°~2°范围内逐渐减小,分别在-2°和2°的时候达到最大,其发生变化的风攻角范围和达到最大的攻角都和2个钝体的阻力和升力的风攻角变化情况(图 14[22])较好地吻合,但是由于上下游钝体之间和下游2个钝体之间气动干扰效应使钝体的阻力系数和升力系数的变化方向和两个钝体时刚好相反,这也说明了多个钝体间的气动干扰效应可能导致下游钝体阻力系数和升力系数的变化方向发生改变。
|
| 图 10 阻力系数 Fig. 10 Drag coefficients |
|
| 图 11 升力系数 Fig. 11 Lift coefficient |
|
| 图 12 风攻角为0°时的流线图 Fig. 12 Streamlines of slings in wind attack angle of 0° |
|
| 图 13 风攻角为0°时的涡量等值线图 Fig. 13 Vorticity isolines of slings in wind attack angle of 0° |
|
| 图 14 两个圆柱时平均速度、升力和阻力分布的定性图 Fig. 14 Qualitative figure of distribution of average velocities,lift and drag forces |
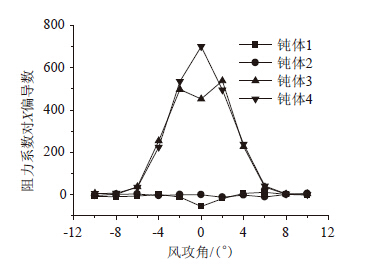
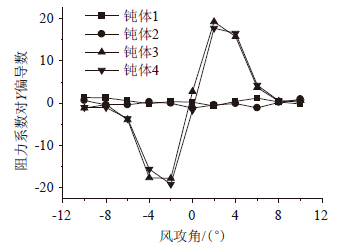
2.4 稳定性分析 通过利用gambit软件将钝体进行旋转来实现对下游钝体的偏移,定义沿着风向为X轴正方向,垂直X轴向上为Y轴正方向,如图 7所示。计算得到阻力和升力系数分别对X轴和Y轴的偏导数如图 15~图 18所示。
|
| 图 15 阻力系数对X轴的偏导数 Fig. 15 Partial derivatives of drag coefficients to x-axis |
|
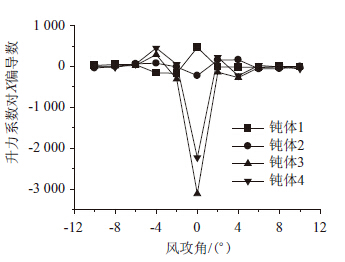
| 图 16 阻力系数对Y轴的偏导数 Fig. 16 Partial derivatives of drag coefficients to y-axis |
|
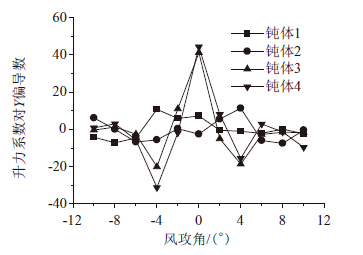
| 图 17 升力系数对X轴的偏导数 Fig. 17 Partial derivatives of lift coefficients to x-axis |
|
| 图 18 升力系数对Y轴的偏导数 Fig. 18 Partial derivatives of lift coefficients to y-axis |
利用得到的平均气动力通过向前差值、向后差值和中心差值法计算得到气动力对X轴和Y轴的偏导数,代入式(7)系数矩阵,利用Matlab计算得到每种风攻角时的系数矩阵的特征值如表 1和表 2所示,根据特征值的正负可判断吊索的驰振稳定性,即特征值都为负时,则是稳定的,不会发生驰振;若特征值有一个为正值,则是不稳定的,会发生驰振,进而可判断吊索在何种情况下会发生驰振。由文献[22]可知,在上下游吊索距离一定的情况下,不稳定区域位于一定的中间区域,即位于小于某一风攻角上限值和大于某一风攻角下限值的区域,此区域以外为稳定区域。
| 攻角/(°) | 特征值 | 状态 |
| -10 | -1.253±29.792i,-1.239 ±36.041i | 稳定 |
| -8 | 0.152±34.548i,-2.714±34.521i | 不稳定 |
| -6 | 28.983,-31.489,-1.279±36.04i | 不稳定 |
| -4 | 113.86,-116.71,-1.63±36.03i | 不稳定 |
| -2 | -1.768,1.713,-0.02±0.36i | 不稳定 |
| 0 | -164.16,163.245,-55.655,45.946 | 不稳定 |
| 2 | 176.39,-180.374,-2.422±35.983i | 不稳定 |
| 4 | 106.833,-109.37,-1.604±36.027i | 不稳定 |
| 6 | 26.912,-29.231,-1.261±36.041i | 不稳定 |
| 8 | -1.394±36.063i,-1.007±34.446i | 稳定 |
| 10 | -1.205±36.042i,-1.157±34.105i | 稳定 |
| 攻角/(°) | 特征值 | 状态 |
| -10 | -1.17±29.543i,-1.177±36.043i | 稳定 |
| -8 | -1.242±36.041i,-1.166±25.745i | 稳定 |
| -6 | -24.907,22.013,-1.027±36.05i | 不稳定 |
| -4 | 102.657,-104.742,-1.824±36.016i | 不稳定 |
| -2 | 176.37,-180.491,-41.694,36.919 | 不稳定 |
| 0 | 202.897,-209.629,31.547,-35.403 | 不稳定 |
| 2 | -175.669,-170.627,-2.132±36.001i | 稳定 |
| 4 | 1.107,-1.137,-0.016±0.36i | 不稳定 |
| 6 | 37.009,-39.591,-1.268±36.04i | 不稳定 |
| 8 | -1.751±36.14i,-0.756±33.628i | 稳定 |
| 10 | -1.124±42.263i,-1.365±36.034i | 稳定 |
由表 1和表 2可见,钝体3在风攻角为-8°~6°范围内处于不稳定状态,钝体4在风攻角为-6°~ 0°和4°~6°范围内处于不稳定状态,即下游两个钝体都存在不稳定区域,但由于钝体间气动干扰的存在,使得两个钝体的不稳定区域不一致,同时,也和两个钝体的驰振不稳定区域[22]有所差异,但基本上是符合的。由此可知,在设计给出的参数下,该大跨悬索桥的吊索在一定攻角范围内将发生驰振,对桥梁的安全性产生威胁,当采取减振措施后可能会影响吊索的疲劳性能。
3 结论(1)下游钝体阻力系数在-4°~0°攻角范围内 逐渐增大,在0°~4°范围内逐渐减小,在0°攻角时达到最大;升力系数在-4°~-2°和2°~4°范围内逐渐增大,在-2°~2°范围内逐渐减小,分别在-2°和2°的时候达到最大。
(2)矩形排列4个钝体的下游2个钝体的阻力和升力系数发生变化的风攻角范围与2个钝体的情况吻合较好,但由于钝体间气动干扰效应使其下游钝体的阻力和升力系数的变化方向与2个钝体的情况相反。
(3)在风荷载作用下,下游2个钝体均存在不稳定区域,可能会发生驰振,且由于气动干扰效应,下游2个钝体的不稳定区域与2个钝体的情况不同。
| [1] | WASTON S C, STAFFORD D. Cables in Trouble [J]. Civil Engineering, 1988,58(4): 38-41. |
| [2] | 胡俊, 欧进萍. 风载作用下悬索桥吊索腐蚀疲劳寿命分析 [J]. 钢结构, 2011, 26(5): 63-67. HU Jun, OU Jin-ping. The Corrosion Fatigue Life Analysis on Hangers of Long Span Suspension Bridge under Wind Load[J]. Steel Construction, 2011, 26(5): 63-67. |
| [3] | SUMNER D. Two Circular Cylinders in Cross-flow: A Review [J]. |
| [4] | ZDRAVKOVICH M M, PRIDDEN D L. Interference between Two Circular Cylinders: Series of Unexpected Discontinuities[J]. |
| [5] | ZDRAVKOVICH M M. Flow Induced Oscillations of Two Interfering Circular Cylinders [J]. |
| [6] | MAEDA H,KUBO Y,KATO K,et al. Aerodynamic Characteristics of Closely and Rigidly Connected Cables for Cable-stayed Bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69: 263-278. |
| [7] | TOKORO S,KOMATSU H,NAKASU M,et al. A Study on Wake-galloping Employing Full Aeroelastic Twin Cable Model [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2): 247-261. |
| [8] | NAGAO F, UTSUNOMIYA H, NODA M, et al. Aerodynamic Properties of Closed Spaced Triple Circular Cylinders [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1): 75-82. |
| [9] | HOVER F S, TRIANTAFYLLOU M S. Galloping Response of A Cylinder with Upstream Wake Interference [J]. Journal of Fluids and Structures, 2001, 15(3): 503-512. |
| [10] | LAM K, LI J Y, SO R M C. Force Coefficient and Strouhal Numbers of Four Cylinders in Cross Flow [J]. Journal of Fluids and Structures, 2003, 18(3): 305-324. |
| [11] | LAM K, LI J Y, SO R M C, et al. Flow Pattern and Velocity Field Distribution of Cross-flow Around Four Cylinders in A Square Configuration at A Low Reynolds Number [J]. Journal of Fluids and Structures, 2003, 17(5): 665-679. |
| [12] | LAM K, JIANG G D, LIU Y, et al. Simulation of Cross-flow-induced Vibration of Arrays by Surface Vorticity Method [J]. Journal of Fluids and Structures, 2006, 22(8): 1113-1131. |
| [13] | LAM K, ZOU L. Three-dimensional Numerical Simulations of Cross-flow around Four Cylinders in A In-line Square Configuration [J]. Journal of Fluids and Structures, 2010, 26(3): 482-502. |
| [14] | ZOU L. Flow Patterns and Force Characteristics of Laminar Flow Past Four Cylinders in Diamond Arrangement [J]. Journal of Hydrodynamics: Ser. |
| [15] | 李永乐, 王涛, 廖海黎. 斜拉桥并列拉索尾流驰振风洞试验研究 [J]. 工程力学, 2010, 27(増1): 216-221. LI Yong-le, WANG Tao, LIAO Hai-li.Investigation on Wake Galloping of Parallel Cables in Cable-stayed Bridge by Wind Tunnel Test[J]. Engineering Mechanics, 2010, 27(S1): 216-221. |
| [16] | 胡建华, 赵跃宇, 刘慕广, 等. 串列双索气弹模型的风洞试验研究 [J]. 动力学与控制学报,2006,4(2):179-186. HU Jian-hua, ZHAO Yue-yu, LIU Mu-guang, et al. Wind Tunnel Studies on the Behaviour of Aeroelastic Twin Cable Model[J]. Journal of Dynamics and Control, 2006, 4(2 ): 179-186. |
| [17] | 陈政清, 刘慕广, 祝志文. 基于气弹模型的串列主缆气动干扰试验研究 [J]. 振动与冲击, 2008, 27(8):7-11. CHEN Zheng-qing, LIU Mu-guang, LIU Zhi-wen. Experiment Study on Aerodynamic Interference of Tandem Cables Based on Aeroelastic Model[J]. Journal of Vibration and Shock, 2008,27(8):7-11. |
| [18] | 黄伟峰,李勇,刘秋生,等. 桥梁吊杆索尾流驰振问题的数值研究 [J]. 清华大学学报:自然科学版, 2008, 28(11 ): 11931-1934. HUANG Wei-feng,LI Yong,LIU Qiu-sheng, et al. Numerical Investigation of Wake Galloping of Suspension Bridge Cables [J]. Journal of Tsinghua University:Science and Technology Edition, 2008, 28(11):1931-1934. |
| [19] | JTG/TD60—01—2004,公路桥梁抗风设计规范[S] JTG/T D60—01—2004,Wind-resistant Design Specification for Highway Bridges [S]. |
| [20] | 谭红霞,陈政清. CFD在桥梁断面静力三分力系数计算中的应用 [J]. 工程力学, 2009, 26(11): 68-72. TAN Hong-xia, CHEN Zheng-qing. Application of CFD in Calculating Static Coefficients of Bridge Section [J]. Engineering Mechanics, 2009, 26(11): 68-72. |
| [21] | LAM K, LI J Y,SO R M C. Force Coefficients and Strouhal Numbers of Four Cylinders in Cross Flow [J]. Journal of Fluids and Structures, 2003, 18(3): 305-324. |
| [22] | SIMIU E, SCANLAN R H. Wind Effects on Structures: An Introduction to Wind Engineering [M]. New York:John Wiley, 1986. |
| [23] | 徐枫, 欧进萍. 正三角形排列三圆柱绕流与涡致振动数值模拟 [J]. 空气动力学学报, 2010, 28(5): 582-590. XU Feng,OU Jin-ping, Numerical Simulation of Vortex-induced Vibration of Three Cylinders Subjected to a Cross Flow in Equilateral Arrangement [J]. Acta Aerodynamica Sinica, 2010, 28(5): 582-590. |
 2015, Vol. 31
2015, Vol. 31
