扩展功能
文章信息
- 王常峰, 包仪军, 陈兴冲, 丁明波
- WANG Chang-feng, BAO Yi-jun, CHEN Xing-chong, DING Ming-bo
- 活动支座状态对桥梁弹塑性地震反应的影响
- Effect of State of Movable Support on Elasto-plastic Seismic Response of Bridges
- 公路交通科技, 2015, Vol. 31 (3): 75-81
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 75-81
- 10.3969/j.issn.1002-0268.2015.03.013
-
文章历史
- 收稿日期:2014-06-16
2. 兰州交通大学 土木工程学院, 甘肃 兰州 730070
2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China
地震过程中支座的状态对桥梁结构的地震反应有很大影响,支座是地震中容易发生损坏的构件之一。地震震害表明,若固定支座发生破坏,则桥墩的震害较轻。近年来学者对支座的有限元分析模型进行了大量的研究,针对支座正常工作状态下的研究较多,而对支座破坏后的状态及其对桥梁抗震性能影响的研究较少。Sang-Hyo[1]将进入破坏状态的固定支座模拟成滑动单元,利用该单元对多跨简支梁桥的地震反应进行了研究,指出发生落梁震害的原因是设计时未考虑固定支座的剪切破坏。范立础[2]采用双向滑动支座模型对城市立交桥板式橡胶支座抗滑性能不满足要求、发生滑动时的动力性能进行了分析,通过对单墩模型和一条全线简支梁实际结构的分析,得出了板式橡胶支座发生滑动时动力特性的规律以及对结构的影响。李冲、王克海[3]为研究板式橡胶支座摩擦滑移后桥梁的抗震性能,通过拟静力试验,分析了支座摩擦滑移前后的滞回曲线、骨架曲线、支座变形、滑移位移、强度和刚度退化规律以及耗能能力等抗震性能指标。
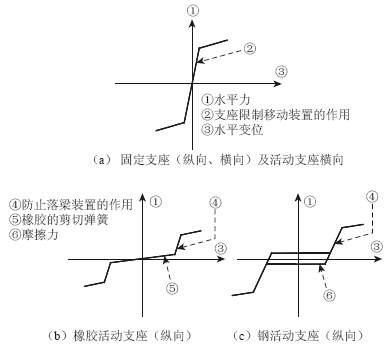
文献[4]规定对于桥梁上下部结构的支座连接部位应按照橡胶支座、钢支座和固定支座、活动支座的类型建立不同的有限元分析模型。另外,还必须考虑限位装置和防落梁装置的作用,还需要根据其构造材料考虑其材料非线性特性,其建议的支座连接部件的有限元模型如图 1所示。
|
| 图 1 支座连接部位有限元模型Fig. 1 Finite element models of support connection parts |
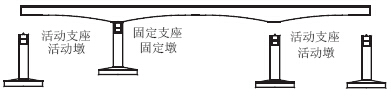
图 2为连续梁桥纵向抗震设计时计算惯性力的振动单元分配图,对于连续梁桥,在支座不破坏且活动支座滑动功能良好的情况下,一般认为连续梁桥的惯性力全部作用在固定支座墩(以下简称固定墩)上,固定墩发生破坏的可能性较大,而活动支座墩(以下简称活动墩)仅承受墩顶摩擦力的作用,发生破坏的可能性较小,故固定墩抵抗纵向地震作用的钢筋一般较活动墩多。
|
| 图 2 连续梁桥惯性力分配图Fig. 2 Inertial force distribution diagram of continuous beam bridge |
在阪神地震中,很多公路桥和铁路桥受到了严重破坏[5],在统计的17座桥墩严重破坏的3跨连续梁桥中,其中有7座桥仅固定墩发生破坏,有2座桥仅活动墩发生破坏,有8座桥固定墩和活动墩均发生了破坏。调查发现部分活动支座在地震过程中发生了破坏,使得活动墩承担的地震作用超出了设计分析的作用值,造成活动墩的破坏。故需要对活动支座在地震过程中的不同状态进行研究,并研究其对桥梁结构非线性地震反应的影响。 1 活动支座单元模型
活动支座的有限元模型对连续梁桥的非线性地震反应的影响较大,活动支座对结构的作用有[6]:① 活动支座滑动前具有一定的刚度,对桥梁整体刚度有一定的贡献,从而影响结构的自振特性和地震动输入能量;② 活动支座滑动后有一定的耗能作用,由于摩擦力的存在使得活动墩承担一定的地震作用;③ 活动支座达到其最大活动范围后,若丧失滑动功能使其活动范围有限,则对全桥的弹塑性地震反应有较大的影响。
为分析支座的工作状态对桥梁结构非线性地震反应的影响,采用3种支座模型模拟活动支座的作用。
(1) 支座模型一
支座模型一基于图 2假设,忽略活动支座的摩擦作用,活动墩与梁部结构采用竖向自由度耦合的方式连接,其他自由度均相互独立,梁体的全部惯性力作用在固定墩上,活动墩仅承担自身的惯性作用力。
(2) 支座模型二
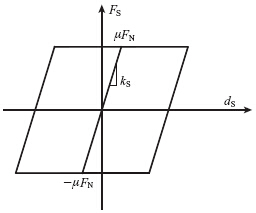
支座模型二基于库伦摩擦理论,将活动支座简化为理想弹塑性模型[2, 7, 8],考虑活动支座的摩擦力作用。对于常见的支座,其非线性大都可以简化为图 3所示的双线性模型。活动支座的竖向反力为FN,水平剪力为FS,剪切变形为dS,kS为活动支座初始剪切刚度,在活动支座发生滑动后剪切刚度取0,μ为支座接触面的滑动摩擦系数,临界滑动力FS=μFN。
|
| 图 3 摩擦单元力-位移曲线Fig. 3 Force-displacement curve of friction element |
(3) 支座模型三
支座模型三为活动范围受限的单元模型。当活动支座发生一定的位移后丧失滑动能力,造成活动支座两方向的活动范围受限,梁体若继续运动则会通过限制支座位移的破坏位置与桥墩发生碰撞,此时的支座位置处的连接模型应为支座摩擦单元(理想弹塑性模型)与位移锁定单元的组合。
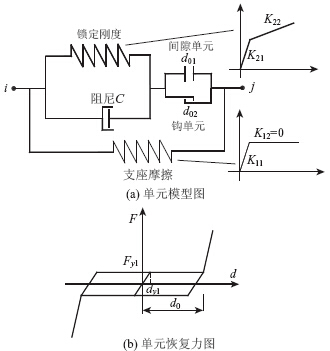
由于地震为往复运动,正负两方向的位移均可能受限,故需要采用间隙单元限制单元的正向位移[9, 10, 11],使用钩单元限制单元的负向位移,单元模型如图 4所示[12]。d01为单元正向可活动的范围,d02为单元负向可活动的范围,单元可活动范围为-d02~d01。K11为支座的初始刚度,K12为支座滑动后的刚度,Fy1,dy1为活动支座发生滑动的临界力和位移。K21为锁定装置的初始刚度,K22为锁定装置发生屈服后的刚度。支座活动范围取0可模拟活动支座在震动开始时就失去滑动能力的情况。
|
| 图 4 活动范围受限的支座有限元模型Fig. 4 Finite element model of movable support with limited movable range |
限制正向移动的接触单元的非线性力-变形关系为:
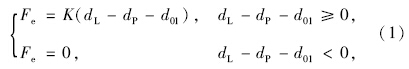
限制负向移动的钩单元的非线性力-变形关系为:
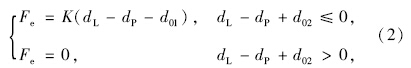
2 桥梁有限元分析模型
为研究活动支座的不同状态对桥梁结构非线性地震反应的影响,需建立全桥有限元模型进行分析,分析仅考虑纵桥向地震反应故采用平面有限元模型。地震过程中不考虑梁部结构的破坏,梁利用弹性平面梁单元模拟。桥墩非线性采用具有武田三线性滞回规律的梁单元模拟。塑性铰长度取1.0D(D为计算方向截面高度),塑性铰设置在墩底部,仅在塑性铰范围内考虑墩部结构的弹塑性。固定支座采用墩梁自由度耦合的方式进行模拟。将地基及桩基础对结构的作用简化成转动弹簧施加在承台底,地基系数的比例系数取20000 kPa/m2,弹簧刚度按照“m”法计算。
根据采用的3种不同的支座模型,全桥有限元分析模型也相应的分为如下3个模型[13]:
(1) 模型一:活动支座采用支座模型一模拟,利用主从自由度模拟,不考虑活动支座的作用,忽略活动支座的摩擦力。
(2) 模型二:活动支座采用支座模型二模拟,考虑活动支座的摩擦耗能作用,支座活动范围不受限,取活动支座的摩擦系数为0.02,0.05,0.10,0.15和0.20。由于支座发生滑动前的刚度一般较大,在分析中,中活动支座初始刚度取为1.0×106 kN/m,边活动支座初始刚度取为4.0×105 kN/m。
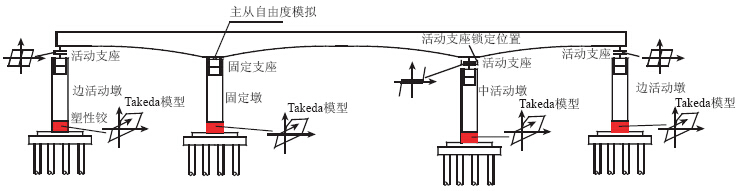
(3)模型三:中活动支座采用支座模型三模拟,边支座仅考虑活动支座摩擦作用,不考虑边支座的破坏,模型三计算模型如图 5所示。支座锁定刚度取1×106 kN/m,活动支座初始活动范围取-0.10~0.10 m。
|
| 图 5 模型三计算简图Fig. 5 Calculation diagram of model 3 |
以一座3跨连续梁桥作为算例,墩高20 m,桥墩为矩形截面,边墩截面尺寸为6.75 m×2.8 m,中墩尺寸为6.8 m×4.0 m。梁体为箱形梁,单箱单室直腹板变截面箱梁,梁体总重14 367.248 t,边支座竖向反力为8 793.74 kN,中支座竖向反力为63 042.5 kN。
针对目前不少桥梁存在活动墩配筋较少的情况,固定墩和活动墩采用不同的配筋率计算截面的弯矩-曲率曲线,对于固定墩取1%的配筋率,中活动墩取5种不同的配筋率,对该配筋截面进行M-φ全过程分析,可得出固定墩和中活动墩的墩底截面弯矩曲率骨架数据如表 1所示。
|
配筋率/ % |
开裂弯矩/ (kN·m) |
开裂曲率/ (rad·m-1) |
屈服弯矩/ (kN·m) |
屈服曲率/ (rad·m-1) |
极限弯矩/ (kN·m) |
极限曲率/ (rad·m-1) |
| 1 | 115 662 | 0.000 12 | 290 448 | 0.000 66 | 346 729 | 0.007 93 |
| 0.75 | 109 295 | 0.000 12 | 247 978 | 0.000 64 | 293 293 | 0.008 08 |
| 0.50 | 102 912 | 0.000 12 | 201 152 | 0.000 63 | 239 451 | 0.00 823 |
| 0.25 | 96 510 | 0.000 12 | 157 219 | 0.000 61 | 185 395 | 0.008 41 |
| 0.10 | 93 358 | 0.000 12 | 135 875 | 0.000 59 | 158 214 | 0.008 52 |
对上述有限元分析模型输入天津波和人工地震波,地震波峰值调整到0.4g,输入方向为桥梁纵向。人工地震波和天津波的反应谱如图 6所示。采用NEWMARK-β法进行非线性时程分析。

|
| 图 6 输入地震波的反应谱Fig. 6 Response spectra of input seismic waves |
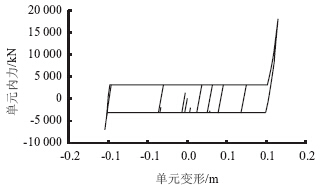
支座活动范围受限后,墩梁间连接单元由支座摩擦单元和位移锁定装置组成,活动支座摩擦系数为0.05,活动范围取±10 cm情况下的模型三单元滞回曲线如图 7所示[14]。
|
| 图 7 活动范围受限的活动支座单元滞回曲线Fig. 7 Hysteresis curve of movable support element with limited movable range |
由图 7可以看出,支座在达到其最大活动范围后,与锁定装置发生接触,由梁经过活动受限的活动支座传递到桥墩的地震作用将增大,从而影响到桥梁结构的地震反应。 4.2 墩底延性率
桥墩的延性率是控制桥墩破坏的一个重要指标,取固定墩和中活动墩底的最大地震反应进行分析,最大曲率φmax与桥墩屈服曲率φy的比值即为延性率μ:

天津波作用下模型一、二的最大曲率延性率如图 8(a)、(b)所示,人工波作用下模型一、二的最大曲率延性率如图 8(c)、(d)所示。

|
| 图 8 模型一、二最大曲率延性率Fig. 8 Maximum curvature ductility ratios of model 1 and model 2 |
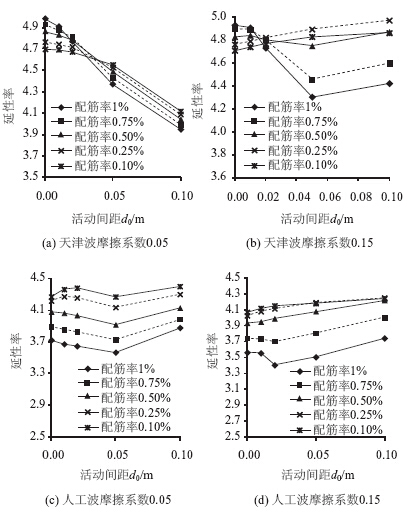
模型三天津波作用下固定墩最大曲率延性率如图 9(a)、(b)所示,人工波作用下固定墩最大曲率延性率如图 9(c)、(d)所示。
|
| 图 9 模型三固定墩底最大曲率延性率Fig. 9 Maximum curvature ductility ratios of fixed pier in model 3 |
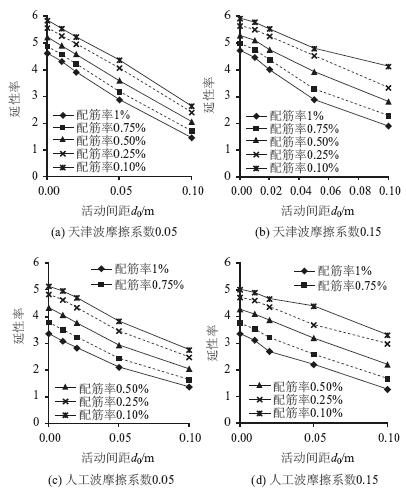
模型三天津波作用下中活动墩最大曲率延性率如图 10(a)、(b)所示,人工波作用下中活动墩最大曲率延性率如图 10(c)、(d)所示。
|
| 图 10 模型三中活动墩底最大曲率延性率Fig. 10 Maximum curvature ductility ratios of middle movable pier in model 3 |
从图 8~图 10可以看出:
(1) 考虑活动支座的摩擦作用后,人工波作用下的固定墩底曲率反应降低,而天津波作用下的固定墩底曲率增加,且随着摩擦系数的提高而增加;故活动支座的摩擦作用在某些情况下起到不利的影响,在连续梁桥的抗震设计时应计入活动支座摩擦作用的影响。
(2) 考虑活动支座摩擦作用后,相对于模型一的仅墩身惯性作用,活动墩顶增加了摩擦力的作用,故在天津波和人工波作用下模型二中活动墩底曲率均较模型一大,且随着支座摩擦系数即摩擦力的增大而增加。
(3) 模型三中活动墩活动范围受限后,梁体的惯性作用会对中活动墩产生较大的碰撞作用力,发生碰撞接触后梁与中活动墩同方向运动,使得中活动墩受力较大,且随着活动范围的减小,梁的惯性作用传递给中活动墩的作用力增大;在活动支座活动范围较小的情况下,模型三中活动墩可能会出现曲率延性率也较大的情况,中活动墩墩底曲率延性率随着活动范围的减小、配筋率的降低而增加;若活动支座在地震前已失去滑动能力即中活动间距为0的情况,中活动墩的墩底曲率可能较固定墩大。
(4) 对于固定墩,当活动支座的移动范围受限后,在人工波作用下,模型三墩底最大曲率反应小于模型二,说明在人工波作用下中活动墩地震反应的增加降低了固定墩的负担;但在天津波作用下,随着活动范围的减小,固定墩的墩底曲率反应反而增大,说明不同地震波的激励活动支座滑动范围受限对固定墩地震反应的影响并无一致的规律可循,固定墩底曲率反应受地震波的频谱特性的影响较大。
(5) 活动支座完全失去滑动能力后,活动墩与固定墩共同承担地震作用,有可能造成活动墩的破坏,故在设计时对活动支座的滑动能力及其对活动墩地震反应的影响也应给予足够的重视,加强活动墩的配筋防止破坏。 4.3 墩顶加速度
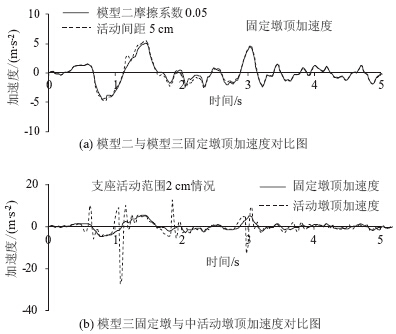
为研究中活动支座活动范围受限对梁体加速度和中活动墩顶加速度反应的影响,图 11列出了摩擦系数为0.05、中活动墩配筋率采用0.5%情况下的结构加速度时程反应,由于最大的加速度出现在地震动的初期,故仅列出前5 s的加速度时程反应。
|
| 图 11 加速度时程反应曲线Fig. 11 Time-history response curves of acceleration |
由图 11可以看出:
(1) 模型三固定墩顶加速度反应与模型二基本相近,在中活动墩与梁发生接触时刻,固定墩顶加速度较模型二大,其余时刻的加速度反应基本一致。
(2) 模型三由于梁体与中活动发生接触时的冲击作用,且由于中活动墩的固有振动周期较固定墩小许多,使得中活动墩顶的加速度反应较固定墩大,从而也影响到中活动墩底的最大曲率反应。 5 结论
针对活动支座活动范围受限情况下的连续梁桥活动墩的地震反应进行了研究,主要研究工作及结论如下:
(1) 针对地震中活动支座可能发生破坏的情况,构造了活动范围受限情况下的支座处连接单元的有限元模型。
(2)利用活动范围受限的支座连接处的有限单元模型建立了3种不同的模型,进行了非线性时程反应分析,结果表明,在支座活动范围受限甚至失去活动能力的情况下,活动墩承担的地震反应较常用抗震分析模型的设计结果增大许多,地震过程中也有可能发生破坏,在设计时对活动支座的滑动能力对活动墩地震反应的影响也应给予足够的重视。
(3) 支座连接处的状态对桥梁结构的地震反应有较大的影响,在有限元分析时,应考虑活动支座的不同状态精确模拟其作用,并考虑其可能产生的破坏对结构产生的不利影响。
| [1] | KIM S H, MHA H S, LEE S W. Effects of Bearing Damage upon Seismic Behaviors of a Multi-span Girder Bridge[J]. |
| [2] | 范立础,聂利英,李建中. 地震作用下板式橡胶支座滑动的动力性能分析[J]. 中国公路学报,2003,16(4):31-36. FAN Li-chu, NIE Li-ying, LI Jian-zhong. Dynamic Characteristic Analysis of Laminated Rubber Bearing Sliding under Earthquake [J]. China Journal of Highway and Transport, 2003, 16(4):31-36. |
| [3] | 李冲,王克海,李悦,等. 板式橡胶支座摩擦滑移抗震性能试验研究[J]. 东南大学学报:自然科学版, 2014,44(1):162-167. LI Chong, WANG Ke-hai, LI Yue,et al. Experimental Study on Seismic Performance of Laminated Rubber Bearings with Friction Slipping [J]. Journal of Southeast University: Natural Science Edition, 2014,44(1):162-167. |
| [4] | 日本铁道技术综合研究所.铁道构造物等设计标准同解说-耐震设计[S].东京:日本铁道技术综合研究所,2002. Japan Railway Technical Research Institute. Design Standards and Explanations for Railway Structures-Seismic Design[S].Tokyo: Japan Railway Technical Research Institute, 2002. |
| [5] | OTSUKA H, UNJOH S, TERAYAMA T, et al. Damage to Highway Bridges by 1995 Hyogoken Nanbu Earthquake and the Retrofit of Highway Bridges in Japan[C]//3rd US-Japan Workshop on Seismic Retrofit of Bridges. Osaka: [s.n.], 1996. |
| [6] | 王常峰,朱春林,陈兴冲. 活动支座摩擦作用对连续梁桥弹塑性地震反应的影响[J]. 公路交通科技, 2013,30(5):67-73. WANG Chang-feng, ZHU Chun-lin, CHEN Xing-chong. Effect of Friction Effect at Movable Support on Elasto-plastic Seismic Response of Continuous Girder Bridge [J]. Journal of Highway and Transportation Research and Development, 2013,30(5):67-73. |
| [7] | 聂利英,李建中,范立础. 滑动支座竖向动反力对桥梁结构动力性能的影响[J]. 同济大学学报:自然科学版,2002,30(11):1290-1294. NIE Li-ying, LI Jian-zhong, FAN Li-chu. Effects of Dynamic Vertical Resistance Force of Sliding Bearing of Bridges[J]. Journal of Tongji University: Natural Science Edition, 2002,30(11):1290-1294. |
| [8] | 叶爱君,胡世德,范立础. 桥梁支座抗震性能的模拟分析[J]. 同济大学学报:自然科学版,2001,29(1):6-9. YE Ai-jun, HU Shi-de, FAN Li-chu. Simulation of Seismic Behavior for Bridge Bearings[J]. Journal of Tongji University: Natural Science Edition, 2001, 29(1):6-9. |
| [9] | 许祥,鞠三,刘伟庆,等. 桥梁结构地震碰撞分析模型的碰撞刚度计算方法研究[J]. 振动与冲击,2013,32(12):31-39. XU Xiang, JU San, LIU Wei-qing, et al. Computation Methods for Impact Stiffness of Earthquake-induced Bridge Pounding Models [J]. Journal of Vibration and Shock, 2013,32(12):31-39. |
| [10] | 邓育林,彭天波,李建中. 地震作用下桥梁结构横向碰撞模型及参数分析[J]. 振动与冲击,2007,26(9):104-107,119,173-174. DENG Yu-lin, PENG Tian-bo, LI Jian-zhong. Pounding Model of Bridge Structures and Parameter Analysis under Transverse Earthquakes [J]. Journal of Vibration and Shock, 2007, 26(9):104-107,119,173-174. |
| [11] | 李建中,范立础. 非规则梁桥纵向地震反应及碰撞效应[J]. 土木工程学报, 2005, 38(1):84-90. LI Jian-zhong, FAN Li-chu. Longitudinal Seismic Response and Pounding Effects of Girder Bridges with Unconventional Configurations [J]. China Civil Engineering Journal, 2005, 38(1):84-90. |
| [12] | 王军文,李建中,范立础. 限位装置对连续梁桥地震反应的影响[J]. 铁道学报,2008,30(3):71-77. WANG Jun-wen, LI Jian-zhong, FAN Li-chu. Effects of Restrainers on Seismic Responses of Continuous Beam Bridges[J]. Journal of the China Railway Society, 2008, 30(3):71-77. |
| [13] | 康清,黄襄云,陈建秋,等. 多跨连续隔震桥梁的地震反应研究[J]. 地震工程与工程振动, 2014,34(1):217-223. KANG Qing, HUANG Xiang-yun, CHEN Jian-qiu,et al. Seismic Response Analysis of Multi-span Continuous Isolated Bridge [J]. Earthquake Engineering and Engineering Vibration, 2014,34(1):217-223. |
| [14] | 王常峰,陈兴冲,朱春林,等. 考虑支座及限位装置非线性的接触摩擦单元模型[J]. 工程力学,2013,30(8):186-192. WANG Chang-feng, CHEN Xing-chong, ZHU Chun-lin, et al. The Contact-and-friction Element Considering Nonlinear Performance of Movable Supports and Restrainers [J]. Engineering Mechanics, 2013,30(8):186-192. |
 2015, Vol. 31
2015, Vol. 31

 ,
,