扩展功能
文章信息
- 翟晓亮, 刘喆, 冯云成
- ZHAI Xiao-liang, LIU Zhe, FENG Yun-cheng
- 新月形拱-连续梁组合体系桥优化分析
- Analysis of Optimizing Crescent Arch and Continuous Girder Combination Bridge
- 公路交通科技, 2015, Vol. 31 (3): 68-74
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 68-74
- 10.3969/j.issn.1002-0268.2015.03.012
-
文章历史
- 收稿日期:2014-05-09
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710065
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710065, China
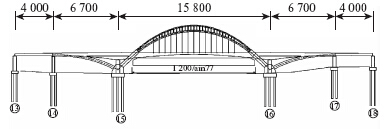
福建漳州市九龙江大桥主桥采用五跨预应力混凝土连续梁-钢管混凝土拱协作体系。主桥跨径组成为:(40+67+158+67+40)m,总长372 m。总体布置见图 1。
|
| 图 1 主桥总体布置(单位:cm)Fig. 1 General arrangement of main bridge (unit: cm) |
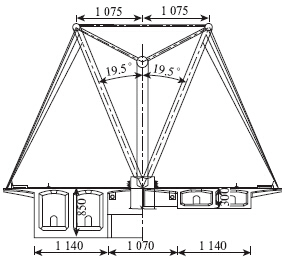
该桥由左右两幅预应力混凝土变截面连续梁和中间独立的中承式钢管混凝土拱3个受力体系组成。大桥以连续梁为受力主体,新月形钢管混凝土拱肋协助承担二期恒载、混凝土收缩徐变、温度变化、活载等作用[4, 5, 6]。每幅桥宽18.4 m,左右两幅连续梁桥桥间净距3.7 m,以便拱肋从中间穿过。两幅之间通过在主跨间的横梁连成一体,再由竖、斜吊杆悬吊横梁。新月形拱为横撑、斜撑和拱肋组成的空间倒三角形组合式结构。主拱肋采用直径1.8 m,钢管壁厚20 mm,内填C50微膨胀混凝土的钢管混凝土结构,位于桥梁中心线处的竖直平面内;副拱肋为直径1.2 m,钢管壁厚12 mm的空钢管结构,由竖直平面向两侧分别旋转19.5°。主梁预应力混凝土变截面连续梁,单幅采用单箱双室断面,箱梁顶板宽18.4 m,底板宽11.4 m,翼缘悬臂宽3.5 m。新月形钢管混凝土拱的主拱肋和副拱肋上均设置吊杆,主拱肋设竖吊杆,副拱肋设斜吊杆。竖吊杆的2对边吊杆采用15-25型,中吊杆采用15-19型,共15根;斜吊杆采用15-12型,共14根。在2个副拱肋之间共设置15道横撑,间距为6 m;在主拱肋与副拱肋之间共设置58道斜撑,间距为3 m。采用8根15-31环氧喷涂钢绞线可更换式成品系杆索。主桥典型横断面见图 2。
|
| 图 2 主梁典型横断面(单位:cm)Fig. 2 Typical cross-section of main girder(unit: cm) |
福建漳州九龙江大桥建设标准为一级公路(兼城市Ⅱ级主干道功能);桥梁宽度为主桥43 m,基本车道数为双向六车道,两侧设非机动车道、人行道;设计汽车荷载为公路-I级。
2 稳定性分析
单拱肋拱桥的面外刚度较弱,对于跨度较大的拱结构,如果拱截面弱轴的惯性矩较小,当作用在拱上的荷载达到临界荷载时,拱轴线在弯矩以及扭矩的作用下会向弱轴方向倾斜,发生拱的侧倾和侧向屈曲[5]。为获取影响新月形拱拱肋部分稳定性的控制因素,对主拱肋与副拱肋夹角、中吊杆与边吊杆布置、横撑和斜撑布置以及副拱肋4个方面进行了变参数分析。 2.1 主拱肋和副拱肋夹角
为研究主拱肋与副拱肋夹角对新月形拱整体稳定性的影响,保持主副拱肋结构尺寸与原设计一致按照15.5°,17.5°,19.5°,21.5°和23.5°这5种情况变化主拱肋与副拱肋在竖直平面内夹角,分别对5种情况下新月形拱-梁组合体系桥一类稳定进行计算,计算结果见表 1。
| 模态 | 夹角 | ||||
| 15.5° | 17.5° | 19.5° | 21.5° | 23.5° | |
| 1 | 6.58 | 6.54 | 6.48 | 6.41 | 6.32 |
| 2 | 8.43 | 8.39 | 8.33 | 8.26 | 8.18 |
| 3 | 12.07 | 12.02 | 11.96 | 11.90 | 11.83 |
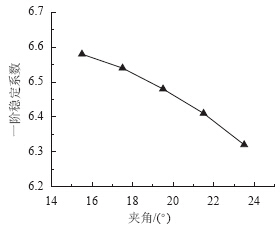
由于在实际工程中结构的第一阶失稳是最容易产生的,因其需要的能量最小,故我们对结构的低阶稳定要格外关注[6]。下面提取不同主副拱肋夹角对应的整体一阶稳定系数,如图 3所示。
|
| 图 3 主副拱夹角对稳定系数的影响Fig. 3 Influence of angle between main and side arch ribs on stability coefficient |
计算结果显示以上5种主副拱肋夹角对应的结构一阶失稳模态均为新月形拱侧向失稳,稳定系数均大于4,可见新月形拱-梁组合体系桥梁一类稳定性系数主要决定于新月形拱。由表 1和图 3可知,随着主拱肋与副拱肋夹角从15.5°变到23.5°,结构稳定系数逐渐减小。由于主拱与副拱形成了三角稳定体系,当主拱与副拱的夹角过大时,拱的横向刚度就会减小,进而对结构的整体稳定性不利。同时可以看出,随着主拱肋与副拱肋夹角变化,稳定系数减小程度很小。主副拱肋夹角受到桥面行车、行人净空要求的限制变化范围不大,可以认为主副拱肋夹角不控制新月形拱桥侧向稳定系数。因此在设计过程中主副拱肋夹角按照桥面净空要求及景观需要选择即可。 2.2 主拱竖吊杆和副拱斜吊杆
为研究主拱竖吊杆和副拱斜吊杆对新月形拱整体稳定性的影响,保持主副拱肋结构尺寸与原设计一致,按照3种工况分别对新月形拱-梁组合体系桥一类稳定系数进行计算。具体工况为:(1)保留全部竖吊杆和斜吊杆;(2)去掉所有竖吊杆仅保留斜吊杆;(3)去掉所有斜吊杆,计算结果见表 2。
| 荷载工况 | 一阶稳定系数 | 失稳形式 |
| (1) | 6.48 | 面外侧倾失稳 |
| (2) | 10.85 | 面外侧倾失稳 |
| (3) | 4.26 | 面外侧倾失稳 |
由表 2知,新月形拱侧向刚度较弱,3种工况下均为面外侧倾失稳;副拱斜吊杆对提高新月形拱的稳定性有利,主拱竖吊杆对稳定性提高不利。新月拱-连续梁组合体系桥梁的主梁相对于钢管拱可视为完全刚性,斜吊杆能有效约束拱平面内的水平位移,使拱的压力线偏心很小,与竖吊杆相比,斜吊杆在拱肋上的间距较大,有助于增加拱肋侧向稳定性。当拱肋有侧向位移时,斜吊杆的非保向力作用使得该类型桥梁的侧向稳定性有较大提高,因此斜吊杆对全桥的整体稳定性起重要作用。2.3 横撑和斜撑
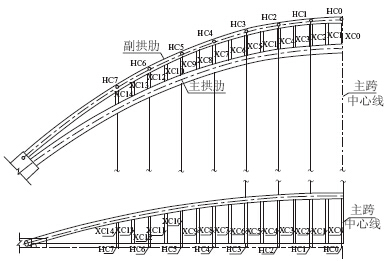
图 4为主副拱肋间横撑和斜撑布置图。为了研究主拱肋和副拱肋之间斜撑、副拱肋之间的横撑对新月形拱整体稳定性的影响,保持主副拱肋结构尺寸与原设计一致,按照以下3种工况分别对新月形拱-梁组合体系桥一类稳定系数进行计算。具体工况为:(1)保留全部横撑和斜撑;(2)去掉XC1-XC7和XC9-XC13,保留剩余斜撑及所有横撑;(3)去掉HC1-HC3和HC5-HC7,保留剩余横撑及所有斜撑,计算结果见表 3。
|
| 图 4 主副拱间横撑斜撑布置图Fig. 4 Layout of braces and sprags between main and side arch ribs |
| 荷载工况 | 一阶稳定系数 | 失稳形式 |
| (1) | 6.48 | 面外侧倾失稳 |
| (2) | 3.25 | 面外侧倾失稳 |
| (3) | 6.46 | 面外侧倾失稳 |
由表 3可知,新月拱-连续梁组合体系桥梁的拱肋斜撑对全桥整体稳定性贡献较大,横撑以及斜撑将主拱和副拱连接形成稳定的空间三角刚架,有效保证了全桥的整体稳定性。工况二稳定系数较小的原因是横撑连接的是2个副拱肋,主拱肋受到副拱肋的支撑急剧减小,侧向稳定系数大幅降低。
2.4 副拱肋
新月拱-连续梁组合体系桥梁的拱肋与一般拱桥的最大区别是,拱肋部分除主拱之外还有副拱存在,副拱肋对该类型桥梁的整体稳定性起了很大作用。通过分析设置副拱或取消副拱的条件下全桥整体稳定性,来确定副拱对全桥整体稳定性的贡献大小,计算结果见表 4。
| 模态 | 设置副拱 | 取消副拱 |
| 一阶 | 6.48 | 2.89 |
| 二阶 | 8.33 | 3.82 |
| 三阶 | 11.96 | 8.34 |
由表 4可知,副拱对于新月拱-连续梁组合体系桥梁的整体稳定性具有关键性的意义,九龙江大桥取消副拱后主拱肋稳定系数都不满足规范要求,可见副拱是影响新月形拱整体稳定性的关键因素。新月形拱-连续梁组合体系桥梁的副拱不仅有效保证了拱肋部分的整体稳定性,而且增加了拱肋的美感,提高了桥梁的景观价值。3 刚度分析
新月拱-连续梁组合体系桥由预应力混凝土连续梁承受自身全部恒载,新月拱通过吊杆协助承担二期恒载、混凝土收缩徐变产生的次内力及活载等其他运营阶段的荷载,采用系杆平衡两拱脚之间的水平推力,在受力特征上是典型的三元结构。拱和梁刚度对新月拱-连续梁组合体系桥梁设计有决定性作用,因此在确定桥梁形式后,可根据桥梁的传力方式和荷载在梁、拱中的不同分配比例,进行优化设计[7, 8, 9, 10]。通过分别调整拱肋和主梁抗弯刚度,分析恒载和活载作用下主拱拱顶、副拱拱顶、主梁跨中位置的内力和挠度变化规律,进一步研究新月形拱肋、主梁刚度变化对结构内力和刚度的影响程度。 3.1 主拱肋抗弯刚度
主拱肋取不同的抗弯刚度时,恒载、活载作用下结构产生的内力和挠度随主拱肋抗弯刚度变化规律如图 5~图 8所示。
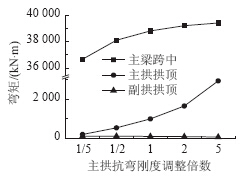
|
| 图 5 恒载作用下内力Fig. 5 Internal forces under action of dead load |
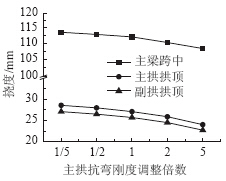
|
| 图 6 恒载作用下变形Fig. 6 Deformation under action of dead load |
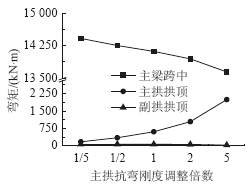
|
| 图 7 活载作用下内力Fig. 7 Internal force under action of live load |
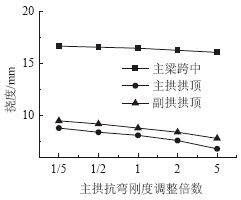
|
| 图 8 活载作用下变形Fig. 8 Deformation under action of live load |
恒载作用下结构产生的内力包含自重、二期和收缩徐变引起的内力,主拱肋除了承受自重之外还需协助预应力混凝土连续梁承担二期恒载和收缩徐变引起的内力。由图 5可知,恒载作用下主拱肋抗弯刚度增大5倍,主梁跨中弯矩增加约1.5%,主拱肋弯矩增大到约为原来的3倍,副拱肋弯矩减少约30%。主要原因是主拱肋刚度与主梁相比相对较小,主拱肋自重产生的内力也小,因此主拱肋分配的内力变化明显。由于主副拱肋之间通过横撑和斜撑连接为整体,主拱肋刚度增加,导致副拱肋分配的内力减小。由图 6可知,在恒载作用下随着主拱抗弯刚度不断增加主梁跨中的挠度、主拱和副拱挠度都有所减小。
由图 7和图 8可知,在活载作用下随着主拱抗弯刚度不断增加,拱梁跨中位置内力发生重新分配,主梁内力有所减少,主拱的内力有所增加。拱肋刚度增大5倍,主梁跨中位置弯矩减小约3.2%,拱肋弯矩增大约3.3倍,副拱肋弯矩减少到原来的50%。主拱肋刚度与主梁比相对较小,因此主拱肋刚度变化对主梁恒载内力影响不大,但对自身内力影响很大。由于主副拱肋之间通过横撑和斜撑连接为整体,主拱肋刚度增加,导致副拱肋分配的内力减小。 3.2 副拱肋抗弯刚度
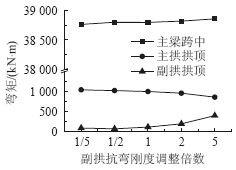
副拱肋取不同的抗弯刚度时,恒载、活载作用下结构产生的内力和挠度随副拱肋抗弯刚度变化规律如图 9~图 12所示。
|
| 图 9 恒载作用下内力Fig. 9 Internal force under action of dead load |
|
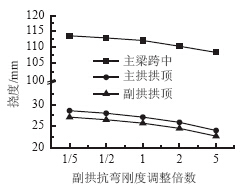
| 图 10 恒载作用下变形Fig. 10 Deformation under action of dead load |
|
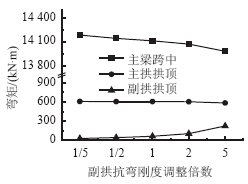
| 图 11 活载作用下内力Fig. 11 Internal force under action of live load |
|
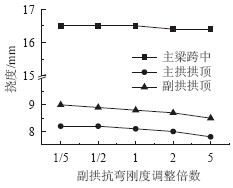
| 图 12 活载作用下变形Fig. 12 Deformation under action of live load |
由图 9和图 10可知,副拱肋刚度变化对主梁内力和变形几乎没有影响。副拱肋抗弯刚度增大5倍,主拱肋弯矩减小约15%,副拱肋弯矩增大到约为原来的3倍。主要原因是副拱肋刚度相对主梁过小,与主拱肋刚度相比副拱肋刚度也比较小。由图 10可知,在恒载作用下随着副拱抗弯刚度不断增加主梁跨中的挠度、主拱挠度几乎没有变化,主要原因还是副拱肋刚度与主梁、主拱肋刚度相比太小。
由图 11和图 12可知,在活载作用下随着副拱肋抗弯刚度增加,除了副拱肋自身分配到的内力值和变形变化明显外,主梁、主拱肋内力和变形变化均不明显。
3.3 主拱肋和副拱肋整体抗弯刚度
在原设计基础上同时调整主拱肋和副拱肋的抗弯刚度时,恒载、活载作用下结构产生的内力和挠度随主拱肋和副拱肋整体抗弯刚度变化规律如图 13~ 图 16所示。
|
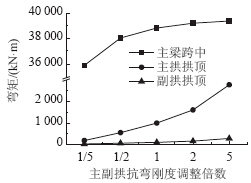
| 图 13 恒载作用下内力Fig. 13 Internal force under action of dead load |
|
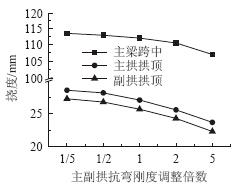
| 图 14 恒载作用下变形Fig. 14 Deformation under action of dead load |
|
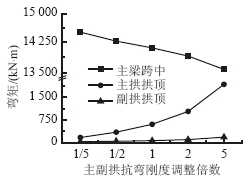
| 图 15 活载作用下内力Fig. 15 Internal force under action of live load |
|
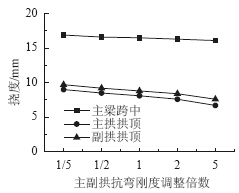
| 图 16 活载作用下变形Fig. 16 Deformation under action of live load |
由图 13和图 14可知,恒载作用下主拱肋、副拱肋抗弯刚度同时增大5倍,主梁跨中弯矩增加约1.5%,主拱肋弯矩增大到约为原来的2.8倍,副拱肋弯矩增大到约为原来的2.7倍,主梁跨中的挠度、主拱和副拱挠度都有所减小。与只增加主拱或副拱抗弯刚度相比,主梁内力几乎没有变化,主拱肋和副拱肋内力增大的程度略小于单独增大主拱肋或副拱肋刚度。
由图 15和图 16可知,活载作用下主拱肋、副拱肋抗弯刚度同时增大5倍,主梁跨中弯矩减小约3.7%,主拱肋弯矩增大到约为原来的3.2倍,副拱肋弯矩增大到约为原来的2.8倍,主梁跨中的挠度、主拱和副拱挠度都有所减小。与只增加主拱或副拱抗弯刚度相比,在活载作用下随着主拱和副拱抗弯刚度不断增加,主梁跨中弯矩减小程度增大。随着主拱肋和副拱肋整体抗弯刚度的提高,主拱肋和副拱肋将承担更多的活载,截面弯矩不断增加,有助于提高结构整体刚度。 3.4 主梁抗弯刚度
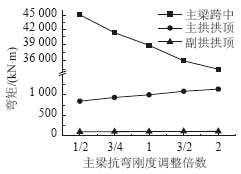
主梁整体抗弯刚度取不同值时,恒载、活载作用下结构产生的内力和挠度随主梁抗弯刚度变化规律如图 17~图 20所示。
|
| 图 17 恒载作用下内力Fig. 17 Internal force under action of dead load |
|
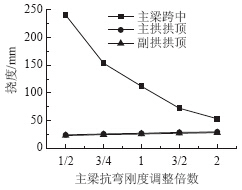
| 图 18 恒载作用下变形Fig. 18 Deformation under action of dead load |
|
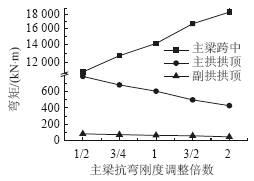
| 图 19 活载作用下内力Fig. 19 Internal force under action of live load |
|
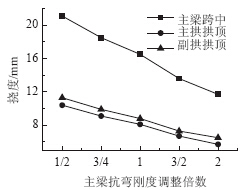
| 图 20 活载作用下变形Fig. 20 Deformation under action of live load |
由图 17和图 18可知,在恒载作用下,随着主梁抗弯刚度不断增加,主梁弯矩和挠度不断减小,由于新月拱相对于连续梁为柔性结构,荷载更多传递给新月拱,导致主拱和副拱拱顶内力和挠度均不断增大[11, 12]。
由图 19和图 20可知,在活载作用下,随着主梁抗弯刚度不断增加,连续梁相对于新月拱刚度更大,分配更多的荷载,导致主梁弯矩增大,主拱和副拱内力减小。主梁抗弯刚度增大有助于提高结构整体抗弯刚度,使结构变形减小。主梁刚度减小到约为原来的1/2,主梁跨中位置弯矩减少约27%,主拱肋和副拱肋拱顶弯矩增大到约为原来的1.3倍。 4 结论
(1)新月拱-连续梁组合体系桥的新月形拱是由主拱肋、副拱肋、横撑和斜撑组成的稳定的空间异型结构,具有灵活多变的空间造型,且能协助主梁承担部分二期恒载、混凝土收缩徐变、温度变化、活载等作用,实现了景观造型与结构受力的统一。
(2)新月形拱的稳定性决定该桥型的稳定性,副拱肋、连接主副拱肋的斜撑以及副吊杆对新月形拱的稳定性起关键作用,设计过程中需要高度重视;主副拱肋夹角对新月形拱的稳定性影响可以忽略,因此主副拱肋夹角按照桥面行车、行人净空需要和景观效果确定即可。
(3)恒载和活载分别作用下,新月形拱的主拱肋、副拱肋和主梁抗弯刚度对内力分配的影响规律是一致的,拱肋部分刚度越大,分配到的内力越大,主梁内力和变形减小的程度也越大;可以通过优化主梁和新月形拱肋之间的刚度比,确定一个造价兼顾景观最优的拱梁组合体系桥方案。
| [1] | 李映. 拱梁组合体系桥梁的拱梁相对刚度分析[J].桥梁建设, 2008(1):50-53. LI Ying. Analysis of Relative Rigidity of Arches and Beams of Arch and Beam Hybrid System Bridges [J]. Bridge Construction, 2008(1): 50-53. |
| [2] | 金成棣.预应力混凝土梁拱组合桥梁[M].北京:人民交通出版社,2001. JIN Cheng-di. Prestressed Concrete Girder and Arch Combination Bridge[M]. Beijing: China Communications Press,2001. |
| [3] | 汤少青.两种新月形拱-梁组合体系桥梁受力性能比较[J].中外公路,2013,33(8),175-178. TANG Shao-qing. Comparative Study on Structural Performance of Two Crescent Arch and Girder Combination Bridges[J]:China and Foreign Highway,2013,33(8): 175-178. |
| [4] | 冯云成.上承式预应力混凝土刚性梁柔性拱桥静力分析[J].世界桥梁,2012,40(1),47-49,64. FENG Yun-cheng. Analysis of Static Force of Prestressed Concrete Rigid Girder and Flexible Arch Deck Bridge [J]. World Bridges, 2012,40(1): 47-49,64. |
| [5] | 吴万忠,肖汝诚.下部结构刚度对梁拱组合桥静力性能的影响[J].公路交通科技, 2010,27(5):78-82. WU Wan-zhong,XIAO Ru-cheng. Influence of Substructure Stiffness on Static Performance of Arch-beam Composite Bridge [J].Journal of Highway and Transportation Research and Development, 2010,27(5):78-82. |
| [6] | 蔡金标,陈海浪,胡蒙.下承式3跨连续梁拱组合桥梁实用计算方法 [J].公路交通科技, 2011,28(1):62-67. CAI Jin-biao,CHEN Hai-lang,HU Meng. A Practical Computational Method for Three-span Continuous Beam-arch Through Bridge[J]. Journal of Highway and Transportation Research and Development, 2011,28(1):62-67. |
| [7] | 连岳泉,梁群.单拱肋外倾式钢管混凝土拱桥动力特性分析[J]. 武汉理工大学学报:交通科学与工程版,2012(10):984-987. LIAN Yue-quan,LIANG Qun. Dynamic Characteriscs Analysis of Extroversion CFST Arch Bridge with Single Rib[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering Edition,2012(10):984-987. |
| [8] | 朱小林.大跨径飞燕式钢管混凝土异型拱桥稳定性分析[D]. 长春:吉林大学,2011. ZHU Xiao-lin. Stability Analysis of Large Span"Fly-bird-type"Concrete Filled Steel Tube Arch Bridge with Special-shape[D]. Changchun:Jilin University, 2011. |
| [9] | 易云焜,往文杰.梁拱组合桥梁的拱梁荷载分担比例研究[J].桥梁建设, 2008(2):34-37. YI Yun-kun,WANG Wen-jie. Study of Load Sharing Ratio of Beam and Arch of Beam and Arch Hybrid Bridge[J]. Bridge Construction, 2008(2): 34-37. |
| [10] | 刘宇闻, 傅少君, 瞿国钊. V形刚构-拱组合桥静力有限元分析[J].公路交通科技, 2010,27(10):66-71. HLIU Yu-wen,FU Shao-jun,ZHAI Guo-zhao. Static Finite Element Analysis of Arch Bridge with V-shaped Rigid-frame[J]. Journal of Highway and Transportation Research and Development, 2010,27(10): 66-71. |
| [11] | JTG D62—2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004,Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [12] | JTG D62—2004,公路桥涵设计通用规范[S]. JTG D62—2004,General Code for Design of Highway Bridges and Culverts[S]. |
 2015, Vol. 31
2015, Vol. 31

 ,
,