扩展功能
文章信息
- 左一泽, 刘玉擎, 蔺钊飞
- ZUO Yi-ze, LIU Yu-qing, LIN Zhao-fei
- 槽型双箱组合梁斜拉桥桥面板有效宽度分析
- Study on Effective Width of Deck in Twin-box Groove Composite Girder Cable-stayed Bridge
- 公路交通科技, 2015, Vol. 31 (3): 63-67
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 63-67
- 10.3969/j.issn.1002-0268.2015.03.011
-
文章历史
- 收稿日期:2014-05-20
槽型双箱组合梁斜拉桥兼具槽型单箱组合梁与矩形双箱组合梁的优点,同槽型单箱组合梁相比,省去了大部分的钢底板,减少了钢材用量、制作与加工费用;同矩形双箱组合梁相比,其钢箱横桥向宽度大,具有较大的横向抗弯刚度,混凝土桥面有效分布宽度更大,近些年在国内外斜拉桥建设中逐渐得到应用[1]。
组合梁斜拉桥的主梁由混凝土桥面板和钢梁通过连接件结合而成,斜拉索通常锚固在钢梁上。在主梁辅助墩顶、辅助跨和中跨跨中等部位,由于拉索水平力的累加值较小或存在较大负弯矩和拉力,需要配置一定量的预应力筋防止混凝土开裂。预应力筋在锚固点附近产生较大局部应力,沿桥面板传递一定距离后逐渐扩散至整个桥面,导致一定范围内桥面板正应力横向分布不均匀[2]。
AASHTO LRFD(2007)[3]规范中对双主梁斜拉桥有效翼缘宽度进行了规定,即预应力效应和法向力沿主梁的两侧以30°的角度向桥面板及翼缘板传递,并逐渐均匀分布在整个桥面上,位于2个夹角之间的有效翼缘宽度也由小变大,直至整个截面参与工作。DIN 1075[4]规范规定双主梁断面在纵向集中力作用下的有效翼缘宽度,沿主梁的两侧以26.5°的角度向桥面板及翼缘板传递,并逐渐均匀分布在整个桥面。我国现有规范关于桥面板有效宽度的计算主要针对简支梁桥和连续梁桥,对组合梁斜拉桥桥面板有效宽度的规定尚不完善,而组合梁斜拉桥主梁为压弯构件,其桥面板有效宽度问题存在不同于梁桥的特点。
以往研究多通过建立有限元节段模型对双工型钢截面主梁型式组合梁斜拉桥不同工况下桥面板有效宽度进行研究[5, 6, 7, 8],而对预应力作用下双箱槽型组合梁斜拉桥的桥面板有效宽度的研究则相对缺乏。此外,既往的研究认为桥面板的有效宽度沿力作用点两侧按恒定轴向力扩散角传递至整个截面[9, 10],这对初始线性段是适用的,但并不能反映之后的应力传递规律的变化。为此,针对槽型双箱组合梁斜拉桥,研究其在纵向预应力作用下的应力分布特点,提出了预应力传递角度变化的桥面板有效宽度的计算方法,为同类组合梁斜拉桥设计提供参考。 1 有限元计算模型
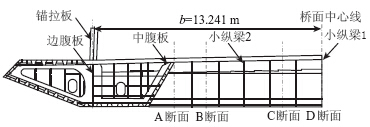
某大跨度斜拉桥主梁采用槽型双箱组合梁加纵横梁体系(图 1),桥面板在锚拉板之间区域为混凝土桥面板,两侧为钢桥面,桥面全宽37 m(含风嘴),纵向每隔4.5 m设一道实腹式横隔板,实腹式横隔板之间设置空腹式横隔板,桥面中心处梁高3.0 m。
|
| 图 1 槽型双箱组合梁截面构造Fig. 1 Section details of double-box groove composite girder |
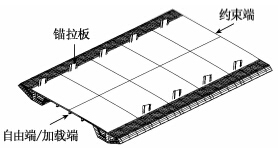
取斜拉桥5个标准梁段共45 m进行有限元分析,有限元模型如图 2所示。混凝土和钢板分别采用实体和板壳单元模拟,焊钉连接件采用三维弹簧单元模拟,在钢-混结合面采用接触单元模拟其相互作用。钢材为桥梁结构用钢Q345qD,弹性模量为2.1×105 MPa,泊松比为0.3;混凝土采用C60混凝土,弹性模量3.6×104 MPa,泊松比0.19。焊钉连接件直径为22 mm,高度为200 mm。焊钉连接件剪切刚度取为420 kN/mm[11]。桥面板轴向力采用等效节点荷载施加。计算过程为了避免其他因素的影响,没有计入自重效应。
|
| 图 2 标准梁段有限元计算模型Fig. 2 FE model of standard beam segment |
考虑到实桥预应力筋一般沿横桥向对称布置,为此选取一半宽度的桥面进行分析。在节段模型的一端施加三向平动约束,在另一端施加荷载。纵向预应力作用采用集中力施加于混凝土桥面板不同横向断面位置上,且对称于横桥向中心线。A断面为距离桥面中心线8.553 m的中腹板断面;B断面为半幅混凝土桥面板的中心位置;C断面为位于两小纵梁中点处的断面,距离中心线为2.25 m;D断面为桥面中心线位置。
在以下研究中,将有效宽度系数η作为衡量有效宽度的指标:

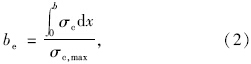
2 预应力作用下有效宽度影响因素分析 2.1 顺桥向加载位置对有效宽度的影响
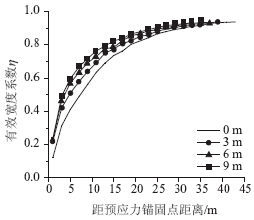
图 3为在距梁端自由端不同顺桥向距离处加载时的桥面有效宽度系数分布。在梁端自由端加载时,桥面有效宽度系数最小,且随着预应力锚固点距自由端距离的增加。在距加载点相同顺桥向距离的桥面板有效宽度系数不断增大,但当锚固点距自由端的距离达到6 m后,距锚固点相同距离处的桥面有效宽度系数增大程度很小。而且顺桥向锚固位置距梁端自由端越远,有效宽度初始发展越快,最后趋于稳定。为此,为了研究的一般性,且偏安全考虑,以下加载均在梁端自由端加载。
|
|
图 3 顺桥向加载位置对有效宽度系数影响Fig. 3 Effect of longitudinal loading position on effective width coefficient |
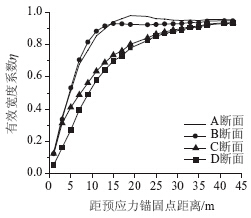
横向加载位置对有效宽度系数的影响,如图 4所示。当预应力作用于半幅桥面板中线处B断面时,轴向力沿B断面两侧对称传递至整个桥面。在距预应力锚固点相同距离处,桥面有效宽度系数为A~D各断面加载中最大。当预应力作用于桥面中心线处D断面时,应力仅沿一侧传递至整个桥面,在距预应力锚固点相同距离处桥面有效宽度系数最小,需要更长的距离将应力扩散至整个断面。当预应力作用于A,C断面时,有效宽度系数介于B,D断面之间,初始段有效宽度系数变化与B断面加载相似,后半段逐渐更相似于D断面加载。为了研究的普适性,以下加载均在C断面加载。
|
| 图 4 横桥向加载位置时有效宽度系数影响Fig. 4 Effect of lateral loading position on effective width coefficient |
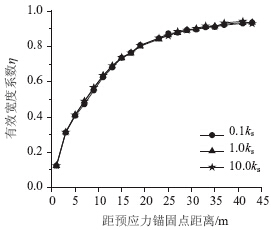
钢-混结合面连接件刚度对保证钢梁与混凝土桥面板组合作用的发挥及全桥的刚度和受力至关重要,为研究连接刚度ks对有效宽度系数的影响,分别计算0.1ks,1.0ks,10.0ks情况下在C断面加载时桥面板有效宽度系数,如图 5所示。可知连接件刚度变化对桥面板有效宽度系数几乎无影响,设计时可忽略其影响。
|
| 图 5 焊钉刚度对有效宽度系数影响Fig. 5 Effect of stud connector stiffness on effective width coefficient |
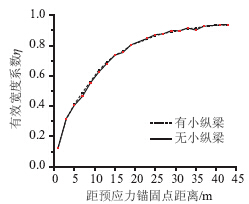
分别计算了主梁截面有无小纵梁两种情况下的桥面有效宽度系数,如图 6所示。无小纵梁情况采用中杀死小纵梁单元,并删除其结合面上的接触和连接件的方法进行模拟。小纵梁对桥面板的有效宽度提高幅度有限,几乎无影响。因此,在设计计算桥面板有效宽度时可以忽略小纵梁参与结构作用,计算结果偏安全。
|
| 图 6 小纵梁对有效宽度系数分布Fig. 6 Distribution of effective width coefficients in little longitudinal girder |
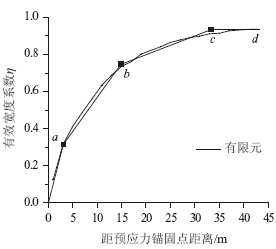
为分析的一般性,选取C断面加载进行分析。断面加载对应的有效宽度系数曲线,如图 7所示。初始时有效宽度系数近似线性增加至a点,对应变化率为k1;当超过a点,曲线变化率发生明显改变,并近似线性增加至b点,对应变化率为k2;当超过b点,曲线变化率再次发生明显改变,并近似线性增加至c点达到最大有效宽度系数,对应变化率为k3;当超过c点,有效宽度系数大于0.9时,增长速度减缓,对应变化率为k4。
|
| 图 7 断面C有效宽度系数发展趋势Fig. 7 Development trend of effective width coefficient of section C |
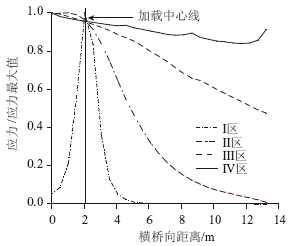
图 8所示为o~a(Ⅰ区),a~b(Ⅱ区),b~c(Ⅲ区)和c~d(Ⅳ区)4个区域内正应力横向分布。为便于比较,通过将同一断面应力除以该断面最大应力进行无量纲化。Ⅰ区内,应力沿加载点两侧对称传递,应力最大点位于加载点位置,近似于钟形分布,有效宽度系数增加较快;Ⅱ区内,应力最大点向桥面中心转移,且横桥向应力分布不再呈现沿加载点的对称性,离中心较近一侧应力分布已较为均匀,另一侧仍近似呈钟形分布;Ⅲ区内,应力最大点转移至桥面中心处,且横桥向应力分布近似为线性,但横向分布仍较为不均匀;Ⅳ区内,横桥向应力分布依然近似为线性,但应力已较为均匀。基于正应力横向分布特点可知,有效宽度曲线可近似为四折线形式。
|
| 图 8 不同顺桥向区域的桥面板截面正应力横向分布图Fig. 8 Transverse distributions of normal stresses in deck slab section in different longitudinal areas |
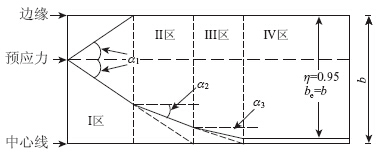
预应力作用下桥面板应力传递规律如图 9所示,Ⅰ区内预应力以初始轴力传递角α1沿锚固点两侧传递,应力呈钟形分布,对应全截面有效宽度系数变化率k1=2tanα1。当应力传递至距锚固点较近的桥面板边缘时,进入Ⅱ区,此时传递至边缘一侧的应力停止横向传递,不再呈钟形分布,另一侧依然呈钟形分布,保持变化率tanα1,对应全截面有效宽度系数变化率为k2=tanα2。当应力传递至距锚固点较远边界时,进入Ⅲ区,两侧均停止横向传递,应力分布近似呈线性,在截面内部继续调整,对应全断面有效宽度系数变化率为k3=tanα3;随着应力在横向逐渐趋于均匀,并达到稳定,进入Ⅳ区,对应全断面有效宽度系数变化率为k4=0。其中,α反映整个过程轴向力在混凝土桥面板中的传递角度。
|
| 图 9 预应力作用下桥面板应力传递规律Fig. 9 Stress transferring rule of deck slab under action of prestress |
因此,可认为组合梁在预应力作用下混凝土桥面板内应力在锚固点两侧沿一定角度传递,且传递角度随传递距离发生变化。通过对各个断面加载对应有效宽度系数曲线进行数值拟合,得到在本文的边界条件下,轴力传递角α1取33.5°,α2取23°,α3取10°,最大有效宽度系数取0.95时最优。 3.3 有效宽度系数计算方法对比
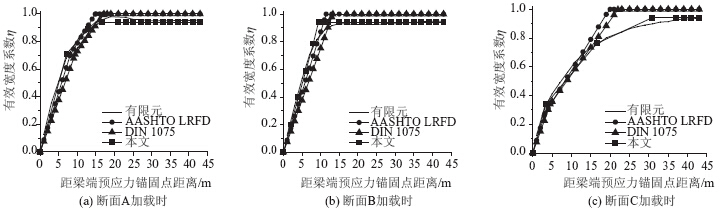
将本文提出的有效宽度系数计算方法与AASHTO LRFD(2007)和DIN 1075所建议方法进行对比,结果如图 10所示。可见,与两种规范相比,本文的计算方法更适于槽型双箱钢-混组合梁在预应力作用下有效宽度系数的计算,能够较为全面地反映实际应力分布和有效宽度系数的变化特点。
|
| 图 10 加载时桥面板有效宽度系数分布Fig. 10 Distributions of effective width coefficients under loading |
(1)提高组合梁连接件刚度和设置小纵梁有利于提高桥面整体刚度,但对桥面板有效宽度系数提高幅度有限,设计过程中可忽略其影响。
(2)预应力作用下,顺桥向锚固位置距梁端自由端越远,有效宽度系数增长越快,但当远离自由端一定距离后,影响趋于稳定,有效宽度系数增长速率不再变化。而现有有效宽度计算方法按自由端加载计算,偏于保守。
(3)在预应力作用下,存在初始轴力传递角,当轴向力按此角度传递至桥面板任一侧边缘时,应力分布规律将发生改变,对应轴向力传递角度亦将发生变化,当两侧按此初始轴力传递角度均传递至边缘时,轴向力传递角不再发生变化,有效宽度以此角度逐渐发展,并最终达到最大桥面板有效宽度系数0.95。
(4)相对于AASHTO LRFD(2007)和DIN 1075,本文提出的有效宽度计算方法能够考虑轴向力在桥面板中传递的全过程特点及轴向力传递角度的变化,计算结果较为符合混凝土桥面板内实际应力分布情况,可为同类组合梁斜拉桥设计提供参考。
| [1] | 罗杰, 刘玉擎. 大跨径斜拉桥组合梁结构体系与构造[C]//2010大跨径桥梁创新技术论坛论文集.北京:人民交通出版社,2010. LUO Jie, LIU Yu-qing. Structural System and Structural Pattern of Long Span Composite Cable-stayed Bridge[C]//Proceedings of 2010 Innovative Technology Forum of Long Span Bridges. Beijing: China Communications Press,2010. |
| [2] | 张玉平, 李传习. 预应力对斜拉桥箱梁剪力滞效应的影响[J]. 世界桥梁, 2009 (4): 39-41,49. ZHANG Yu-ping, LI Chuan-xi. Influence of Prestressing Force on Shear Lag Effect of Box Girder of PC Cable-stayed Bridge[J]. World Bridges, 2009 (4): 39-41,49. |
| [3] | AASHTO LRFD-2007,AASHTO LRFD Bridge Design Specifications [S]. |
| [4] | DIN 1075—1981, Concrete Bridges-Dimensioning and Construction [S]. |
| [5] | 刘沐宇, 刘洋, 袁卫国. 考虑滑移效应的三塔结合梁斜拉桥桥面板有效宽度分析[J].武汉理工大学学报:交通科学与工程版, 2012, 36(5): 877-880. LIU Mu-yu, LIU Yang, YUAN Wei-guo. Study on Effective Width of Concrete Slab in Composite Cable-stayed Bridge Considering Slip Effect[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2012, 36(5): 877-880. |
| [6] | 戚冬艳, 于东民, 李文华,等. 大跨径跨海斜拉桥组合梁桥面板剪力滞效应[J]. 长安大学学报:自然科学版, 2013, 33(6):68-73. QI Dong-yan, YU Dong-min, LI Wen-hua, et al. Shear Lag Effect of Composite Beam Panel of Sea-crossing Cable-stayed Bridge with Large Span[J]. Journal of Chang'an University:Natural Science Edition, 2013, 33(6):68-73. |
| [7] | 颜娟, 黄才良. 双主梁式斜拉桥主梁有效宽度[J]. 长安大学学报:自然科学版, 2003, 23(1): 46-48. YAN Juan,HUANG Cai-liang. Efficient Width for Cable-stayed Bridge with Two Edge Girders[J]. Journal of Chang'an University:Natural Science Edition, 2003, 23(1): 46-48. |
| [8] | DEZI L, GARA F, LEONI G. Effective Slab Width in Prestressed Twin-girder Composite Decks[J]. |
| [9] | 周绪红, 狄谨, 戴公连. 大跨径预应力混凝土斜拉桥主梁节段模型的研究[J]. 土木工程学报, 2005, 38(3): 59-63. ZHOU Xu-hong, DI Jin, DAI Gong-lian. Study on Segmental Model of Girder of Long-span Prestressed Concrete Cable-stayed Bridge[J]. China Civil Engineering Journal, 2005, 38(3): 59-63. |
| [10] | 翟晓亮, 王春生, 冯云成,等. 组合梁斜拉桥有效宽度系数及实用计算方法[J]. 长安大学学报:自然科学版,2013, 33(1): 51-58. ZHAI Xiao-liang, WANG Chun-sheng, FENG Yun-cheng et al. Effective Width Coefficient for Composite Cable-stayed Bridge and Its Practical Calculation Method[J]. Journal of Chang'an University:Natural Science Edition,2013, 33(1): 51-58. |
| [11] | 蔺钊飞, 刘玉擎, 贺君. 焊钉连接件抗剪刚度计算方法研究[J]. 工程力学, 2014, 31(7):85-90. LIN Zhao-fei, LIU Yu-qing, HE Jun. Research on Calculation Method of Shear Stiffness for Headed Stud Connectors[J]. Engineering Mechanics, 2014, 31(7):85-90. |
 2015, Vol. 31
2015, Vol. 31

 ,
,