扩展功能
文章信息
- 高新文, 张艳聪, 高玲玲
- GAO Xin-wen, ZHANG Yan-cong, GAO Ling-ling
- 考虑传力杆位置偏差的刚性路面接缝传荷预估模型
- Joint Load-transfer Prediction Model of Rigid Pavement Considering Position Deviation of Dowel Bar
- 公路交通科技, 2015, Vol. 31 (3): 57-62
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 57-62
- 10.3969/j.issn.1002-0268.2015.03.010
-
文章历史
- 收稿日期:2013-10-16
2. 山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室, 山西 太原 030006;
3. 山西水利职业技术学院, 山西 运城 044004
2. Key Laboratory of Highway Construction & Maintenance in Loess Region, Shanxi Transport Research Institute, Taiyuan Shanxi 030006, China;
3. Shanxi Conservancy Technical College, Yuncheng Shanxi 044004, China
水泥混凝土面层被接缝分割成规则的矩形板块,板块间通过传力杆连接。接缝是路面结构最薄弱的部位,其传荷能力直接影响路面使用性能。传力杆设置时需保证杆端自由滑动,以利于混凝土面层的温度变形,同时满足剪力传递的需求,以保证荷载的板间转移。以往的研究中,多将路面结构等效为半空间地基或Winkler地基上的弹性薄板,并在此基础上计算标准轴载下传力杆正常工作时的力学特征。Zollinger[1]、Ioannides[2]、陈飞[3]、周正峰[4]、Guo Hua[5]等基于Winkler地基上的弹性薄板理论建立了水泥混凝土路面接缝传荷能力与接缝传荷刚度、路面结构参数和荷载之间的关系;周德云[6]采用Winkler地基假设和剪切弹簧单元模型作为接缝传荷介质,分析了接缝处的传荷能力,并建立了接缝挠度传荷系数与板边应力折减系数之间的相关关系。这些研究多未考虑实际工程中传力杆位置偏差的问题,也忽略了荷载级位对弯沉测试的影响。事实上,实际施工中传力杆经常出现位置偏差和功能损失[7, 8],处于非理想工作状态;传力杆水平偏角、竖直偏角和竖向位移均对接缝传荷能力有显著影响[9]。传荷能力还和测试荷载有关,弯沉测试时冲击荷载越小,弯沉传荷系数误差越大[10]。
鉴于此,本文在建立Winkler地基上考虑层间接触状况的等平面尺寸双层结构模型的基础上,考查传力杆空间位置偏差(水平偏角、竖直偏角、竖向位移)、弯沉测试荷载等因素对接缝传荷能力的影响,建立考虑传力杆实际位置偏差的接缝传荷能力预估模型,并基于FWD实测弯沉数据对预估模型进行修正。 1 接缝传荷能力的虚拟试验 1.1 试验方法
一般认为接缝传力杆主要传递剪力,接缝传荷模式由接缝剪切刚度表征,接缝的荷载传递能力及效率采用弯沉传荷系数LT和应力折减系数λσ表征,接缝剪切刚度,LT,λσ与传力杆空间位置、弯沉测试荷载、传力杆抗弯刚度及其和混凝土的结合状况有关[11]。本文采用弯沉传荷系数LT来评价接缝传荷能力:

在接缝处集料嵌锁状况相当的前提下,接缝弯沉传荷系数与传力杆实际空间位置(水平偏角、竖直偏角、埋深偏差)、弯沉测试荷载的大小、传力杆抗弯刚度及其和混凝土的结合状况有关,即弯沉传荷系数:
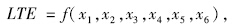
为统筹考量6个因素对弯沉传荷系数的贡献,依据现有弯沉测试条件并结合工程实际,首先做以下假定:(1)测试荷载相同;(2)传力杆抗弯刚度相同(直径32 mm、长度500 mm、模量200 GPa);(3)传力杆与混凝土结合状况相同(竖向支撑模量10 000 MPa,水平约束模量为0)。然后,通过数值试验逐一计算水平偏角x1、竖直偏角x2和竖向位移偏差x3对弯沉传荷系数LTE的影响,并采用多元非线性回归技术得到弯沉传荷系数预测模型f(x1,x2,x3)。
为准确获得车轮荷载单独作用下横缝两侧的实际弯沉,并方便与实测弯沉在等环境下进行比较,首先计算温度荷载和车轮荷载共同作用下的接缝处路面结构的弯沉,然后计算温度荷载单独作用下的弯沉,并最终得到车辆荷载单独作用下相应位置的弯沉值。
接缝处弯沉传荷系数的计算采用有限元方法进行,计算软件为Ever FE 2.25。 1.2 计算模型建立
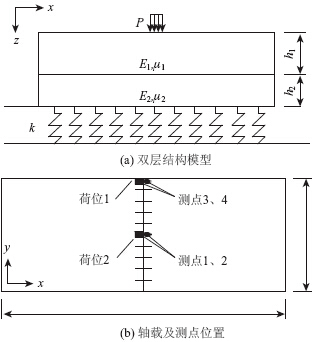
路面力学计算模型为Winkler地基上考虑层间接触状况的等平面尺寸双层结构模型,如图 1(a)所示,该模型可实现在考虑路面结构实际层间接触状态的前提下,考查传力杆位置偏差(水平偏角、竖直偏角和埋深偏差)对接缝传荷能力的影响。其中,h1,E1,μ1分别为面层的厚度、弹性模量、泊松比;h2,E2,μ2分别为基层的厚度、弹性模量、泊松比;k为地基反应模量;P为接地压力。面层板块间通过传力杆连接,接缝传荷由集料嵌锁和传力杆共同完成。传力杆和面层混凝土的结合状况由水平约束模量和竖向支撑模量表征。路面面层与基层的接触状况服从改进了的Walraven模型[12]。
|
| 图 1 计算模型Fig. 1 Calculation model |
为放大接缝处的传荷效应,设置矩形荷载分别作用于横缝中部和横缝边缘,如图 1(b)所示,荷载等效面积为20 cm×15 cm,接地压力分500,700 kPa 和900 kPa 3个级位进行。
1.3 计算参数选择
计算模拟的路面结构组合为水泥混凝土面层+贫混凝土基层。水泥混凝土面层参数:平面尺寸为500 cm×400 cm,厚度h1为26 cm,弹性模量E1为30 GPa,泊松比μ1为0.15,线膨胀系数α为10-5;贫混凝土基层参数:平面尺寸为500 cm×400 cm,厚度h2为20 cm,弹性模量E2为25 GPa,泊松比μ2为0.2;面层、基层分别按照100×80×5,100×80×4进行网格划分。传力杆模量E为200 GPa,泊松比μ为0.3;地基的反应模量k(E0,μ0)为30 MPa/m。
接缝处集料嵌锁剪切刚度取20 MPa/m,接缝张开量取0.5 mm;面层与基层间的剪切刚度取0.02 MPa/mm,剪力-位移曲线上拐点位移为4.1 mm。假定传力杆与混凝土结合状态理想,则混凝土对传力杆的水平约束模量取0 MPa,传力杆对混凝土的竖向支撑模量取1 200 MPa。根据公路自然区划,面层温度梯度取83 ℃/m。 2 弯沉传荷系数的计算与分析
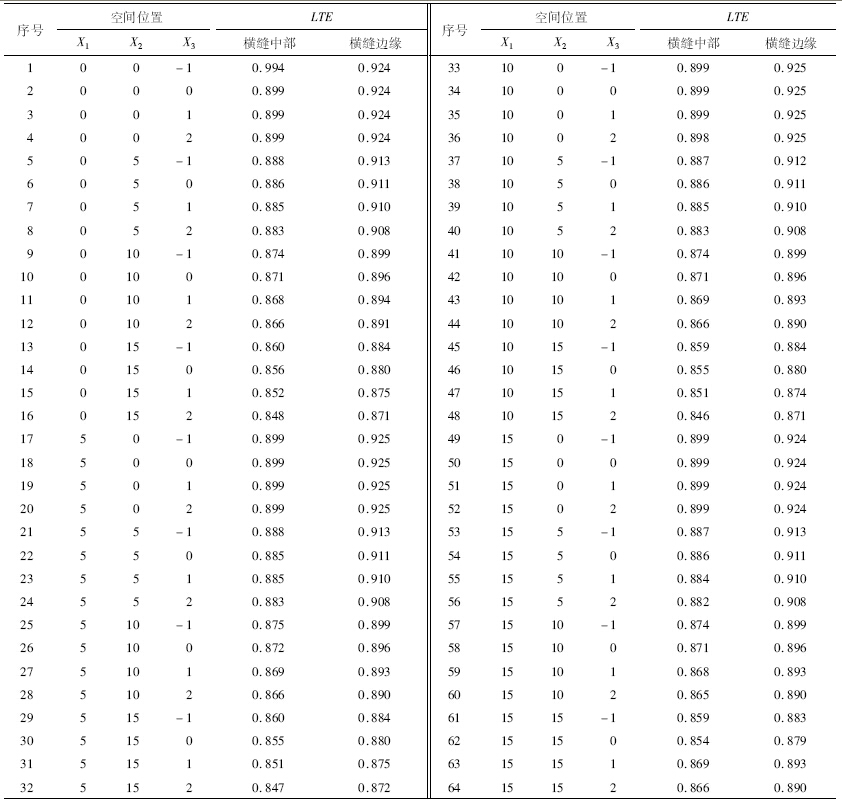
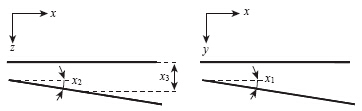
为明确传力杆水平偏角、竖直偏角和埋深偏差对弯沉传荷系数(LTE)、传力杆内力及板底应力的影响,采用单因素分析法,逐一计算3因素在各水平下的弯沉传荷系数。各因素的水平如表 1所示,其中,水平偏角、竖直偏角指传力杆均向左/右或上/下偏离,埋深偏差指传力杆中心在竖直方向上的位移,0为面层中部,-为中部靠上,+为中部靠下,具体偏差标记方法如图 2所示。
| 影响因素 | 基准 | 水平 | |||
| 水平偏角/(°) | 0 | 0 | 5 | 10 | 15 |
| 竖直偏角/(°) | 0 | 0 | 5 | 10 | 15 |
| 设置深度/cm | 0 | -1 | 0 | +1 | +2 |
|
| 图 2 传力杆位置偏差标记方法示意Fig. 2 Marking method of dowel bar position deviation |
在表 1所示的传力杆各种偏差水平下,相邻板块混凝土面层横缝中部、边缘弯沉计算结果如表 2所示。测试荷载大小一定时,荷载作用于横缝边缘的传荷能力较作用于横缝中部时大。无论荷位如何,传力杆水平偏角对弯沉传荷系数影响很小,竖直偏角则影响较大,随竖直偏角的增大,弯沉传荷系数线性减小,水平偏离15°时,传荷系数降低约12%。同时,传力杆布置于面层中部时,传荷系数最大,埋设位置偏上或偏下都将引起传荷系数的下降,偏下2 cm时降幅可达10%。
为准确预估传力杆位置偏差造成的传荷能力损失,利用Legendre正交多项式(式2),构造三维空间内的一般多项式函数(式3)。其中,i,j,k依据(1,2,3)的6种排列取值。首先,在置信度0.95的水平下,通过三元非线性回归得到6种排列下的f(x1,x2,x3)。然后,计算各自的复相关系数,并依据相关系数取最大值的原则确定i,j,k的取值。最终,确定唯一的f(x1,x2,x3)。

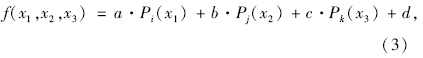
式中,a,b,c分别为x1,x2,x3项的回归系数;d为常数项。
荷载作用于横缝中部时,弯沉传荷系数的6种回归结果的复相关系数、F统计量如表 3所示。可知排列3(2,1,3)的回归结果适应性最好,因此,荷位在横缝中部时的接缝传荷能力可由模型一(式4)预估。同理,荷位在横缝边缘时弯沉传荷系数的6种回归结果的复相关系数、F统计量如表 4所示,其接缝传荷能力可由模型二(式5)预估。
| 排列号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 复相关系数(R) | 0.928 | 0.882 | 0.992 | 0.893 | 0.945 | 0.931 |
| P(F统计量) | 6.71e-13 | 2.53e-10 | 4.40e-16 | 2.41e-12 | 1.04e-15 | 2.28e-13 |

| 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 复相关系数(R) | 0.945 | 0.894 | 0.982 | 0.890 | 0.969 | 0.947 |
| P(F统计量) | 5.70e-29 | 6.65e-21 | 1.67e-43 | 1.66e-20 | 9.65e-43 | 1.580e-29 |
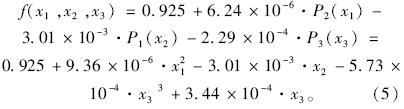
由于传荷能力预估模型f(x1,x2,x3)的荷载条件、传力杆抗弯刚度、传力杆与混凝土结合状况与实际路面结构均存在差异。因此,为提高预估模型的可靠性,需要从这3个角度通过FWD实测接缝两侧的弯沉[13],借助荷载修正系数η1、抗弯刚度修正系数η2、结合状况修正系数η3对模型进行修正,新的传荷能力预估模型LTE=f(x1,x2,x3,x4,x5,x6),如式6所示:
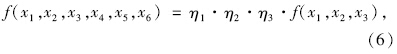
首先选择某一级公路,采用德国MIT SCAN2_BT路面拉杆传力杆测定仪测定传力杆实际空间位置(x1,x2,x3),再借助PRIMA-X 落锤弯沉仪量测横缝中部、边缘两个位置处的接缝传荷能力。
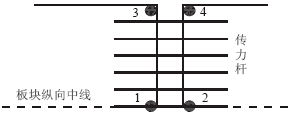
所测试路段路面结构为:28 cm水泥混凝土面层+20 cm水泥稳定碎石基层。板长约5.5 m,传力杆(长50 cm、直径32 mm、间距约30 cm)沿横缝均匀布置。道路已投入使用2 a,目前路面使用状况良好。测试时,首先将测得的传力杆深度、侧向滑移、水平滑移以及垂直错台换算为水平偏角、竖直偏角和竖直位移,然后采用拖车式落锤弯沉仪进行横缝中部、边缘两个位置的弯沉测试,测点布置如图 3所示,其中C1,C3分别为受荷板横缝中部、边缘测点,C2,C4分别为非受荷板横缝中部、边缘测点。
|
| 图 3 FWD测试点位布置Fig. 3 Arrangement of FWD measuring points |
为使弯沉实测环境更加贴近理论计算条件,选择在17:00(实测面层温度梯度为78 ℃/m)进行。同时,考虑到x5,x6的理论值与实测值差别较小[14],因此,η2,η3均取1,针对x4分3个测试水平(500,700 kPa和900 kPa)分别对f(x1,x2,x3)进行修正。经荷载修正系数η1线性平滑后,得到的弯沉传荷系数预估值f(x1,x2,x3,x4,x5,x6)和实测值(700 kPa接地压力下)如表 5所示,残差均小于0.022,相关系数到达0.976,较好地反映了真实弯沉传荷系数。
| 序号 | 空间位置 | LTE | |||||||
| X1/ (°) |
X2 (°) |
X3/ cm |
横缝中部 | 横缝边缘 | |||||
| 实测值 | f(x1,x2, x3,x4, x5,x6) |
残差 | 实测值 | f(x1,x2, x3,x4, x5,x6) |
残差 | ||||
| 1 | 4.6 | 11.5 | 0.8 | 0.843 | 0.860 | 0.017 | 0.931 | 0.938 | 0.007 |
| 2 | 4.0 | 5.9 | 1.3 | 0.897 | 0.889 | 0.008 | 0.956 | 0.955 | 0.001 |
| 3 | 6.8 | 9.5 | -0.2 | 0.725 | 0.728 | 0.003 | 0.938 | 0.944 | 0.006 |
| 4 | 3.5 | 6.2 | -1.5 | 0.917 | 0.910 | 0.007 | 0.951 | 0.956 | 0.005 |
| 5 | 0.3 | 0.0 | 0.4 | 0.961 | 0.976 | 0.015 | 0.968 | 0.974 | 0.006 |
| 6 | 7.3 | 10.8 | 1.1 | 0.676 | 0.690 | 0.014 | 0.943 | 0.940 | 0.003 |
| 7 | 1.5 | 0.0 | 0.4 | 0.973 | 0.965 | 0.008 | 0.962 | 0.974 | 0.012 |
| 8 | 3.7 | 3.8 | 1.7 | 0.904 | 0.899 | 0.005 | 0.929 | 0.934 | 0.005 |
| 9 | 0.0 | 0.0 | 0.2 | 0.970 | 0.976 | 0.006 | 0.978 | 0.974 | 0.004 |
| 10 | 7.4 | 11.2 | 1.5 | 0.697 | 0.686 | 0.011 | 0.958 | 0.962 | 0.004 |
| 11 | 6.4 | 7.8 | 0.8 | 0.741 | 0.758 | 0.017 | 0.984 | 0.962 | 0.022 |
| 12 | 3.3 | 1.8 | -0.2 | 0.924 | 0.918 | 0.006 | 0.973 | 0.972 | 0.001 |
对于3个级位的测试荷载,荷载修正系数η1的取值如表 6所示。
| 荷载/ kPa |
500 | 700 | 900 | |||
| 横缝中部 | 横缝边缘 | 横缝中部 | 横缝边缘 | 横缝中部 | 横缝边缘 | |
| η1 | 1.16 | 1.12 | 1.08 | 1.05 | 0.93 | 0.95 |
(1)针对刚性路面传力杆空间位置偏差问题,建立了Winkler地基上考虑层间接触状况的等平面尺寸双层路面结构模型。该模型可实现在考虑层间实际接触状态的前提下,考查传力杆位置偏差(水平偏角、竖直偏角和埋深偏差)对接缝传荷能力的影响。
(2)通过三元非线性回归构建了考虑传力杆位置偏差的接缝传荷能力预估模型,提出了模型的荷载修正系数η1并推荐了其取值范围。经FWD实测弯沉传荷系数的验证,修正后的预估模型较好地反映了传力杆位置偏差的刚性路面接缝传荷能力。
(3)传力杆水平偏角对弯沉传荷系数影响很小,随着竖直偏角的增大,弯沉传荷系数几乎线性下降,水平偏离15°时,传荷系数降低约12%。同时,传力杆布置于面层中部时,弯沉传荷系数最大,埋设位置偏上或偏下都将引起传荷系数的下降,偏下2 cm时降幅可达10%。
| [1] | ZOLLINGER D G, SOARES J. Performance of Continuously Reinforced Concrete Pavements (Volume VII): Summary, WA-RD-98-102[R]. Virginia: Federal Highway Administration, 1999. |
| [2] | IOANNIDES A M, ALEXANDER D R, HAMMONS M I, et al. Application of Artificial Neural Networks to Concrete Pavement Joint Evaluation[J]. Transportation Research Record, 1996, 1540: 54-64. |
| [3] | 陈飞,张宁,林亚萍,等.刚性路面传力杆接缝传荷能力评价新方法[J].交通运输工程学报,2006,6(4):47-51. CHEN Fei, ZHANG Ning, LIN Ya-ping, et al. New Load-transferred Evaluating Method at Doweled Joint of Rigid Pavement [J]. Journal of Traffic and Transportation Engineering,2006,6 (4):47-51. |
| [4] | 周正峰,凌建明,袁捷,等.机场刚性道面接缝传荷能力的评价[J].同济大学学报:自然科学版,2010,38(6): 844-849. ZHOU Zheng-feng, LING Jian-ming, YUAN Jie, et al. Evaluation of Load Transfer Efficiency at Joints for Rigid Airport Pavement[J]. Journal of Tongji University: Natural Science Edition, 2010,38(6): 844-849. |
| [5] | GUO Hua, SHERWOOD J A, SHYDER M B. Component Dowel-bar Model for Load-transfer System in PCC Pavements[J]. |
| [6] | 周德云,姚祖康.水泥混凝土路面接缝传荷能力的分析[J].同济大学学报:自然科学版,1993,21(3): 57-65. ZHOU De-yun, YAO Zu-kang. Analysis of Load Transfer at Joints in Concrete Pavements [J]. Journal of Tongji University: Natural Science Edition, 1993,21(3): 57-65. |
| [7] | 彭鹏,田波,牛开民.水平安装误差时传力杆工作性能研究[J].公路交通科技, 2011,28(6):62-66. PENG Peng, TIAN Bo, NIU Kai-min. Study on Working Performance of Dowel Bar with Horizontal Installation Errors[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6):62-66. |
| [8] | 申俊敏,李银榜. 重载旧水泥混凝土路面损坏调查与评价[J].山西交通科技,2012(1):15-17. SHEN Jun-min, LI Yin-bang. The Damage Survey and Evaluation of Old Cement Concrete Pavement under Heavy-load[J].Shanxi Science & Technology of Communi-cations, 2012(1):15-17. |
| [9] | 张艳聪,申俊敏,田波,等. 考虑层间接触的刚性路面传力杆设置的力学分析[J]. 公路交通科技,2013,30(4):22-27. ZHANG Yan-cong, SHEN Jun-min, TIAN Bo, et al. Mechanical Analysis of Dowel Bar Setting of Rigid Pavement Considering Interlayer Contact[J]. Journal of Highway and Transportation Research and Development, 2013, 30(4):22-27. |
| [10] | 程国勇,王帆,张献民,等. 荷载级位对接缝传荷能力影响规律的试验研究[J]. 中国民航大学学报,2011,29(4):49-51. CHENG Guo-yong, WANG Fan, ZHANG Xian-min, et al. Study on Correlation between Load Transfer Coefficient of Pavement Joint and Magnitude of Impact Load[J]. Journal of Civil Aviation University of China, 2011, 29(4):49-51. |
| [11] | DAVIDS W G, MAHONEY J P. Experimental Verification of Rigid Pavement Joint Load Transfer Modeling with EverFE [J]. |
| [12] | 周正峰.水泥混凝土路面接缝传荷能力的研究现状和发展趋势[J].公路,2011(7):49-52. ZHOU Zheng-feng. Current Status and Development Trend for Study on Load Transfer Efficiency at Joints for Cement Concrete Pavement[J].Highway,2011(7):49-52. |
| [13] | 唐伯明,邓学钧.刚性路面接缝传荷能力的评定与分析:FWD开发应用研究[J].东南大学学报,1991,21(6):84-89. TANG Bo-ming, DENG Xue-jun. Assessment of Load Transfer across Joints in Rigid Pavements using the FWD [J].Journal of Southeast University, 1991, 21(6):84-89. |
| [14] | 蒋应军, 戴经梁. 传力杆与混凝土界面的接触应力[J].中国公路学报, 2007, 20(2): 29-34. JIANG Ying-jun, DAI Jing-liang. Contact Stresses at Interfaces between Dowels and Surrounding Concrete [J]. China Journal of Highway and Transport, 2007, 20(2): 29-34. |
 2015, Vol. 31
2015, Vol. 31

 ,
,