公路交通科技  2015, Vol. 31 Issue (3): 46-50

扩展功能

文章信息

谈至明, 王力
TAN Zhi-ming, WANG Li
基于弯拉应力等效的地基当量回弹模量
Equivalent Resilient Modulus of Subgrade Based on Principle of Flexural-tensile Stress Equivalence
公路交通科技, 2015, Vol. 31 (3): 46-50
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 46-50
10.3969/j.issn.1002-0268.2015.03.008

文章历史

收稿日期：2014-05-30
引用本文 0
谈至明, 王力. 基于弯拉应力等效的地基当量回弹模量[J]. 公路交通科技, 2015, Vol. 31 (3): 46-50.
TAN Zhi-ming, WANG Li. Equivalent Resilient Modulus of Subgrade Based on Principle of Flexural-tensile Stress Equivalence[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 46-50.
基于弯拉应力等效的地基当量回弹模量
谈至明, 王力    
同济大学 道路与交通工程教育部重点实验室, 上海 201804
收稿日期:2014-05-30;
基金项目：国家自然科学基金项目(51378394).
作者简介: 谈至明(1960-),男,上海人,教授,博士生导师,工学博士.
通讯作者：谈至明(1960-),男,上海人,教授,博士生导师,工学博士.
摘要：以往多层地基的顶面当量回弹模量大多是按弯沉等效得出的,该值对计算地基上面层或基层的弯拉应力是不适合的.为此,在弯沉等效的地基顶面当量回弹模量计算式的基础上,通过对荷载圆半径的修正,将弯沉等效转变为弯拉应力等效;进而,总结出了三层结构时单圆和双圆荷载的荷载圆半径修正系数回归公式,并拓展至多层结构;最后,通过工程实例证实,用弯沉等效的地基顶面当量回弹模量计算刚性或半刚性基层层底弯拉应力偏小13%~22%,而用弯拉应力等效的地基顶面当量回弹模量计算得到的基层层底弯拉应力与理论值的误差不超过1%.
关键词： 道路工程     当量模量     弯拉应力等效     地基     弯沉等效    
Equivalent Resilient Modulus of Subgrade Based on Principle of Flexural-tensile Stress Equivalence
TAN Zhi-ming , WANG Li    
Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China
Abstract:In the past, the surface equivalent resilient modulus of multi-layer subgrade was obtained mostly based on the principle of deflection equivalence, which is not appropriate to calculate the flexural-tensile stress of surface or base course. For this reason, by modifying the load circle radius, the deflection equivalence is transformed into the flexural-tensile stress equivalence on the basis of the calculation method of the deflection equivalence surface equivalent resilient modulus of subgrade. Then, the regression formulas of the load circle radius correction coefficient of single circle and double circle of tri-layer structures are given, which is extended to multilayer structures. In the end, it is demonstrated by project examples that the bottom flexural-tensile stress under rigid or semi-rigid base calculated using the deflection equivalent subgrade surface equivalent resilient modulus is smaller and the deviation is about 13%~22%, while the deviation of the flexural-tensile stress calculated by the presented method is no more than 1%.
Key words: road engineering     equivalent modulus     flexural-tensile stress equivalence     subgrade     deflection equivalence    
0 引言

地基回弹模量是铺面结构设计的一个重要参数，其承载能力的强弱直接影响到路面结构的稳定性[1, 2, 3]。当土基经浅层处理或加铺粒料垫层时，地基当量回弹模量则是反映上述多层结构抵抗外荷载的综合刚度参数。如何综合多层结构抵抗荷载作用，国内外曾进行过大量研究：加拿大的Stolle等人研究了利用落锤式弯沉仪进行地基当量模量的估算方法[4]；美国的Vakili进行了路面结构层等效模量计算方法的探索[5]；法国的Asli等人与我国的刘汉清和段丹军等人利用便捷式挠度仪进行了地基顶面当量回弹模量换算方法的研究[6, 7, 8]；谈至明、姚祖康等人给出了单圆轮载和双圆轮载作用下不同层间接触条件(光滑、连续)的双层结构顶面当量模量回归显式,多层结构的近似换算式[9, 10]；王振辉、蔡良才等人对双层弹性结构基层顶面当量回弹模量的换算作进一步的分析，建立了换算公式[11]。以上研究成果都是以弯沉等效为原则得到的，该当量回弹模量对于计算面、基层层底弯拉应力是不当量的。蒋应军、戴经梁等人比较了不同等效原则对水泥混凝土路面下基层顶面当量回弹模量换算结果的影响,指出基于弯沉等效的当量回弹模量会使板底拉应力计算值明显偏小，从而导致设计结果不安全[12, 13]。因此，有必要对基于弯拉应力等效的地基顶面当量回弹模量进行深入系统的研究。

1 地基顶面当量回弹模量的概念

地基(泛指道路、公路、港口堆场和机场跑道等铺面的基础)顶面当量回弹模量即是按照某种物理量(弯沉、弯拉应力或弯拉应变)相等的原则，将多层结构等效为半无限空间体(图 1)时所得到的一个地基综合回弹模量值。

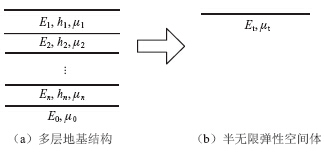
图 1 层状结构换算示意Fig. 1 Schematic diagram of layered structure conversion
图选项

基于弯沉等效的地基顶面当量回弹模量已进行过大量的研究：根据荷载中心点弯沉相等的原则，地基顶面当量回弹模量Et可表示为土基回弹模量E0与一系数ηl的乘积：

地基当量模量系数ηl为荷载半径δ、各结构层厚度hi、模量Ei和泊松比μi的函数，即：

基于弯沉等效原则换算得到的地基顶面当量回弹模量对计算面、基层层底弯拉应力(或弯拉应变)是不当量的，因此在计算面层或基层层底弯拉应力(或弯拉应变)时，应采用基于弯拉应力(或弯拉应变)等效的地基当量模量系数ησ(或ηε)。

在不计压应变影响的条件下，由于面层或基层层底弯拉应力与弯拉应变之间存在式(3)所示的关系[14]，因此，弯拉应力等效与弯拉应变等效实际上是等价的。本文仅讨论弯拉应力等效。 的函数，即：

式中，ε，σ，μ和E分别为面层或基层层底弯拉应变、弯拉应力、泊松比

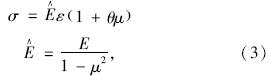
和弹性模量；Ê为面层或基层广义弹性模量；θ为与荷载形式和结构有关的系数，对于单圆荷载，θ=1，对于双圆荷载，θ一般在0.3~0.8之间。

为了处理方便及考虑到弯沉等效的地基顶面当量回弹模量在弯沉检测中的实用性，基于弯拉应力等效的地基项面当量模量系数ησ仍采用式(2)形式，通过对荷载圆半径的修正，使弯沉等效转变为弯拉应力等效。即基于弯拉应力等效的地基当量模量系数ησ计算式为：

式中kδ为荷载圆半径修正系数。

2 三层结构的荷载圆半径修正系数kδ

三层铺面结构示意图见图 2(a)。图中：面层模量Es=1 500~31 000 MPa、厚度hs=0.1~1 m、泊松比μs=0.15~0.3；第2层为土基经浅层处理层或加铺的粒料垫层，这里称为待换算层，模量Ex=80~600 MPa、厚度hx=0.2~0.5 m、泊松比μx=0.25~0.3；第3层为土基，模量E0=15~60 MPa、泊松比μ0=0.35，荷载半径δ=0.1~0.4 m。面层、换算层层间光滑，换算层、土基层间连续。

图 2 换算模型Fig. 2 Conversion model
图选项

利用弹性层状体系理论软件进行计算，得到三层铺面结构的面层层底最大弯拉应力为σ；同样方法得到，相同面层的双层铺面结构的面层层底最大弯拉应力为σ′；当σ′=σ时，即可得到换算层与土基的综合回弹模量Et；记相同换算层与土基条件下不同荷载圆半径时基于弯沉等效的地基顶面当量回弹模量为E′t,当E′t=Et时，即可得到荷载圆半径修正系数kδ。其换算模型如图 2所示。

计算结果表明：荷载圆半径修正系数kδ与面层的弯曲刚度半径ls和荷载圆半径δ之比ls/δ大致呈直线关系，如图 3所示。

图 3 kδ的回归关系Fig. 3 Regression relation of kδ
图选项

进一步研究发现：kδ随着δ,Ex,E0的增加而减小，随着Es的增加而增大，kδ的回归关系为：

式中，ls为面层相对于土基的刚度半径，ls=；λs,λx分别为面层、待换算层与土基的广义模量比，Ds，Dx分别为面层、待换算层的弯曲刚度，φ为与待换算层和面层的弯曲刚度比Dx/Ds有关的系数，散点如图 4所示，回归式见式(6)； α,β,γ和A,B,C为与荷载形式及结构有关的回归系数，见表 1。
图 4 φ的回归关系Fig. 4 Regression relation of φ
图选项
表 1 回归系数α，β，γ和A，B，C Tab. 1 Regression coefficients α，β，γ and A，B，C
荷载形式 α β γ A B C
单圆 0.03 -0.12 -0.10 -0.017 -0.136 0.492
双圆 0 -0.09 -0.16 -0.019 -0.155 0.654
表选项

将使用式(5)计算得到的kδ值代入式(4)求得基于弯拉应力等效的地基当量模量系数ησ，然后利用式(1)即可得到基于弯拉应力等效的地基顶面当量回弹模量Et。

在上述结构与材料参数范围内，地基顶面当量回弹模量Et回归计算残差的标准差为1.0 MPa(单圆)、0.8 MPa(双圆)，其相对误差均不超过4%，说明回归结果具有较好的精度。

3 多层结构时的换算

若地基有三层结构组成时，可按照弯曲刚度等效原则，先利用式(7)~式(10)计算得出一、二层的当量结构层的模量Ex、厚度hx、泊松比μx：

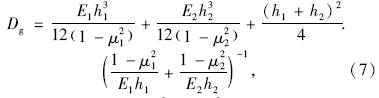
式中，Dg为平面变形时一、二层的总弯曲因度；E1,h1,μ1和E2,h2,μ2分别为不同粒料层的模量、厚度、泊松比。

然后利用三层结构的换算方法计算kδ，进而利用式(4)计算出修正系数ησ，最后根据式(1)求得地基顶面当量回弹模量 Et。在Ex=80~600 MPa范围内，按此方法计算的地基顶面当量回弹模量其相对误差最大不超过7%，由此回弹模量计算得到的面层层底弯拉应力，相对误差最大不超过1.5%，可以满足工程需要。

若地基结构超过三层，可采用式(7)~式(10)由上而下逐层换算：先利用式(7)~式(10)得到一、二层的当量结构层，进而得出一、二、三层的当量结构层，如此将地基换算成两层结构后，用式(1)、式(4)、式(5)和式(6)得到地基顶面当量模量。

铺面结构设置刚性或半刚性基层时，需将面层和基层合并为一层。当面层和基层层间连续时，面层和基层拥有同一弯曲中性轴，面、基层当量结构层的厚度hsb按式(11)计算，模量Esb可按式(12)计算:

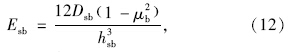
式中s，b分别为面层与基层。

Dsb按式(7)计算，只需将式中的Dg换成Dsb，下标1，2换成s，b。

面层和基层层间光滑时，面层和基层均无轴向力，但由竖向压应力和剪切应力引起的截面曲面变形将导致面层与基层弯曲曲率的不同，面层和基层的总的弯曲刚度Dsb按式(13)计算：

式中,Db为刚性或半刚性基层的弯曲刚度；ψ为面层与基层弯矩分配系数，按式(14)计算：

将式(11)计算得到的面层和基层的总的弯曲刚度Dsb代入式(8)和式(9)，只需将式中的Dg换成Dsb，Ex,hx换成Esb,hsb即可得到面、基层当量结构层的厚度hsb和模量Esb。最后将使用上述方法计算得到的Dsb,Esb,hsb代替式(5)和式(6)中的Ds,Es,hs即可荷载圆半径修正系数kδ。

在刚性、半刚性基层模量Eb=5 000~20 000 MPa范围内，按上述方法得到的地基顶面当量回弹模量的相对误差不超过5%(面、基层连续)、6%(面、基层光滑)，由此回弹模量计算得到的基层底面的弯拉应力的相对误差不超过1%，可以满足工程应用的需要。

若面层或半刚性基层由多层材料组成时，可直接使用式(7)~式(10)由上而下依次换算，直至将面层或基层合并成一层后，然后再使用上述方法求得kδ，最终将计算得到的kδ依次代入式(4)和式(1)即能得到基于弯拉应力等效的地基综合回弹模量Et。

4 应用实例

某沥青路面结构，其结构与材料参数如图 5所示。分别用弯沉等效与弯拉应力等效求单圆轮载(荷载圆半径0.15 m)和双圆轮载(荷载圆半径0.1 m)作用下得地基顶面当量回弹模量，并计算基层底面弯拉应力。

图 5 结构与材料参数Fig. 5 Structure and material parameters
图选项

计算步骤如下：

(1)首先由式(11)、式(12)计算面、基层当量结构层的厚度hsb与模量Esb。

(2)然后由式(7)~式(10)计算底基层与垫层的当量结构层的模量Ex、厚度hx、泊松比μx；这样，多层结构就被换算成了三层结构。

(3)最后计算地基顶面当量回弹模量。先由式(5)和式(6)计算荷载圆半径修正系数kδ，只需将式中下标s改为sb即可，然后根据弯沉等效的地基顶面当量回弹模量计算式(将ηl用ησ代替)得到基于弯拉应力等效的地基当量回弹模量(列于下表Et的第二行)，直接根据弯沉等效的地基顶面当量回弹模量计算式得到弯沉等效的地基顶面当量回弹模量(列于下表Et的第一行)。

(4)根据得到的地基当量回弹模量计算基层底面的弯拉应力σb1(弯沉等效)、σb2(弯拉应力等效)，与未经换算的直接应用弹性层状体系理论软件计算结果σb0进行比较，并计算其误差σbi-σb0σb0×100%(i=1,2)。

由表 2可以看出不能直接用弯沉等效计算得到的地基顶面当量回弹模量计算面层或刚性、半刚性基层底面的弯拉应力，这将使应力计算结果明显偏小，相对误差达到13%~22%。而应该用基于弯拉应力等效得到的地基顶面当量回弹模量进行计算，计算结果具有较高的精度，其误差不超过1%。

表 2 不同等效原则的应力计算结果比较 Tab. 2 Contrast of stresses calculated by different equivalent principles
荷载类型 Eb/MPa 6000 12000
Ex1/MPa 300 600 300 600
单圆
(δ=0.15 m)		 Et/MPa 弯沉等效 131.2 163.1 131.2 163.1
弯拉应力等效 50.4 53.8 48.2 50.8
σb/MPa σb0 0.366 0.362 0.468 0.465
σb1 0.317 0.305 0.407 0.394
σb2 0.366 0.363 0.468 0.465
误差/% 弯沉等效 -13.5 -15.82 -13.03 -15.36
弯拉应力等效 0.11 0.22 0.04 0.04
双圆
(δ=0.10 m)		 Et/MPa 弯沉等效 159.3 212 159.3 212
弯拉应力等效 46.2 49.4 44.1 47.3
σb/MPa σb0 0.312 0.308 0.399 0.396
σb1 0.254 0.24 0.328 0.312
σb2 0.31 0.307 0.397 0.393
误差/% 弯沉等效 -18.62 -22.21 -17.79 -21.24
弯拉应力等效 -0.42 -0.42 -0.43 -0.68
表选项
5 结论

(1)以往按弯沉等效得到的多层地基的顶面当量回弹模量对计算地基上面层或基层的弯拉应力是不适合的，因此提出了在弯沉等效的地基顶面当量回弹模量计算式的基础上，通过对荷载圆半径的修正，将弯沉等效转变为弯拉应力等效。

(2)荷载圆半径修正数kδ随着荷载半径δ、换算层模量Ex、土基模量E0的增加而减小，随着面层模量Es的增加而增大，总结给出了三层结构时的单圆和双圆荷载的荷载圆半径修正系数kδ的回归公式，并拓展至多层结构。

(3)通过工程实例证实，不能直接用弯沉等效计算得到的地基顶面当量回弹模量计算刚性或半刚性基层层底弯拉应力，这将使应力计算结果明显偏小，相对误差达13%~22%。而用本文方法得到的基层层底弯拉应力的误差不超过1%。

参考文献
[1] LING Jian-ming, QIU Xin, YUAN Jie. Determination of Subgrade Resilient Modulus for Existing Pavement Based on Moisture Condition Coupled with Stress [C]//Proceedings of the 2010 Geo Shanghai International Conference. Shanghai:[s.n.],2010:468-474.
[2] 官盛飞. 水泥混凝土路面路基工作状态与设计指标 [D]. 上海:同济大学,2009. GUAN Sheng-fei. Subgrade Work States and Design Index of Cement Concrete Pavement [D]. Shanghai: Tongji University, 2009.
[3] 谢国栋,贺梅,唐伯明. 基于FWD的路基材料反算模量修正系数研究 [J]. 中外公路, 2013,33(2):232-236. XIE Guo-dong, HE Mei, TANG Bo-ming. Study of Subgrade Materials Back Calculation Modulus Correction Coefficient Based on FWD [J]. Journal of China & Foreign Highway, 2013, 33(2):232-236.
[4] STOLLE D F E,JUNG F W. Estimate of Average Subgrade Moduli Using the FWD [C]//Proceedings of the 45th Canadian Geotechnical Conference, Toronto: Canadian Geotechnical Society, 1991:511-518.
[5] VAKILI J. A Simplified Method for Evaluation of Pavement Layers Moduli Using Surface Deflection Data [C]//The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics. Goa:[s.n.], 2008:4314-4319.
[6] ASLI C, FENG Z Q, PORCHER G, et al. Back-calculation of Elastic Modulus of Soil and Subgrade from Portable Falling Weight Deflectometer Measurements [J].
[7] 刘汉清, 黄伟, 杨岳,等. 应用PFWD检测新老路基路面回弹模量 [J]. 公路,2008(1):200-203. LIU Han-qing, HUANG Wei, YANG Yue, et al. Detection of New or Old Subgrade and Pavement Resilient Modulus Using PFWD [J]. Highway, 2008(1):200-203.
[8] 段丹军, 查旭东, 张起森. 应用便携式落锤弯沉仪测定路基回弹模量 [J]. 交通运输工程学报,2004,4(4):10-12. DUAN Dan-jun, ZHA Xu-dong, ZHANG Oi-sen. Subgrade Resilience Modulus Measuring by Portable Falling Weight Deflectometer (PFWD) [J]. Journal of Traffic and Transportation Engineering, 2004, 4(4):10-12.
[9] 谈至明, 姚祖康, 刘伯莹.层状结构顶面当量模量的近似计算[J].公路,2003,48(8):5-8. TAN Zhi-ming, YAO Zu-kang, LIU Bo-ying. A Approximate Calculation of Equivalent Modulus of End Face of Layered Structures[J]. Highway, 2003, 48(8):5-8.
[10] 姜爱锋, 姚祖康. 路面结构中地基顶面当量回弹模量的换算[J].同济大学学报:自然科学版,2001,29(5):536-540. JIANG Ai-feng, YAO Zu-kang. Calculation of Surface Equivalent Modulus of Subgrade in the Pavement Structure [J]. Journal of Tongji University:Natural Science Edition, 2001, 29(5): 536-540.
[11] 王振辉,蔡良才,顾强康,等. 基层顶面当量回弹模量确定方法的修正 [J]. 空军工程大学学报:自然科学版,2009, 10(6): 23-27. WANG Zhen-hui, CAI Liang-cai, GU Qiang-kang, et al. Modified Calculation Method of Equivalent Modulus of Elasticity of Foundation[J]. Journal of Air Force Engineering University: Natural Science Edition, 2009, 10(6): 23-27.
[12] 蒋应军, 戴经梁,陈忠达. 不同等效原则的基层顶面当量回弹模量算法 [J]. 长安大学学报:自然科学版,2005,25(3):1-6. JIANG Ying-jun, DAI Jing-liang, CHEN Zhong-da. Calculation Method of Equivalent Modulus of Elasticity of Foundation under Principles of Different Equivalence [J]. Journal of Chang'an University: Natural Science Edition, 2005,25(3): 1-6.
[13] 蒋应军, 侯传岭, 秦宪峰,等. 基层顶面当量回弹模量换算新方法 [J].公路交通科技, 2005,22(5):38-42. JIANG Ying-jun, HOU Chuan-ling, QIN Xian-feng, et al. Calculation Method of Composite Resilient Modulus of Foundation Under Cement Concrete Pavement [J]. Journal of Highway and Transportation Research and Development, 2005,22(5):38-42.
[14] 吁新华,谈至明. 沥青路面结构层弯拉应力与应变的近似计算 [J]. 同济大学学报:自然科学版,2012,40(6):849-853. YU Xin-hua, TAN Zhi-ming. Approximate Calculation of Flexural Stresses and Tensile Strains in Asphalt Pavements[J]. Journal of Tongji University:Natural Science Edition, 2012, 40(6):849-853.