公路交通科技  2015, Vol. 31 Issue (3): 37-45

扩展功能

文章信息

李怀健, 张鸿, 徐斌
LI Huai-jian, ZHANG Hong, XU Bing
准饱和土中单桩竖向荷载作用下的动力响应
Dynamic Responses of Single Pile Embedded in Nearly Saturated Soil Subjected to Vertical Load
公路交通科技, 2015, Vol. 31 (3): 37-45
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 37-45
10.3969/j.issn.1002-0268.2015.03.007

文章历史

收稿日期：2014-04-10
引用本文 0
李怀健, 张鸿, 徐斌. 准饱和土中单桩竖向荷载作用下的动力响应[J]. 公路交通科技, 2015, Vol. 31 (3): 37-45.
LI Huai-jian, ZHANG Hong, XU Bing. Dynamic Responses of Single Pile Embedded in Nearly Saturated Soil Subjected to Vertical Load[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 37-45.
准饱和土中单桩竖向荷载作用下的动力响应
李怀健1, 张鸿2, 徐斌2    
1. 交通运输部公路科学研究院, 北京 100088;
2. 南昌工程学院 土木与建筑工程学院, 江西 南昌 330099
收稿日期:2014-04-10;
基金项目：国家自然科学基金项目(51269021);江西省教育厅科技计划项目(GJJ13754).
作者简介: 李怀健(1973-),男,黑龙江虎林人,研究生,高级工程师.
通讯作者：李怀健(1973-),男,黑龙江虎林人,研究生,高级工程师.
摘要：根据Biot饱和多孔连续介质波动方程,基于Bardet对准饱和土的假设,提出了准饱和土二相介质波动方程;运用Helmholtz 矢量分解和传递、透射矩阵法(TRM)推导出准饱和土中层状半空间受竖向荷载作用下的动力响应表达式;利用Muki虚拟桩法,在层状半空间建立了桩和准饱和土相互作用的第二类Fredholm积分方程,通过离散的数值积分方法求解积分方程,讨论了准饱和土中单桩竖向动力响应问题.算例分析表明,准饱和土中桩顶竖向阻抗随饱和度的减少而增大,与饱和土地基相比,明显偏大;桩侧孔压随饱和度的减小而增大,并沿着桩长迅速衰减;桩顶位移幅值在频率较小时变化明显,饱和度越小,位移峰值越大,当频率较大时,饱和度的变化对振幅的影响不大.
关键词： 道路工程     准饱和土     单桩动力响应     Helmholtz 矢量分解     透射矩阵法(TRM)    
Dynamic Responses of Single Pile Embedded in Nearly Saturated Soil Subjected to Vertical Load
LI Huai-jian1 , ZHANG Hong2, XU Bing2     
1. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
2. School of Civil Engineering & Architecture, Nanchang Institute of Technology, Nanchang Jiangxi 330099, China
Abstract:A 2-phase medium wave equation of nearly saturated soil is proposed based on Biot's wave equation of saturated porous continuous media and Bardet's assumption regarding nearly saturated soil. Applying the Helmholtz's vector decomposition and transmission and TRM, the dynamic response expressions of layered half-space in nearly saturated soil under vertical load are derived. Based on Muki fictitious pile methodology, the second kind of Fredholm integral equations describing interaction between pile and nearly saturated soil in half-space are established. The integral equations are solved by using discrete numerical integral method, and the vertical dynamic response of a pile embedded in nearly saturated soil is discussed. The numerical result shows that (1) the vertical impedance at the top of the pile embedded in nearly saturated soil increases as the saturation degree decreases, and it is quite large compared with that of the saturated soil foundation; (2) the pore pressure along the side of the pile increases as the saturation degree decreasing, and attenuates rapidly along the length of the pile; (3) the pile top's displacement changes significantly when the frequency is small, a smaller saturation degree results in a larger peak displacement, but when the frequency is great, the changing of saturation degree does not have a major effect on the amplitude.
Key words: road engineering     nearly saturated soil     single pile dynamic response     Helmholtz vector decomposition     transmission and reflection matrix method (TRM)    
0 引言

桩土共同作用理论在机器基础、抗震结构设计中有着广泛应用，也是动力试桩的理论基础。1956年Biot首先建立了饱和两相介质动力固结方程，在工程中得到广泛应用，成为以后有关饱和多孔介质波动理论各项研究的基础[1, 2, 3, 4]。后来的一些学者致力于对Biot理论进行一些简化和修正，对土的动力研究有了很大的进展[5, 6, 7, 8, 9]。

然而，天然土体一般是固、液、气三相所组成的复杂材料体系，绝对意义上的干土或是饱和土是不存在的，工程上更为常见的是准饱和土，所以研究准饱和土与结构的动力响应具有比较重要的工程应用价值。而目前在准饱和土动力响应研究方面的文献不多见，Allen[10]等研究了准饱和砂中孔隙比和饱和度对压缩波传播速度的影响。Vardoulakis和Beskos[11]基于混合物理论推导了土-液-气三相动力场方程，并通过简化得到了实用的准饱和土三相介质波动方程。Bardet和Sayed[12]利用Biot理论和Vardoulakis和Beskos理论分别研究了在一维介质状况下压缩波传播速度和阻抗的衰减，并提出了一种压缩波在准饱和土传播中新的模型，Yang和Sato[13]利用Biot的两相介质理论对弹性波在准饱和土中的传播速度及其衰减进行了研究。以上文献都集中于波在准饱和土中传播特性的研究，而关于准饱和土中桩与土相互作用的动力响应研究则比较少。周洪峰[14]等基于Biot两相介质动力固结理论，考虑土体和流体的惯性及水土之间的耦合作用，研究了饱和度对地基上刚性基础竖向振动的影响。徐长节、马晓华[15]采用黏弹性两相介质模型，考虑土骨架的黏性以及流体与固体之间的耦合作用，采用数值方法分析了准饱和土中球形空腔的动力响应变化规律。

本文在前人研究的基础上，根据Biot饱和多孔连续介质波动方程，基于Bardet对准饱和土的假设，提出了准饱和土二相介质波动方程，运用Helmholtz 矢量分解和传递、透射矩阵法(TRM)法推导出了竖向荷载作用下准饱和土中层状半空间动力响应，利用Muki虚拟桩法，建立了桩和准饱和土相互作用的第二类Fredholm积分方程，通过离散的数值积分方法求解积分方程，研究了准饱和土层中桩的竖向振动特性。利用文中计算方法与已有结果比较，验证了此算法的正确性，通过算例分析得到了一些有益的结论。 1 基本理论及通解 1.1 控制方程

根据文献[16]，假设准饱和土中的气体以气泡形式存在于液体中，与液体共同形成各向同性的流体，气体与液体间的压力差忽略不计，这样把水与气等价为一种均质的流体，因此可使用两相孔隙介质理论来描述准饱和土。准饱和土中的孔隙水与气体组成的孔隙流体的体积模量Kf可近似表达为：

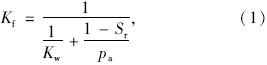
式中，Kf为流体的体积压缩模量；Kw为水的体积压缩模量；Sr为饱和度；pa为绝对流体压力。

则根据两相孔隙介质Biot理论[4, 17]，准饱和土体的本构方程可表示为：

式中，σij为土骨架应力；εij为土骨架应变张量；δij为克罗奈克符号；ui，Ui分别为土骨架和流体的位移；wi为流体的渗透位移(i,j=1,2,3)；pf为孔隙水压；λ，μ为土体的Lame常数；e和℘分别为土骨架体积应变和单位孔隙介质的流体体积增加量；n为孔隙率；α，M为与土体孔隙介质压缩有关的Biot参数。

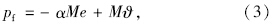
用位移ui，wi表示孔隙介质运动方程为：

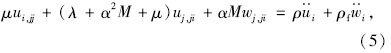
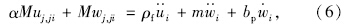
式中，ρ，ρf为孔隙介质密度和流体密度；ρs为土骨架的密度；m=a∞ρf/n，α∞为孔隙介质弯曲系数；bp=η/k，bp为土骨架与流体间的相互作用的耦合系数；η为孔隙介质黏性系数，k为孔隙介质的动力渗透系数。

参数α，M可用带有饱和度的参数水气流体体积模量Kf来表示：

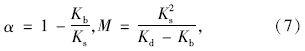
式中，Kd=KsKs,Kf为土颗粒和孔隙流体的体积模量；Kb为土骨架(干土状态)的体积模量。

1.2 控制方程通解

为了推导出频域内准饱和土控制方程的通解，这里定义如下Fourier变换：

式中，f(t)为时间域内函数；f(ω)为函数f(t)的Fourier变换。

对式(2)～式(6)按式(8)和式(9)进行Fourier变换，可得到频域内的控制方程。由于土体中存在两种P波(P1快波 和P2慢波)，ui可利用Helmholtz 矢量分解表示为：

式中，φf,φs为P1快波和P2慢波的标量势;ψk为剪切波的矢量势。根据文献[18]，孔压可以表示为：
式中Af,As由式(12)所确定：
式中，β1=mω2-ibpω；β2=α-ρfω2/β1；β3=ρω2-ρ2fω4/β1；β4=ρfω2-αβ1；β5=β1/M。

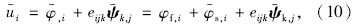
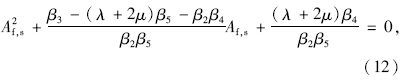
土骨架和流体的Helmholtz矢量势函数ψk可以退化成柱坐标下的两个标量势函数χ,η。利用方程式(2)～式(6)、式(11)和式(12)可推导出满足柱坐标下的Helmholtz 方程：

式中，kf，ks，kt为准饱和土中P1，P2和S波的复波数；ψ为剪切波的矢量势。kf，ks，kt可由式(16)确定：

半空间内部作用一任意力，其势函数、位移、孔压和应力可以展开成如下级数形式[20]：

将含有m 阶势函数的方程式(17)~式(27)代入Helmholtz 方程式(13)～式(15)，同时对柱坐标r进行Hankel变换[19]，求出频率-波数域基本解如下，具体推导过程可参见文献[20]。

2 第二类Fredholm积分方程的建立

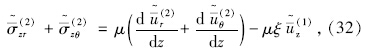
假设层状准饱和土体中埋入有一根桩，该桩的直径为d，桩长为L(d/L<<1)，其桩顶轴向作用有一简谐载荷Qeiωt，如图 1所示。根据Muki和Sternberg[21, 22]及Pak和Jennings[23]的方法，可以用两部分来表示问题的解：虚拟桩和扩展的层状准饱和土体，如图 2所示。准饱和土中单桩竖向荷载作用下的动力响应可由传递、透射矩阵法(TRM)来求解，这里限于篇幅，不再赘述，具体推导过程可参见文献[25]。另据文献[24]的报道，假设荷载是在低频范围内，通过计算分析，板透水与否对土体中板的竖向变形影响不明显，所以桩土之间接触界面的透水性在计算中可以不予考虑。

图 1 简谐荷载作用下层状准饱和土地基中单桩模型Fig. 1 Model of single pile embedded in layered nearly saturated soil foundation subjected to harmonic load
图选项

图 2 层状准饱和土中桩分解为扩展层状土体和虚拟桩Fig. 2 Pile embedded in layered nearly saturated soil decomposed into an extended layered soil and a fictitious pile
图选项

为了简化分析，本文以两层层状准饱和土体中的单桩响应进行分析，建立第二类Fredholm积分方程，对于其他多层土体情况可以采用相同的方法得到。土体模型分为两层，上层为一层土体，下层为半空间无限体。上层土体的Lame常量λ(1)，μ(1)，密度、厚度为ρ(1)，h；下层半空间无限体的Lame常量λ(2)，μ(2)，密度为ρ(2)。虚拟桩相应地分为2个部分。其杨氏模量、密度为[21, 22]：

式中，Ep，ρp分别为桩的杨氏模量和密度；Es(i)，ρ(i)(i=1，2)分别为层状土体的杨氏模量和密度，且Es(i)=μ(i)(3λ(i)+2μ(i))/(λ(i)+μ(i)) (i=1，2)。

记虚拟桩的轴力为N*(z)，桩侧竖向荷载为qz(z)。虚拟桩顶端和底部所受荷载分别为 N*(0),N*(L)，如图 2所示。层状半空间准饱和土所受荷载为：圆形区域Πz上的均布荷载为 qz(z)/A。桩顶和桩的底部所对应的圆形区域Π0和ΠL上的均布荷载分别为[P-N*(0) ]/A、N*(L)/A。其中A=πR2为桩的横截面积。

根据杆的振动理论，虚拟桩的轴力为 N*(z)，桩侧竖向荷载为qz(z)及桩身位移uzp*(z)有如下关系：

式中，uzp*(z)为虚拟桩的竖向位移；当0≤z≤h时，ρp*=ρ(1)p*，Ep*=E(1)p*；而当h≤z≤L时，ρp*=ρ(2)p*，Ep*=E(2)p*。

虚拟桩和层状土体接触面的协调条件为：沿桩轴向任意位置处虚拟桩的竖向应变与层状半空间准饱和土相同位置处的竖向应变应相等：

式中εzp*(z)为虚拟桩竖向应变。

沿桩轴方向扩展的层状半空间准饱和土竖向应变为：

式中ε(G)z(ζ,z)为竖向均布的圆形荷载作用在区域Πζ引起的圆形区域Πz的竖向应变，如图 2所示。

考虑到作用在虚拟桩上的轴力在两层的层间处不连续，因此，式(27)和式(29)中的积分应该在两层的层间处断开。

由式(26)～式(29)及式(25)可得：

式中，ε(G)z(z-,z)，ε(G)z(z+,z)为圆形区域Πζ作用均布竖向荷载从上部和下部无限趋近Πz处的竖向应变。

将式(36)，(37)和式(40)代入变形协调方程式(38)可得到层状准饱和土与桩体相互作用的Fredholm积分方程：

式中，Xa(ζ,z)=∫ζL[ρp*(η)ω2]εz(G)(η,z)dη； Xb(z)=∫0L[ρp*(η)Aω2]εz(G)(η,z)dη。

利用相同的方法，可得到Πz处扩展层状准饱和土体的竖向位移：

式中U(G)z(ζ,z)为在圆形区域Πζ处作用竖向均布荷载而引起Πz处的竖向位移。

式(41)中，桩顶的竖向位移uzp*(0)是未知的。可根据桩顶处位移与层状准饱和土表面处的位移相等而求得，即：

则uzp*(0)为：
式中，Xc(ζ,z)=∫Lζ[ρp*(η)ω2]u-z(G)(η,z)dη；

Xd(z)=∫L0[ρp*(η)Aω2]uz(G)(η,z)dη。

真实桩Πz位置处的轴力由两个部分叠加而成，虚拟桩的轴力和Πz处扩展层状处的竖向力：

式中，f(G)(ζ,z)大小为σz(G)(ζ,z)×A； σz(G)(ζ,z)为在圆形区域Πζ处作用一均布竖向荷载而引起的Πz处的竖向应力。

沿桩侧的孔压为：

式中p(G)f(ζ,z)为圆形区域Πζ的竖向均布荷载作用引起的Πz周边处的扩展层状准饱和土体的孔压。

3 数值验证与算例分析 3.1 数值验证

考察层状准饱和土体中有一截面为圆柱形的桩，其直径为d，桩长为L，杨氏模量和密度分别为Ep和ρp，有一轴向简谐荷载Qeiωt作用在桩顶上。在层状土体模型中，若每层土体的参数都相同，则层状土体与均质土体的解应该是相同的。层状土体这里取粉土进行计算分析，颗粒级配范围在 0.05 mm≤D≤0.075 mm，其他物理力学参数为：h(1)=h(2)=3.0 m，μ(j)=2.0×107 N/m2，λ(j)=4.0×107 N/m2，M(j)=2.44×108 N/m2，ρ(j)s=2.0×103 kg/m3，α(j)=0.97，n=0.4，b(j)p=1.94×108kg/(m3·s)，ρ(j)f=1.0×103 kg/m3，m(j)=1890 kg/m3，(j=1,2,3)。桩的参数为：d=1.0 m，L=10.0 m，Ep=5.3×108 N/m2，ρp=2.4×103 kg/m3，且参考长度aR=0.5 m。

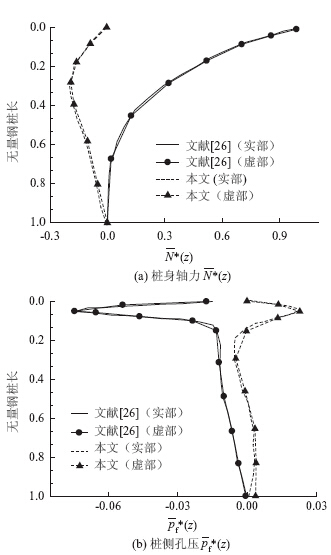
文献[26]给出了均质饱和土体中作用有轴向简谐荷载的桩的动力响应，利用本文的方法计算由层状土体退化为均质土体的解见图 3所示，文献[26]结果也列于图中。图中荷载频率ω无量纲化为ω*=轴力无量纲为N*(z)=N(z)/Q，桩侧孔压无量纲化为pf*(z)=πa2Rpf(z)/Q。从图中可以看出，当饱和度1-Sr=0时，本文的计算结果与文献[26]的结果比较吻合。

图 3 退化为均质土体后桩的动力响应结果与文献[26]比较Fig. 3 Comparison of presented results of dynamic response of pile embeded in homogeneous soil with those of Ref. [26]
图选项
3.2 算例分析

以两层准饱和土体中作用有轴向荷载的桩动力响应进行计算，分析不同饱和度情况下桩的竖向阻抗、轴力、桩侧孔压及桩顶位移的变化规律。饱和度考虑3种情况：①Sr=100%；②Sr=99%；③Sr=95%。每层的λ(j)=μ(j)，(j=1,2)。

(1)计算参数

两层的层状准饱和土体中埋入一单桩，其截面为圆形，桩顶轴向作用一简谐荷载Qeiωt。层状土体的第2层为半空间准饱和土体。这里取粉土进行分析，其颗粒范围在0.05 mm≤D≤0.075 mm，其他物理力学土体参数为：

桩的参数为：d=1.0 m，L/d=20，Ep/E(1)s=1000。

桩顶位移、荷载频率、孔压及桩身轴力无量纲化为：uzp**(0)=uzp*(0)aRμ(1)/Q、 ω*=ωaR pf*(z)=πa2R pf(z)/Q、 N*(z)=N-(z)/Q。定义层状土体中桩的竖向阻度kv=Q/[μ(1)aRup*(0)]，参考长度aR=0.5 m。

(2)饱和度对桩顶竖向阻抗kv的影响分析

准饱和土体中桩顶竖向阻抗kv与无量纲频率ω*= 0.0~0.5变化关系见图 4。从图 4中可知：在轴向荷载作用下，准饱和土中桩顶竖向阻抗kv的实部与虚部的绝对值随着土体饱和度的减少而增大，与饱和土体(饱和度为100%)相比，其竖向阻抗明显偏大，所以，土体中孔隙气体的存在使桩的动刚度增大，而其阻尼特性却在减弱。从图 4中可以看出，随着频率的增大，桩顶阻抗实部的绝对值越来越小，而其虚部在频率较小时，其绝对值随频率的增大而迅速增大，在频率较大时(无量纲频率ω*大于0.14)，其绝对值随着频率的增大反而减小，存在着明显的峰值。

图 4 不同饱和度下桩顶阻抗kv随荷载频率ω*的变化情况Fig. 4 Pile top impedance kv varying with load frequency ω* in different saturations
图选项

(3)饱和度对桩身轴力的影响分析

图 5表示荷载频率ω*=0.5时，桩身无量纲的轴力N*(z)沿桩长的变化情况。从图中可知：桩身无量纲的轴力N*(z)沿着桩深逐渐减少，轴力N*(z) 实部绝对值随着饱和度Sr的减小而逐渐增大，虚部绝对值在桩身上部分随着饱和度的减小而增大，而在桩的下部分则随着饱和度的增大而逐渐较小，存在一个明显的峰值。从总体上看，饱和度对桩的轴力有一定影响，但影响不大。

图 5 不同饱和度下桩身轴力N*(z)沿桩长的变化情况Fig. 5 Pile axial force N*(z) along length of

pile in different saturations

图选项

(4)饱和度对桩侧孔压的影响分析

图 6表示荷载频率ω*=0.5时，桩侧无量纲孔压pf*(z)=πa2Rpf(z)/Q沿桩长的变化情况。 从图中可知：均质土体中，桩侧无量纲孔压pf*(z)主要集中在桩的上端部位，pf*(z) 实部和虚部在桩端上部存在明显的变化，桩侧孔压随着饱和度的减小而增大，影响很大，并且沿着桩长迅速衰减；同时发现，对于层状土体，在层间处桩侧孔压有突变的现象。

图 6 不同饱和度下桩侧孔压pf*(z)沿桩长的变化情况Fig. 6 Pile side pore pressures pf*(z) along length of pile in different saturations
图选项

(5)饱和度对桩顶位移的影响分析

图 7表示荷载频率ω*=0.0~0.5时，桩顶无量纲位移uzp**(0)的变化情况。从图中可以看出，当桩的质量保持一定时，在ω*<0.2范围内，桩顶的位移幅值变化明显，土体的饱和度越大，其位移峰值反而越小，另外，准饱和土中桩顶位移最大幅值比饱和土的最大幅值大很多。在ω*>0.2，无量纲桩顶位移响应幅值变化不大，饱和度的变化对桩顶位移的影响也较小。

图 7 桩顶位移uzp**(0)与荷载频率ω*的变化关系Fig. 7 Displacement of pile top uzp**(0)varying with load frequency ω*
图选项
4 结论

根据Biot饱和多孔连续介质波动方程，基于Bardet对准饱和土的假设，提出了准饱和土两相介质波动方程。通过运用Helmholtz 矢量分解和传递、透射矩阵法(TRM)法推导出了简谐荷载作用下准饱和土中层状半空间基本解，利用Muki和Sternberg的虚拟桩法，建立了桩与半空间层状准饱和土相互作用的第二类Fredholm积分方程，求解出桩在轴向荷载作用下的动力响应。利用计算结果与已有结果相比较，二者相吻合，验证了算法的正确性。从本文的数值结果中可以得到如下结论：

(1)在轴向荷载作用下，准饱和土中桩顶竖向阻抗随着土体饱和度的减少而增大，与饱和土体(饱和度为100%)相比，其竖向阻抗明显偏大，所以，土体中孔隙气体的存在使桩的动刚度增大，而阻尼特性却在减弱。

(2)饱和度对桩身轴力有一定影响，但影响不大。

(3)桩侧孔压的变化主要集中在桩的上端部位，孔压随着饱和度的减小而增大，影响很大，并且沿着桩长迅速衰减，对于层状土体，在层间处桩侧孔压有突变的现象。

(4)在频率较小范围时桩顶位移值变化比较明显，饱和度越小，桩顶位移峰值就越大。准饱和土中桩顶的最大位移幅值比饱和土中的位移幅值大很多。频率较大时，饱和度的变化对振幅的影响不大。

参考文献
[1] BIOT M A. General Solutions of the Equations of Elasticity and Consolidation for a Porous Material[J]. Journal of Applied Mechanics,1956,27(1):91-96.
[2] BIOT M A. Theory of Deformation of a Porous Viscoelastic Anisotropic Solid[J].
[3] BIOT M A,WILLIS D G. The Elastic Coefficients of the Theory of Consolidation[J]. Journal of Applied Mechanics,1957,28(12):594-601.
[4] BIOT M A. Mechanics of Deformation and Acoustic Propagation in Porous Media[J].
[5] KASSIR M K,BANDYOPADHYAY K K, XU J. Vertical Vibration of a Circular Footing on a Saturated Half-space[J].
[6] KASSIR M K,XU J,BANDYOPADYAY K K. Rotatory and Horizontal Vibrations of a Circular Surface Footing on a Saturated Elastic Half-space[J]. International Journal of Solids Structures,1995,33(2):265-281.
[7] HALPERN M R,CHRISTIANO P. Steady-state Harmonic Response of a Rigid Plate Bearing on a Liquid-saturated Poroelastic Half-space[J].
[8] 刘林超,苏子平. 层状饱和土中单桩纵向振动分析[J].公路交通科技,2010,27(12):5-9. LIU Lin-chao,SU Zi-ping. Analysis of Vertical Vibration of Single Pile in Layered Saturated Soil[J]. Journal of Highway and Transportation Research and Development,2010,27(12):5-9.
[9] 张向东,刘家顺,张虎伟.循环荷载作用下软土动力特性试验研究[J]. 公路交通科技,2014,31(5):1-7. ZHANG Xiang-dong,LIU Jia-shun,ZHANG Hu-wei. Experimental Study on Dynamic Characteristic of Soft Soil under Cyclic Loading[J]. Journal of Highway and Transportation Research and Development,2014,31(5):1-7.
[10] ALLEN F A,RICHART F E, WOODS R D. Fluid Wave Propagation in Saturated and Nearly Saturated Sands[J]. Journal of Geotechnical and Geoenvironmental Engineering,1980,106(3):235-254.
[11] VARDOULAKIS I,BESKOS D E. Dynamic Behavior of Nearly Saturated Porous Media[J].
[12] BARDET J P,SAYED H. Velocity and Attenuation of Compressional Waves in Nearly Saturated Soils[J].
[13] YANG J, SATO T. On the Velocity and Damping of Elastic Waves in Nearly Saturated Soils[C]//Proceedings of the 33rd Japan National Conference on Geotechnieal Engineering. Osaka:Osaka University Press, 1998,1157-1158.
[14] 周洪峰,朱陆明,徐长节,等.准饱和土地基刚性基础的竖向振动分析[J].哈尔滨工业大学学报,2006,38(4):605-608. ZHOU Hong-feng,ZHU Lu-ming,XU Chang-jie,et al. Vertical Vibration of a Rigid Foundation on Nearly Saturated Soil[J]. Journal of Haerbing Institute of Technology,2006,38(4):605-608.
[15] 徐长节,马晓华.粘弹性准饱和土中球空腔的动力响应[J].岩土力学,2005,26(8):1189-1194. XU Chang-jie,MA Xiao-hua. Dynamic Response of Spherical Cavity in Nearly Saturated Viscoelastic Soils[J].Rock and Soil Mechanics,2005,26(8):1189-1194.
[16] VERRUIJT A. Elastic Storage of Aquifers[C]//Flow Through Porous Media. London:Academic Press,1969:331.
[17] BOIT M A. Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid,I,Low Frequency Range[J].
[18] BONNET G. Basic Singular Solutions for Poroelastic Medium in the Dynamic Range[J].
[19] MUKI R. Asymmetric Problem of the Theory of Elasticity for a Semi-infinite Solid and a Thick Plate[C]//Progress in Solid Mechanics 1960. New York:Interscience, 1960:399.
[20] LU J F,JENG D S,NIE W D. Dynamic Response of a Pile Embedded in a Porous Medium and Subjected to Plane SH Waves[J].
[21] MUKI R,STERNBERG E. On the Diffusion of an Axial Load from an Infinite Cylindrical Bar Embedded in an Elastic Medium[J].
[22] MUKI R,STERNBERG E. Elastostatic Load-transfer to a Half-space Form a Partially Embedded Axially Loaded Rod[J].
[23] PAK R Y S,JENNINGS P C. Elastodynamic Response of Pile under Transverse Excitations[J]. Journal of Engineering Mechanics,1987,113(7):1101-1116.
[24] HALPERN M R,CHRISTIANO P. Steady-state Harmonic Response of a Rigid Plate Bearing on a Liquid-saturated Poroelastic Half Space[J]. Earthquake Engineering and Structural Dynamics,1986,14(3):439-454.
[25] LU J F,HANYGA A. Fundamental Solution for a Layered Porous Half Space Subject to a Vertical Point Force or a Point Fluid Source[J].
[26] ZENG X,RAJAPAKSE R. Dynamic Axial Load Transfer from Elastic Bar to Poroelastic Medium[J]. Journal of Engineering Mechanics,1999,125(9):1048-1055.