扩展功能
文章信息
- 王芳, 刘凯, 王选仓, 金灿
- WANG Fang, LIU Kai, WANG Xuan-cang, JIN Can
- 旧水泥混凝土路面沥青加铺层结构可靠性分析
- Analysis of Structure Reliability of Asphalt Overlay on Old Cement Concrete Pavement
- 公路交通科技, 2015, Vol. 31 (3): 1-6,19
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (3): 1-6,19
- 10.3969/j.issn.1002-0268.2015.03.001
-
文章历史
- 收稿日期:2013-11-26
2. 重庆交通大学 交通土建工程材料国家地方联合工程实验室, 重庆 400074;
3. 合肥工业大学 交通运输工程学院, 安徽 合肥 230009;
4. 长安大学 公路学院, 陕西 西安 710064
2. National & Provincial Joint Laboratory for Transport, Civil Engineering and Material, Chongqing Jiaotong University, Chongqing 400074, China;
3. School of Transport Engineering, Hefei University of Technology, Hefei Anhui 230009, China;
4. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
路面可靠性指在计算使用期间保持路面整体使用特征(平整度、强度、粗糙度)的能力,可靠性水平的数学度量用可靠度表示。国内外研究学者利用数学模型[1, 2]、效应-抗力模型[3]或疲劳破坏概率模型[4],采用蒙特卡洛法[5, 6]、显式化法、响应面法[7]、一次二阶矩法[8]、直接积分[9]或有限元建模计算[10, 11, 12]等方法,通过可靠度基本理论计算分析[13]、检测和评价[13, 14]道路桥梁工程中存在的技术问题。公路水泥混凝土路面设计规范(JTG D40—2011)中引入了可靠度指标和系数,使路面结构设计和评价方法更加优化。公路沥青路面设计规范(JTG D50—2006)暂未引入可靠度理论,而旧水泥混凝土路面沥青加铺层设计也未考虑可靠度因素。本文将以可靠度理论和效应-抗力模型为基础,提出旧水泥混凝土路面沥青加铺层可靠度分析 方法。通过分析具有反射裂缝的旧水泥板沥青加铺层结构在两种最不利荷载情况下的受力,运用一次二阶矩中心点法计算结构抗力,采用蒙特卡洛有限元模拟计算荷载效应,得出多种设计模式下加铺层结构的可靠度水平,该研究结果将为沥青加铺层设计及其性能评价提供理论基础。
1 旧水泥混凝土路面沥青加铺层破坏模式
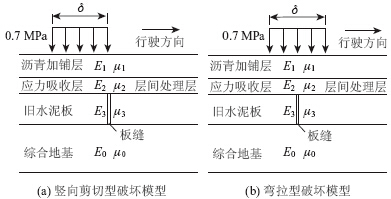
沥青加铺层的主要破坏形式有裂缝类破损和变形类破损,而基底旧水泥板本身的裂缝、横缝、纵缝在荷载作用下自下向上的反射裂缝是主要损坏类型之一。建立考虑反射裂缝的旧水泥板沥青加铺层结构,探讨不利荷位结构的可靠性。加铺层上轮载的动态运动(图 1)可看作先偏载受力,然后向前移动为对称荷载,故结构可靠性可认为由路表弯沉、层底弯拉应力和竖向剪应力这3个指标控制。图 1(a)为荷载作用于旧水泥板板缝上一侧(偏载),加铺层层底主要受竖直剪切破坏;图 1(b)为荷载对称作用于旧水泥板板缝上,沥青加铺层层底主要受弯拉破坏。图 2是偏载和对称荷载加载示意图。
|
| 图 1 加铺层破坏模式Fig. 1 Failure mode of asphalt overlay |

|
| 图 2 偏载和对称荷载示意图Fig. 2 Schematic diagram of eccentric load and symmetric load |
加铺层设计模式分为两类:一类为单层模式,即加铺罩面层改善路面状况;二类为层间处理和加铺沥青薄层,层间夹层有土工布、玻纤格栅、APP油毡、薄应力吸收层等。加铺层可单层或多层摊铺,分析中选取5种加铺模式:加铺1层沥青层、加铺1层沥青层和层间处理、加铺2层沥青层、加铺2层沥青层和层间处理、加铺3层沥青层。 2 旧水泥混凝土路面沥青加铺层可靠度分析方法 2.1 沥青加铺层可靠度基本理论
由可靠度的概念推测,沥青加铺层可靠度可定义为:沥青加铺层结构在实际环境、行车荷载作用下,在设计年限内,路表最大弯沉值不超过其设计弯沉、层底弯拉应力和剪切应力不超过其容许值的概率。若已知结构功能函数Z、荷载效应S和结构抗力R,则当Z=R-S>0时,表明结构处于可靠状态,能完成预定功能的概率称为可靠概率;当Z=R-S=0时,表明结构处于极限状态;当Z=R-S<0时,表明结构已失效,未能完成预定功能的概率称为失效概率。Z≥0事件的概率是结构可靠度,即Pr=P[Z=R-S≥0];失效概率Pf=P[Z=R-S<0],且Pr+Pf=1。可靠度指标β=(R-S)/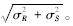 。R,σR和S,σS分别为结构抗力和荷载效应的平均值和标准差,则可靠度Pr=Φ(β)=1-Φ(-β)。 Φ(·)为正态分布函数。
。R,σR和S,σS分别为结构抗力和荷载效应的平均值和标准差,则可靠度Pr=Φ(β)=1-Φ(-β)。 Φ(·)为正态分布函数。
我国沥青路面设计规范[15]中给出路面结构控制指标为轮隙中心点路表设计弯沉ld和各层层底容许拉应力σR,而在城镇道路路面设计规范中还考虑沥青层容许剪应力τR,本文重点考虑反射裂缝对加铺层可靠性的影响,故选取路表弯沉、沥青层底拉应力和沥青层底竖向剪应力作为控制指标,从而提出沥青加铺层效应-抗力概率模型:
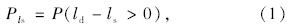

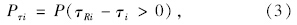
依据规范中设计弯沉、路面各层容许弯拉应力、剪应力表达式,运用一次二阶矩中心点法,即将抗力函数表达式在平均值处用Taylor级数展开,求解抗力的统计参数。其中:
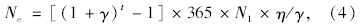



由式(5)得路表弯沉指标的均值、均方差和变异系数:
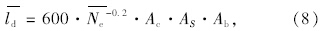
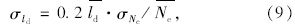

由式(6)得沥青层底弯拉应力指标的均值和变异系数:


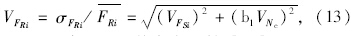
沥青层底竖向剪应力指标,以停车站、交叉口为例,由式(7)得其均值和变异系数:

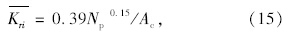
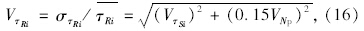
旧水泥板沥青加铺层采用复合路面弹性体系理论,以路表计算弯沉、每层层底弯拉应力和竖向剪切应力作为效应参数。运用ANSYS模型及其可靠性分析工具(Probabilistic Design-Monte-Carlo Simulations)计算效应的统计参数。
旧水泥板沥青加铺层ANSYS模型见图 1和图 3。路面结构层根据上述加铺模式设置,路基高度根据理论弯沉值大小进行调整,四周外延1 m;水泥板采用长5 m、宽4 m的两块板,横向水泥板缝宽为1 cm。分别施加对称荷载和偏荷载,见图 2;当量圆半径δ=10.65 cm,双圆荷载中心距为3δ,将其简化为18.9 cm×18.9 cm的正方形均布荷载,轮压为0.7 MPa。采用SOLID45单元,假设材料具有各向同性的线弹性特性,层间连续,边界条件为路面结构的左右两侧UX=0,前后侧面UY=0,基底面全部约束。路表弯沉计算点位位于双圆荷载轮隙中点A点;当计算层底(加铺层或层间处理层)最大拉应力或竖向剪应力时,经多次计算,点位取旧水泥板缝上方中心线与单圆荷载中心线(延行车方向)的交点B点或C点,因为该点的弯拉应力或竖向剪应力值均最大。

|
| 图 3 三维有限元模型Fig. 3 Three-dimensional finite element model |
根据设计的加铺层模式,参考相关文献和试验结果,确定各结构层材料的厚度、回弹模量、劈裂强度、剪切强度的均值和变异系数。通过有限元蒙特卡洛模拟计算,得到在对称荷载和偏荷载作用下的路表弯沉、各层层底拉应力、各层层底竖向剪应力的平均值、标准偏差和变异系数。 2.4 可靠度水平分析
加铺层可靠度用两种荷位弯沉可靠度的最小值、层底拉应力的可靠度和竖向剪切应力的可靠度来表征。根据β=(R-S)/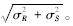 得到3个控制指标的可靠度指标:
得到3个控制指标的可靠度指标:

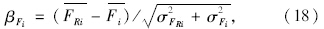
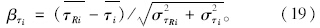
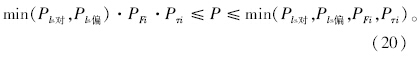
从研究成果的代表性和应用性考虑,以国道G104徐州机场路实际加铺结构为例,进行加铺层可靠度水平分析。对G104徐州机场路的交通量调查发现,从2004年到2006年(2005年、2006年双向日均标准轴载为9 207次/d和10 585次/d)交通量年增长率约为15%。据研究表明[10, 11, 12]:累计当量轴次Ne服从对数正态分布,其变异系数VNe约为0.30~0.40,对应2,4,6 a和8 a分别取0.3,0.35,0.4和0.4。G104为双向四车道,取交通量参数并代入式(4)计算,结果见表 1。
| η | γ | N1/ (次·d-1) |
Ne/(×104次) | |||
| 2 a | 4 a | 6 a | 8 a | |||
| 0.45 | 0.15 | 10 585 | 373.796 | 868.141 | 1 521.913 | 2 386.526 |
G104的实际加铺方案见表 2,以方案Ⅳ为计算示例,参考文献[15, 16]和试验结果选取计算参数,见表 3。运用上述荷载效应计算模型,建立有限元模型见图 3,模拟次数1 000次,计算荷载效应参数,结果见表 4和表 5。
| 加铺 方案 | Ⅰ 加铺1层 | Ⅱ 加铺1层+层间处理 | Ⅲ 加铺2层 | Ⅳ 加铺2层+层间处理 | Ⅴ 加铺3层 |
| 加铺结构 |
①5 cmAC- 16F+下封层 |
①5 cmAC-16F; ②2 cmSBS改性AC-5应力吸收层(层间处理层) |
①4 cmSBS改性AC-13C; ②5 cm AC-16F |
①4 cm SBS改性AC-13C; ②5 cm AC-16F; ③2 cm SBS改性AC-5应力吸收层(层间处理层) |
方案Ⅲ+③5 cm AC-20F |
| 板号 | 188~218 | 181~188 | 1~36 | 80~117 | |
| 里程 | K801+420~K801+555 | K801+388~K801+420 | K800+580~K800+740 | K800+940~K801+100 | |
| 长度/m | 135 | 32 | 160 | 160 |
| 加铺结构 | 厚度 | 抗压模量Ei/MPa | 15 ℃劈裂强度 | 25 ℃剪切强度 | μ | hi/cm | Vhi | 20 ℃ | 15 ℃ | VEi | FSi/MPa | VFSi | τSi/MPa | VτSi |
| ① SBS改性AC-13C | 4 | 0.1 | 1 500 | 2 000 | 0.10 | 1.2 | 0.10 | 2.0 | 0.10 | 0.25 |
| ② AC-16F | 5 | 0.1 | 1 200 | 1 800 | 0.15 | 1.2 | 0.10 | 1.8 | 0.10 | 0.25 |
| ③ SBS改性AC-5 | 2 | 0.1 | 600 | 1 000 | 0.15 | 1.0 | 0.15 | 1.5 | 0.15 | 0.3 |
| ④ 旧水泥板 | 22 | 0.05 | 28 000 | 28 000 | 0.12 | — | — | — | — | 0.15 |
| ⑤ 综合基础 | — | — | 300 | 300 | 0.25 | — | — | — | — | 0.35 |
| 注:hi,Ei,FSi,τSi为平均值;Vhi,VEi,VFSi,VτSi为变异系数;μ为泊松比 | ||||||||||
| 项目 | 路表弯沉/ (0.01 mm) |
①AC-13C 层底为压 应力,无拉 应力 |
②AC-16F 层底为压 应力,无拉 应力 |
③AC-5层底 拉应力/MPa |
||
| 平均值 | ls | 14.983 | F3 | 0.195 | ||
| 标准偏差 | σls | 2.832 | σF3 | 0.034 | ||
| 变异系数 | Vls | 0.189 | VF3 | 0.174 | ||
| 项目 |
路表弯沉/ (0.01 mm) |
层底竖向剪应力/MPa | ||||||
| ①AC-13C | ②AC-16F | ③AC-5 | ||||||
| 平均值 | ls | 13.889 | τ1 | 0.292 | τ2 | 0.253 | τ3 | 0.301 |
| 标准偏差 | σls | 2.472 | στ1 | 0.056 | στ2 | 0.047 | στ3 | 0.044 |
| 变异系数 | Vls | 0.178 | Vτ1 | 0.191 | Vτ2 | 0.187 | Vτ3 | 0.145 |
运用式(8)~式(16),以第6 a为例计算抗力参数。对称荷载时,以弯沉为指标,根据文献[15]选取Ac=1,As=1,Ab=1,将表 1中6 a的Ne=1 521.913×104次带入式(8),得到设计弯沉平均值ld=21.962(0.01 mm),由式(10)得变异系数Vld=0.2VNe=0.08,标准差σld=Vld·ld=1.757(0.01 mm)。以沥青层底拉应力为指标,AC-13C和AC-16F沥青加铺层均受压PF1=PF2=99.99%;SBS改性AC-5应力吸收层,将6 a的Ne带入式(12),其中根据文献[15]取a=0.09,b=0.22得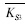 =3.423;由表 3知,
=3.423;由表 3知,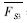 =1.0 MPa和VF3=0.15,代入式(11)得该层容许拉应力平均值
=1.0 MPa和VF3=0.15,代入式(11)得该层容许拉应力平均值 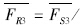 /
/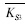 =0.292 MPa;式(13)得变异系数VFR3=
=0.292 MPa;式(13)得变异系数VFR3=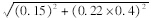 =0.174,标准差σFR3=
=0.174,标准差σFR3=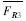 ·VFR3=0.292×0.174=0.051 MPa。同理可计算2,4 a 和8 a的抗力统计参数,见表 6。
·VFR3=0.292×0.174=0.051 MPa。同理可计算2,4 a 和8 a的抗力统计参数,见表 6。
| 参数 | 设计弯沉/(0.01 mm) | 参数 | ③AC-5层底弯拉应力/MPa | ||||||
| 2 a | 4 a | 6 a | 8 a | 2 a | 4 a | 6 a | 8 a | ||
| l d | 29.082 | 24.572 | 21.962 | 20.072 |
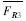
| 0.398 | 0.331 | 0.292 | 0.265 |
| Vld | 0.06 | 0.07 | 0.08 | 0.08 | VFR3 | 0.164 | 0.169 | 0.174 | 0.174 |
| Fld | 1.745 | 1.720 | 1.757 | 1.606 | σFR3 | 0.065 | 0.056 | 0.051 | 0.046 |
偏荷载时,设计弯沉统计参数见表 6。以竖向剪应力为指标,对于AC-13C层由式(15)得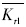 =3.943;由表 3知,
=3.943;由表 3知,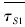 =2.0 MPa和VτS1=0.10,代入式(14) 得容许剪应力平均值
=2.0 MPa和VτS1=0.10,代入式(14) 得容许剪应力平均值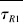 =0.507 MPa;由式(16)得变异系数VτR1=0.117,标准差στR1=0.059 MPa。同理,计算其他结构层及2,4 a和8 a的抗力统计参数,见表 7。
=0.507 MPa;由式(16)得变异系数VτR1=0.117,标准差στR1=0.059 MPa。同理,计算其他结构层及2,4 a和8 a的抗力统计参数,见表 7。
| 剪应力/MPa | ①4 cmAC-13C | ②5 cmAC-16F | ③2 cmAC-5 | |||||||||
| 2 a | 4 a | 6 a | 8 a | 2 a | 4 a | 6 a | 8 a | 2 a | 4 a | 6 a | 8 a | |
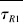
| 0.626 | 0.552 | 0.507 | 0.474 | 0.563 | 0.497 | 0.456 | 0.427 | 0.470 | 0.414 | 0.380 | 0.356 |
| VτR1 | 0.110 | 0.113 | 0.117 | 0.117 | 0.110 | 0.113 | 0.117 | 0.117 | 0.157 | 0.159 | 0.162 | 0.162 |
| στR1 | 0.069 | 0.062 | 0.059 | 0.055 | 0.062 | 0.056 | 0.053 | 0.050 | 0.074 | 0.066 | 0.061 | 0.057 |
由式(17)~(19),以第6 a为例计算可靠度指标。对称荷载时,结合表 4和表 6,由式(17)得βls对=
 =2.094,查正态分布表可知:Pls对=Φ(βls对
)=1-Φ(-βls对)=98.19%;式(18)得βF3=(0.292-0.195)/
=2.094,查正态分布表可知:Pls对=Φ(βls对
)=1-Φ(-βls对)=98.19%;式(18)得βF3=(0.292-0.195)/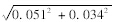 =1.583,查表得PF3=94.34%;由表 4知,方案Ⅳ的AC-13C和AC-16F层底都受压,认为其层底弯拉应力可靠度为PF1=PF2=99.99%。偏荷载时,结合表 5和表 7,式(17)得βls偏=2.662,查表得Pls偏=99.61%;式(19)得AC-13C,AC-16F,AC-5层底竖向剪应力的可靠度分别为Pτ1=99.59%,Pτ2=99.78%,Pτ3=85.31%。则6 a综合可靠度下限为98.19%×99.99%×99.99%×94.34%×99.59%×99.78%×85.31%=78.52%,可靠度范围为:78.52%≤P≤85.31%。同理,计算其他年限可靠度范围,见表 8。
=1.583,查表得PF3=94.34%;由表 4知,方案Ⅳ的AC-13C和AC-16F层底都受压,认为其层底弯拉应力可靠度为PF1=PF2=99.99%。偏荷载时,结合表 5和表 7,式(17)得βls偏=2.662,查表得Pls偏=99.61%;式(19)得AC-13C,AC-16F,AC-5层底竖向剪应力的可靠度分别为Pτ1=99.59%,Pτ2=99.78%,Pτ3=85.31%。则6 a综合可靠度下限为98.19%×99.99%×99.99%×94.34%×99.59%×99.78%×85.31%=78.52%,可靠度范围为:78.52%≤P≤85.31%。同理,计算其他年限可靠度范围,见表 8。
| 年限/a | Pls对 | PF1 | PF2 | PF3 | Pτ1 | Pτ2 | Pτ3 | P |
| 2 | 99.99 | 99.99 | 99.99 | 99.72 | 99.99 | 99.99 | 97.52 | 97.22≤P≤97.52 |
| 4 | 99.81 | 99.99 | 99.99 | 98.08 | 99.90 | 99.95 | 92.30 | 90.22≤P≤92.30 |
| 6 | 98.19 | 99.99 | 99.99 | 94.34 | 99.59 | 99.78 | 85.31 | 78.52≤P≤85.31 |
| 8 | 94.10 | 99.99 | 99.99 | 88.69 | 98.96 | 99.42 | 77.34 | 63.50≤P≤77.34 |
根据表 2的加铺方案,经有限元模拟和数值计算,得出加铺层结构的可靠度水平范围,见表 9。
| 加铺方案 | Ⅳ | Ⅴ | Ⅲ | Ⅳ | Ⅴ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 使用年限/a | 2~3 | 3~5 | 2~4 | 3~6 | 5~7 | 2~3 | 3~5 | 6~7 | 7~9 | 2~3 | 4 | 6 | 8 | 10 |
| 可靠度范围/% | 95~99 | 85~95 | 75~85 | 60~75 | ||||||||||
| 变异水平等级 | 低 | 低~中 | 中 | 中~高 | ||||||||||
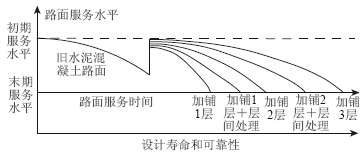
可见,为提高路面使用性能和使用寿命,应采用两层及两层以上的沥青混凝土层和层间处理的方案。该结果为选择在一定使用寿命和可靠度条件下的加铺层方案具有指导意义。图 4示意了两种加铺模式5种加铺方式的服务水平。
|
| 图 4 旧水泥混凝土路面沥青加铺层服务水平示意图Fig. 4 Schematic diagram of service level for asphalt overlay on old cement concrete pavement |
(1)在定性分析沥青加铺层弯拉和剪切破坏模式的基础上,以路表弯沉、沥青层底拉应力和层底竖向剪应力为指标,提出了旧水泥混凝土路面沥青加铺层可靠度分析方法。其中,根据可靠度理论建立沥青加铺层的效应-抗力概率模型,运用一次二阶矩中心点法构建抗力参数数学计算模型,将有限元模拟和蒙特卡洛法相结合建立两种破坏模式下效应参数计算模型,从而确定加铺层结构的可靠度水平。以G104徐州机场路实际加铺结构为例分析,给出了5种加铺层结构的可靠度范围。
(2)提出的加铺层可靠度分析方法提供了具有一定可靠度范围的结构设计值,若将该可靠度水平引入沥青加铺层结构设计中,将对改变现有依据经验推荐加铺方案的现状具有推动作用,且为沥青加铺层结构设计和评价提供理论参考。
| [1] | YOU K S,SUN L. Reliability Analysis of Vehicle Stability on Combined Horizontal and Vertical Alignments:Driving Safety Perspective [J]. |
| [2] | 刘小云,史春娟. 车辆荷载下沥青路面动力响应随机特性及可靠性分析[J]. 中国公路学报,2012,25(6):49-55. LIU Xiao-yun,SHI Chun-juan. Random Characteristics and Reliability Analysis of Asphalt Pavement Under Vehicle Random Load[J]. China Journal of Highway and Transport,2012,25(6):49-55. |
| [3] | 杨晨,程建川. 基于可靠度的道路不设缓和曲线最小半径的计算 [J]. 公路交通科技,2013,30(7):7-11. YANG Chen, CHENG Jian-chuan. Calculation of Minimum Circular Radius of Road without Transition Curve Based on Reliability [J]. Journal of Highway and Transportation Research and Development,2013,30(7):7-11. |
| [4] | ZHANG W,CAI C S,PAN F. Fatigue Reliability Assessment for Long-span Bridges under Combined Dynamic Loads from Winds and Vehicles [J]. Journal of Bridge Engineering,2012,18(8):735-747. |
| [5] | DILLIP D M,RAVI P,BABU G L S. System Reliability Analysis of Flexible Pavements [J]. |
| [6] | 苏永华,李伟. 锚网喷联合支护隧道稳定可靠度的拟蒙特卡洛分析 [J]. 公路交通科技,2012,29(1):109-113. SU Yong-hua,LI Wei. Analysis of Stability Reliability of Tunnel with Shotcrete Rockbolt Mesh Support via Quasi-Monte Carlo Method [J]. Journal of Highway and Transportation Research and Development,2012,29(1):109-113. |
| [7] | 李少宏,陈建军. 一种新的改进响应面法的结构可靠性计算方法 [J]. 中南大学学报:自然科学版,2013,44(5):1837-1841. LI Shao-hong,CHEN Jian-jun. A New Improved Response Surface Method for Structural Reliability Computing [J]. Journal of Central South University:Science and Technology Edition,2013,44(5):1837-1841. |
| [8] | 朱兴琳,方守恩. 公路路线设计可靠性分析 [J]. 公路交通科技,2009,26(10):135-138. ZHU Xing-lin,FANG Shou-en. Analysis on Reliability of Highway Alignment Design[J]. Journal of Highway and Transportation Research and Development,2009,26(10):135-138. |
| [9] | 李金平,焦生杰,陈建军,等. 结构可靠性分析的变量分解法 [J]. 西南交通大学学报,2014,49(1):79-85. LI Jin-ping,JIAO Sheng-jie,CHEN Jian-jun,et al. Dimension-reduction Method for Structural Reliability Analysis [J]. Journal of Southwest Jiaotong University,2014,49(1):79-85. |
| [10] | DESHPANDE V P,DAMNJANOVIC I D,DAMNJANOVIC I D et al. Effects of Overlay Designs on Reliability of Flexible Pavements [J]. |
| [11] | THYAGARAJAN S,MUHUNTHAN B,SIVANESWARAN N,et al. Efficient Simulation Techniques for Reliability Analysis of Flexible Pavements Using the Mechanistic-Empirical Pavement Design Guide [J]. |
| [12] | 徐旭,王祺国. 基于数值模拟的沥青路面结构可靠度分析 [J]. 公路交通科技,2008,25(5):18-22. XU Xu,WANG Qi-guo. Analysis of the Reliability of Asphalt Pavement Structure Based on Numerical Simulation[J]. Journal of Highway and Transportation Research and Development,2008,25(5):18-22. |
| [13] | 李志栋,黄晓明,陈广秀,等. 沥青混凝土路面可靠性水平评价研究 [J]. 北京工业大学学报,2012,38(8):1208-1213. LI Zhi-dong,HUANG Xiao-ming,CHEN Guang-xiu,et al. Research on Reliability Evaluation of Asphalt Pavement[J]. Journal of Beijing University of Technology,2012,38(8):1208-1213. |
| [14] | HAJEK J J,SELEZNEVA O,JIANG J Y,et al. Improving Reliability of Pavement Loading Estimates with Pavement Loading Guide [J]. |
| [15] | JTG D50—2006,公路沥青路面设计规范 [S]. JTG D50—2006,Specifications for Design of Highway Asphalt Pavement [S]. |
| [16] | CJJ 169—2011,城镇道路路面设计规范 [S]. CJJ 169—2011,Code for Pavement Design of Urban Road [S]. |
 2015, Vol. 31
2015, Vol. 31

 ,
,