扩展功能
文章信息
- 黄敏, 钮中铭, 李尔达, 张旭
- HUANG Min, NIU Zhong-ming, LI Er-da, ZHANG Xu
- 基于多目标优化的兴趣点指路标志布设模型
- Guide Sign Deployment Model of POI Based on Multi-objective Optimization
- 公路交通科技, 2015, Vol. 31 (2): 154-158
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 154-158
- 10.3969/j.issn.1002-0268.2015.02.024
-
文章历史
- 收稿日期:2014-06-09
设置科学合理的指路标志能使出行者方便快捷地到达目的地,从整体上提升交通系统的运行效率。因此,指路标志的布设备受关注。众多研究从不同的角度对指路标志的布设进行了探讨。为减少绕行和降低无效交通,有学者从驾驶人的出行心理出发,对路网节点进行等级划分,考虑交通吸引量、路网结构、土地利用等要素,提出了基于节点等级的分级指路系统的设计原则[1, 2, 3, 4, 5]。也有研究针对单个标志性地物(兴趣点),用圈层覆盖法来构建单目标的指路标志布设模型。模型以指引路径最短为目标,在一定范围内布设指路标志对兴趣点进行指引[6, 7]。在布设优化方面,有学者从均衡路网交通流等目标出发,合理选择指示路径,以此对指路标志的布设方案进行调整优化[8]。在实际工程应用中,常需要从某些给定的重要出入口开始到特定的兴趣点(如景点、大型公建等)规划一条指示路径,在上面设置指路标志对兴趣点进行指引,如广州亚运会城市道路交通设施升级期间,需要增设从快速路到亚运场馆的路径诱导标志。这条指引路径通常要满足多方面的因素,如从节省出行时间考虑,希望路径的长度足够短,路径上的交通流量尽量少;从实施管理成本来看,设置标志牌的数目要尽可能少等。
在这样的背景下,本文旨在构建一个搜寻从重要出入口到兴趣点最优指引路径的算法模型。其中最优指引路径综合考虑3个因素:指引路径的长度、交通量、布设指路标志的数量。为此,文中首先结合图论的理论对路网进行描述,然后定义用于衡量路径优化程度的综合指标,以网络分析为基础,结合广度优先搜索算法,对路网进行搜索,并动态更新优化指标,调整搜索范围,直至获得最优指引路径为止。最后,以广州大学城为例,对模型进行应用试验。实例表明,模型是有效、可行的。
1 多目标指引路径规划数学模型的构造 1.1 交通路网的表述
道路网络是指路标志布设的基础,本文以图论中的有向图对路网进行描述。以有向图G表示路网,G=(V,A),这里V={vi}为节点集,表示交叉口或分岔口;A={aij=
交叉口是交通路网的核心要素,在指路标志诱导系统建模中,常需要用到与交叉口相关的路网信息:交叉口物理连通关系,即交叉口与哪些弧段相邻;交叉口的几何特征,即弧段间的转向关系,如左转、右转等;交叉口的逻辑连通关系,相邻弧段间是否能直达,用于表述交叉口通行交通规则的弧段间的逻辑连通关系等。这些数据可以通过节点属性来记录,并应用于指路标志布设建模中,如弧段连通状态、交叉口几何特征等的推导,具体可参见文献[7, 9],本文不再展开。
1.2 指引路径的评价指标指引路径模型中考虑3个要素:指引路径长度、交通量、设置标志牌的数量,3者量纲不同。本文拟对优化目标进行归一化处理,并设定各指标重要程度一样。设从入口到兴趣点的最大参考距离为D,最大参考交通流量为Q,设置标志的最大数量N。若某指引路径的长度为dt,路径累计交通流量为dq,需设置的指路标志数量为n,则该路径的评价指标w的计算方法如式(1)所示。w值越小,说明路径越优。
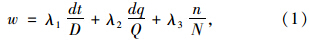
在指路标志的布设中,理想的状态是在指引路径的每个交叉口处都设置指向目的地的标志,但受限于标志牌面空间的约束,一般难以实现全路径设置。由前人的调研分析可知,在某些交叉口如果满足默认寻路规则,即使不设置指路标志也不会影响出行者寻路[11, 12, 13],如直行路口可省略。因此,在寻找最优指引路径过程中,可根据交叉口的状况判定是否需要设置指路标志。
下面建立寻找从入口到兴趣点最优指引路径的算法模型。算法的核心思想是从入口开始,以广度搜索算法为基础[14, 15],向外搜索路网,记录指引路径;在搜索过程中,计算指引路径的评价指标,并根据指标的取值动态调整记录路径,直至找到最优布设路径。算法模型中会用到以下符号:
list: 列表list用于存放算法中所有需考察的弧段a,a的属性结构为{flag,dt,len,dq,flow,pnt,set},具体含义如下。
a.flag:弧段搜索状态标识符,不同取值表达弧段处于何种搜索状态:a.flag=1,搜索路径已到达兴趣点,不需从a再向外搜索;a.flag=0,a处于当前搜索状态;a.flag=-1,a没被搜索过;a.flag=-2,路径到达a时已超过算法设定的上限,不需要搜索。
a.dt:从入口到弧段a当前路径的长度;
a.len:弧段a的长度;
a.dq:从入口到弧段a当前路径的累积交通累计流向;
a.flow:弧段a的交通流量;
a.pnt:在当前搜索路径中,弧段a的上一弧段;
a.set:在当前搜索路径中,到达弧段a为止需设置指路标志的数目;
schthd:搜索阈值,初始化取1;
enta:兴趣点的入口弧段,如果到达入口弧段,则此路径的搜索结束。
curvar:当前搜索路径的度量值,设当前搜索路径的最后一个弧段为a,由式(1)知curvar可由式(2)计算:
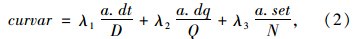
算法流程各步骤如下。
step1: 初始化,schthd=1;把重要入口所在的弧段a加入list中,其中,a.flag=-1,a.dt=a.len,a.dq=a.flew,a.pnt=-1,a.set=0。
step2: 从list取出一满足a.flag=-1的弧a,若不存在这样的弧,则转step9;否则转step3。
step3: 判断a是否为enta,若是,则a.flag=1,返回step2;若否,则转step4。
step4: 令a.flag=0,根据路网规则,找出与a逻辑连通的弧段a′,以距离兴趣点从近到远的顺序,对每个a′,以式(2)计算a′ 通过a到达重要出入口的路径度量值a′.curvar,按step5~step8更新弧段搜索状态标识符a′.flag,完成后返回step2。
step5: 若a′ 不在list中,若curvar
step6:若a′在list中,且a′.flag=-1,说明之前已有另一弧段搜索到a′;比较通过a的路径度量值a′.curvar′与原来路径的度量值curvar,如果curvar′
step7:若a′在list中,且a′.flag=0,说明a′之前已被搜索过,比较通过a的路径度量值curvar′与原来路径的度量值curvar,如果curvar′
step8:若a′在list中,且a′.flag=1,说明之前已从一条路径到达兴趣点,同step6处理,判断是否要更新路径。
step9:若a′在list中,且a′.flag=-2,则不用对a′进行处理,返回step4。
step10:算法结束。
在算法中,路径更新分为路段更新和路径局部更新。路段更新只需更新a′数据,a′.dt=a.dt+a′.len,a′.dq=a.dq+a′.flow,a′.pnt=a,a′.set可以根据设置规则来确定。如根据调研,在指路标志缺失时,出行者通常会选择直行路段[11]。在搜索路径上,前后连接的弧段是否直行可以根据路网的几何特征计算得[7, 9],这里不再展开。路径局部更新指需要在原来路径上从当前搜索路段a′开始更新直到通向兴趣点的最后一个路段。如图 1所示,设当前考查路段a=a94,当前搜索相邻路段a′=a45,a′之前被搜索到的上一路段a′.pnt=a34,路径2上的a45的度量值为curvar′,路径1上的a45的度量值为curvar。若curvar′ 寻找从入口到兴趣点最优指引路径的算法流程图如图 2所示,其中对当前弧段a的逻辑连通弧段a′ 进行处理的算法流程如图 3所示。搜索过程完成后,从兴趣点入口弧段开始,根据弧段的pnt属性,往前逆推重要入口,可得出整条指引路径。
以广州大学城为试验区域,利用上述模型计算出从南沙港快线到中山大学的最优指路标志布设路径,算法中使用直行路段作为优化方向。结合之前对指路标志数据可视化的研究工作[16],所得结果如图 4(a)所示;4(b)为有指路标志诱导路径的布设现状。 由1.2节可算得本试验所用式(1)的3个参数D,Q,N的值,见表 1。已知大学城中环路和外环路均为双向六车道,且机动车与非机动车间设有隔离带,假设路段均为车道宽为3.5 m,交叉口的绿信比为0.48,路段长度为300 m,由以上参数,利用文献[10]给出的方法算出路段通行能力C。表 2对应图 4中两种路径的3因素权重以及综合度量值。本试验认为路径长度、流量和设置标志牌数对路径选择的贡献值相同,因此取λ1=1/3,λ2=1/3,λ3=1/3。
由表 2可知,虽然路径a长度略大于路径b,但是路径a仅需要设置3个指路标志牌,而路径b需要设置5个。文献[17]给出的2020年设计中环路断面交通流量为23 000 pcu/d,外环为13 500 pcu/d,可算出路径a,b的累积交通流量,如表 2所示。由此3个指标算得两路径度量值分别为0.242 3和0.267 0。可见路径a更符合本文的多目标优化目标。
本文对兴趣点的指路标志布设进行了探讨,构建了一个为兴趣点规划综合考虑路径长度、标志设置数量和路径交通量的最优指引路径的算法模型。模型为工程布设提供了有效的理论依据。实际布设中还可以考虑更多的优化指标,如路段交通吸引量等。这些将在后续的研究中进行探讨。
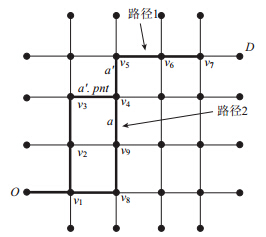
图 1 指引路径局部更新示意图Fig. 1 Partial update of guide path
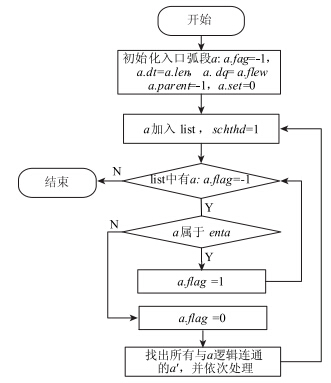
图 2 寻找最优指引路径算法流程图Fig. 2 Flowchart of algorithm for finding out optimum guide path
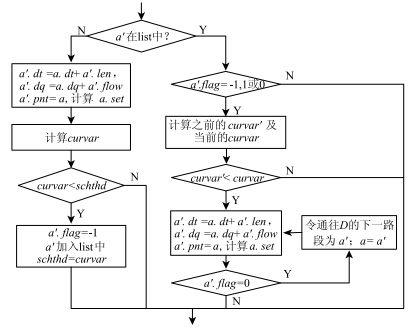
图 3 对一条弧段a′进行处理的算法流程图Fig. 3 Flowchart of algorithm for processing arc a′
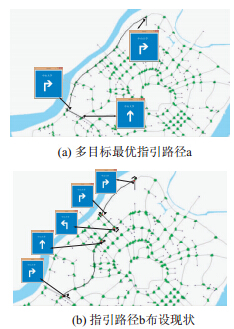
图 4 多目标优化指引路径与布设现状对比Fig. 4 Comparison of guide path created by multi-object optimization and current one
D/m
C/(pcu·d-1)
Q/(pcu·d-1)
N/个
6 957
302 400
4 965 156
46 路径
dt/m
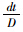
路段数
dq/(pcu·d-1)
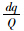
set/个
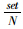
度量值
a
4 396
0.631 9
11
148 500
0.029 9
3
0.065 2
0.242 3
b
4 346
0.6247
15
335 500
0.067 6
5
0.108 7
0.267 0
| [1] | 王建军, 陈梦月, 常振文,等. 基于驾驶人出行心理的道路网指路系统设计[J]. 长安大学学报:自然科学版, 2009, 29(2): 75-79. WANG Jian-jun, CHEN Meng-yue, CHANG Zhen-wen, et al. Design of Guidance System of Road Network Based on Driver Trip Psychology[J]. Journal of Chang'an University: Natural Science Edition, 2009, 29(2): 75-79. |
| [2] | 邓兴栋. 城市道路指路标志信息选取方法研究[J]. 交通科学与工程,2010, 26(1): 97-102. DENG Xing-dong. Research on Selection Method of the Urban Road Directional Sign Information[J]. Journal of Transport Science and Engineering, 2010, 26(1): 97-102. |
| [3] | 蒋贵川, 易术. 城市环线高速公路指路标志系统优化设计研究[J]. 公路, 2009 (10): 147-152. JIANG Gui-chuan, YI Su. Research on Optimization Design of Guide Sign System for Urban Ring Expressway[J]. Highway, 2009(10): 147-152. |
| [4] | 李伟, 姜明, 唐琤琤. 公路指路标志系统的改进研究[J]. 公路交通科技, 2008, 24(12): 117-122. LI Wei, JIANG Ming, TANG Cheng-cheng. Study on the Improvement of Highway Guide Sign System [J]. Journal of Highway and Transportation Research and Development, 2007, 24(12): 117-122. |
| [5] | 郭敏,楼晓寅. 标志指路体系的模型[J]. 公路交通科技,2009, 26(10): 130-134. GUO Min, LOU Xiao-yin. Model of Travel Guide Sign System [J]. Journal of Highway and Transportation Research and Development, 2009, 26(10): 130-134. |
| [6] | 唐良. 城市道路交通指路标志智能设计系统的研究与实现[D]. 合肥:中国科学技术大学, 2008. TANG Liang. Research and Realization of an Intelligent Design System for Traffic Guide Signs in Urban Road Network[D]. Hefei: University of Science and Technology of China, 2008. |
| [7] | 黄敏, 余志, 肖国荣. 基于交叉口函数的城镇指路标志设置模型[J]. 交通运输工程学报, 2006, 6(4): 96-100. HUANG Min,YU Zhi, XIAO Guo-rong. Deploying Model of City Guide Signs Based on Intersection Functions[J]. Journal of Traffic and Transportation Engineering, 2006, 6(4): 96-100. |
| [8] | TOI S, KIYOTA M T, YOSHITAKE T, et al. A Method for Planning of Road Sign System in Highway Using Straying Index[J]. Journal of the Eastern Asia Society for Transportation Studies, 2005, 6: 981-996. |
| [9] | 黄敏, 余志, 张小兰. 基于交叉口特征的指路标志建模方法[J]. 西南交通大学学报, 2007, 42 (1): 110-114. HUANG Min, YU Zhi, ZHANG Xiao-lan. Modeling Method for Road Guide Signs Based on Intersection Features[J]. Journal of Southwest Jiaotong University, 2007, 42 (1): 110-114. |
| [10] | 王炜, 过秀成. 交通工程学[M]. 南京:东南大学出版社, 2000:152-156. WANG Wei, GUO Xiu-cheng. Traffic Engineering[M]. Nanjing: Southeast University Press, 2000:152-156. |
| [11] | 黄敏, 饶明雷, 李敏. 指路标志诱导系统指引连贯性分析及评价研究[J].公路交通科技, 2012, 29(11): 110-114. HUANG Min,RAO Ming-lei,LI Min. Analysis and Evaluation of Guiding Consistency in Guide Sign System[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 110-114. |
| [12] | UCHIDA T, IIDA Y, NAKAHARA M. Panel Survey on Drivers' Route Choice Behavior under Travel Time Information[C]//Proceedings of 5th International IEEE Conference on Vehicle Navigation and Information Systems Conference. Yokohama: IEEE, 1994: 383-388. |
| [13] | TAWFIK A M, RAKHA H A, MILLER S D. An Experimental Exploration of Route Choice: Identifying Drivers Choices and Choice Patterns, and Capturing Network Evolution[C]//Proceedings of 13th International IEEE Conference on Intelligent Transportation Systems. Madeira Island: IEEE, 2010: 1005-1012. |
| [14] | FRANCIOSA P G, FRIGIONI D, GIACCIO R. Semi-dynamic Breadth: First Search in Digraphs[J]. Theoretical Computer Science, 2001, 250(1/2): 201-217. |
| [15] | ZHOU R, HANSEN E A. Breadth: First Heuristic Search[J]. Artificial Intelligence, 2006, 170(4/5): 385-408. |
| [16] | 黄敏, 熊志, 赵梦扬. 基于路网拓扑结构的指路标志标识系统数据模型的研究与应用[J]. 测绘科学, 2008, 33(6): 21-22. HUANG Min, XIONG Zhi, ZHAO Meng-yang. Research and Application on Data Model of Road Guide Sign System Based on Road Network Topology [J]. Science of Surveying and Mapping, 2008, 33(6): 21-22. |
| [17] | 安云. 广州大学城智能交通管理系统及实施的研究[J]. 广东公安科技, 2004 (3): 60-63. AN Yun. Research of Intelligent Transport Management System and Its Implement in Guangzhou Higher Education Mega Center [J]. Guangdong Gongan Keji, 2004(3):60-63. |
 2015, Vol. 31
2015, Vol. 31
