扩展功能
文章信息
- 林梦凯, 冀伟, 李海莲
- LIN Meng-kai, JI Wei, LI Hai-lian
- 纯弯作用下波形钢腹板Ⅰ型钢梁的弹性弯扭屈曲分析
- Analysis of Flexural-torsional Buckling of Ⅰ-girder with Corrugated Steel Webs under Uniform Bending
- 公路交通科技, 2015, Vol. 31 (2): 89-93
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 89-93
- 10.3969/j.issn.1002-0268.2015.02.014
-
文章历史
- 收稿日期:2014-03-19
波形钢腹板I型钢梁是由上、下翼板和波形钢腹板焊接而成,其构造图如图 1所示。目前,国外学者对其剪切屈服强度和弹性弯扭屈曲荷载等力学特性进行过研究[1, 2, 3, 4, 5],其中文献[5]在假设剪力流在波形钢腹板上均匀分布的基础上,求得了波形钢腹板I型钢梁扭转中心的近似位置。但是国内对其研究较少,而且研究的主要目标集中在波形钢腹板预应力混凝土组合箱梁方面[6, 7, 8, 9, 10]。
本文以开口截面薄壁杆件的约束扭转理论为基础,推导出波形钢腹板I型钢梁约束扭转时扭转中心的精确位置,并求得以扭转中心为极点的主扇性惯性矩,在此基础上求得波形钢腹板I型钢梁的弹性弯扭屈曲临界荷载的计算公式。使用所得的计算公式对5片波形钢腹板I型钢梁进行弹性弯扭屈曲临界荷载计算,计算结果与ANSYS有限元结果吻合良好,验证了本文公式的正确性,同时分析了波形钢腹板I型钢梁波形的形状对弹性弯扭屈曲临界荷载的影响。

|
| 图 1 波形钢腹板I型钢梁的构造图 Fig. 1 Structure of I-girder with corrugated webs |
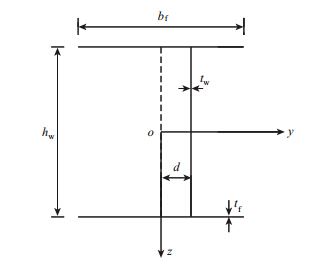
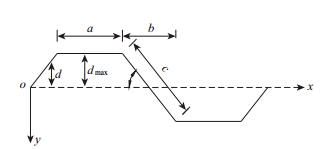
定义波形钢腹板I型钢梁上翼板与下翼板中心的连线构成的平面称为中面,如图 1所示。图 2所示为波形钢腹板I型钢梁的截面图,上、下翼板关于oy轴上下对称,上、下翼板关于oz轴左右对称,hw为波形钢腹板的高度;bf为上、下翼板的宽度;tf为上、下翼板的厚度;tw为波形钢腹板的厚度。图 3为波形钢腹板的波形示意图,θ为波形钢腹板的波折角度;d为波形钢腹板的波高,波高沿梁纵向(ox轴方向)是变化的,变化范围为0≤d≤dmax;a为波形钢腹板的平板长度;c为波形钢腹板的斜板长度;b为波形钢腹板的斜板在ox轴上的投影长度。
|
| 图 2 波形钢腹板I型钢梁的截面图 Fig. 2 Cross-section of I-girder with corrugated webs |
|
| 图 3 波形示意图 Fig. 3 Corrugation profile |
为了求得扭转中心在波形钢腹板I型钢梁横截面的确切位置,需要做一参考扇性面积图,设参考极点选在B点(腹板与上翼板的交点),并以此为零点,做参考扇性面积图,记做ωB图,见图 4,同时做出波形钢腹板I型钢梁截面的z图,见图 5。

|
| 图 4 参考扇性面积ωB图 Fig. 4 Reference sectorial area ωB |

|
| 图 5 波形钢腹板I型钢梁的截面z图 Fig. 5 z coordinates of I-girder with corrugated webs |
由文献[11]可知,如果认为C点为所求的扭转中心,B点为参考极点,则扭转中心的计算公式,见式(1)与式(2),
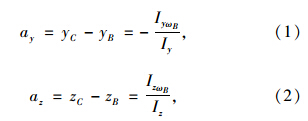
式中,ay为扭转中心与参考极点y坐标之差;az为扭转中心与参考极点z坐标之差;IzωB=∫AωBydA为参考极点的扇性坐标与直角y坐标的惯性积;IyωB=∫AωBzdA为参考极点的扇性坐标与直角z坐标的惯性积;Iz=∫Ay2dA与Iy=∫Az2dA分别为截面对y和z的惯性矩。
对于图 2所示的波形钢腹板I型钢梁的截面图可知,上、下翼板关于oy轴上下对称,扭转中心必在oy上,即扭转中心的z坐标为0,所以只需求得ay就可以知道扭转中心的精确位置。
IyωB=∫AωBzdA可以利用ωB图与z图图乘求得,Iy=∫Az2dA可以由z图自乘求得,将二者代入(1)式,可求得:
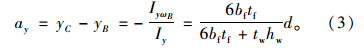
计算结果表明扭转中心的y坐标为位于从B点沿y轴正方向距离为ay处,至此参阅文献[11]就可以求得以扭转中心C为极点的主扇性惯性矩Iω,见式(4):

注意到,在式(3)中,由于波形钢腹板波高的变化,变化范围为0≤d≤dmax,使得波形钢腹板I型钢梁的扭转中心也随着波高的变化而变化,因此本文在计算ay时,d的取值关系到扭转中心计算的准确性。定义dave为最终带入方程(3)的合理波高,本文给出的计算公式为:

如图 6所示波形钢腹板平板与斜板与坐标轴ox所围的面积是由3部分组成(由于波形对称,取半个波形研究),两个三角形面积与一个四边形的面积,利用式(5)可以求得合理波高为式(6)所示:


|
| 图 6 波形钢腹板与坐标轴所围面积划分个数 Fig. 6 Partition number of area enclosed by corrugated steel webs and coordinate axis |
参阅文献[12]可知,对于纯弯状态的平腹板I型钢梁而言,在两端简支的情况下,其弯扭屈曲临界弯矩Mfcr为:

对于纯弯状态的波形钢腹板I型钢梁,在两端简支的情况下的弯扭屈曲临界弯矩Mccr参考式(7),可得式(8),


3 波形钢腹板I型钢梁弹性弯扭屈曲临界荷载公式验证
波形钢腹板I型钢梁的有限元模型采用ANSYS三维有限元软件建立,有限元模型采用shell63壳单元。梁端弯矩的施加通过在上、下翼板分别施加大小相同的均匀拉、压力实现,如图 7所示。本文研究的波形钢腹板I型钢梁为简支边界,因此有限元模型中在点A约束x,y,z这3个方向的位移及绕x轴的转角;在点B约束y,z两个方向的位移及绕x轴的转角;约束上、下翼板的梁端末端即线c、线d的z向位移;约束波形钢腹板末端即线a、线b的y向位移。

|
| 图 7 波形钢腹板I型钢梁边界与加载图 Fig. 7 Boundary and loading of I-girder with corrugated webs |
为了验证ANSYS有限元模型分析的正确性与计算精度,首先选自文献[5]一平腹板I型钢梁进行验证,钢梁的弹性模量E为206 GPa,泊松比υ取为0.3,对比分析了其ANSYS有限元计算结果与本文公式(7)计算的理论值,对比结果见表 1。平腹板I型钢梁的尺寸与有限元模型分别见表 1和图 8。

|
| 图 8 平腹板I型钢梁有限元模型 Fig. 8 FEA model of I-girder with flat webs |
| tw/mm | hw/mm | bf/mm | tf/mm | L/mm | ANSYS/ (kN·m-1) | 理论值/ (kN·m-1) | 误差 φ1/% |
| 12 | 2 000 | 500 | 40 | 15 600 | 7 548.2 | 7 795.0 | 3.3 |
 | |||||||
由表 1的结果可知,平腹板I型钢梁的有限元值与理论值的误差很小,说明有限元的边界、弯矩等效加载及网格划分满足求解精度要求,因此可以将平腹板I型钢梁的边界、弯矩等效加载及网格划分应用到波形钢腹板I型钢梁的有限元分析中。
采用文献[5]中的5片波形钢腹板I型钢梁进行分析,波形钢腹板I型钢梁与上述平腹板I型钢梁的材料属性相同,波形钢腹板I型钢梁的编号与尺寸见表 2。
| 模型 编号 | a/ mm | b/ mm | dmax/ mm | θ/ (°) | tw/ mm | hw/ mm | bf/ mm | tf/ mm | L/ mm |
| C1 | 330 | 270 | 25 | 10.5 | 12 | 2 000 | 500 | 40 | 15 600 |
| C2 | 330 | 270 | 50 | 20.3 | 12 | 2 000 | 500 | 40 | 15 600 |
| C3 | 330 | 270 | 100 | 36.5 | 12 | 2 000 | 500 | 40 | 15 600 |
| C4 | 330 | 270 | 125 | 42.8 | 12 | 2 000 | 500 | 40 | 15 600 |
| C5 | 330 | 270 | 175 | 52.4 | 12 | 2 000 | 500 | 40 | 15 600 |
5片波形钢腹板I型钢梁的ANSYS有限元计算值、应用本文公式(8)考虑及未考虑波形钢腹板的剪切模量修正值的对比结果见图 9。由图 9可知,5片波形钢腹板I型钢梁的ANSYS有限元计算结果与本文所得公式计算结果吻合良好,验证了本文所得公式的正确性。同时可以看出,随着波高dmax的增加,波形钢腹板I型钢梁的弹性弯扭屈曲临界荷载也呈增加趋势。对于本文的5片波形钢腹板I型钢梁,未考虑波形钢腹板剪切模量修正的值要大于考虑波形钢腹板剪切模量修正的值及ANSYS有限元计算值,实际计算中应考虑波形钢腹板剪切模量修正,否则会增加计算误差。

|
| 图 9 不同计算方法所得的波形钢腹板I型钢梁弹性弯扭屈曲临界荷载值 Fig. 9 Critical load of elastic flexural-torsional buckling on I-girder with corrugated webs obtained by different methods |
根据本文的研究成果,可得出以下结论:
(1)本文以开口截面薄壁杆件的约束扭转理论为基础,推导出波形钢腹板I型钢梁约束扭转时扭转中心的精确位置,并求得以扭转中心为极点的主扇性惯性矩计算公式。
(2)由于波形钢腹板的特殊构造,波高沿梁的纵向变化,为了合理计算主扇性惯性矩,本文给出了合理波高的计算公式,并在此基础上给出了波形钢腹板I型钢梁的弹性弯扭屈曲临界荷载的计算公式。
(3)文中5片波形钢腹板I型钢梁的ANSYS有限元计算结果与本文所得公式计算结果吻合良好,验证了本文所得公式的正确性。5片波形钢腹板I型钢梁在只有波高变化的情况下,随着波高的增加,其弹性弯扭屈曲临界荷载也呈增加趋势。
(4)文中5片波形钢腹板I型钢梁在未考虑波形钢腹板剪切模量修正的情况下,计算所得的弹性弯扭屈曲临界荷载值要大于考虑波形钢腹板剪切模量修正的值及ANSYS有限元计算值,说明未考虑波形钢腹板剪切模量的修正会增加计算误差,因此实际计算中为了减小误差,应当考虑其剪切模量的修正。
| [1] | ABBAS H H,SAUSE R,DRIVER R G. Behavior of Corrugated Web I-girders under in Plane Loading [J]. |
| [2] | ELGAALY M,SESHADRI A,HAMILTON R W. Bending Strength of Steel Beams with Corrugated Webs[J]. |
| [3] | EASLEY J T,MCFLAND D E. Buckling of Light-gauge Corrugated Metal Shear Diaphragms [J]. Journal of the Structural Division, 1969,95(ST7):1497-1516. |
| [4] | ELGAALY M,HAMILTON R W,SESHADRI A. Shear Strength of Beam with Corrugated Webs[J]. |
| [5] | MOON J,YI J W,CHOI B H,et al. Lateral Torsional Buckling of I-girder with Corrugated Webs under Uniform Bending[J]. |
| [6] | 陈宜言.波形钢腹板预应力混凝土桥设计与施工[M].北京:人民交通出版社,2009. CHEN Yi-yan. Design and Construction of Prestressed Concrete Bridge with Corrugated Steel Webs[M].Beijing:China Communications Press,2009. |
| [7] | 狄谨,周绪红,孔祥福,等.波形钢腹板预应力混凝土组合箱梁试验[J].长安大学学报:自然科学版,2009,29(5):29-33. DI Jin,ZHOU Xu-hong,KONG Xiang-fu,et al. Experimental Research on Pre-stressed Concrete Composite Box Girders with Corrugated Steel Webs[J]. Journal of Chang'an University:Natural Science Edition,2009,29(5):29-33. |
| [8] | 张永健,黄平明,狄谨,等. 波形钢腹板组合箱梁自振特性与试验研究[J].交通运输工程学报,2008,8(5):76-80. ZHANG Yong-jian,HUANG Ping-ming,DI Jin,et al. Free Vibration Characteristics and Experiment Study of Composite Box Girder with Corrugated Steel Webs[J]. Journal of Traffic and Transportation Engineering,2008,8(5):76-80. |
| [9] | 陈海波,刘保东,任红伟. 波纹钢腹板混凝土箱梁动力特性研究[J].公路交通科技,2007,24(2):80-83. CHEN Hai-bo,LIU Bao-dong,REN Hong-wei. Research on Dynamic Characteristic of Concrete Box-girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development,2007,24(2):80-83. |
| [10] | 尹航,刘保东,任红伟.波形钢腹板混凝土箱梁的动力特性分析[J].工程抗震与加固改造,2008,30(2):29-32. YIN Hang,LIU Bao-dong,REN Hong-wei. Analysis of the Dynamic Characteristic of Concrete Box-girders with Corrugated Steel Webs[J]. Earthquake Resistant Engineering and Retrofitting,2008,30(2):29-32. |
| [11] | 包世华,周坚. 薄壁杆件结构力学[M].北京:中国建筑工业出版社,2006. BAO Shi-hua,ZHOU Jian. Thin-walled Bars Structural Mechanics[M]. Beijing:China Architecture & Building Press,2006. |
| [12] | 陈骥.钢结构稳定理论与设计[M].北京:科学出版社,2006. CHEN Ji. Stability Theory and Design of Steel Structures [M]. Beijing:Science Press,2006. |
| [13] | SAMANTA A,MUKHOPADHYAY M. Finite Element Static and Dynamic Analyses of Folded Plates[J]. Engineering Structures,1999,21(3): 227-287. |
 2015, Vol. 31
2015, Vol. 31
