扩展功能
文章信息
- 魏锦辉, 任伟新
- WEI Jin-hui, REN Wei-xin
- 基于响应面方法的桥梁静动力有限元模型修正
- Static and Dynamic Bridge Finite Element Model Updating Based on Response Surface Method
- 公路交通科技, 2015, Vol. 31 (2): 68-73
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 68-73
- 10.3969/j.issn.1002-0268.2015.02.011
-
文章历史
- 收稿日期:2014-03-25
2. 郑州航空工业管理学院, 河南 郑州 450015
2. Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou Henan 450015, China
在进行桥梁结构静动力响应计算、承载力评价及健康监测等分析研究过程中,通常需要建立一个能够准确反映结构特性的基准有限元模型。然而,一方面由于结构的几何尺寸、材料特性及边界条件的不确定性,另一方面由于建模误差的影响,这样建立的结构有限元模型就很难反映结构的真实状态,使得有限元模型的理论计算值与实测值不可避免地存在偏差。因此,需要对初步建立的结构有限元模型进行修正,通过调整其相关参数,使得结构的理论计算值和实测值尽可能地吻合[1]。结构有限元模型修正中用到的实测数据可以是结构模态数据,如频率、振型和模态柔度等;也可以是静力响应,如结构的位移、转角和应变等。结构的静力特性和动力特性都是结构的基本特性,将静力和动力的测试信息结合在一起构造目标函数,可以增加用于模型修正的信息量,兼顾到结构的整体和局部特征,从而进一步增大模型修正结果的有效性与可靠性,因此,考虑到利用较多的结构信息,以获取较为全面的修正内容,近些年来,联合静动力的有限元模型修正技术越来越受到重视。宗周红[2]以静力位移与模态柔度为状态变量,利用ANSYS软件对一刚架拱桥进行了有限元模型修正,获得了较好的模型修正结果;姚昌荣[3]以结构实测静力位移与振动频率联合构造目标函数,对金沙江中坝大桥进行了模型修正;Schlune[4]利用结构的静力位移,应变和振动频率,对一拱桥进行了有限元模型修正研究;韩建平[5]通过构造结构的静力位移与频率的响应面模型,并利用实测数据对一座刚构-连续组合梁桥进行了模型修正。
然而,结构有限元模型修正是一个结构参数识别和确认的最优化过程,每一次迭代都需要调用有限元程序重新进行计算,在联合静动力进行有限元模型修正时,还需分别计算机构的静动力响应,过程较为复杂,特别是对于大型工程结构,单元数目较多,计算量大,不易于工程实际应用。响应面方法[6]作为一种函数逼近的工具,可以建立特征量与设计变量之间的近似函数关系来替代结构有限元模型,以显式的响应面模型逼近特征量与设计变量间复杂的隐式函数关系。利用响应面方法构造近似函数时无需进行复杂的推导,只需选择一些样本点即可,方法简单,使用方便,具有较强的通用性和独立性,在应用时省去了模型修正过程中有限元计算的复杂性,提高了计算效率,在有限元模型修正中已得到了应用[7, 8, 9]。
基于此,本文以常德市白马湖公园虹为工程实例,利用结构静载位移和振动频率等现场实测静动力响应,构造联合静动力的结构有限元模型修正的目标函数,在灵敏度分析的基础上先选择待修正参数,并利用响应面方法拟合结构静动力响应的代理模型。在有限元模型修正过程中,利用拟合的特征量关于设计变量的响应面模型,可同时直接计算结构的相关响应,避免了运用复杂的有限元方法分步计算结构响应,提高了算效率。通过对目标函数值的不断优化,实现了对该桥梁的静动力有限元模型的综合修正,从而得到了能够反映该桥梁真实状态的基准有限元模型。
1 桥梁概况
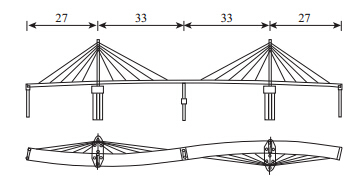
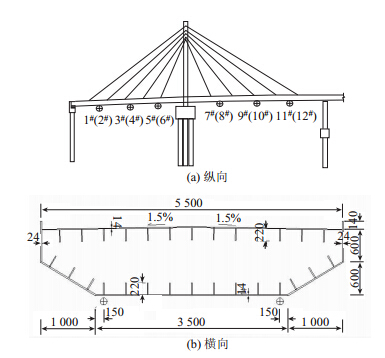
常德市白马湖公园虹桥全长120 m,为四跨曲线钢箱梁斜拉桥,跨径组合为(27+33+33+27)m,桥梁布置图和实景图见图 1和图 2。钢梁为单箱单室截面,箱梁均采用Q345qC钢,底宽3.5 m,桥面横坡1.5%,中心线处梁高1.241m,顶板和底板厚度均为0.014 m,竖腹板厚0.024 m,斜腹板厚0.020 m。顶板、底板与腹板间距约0.35~0.4m设置一道纵向加劲肋,加劲肋板厚0.016 m,肋高0.022 m,断面布置见图 3。斜拉索锚箱焊接于钢箱梁的竖腹板上,箱梁内设有横隔板,横隔板板厚分为0.02 m和0.01 m两种。本桥主塔塔高20 m,采用Q235qC钢焊接无缝钢管构造,斜拉索采用OVM成品索,型号为PES5-37。本桥作为公园景观人行天桥,设计时以主梁承受荷载为主,斜拉索横截面积及设计内力均比较小,因此实际上是一“假”斜拉桥。
|
| 图 1 斜拉桥总体布置图(单位:m) Fig. 1 General arrangement of cable-stayed bridge(unit:m) |

|
| 图 2 桥梁实景图 Fig. 2 Photograph of bridge |

|
| 图 3 斜拉桥有限元模型 Fig. 3 Finite element model of cable-stayed bridge |
根据桥梁设计图纸、结构特点及桥梁现状,并考虑荷载试验加载位置、位移测试位置及有限元修正目的,采用大型有限元程序ANSYS对该桥梁进行精细化有限元建模。如图 3所示,桥梁主梁采用Shell63单元进行模拟,其顶板、底板、腹板及加劲肋几何尺寸取设计尺寸,材料的初始质量密度为7 850 kg/m3,弹性模量取206 GPa;主塔采用Beam188进行模拟,几何尺寸取设计尺寸,材料参数初始值取为与主梁一致;拉索采用Link8进行模拟,横截面积为7.26×10-4m2,弹性模量取为195 GPa;全桥共划分44 290单元,36 605个节点,模型较为复杂。 3 现场静动力试验
在桥梁竣工之后按照荷载试验的相关标准对该桥梁进行了现场静动力试验。静力试验分为两个工况:工况一为第1跨跨中截面最大正弯矩;工况二为第2跨跨中截面最大正弯矩。本次试验采用以水箱加载的方式进行,并采用数显千分表和水准尺对试验跨进行挠度观测,挠度测点布置如图 4所示,纵向分别布置于试验跨L/4跨截面、跨中截面、3L/4跨截面,横向布置于距梁底边缘0.15 m的位置,每个截面在梁底布置两个测点,共12个位移测点;动力试验主要利用环境激励方法测试结构的振动频率,测点横向布置于主梁两侧,纵向布置于斜拉索所处的位置附近,采样频率200 Hz,采样时长10 min,运用土木工程结构模态分析软件MACES对该桥进行模态分析,获得桥梁的前5阶竖向振动频率。桥梁静动力测试结果见表 2和表 3。
|
| 图 4 挠度测点布置图(单位:mm) Fig. 4 Layout of deflection measuring points(unit:mm) |
目前,参数型修正方法已经成为结构有限元模型修正研究的主流,而结构有限元模型修正也面临着一个重要问题即修正参数的选取问题,这对结构模型修正效果有着很大的影响。为了获得良好的模型修正结果,避免因病态方程的存在而使部分修正参数变化过大而产生计算问题,需要从潜在的修正参数中挑选出尽可能少的参数以进行修正,且运用的指标对所选参数应具有足够的灵敏度[10, 11]。
对于本文斜拉桥,其主梁为由不同厚度型钢组成的全焊钢箱梁,为了获得明确的具有实际物理意义与几何意义的桥梁参数,本桥可以修正的潜在相关参数可以选择为主梁的质量密度和弹性模量、拉索弹性模量、主塔弹性模量以及组成主梁的型钢的不同厚度。由于这些参数较多,且其对于指标的灵敏度大小不确定,因此,为了保证修正结果的可靠性,对这些潜在的参数进行灵敏度分析,筛选出较少且灵敏度相对较大的参数作为待修正参数,以进行后续的有限元模型修正。对于结构体系离散化为有限元模型后,假设含有n个模型参数p1,p2,…,pn,结构的响应则为这些参数的隐式函数,可写为:
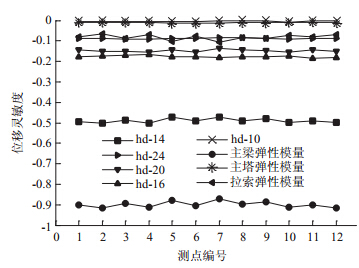
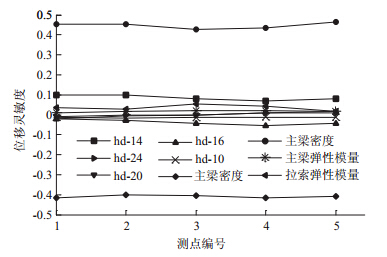
图 5和图 6为根据公式(2)计算出的各指标对相关参数的相对灵敏度值,其中“hd-X”为各指标对组成主梁厚度为X型钢的灵敏度值。从图 5中可以看出,各测点位移对主梁弹性模量均具有较高的灵敏度,而厚度分别为14,16和20 mm的型钢由于对主梁刚度贡献比较大,因此其位移灵敏度也相对较大;图 6中频率灵敏度比较大的参数为主梁弹性模量与质量密度。本桥虽为斜拉桥,但其作为人行景观天桥实则为一“假”斜拉桥,从灵敏度图中也可以看出,拉索和主塔对桥梁的响应影响并不大。综合起来,针对本桥选择相对灵敏度值大于0.1的参数作为待修正参数,分别为hd-14,hd-16,hd-20主梁密度与主梁弹性模量共5个参数。
|
| 图 5 各参数位移灵敏度分析 Fig. 5 Displacement sensibilities to different parameters |
|
| 图 6 各参数频率灵敏度分析 Fig. 6 Frequency sensibilities to different parameters |
由于本桥所建的精细有限元模型单元数较多,重分析过程较为复杂,可考虑采用响应面代理模型替代相应的有限元模型。基于试验设计的响应面法就是根据研究对象的特点,在试验设计的基础上,用多项式或其他响应面模型近似描述设计变量和响应特征之间的复杂关系,得到响应特征的响应面模型,利用该模型来预测非试验点的响应值。实际中根据工程经验,通常选取二次多项式形式的响应面模型,其数学表达式为:
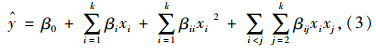
中心复合设计(CCD)作为一种试验设计方案,在响应面拟合时得到广泛的应用,然而,对于全因子中心复核设计,当输入参数增加时,需要大量增加试验样本数,这也会大大提高计算成本。因此,在保证有足够拟合精度的基础上,为减少计算量,可以采用部分因子的中心复核设计方案构造样本点。本文通过灵敏度分析方法共选择了5个参数作为待修正参数,采用25-1析因设计方法[6]进行中心复核设计,并增加了中心点的样本数,其响应面拟合的试验设计方案见表 1。其中,x1,x2,x3,x4,x5分别为hd-14型钢厚度、hd-16型钢厚度、hd-20型钢厚度、主梁密度和主梁弹模;-1和1分别代表对设计参数降低10%和提高10%。通过对试验点进行数值拟合,得到所需位移与频率响应关于这些参数的代理响应面模型。
| 样本 | 输入参数 | 样本 | 输入参数 | |||||||||
| x1 | x2 | x3 | x4 | x5 | x1 | x2 | x3 | x4 | x5 | |||
| 1 | -1 | -1 | -1 | -1 | 1 | 16 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | -1 | -1 | -1 | -1 | 17 | -2 | 0 | 0 | 0 | 0 | |
| 3 | -1 | 1 | -1 | -1 | -1 | 18 | 2 | 0 | 0 | 0 | 0 | |
| 4 | 1 | 1 | -1 | -1 | 1 | 19 | 0 | -2 | 0 | 0 | 0 | |
| 5 | -1 | -1 | 1 | -1 | -1 | 20 | 0 | 2 | 0 | 0 | 0 | |
| 6 | 1 | -1 | 1 | -1 | 1 | 21 | 0 | 0 | -2 | 0 | 0 | |
| 7 | -1 | 1 | 1 | -1 | 1 | 22 | 0 | 0 | 2 | 0 | 0 | |
| 8 | 1 | 1 | 1 | -1 | -1 | 23 | 0 | 0 | 0 | -2 | 0 | |
| 9 | -1 | -1 | -1 | 1 | -1 | 24 | 0 | 0 | 0 | 2 | 0 | |
| 10 | 1 | -1 | -1 | 1 | 1 | 25 | 0 | 0 | 0 | 0 | -2 | |
| 11 | -1 | 1 | -1 | 1 | 1 | 26 | 0 | 0 | 0 | 0 | 2 | |
| 12 | 1 | 1 | -1 | 1 | -1 | 27 | 0 | 0 | 0 | 0 | 0 | |
| 13 | -1 | -1 | 1 | 1 | 1 | 28 | 0 | 0 | 0 | 0 | 0 | |
| 14 | 1 | -1 | 1 | 1 | -1 | 29 | 0 | 0 | 0 | 0 | 0 | |
| 15 | -1 | 1 | 1 | 1 | -1 | 30 | 0 | 0 | 0 | 0 | 0 | |
本文运用实测的静力位移与振动频率,采用联合静动力的方法对该斜拉桥进行有限元模型修正,其模型修正的优化目标函数定义为:
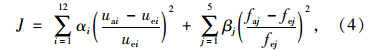
利用MATLAB程序编程对目标函数进行优化计算,优化方法采用软件自带优化工具箱fmincon函数;同时,计算理论响应时利用响应面代理模型进行计算,避免了模型修正过程中进行复杂的有限元计算,大大提高了计算效率。同时,为了体现联合静动力方法进行有限元模型修正的优越性,本文分别只应用静力位移(方法1)和振动频率(方法2)进行有限元模型修正,与联合静动力(方法3)的修正方法进行比较。
表 2和表 3分别列出了运用不同方法修正前后与实测的静力位移及振动频率的比较。对比表 2和表 3可以看出,修正前桥梁的理论计算位移值都较实测位移值大,大部分控制在8%到15%之间,第1阶和第3阶竖向反对称振动频率值与实测值误差较大,而其他3阶频率误差很小。利用方法1修正后,模型静力位移的计算值与实测值误差大为减小,控制在7%之内,但振动频率总体误差并没有得到明显改善;同样,利用方法2进行修正后,结构的振动频率总体误差减小,静力位移也得到改善,但效果有限,没有利用方法1得到的结果好;利用本文出的基于静动力的模型修正方法(方法3)修正后,与方法1得到的静力位移比较接近,同时与方法2得到的振动频率也比较接近,结构的静力位移与实测频率误差均大大改善,基本体现了单纯利用静力或动力修正方法的优点,但又避免了其不足之处,修正内容更为全面,结果更为可靠。由此表明,进行静动力有限元模型修正后,该桥静力位移以及振动频率的计算值与实测值的总体吻合程度更好,经过修正后的有限元模型基本能够反映该斜拉桥的静动力特性,可以作为该桥的基准有限元模型。
| 工况 | 测点 编号 | 实测值 /mm | 计算值/mm | 误差/% | ||||||
| 修正前 | 方法1 | 方法2 | 方法3 | 修正前 | 方法1 | 方法2 | 方法3 | |||
| 工况一 | 1 | 5.03 | 5.583 | 5.050 | 5.443 | 5.049 | 11.0 | 0.4 | 8.2 | 0.4 |
| 2 | 5.68 | 5.922 | 5.347 | 5.770 | 5.346 | 4.3 | -5.9 | 1.6 | -5.9 | |
| 3 | 6.78 | 7.761 | 7.026 | 7.567 | 7.024 | 14.5 | 3.6 | 11.6 | 3.6 | |
| 4 | 7.55 | 8.238 | 7.442 | 8.028 | 7.440 | 9.1 | -1.4 | 6.3 | -1.5 | |
| 5 | 4.06 | 4.674 | 4.240 | 4.560 | 4.239 | 15.1 | 4.4 | 12.3 | 4.4 | |
| 6 | 4.47 | 5.018 | 4.538 | 4.891 | 4.537 | 12.3 | 1.5 | 9.4 | 1.5 | |
| 工况二 | 7 | 5.86 | 6.512 | 5.910 | 6.354 | 5.908 | 11.1 | 0.9 | 8.4 | 0.8 |
| 8 | 6.53 | 6.931 | 6.272 | 6.758 | 6.270 | 6.1 | -4.0 | 3.5 | -4.0 | |
| 9 | 9.54 | 10.252 | 9.287 | 9.998 | 9.285 | 7.6 | -2.7 | 4.8 | -2.7 | |
| 10 | 9.83 | 10.857 | 9.814 | 10.582 | 9.812 | 10.4 | -0.2 | 7.7 | -0.2 | |
| 11 | 6.07 | 6.949 | 6.287 | 6.775 | 6.285 | 14.5 | 3.6 | 11.6 | 3.5 | |
| 12 | 6.67 | 7.296 | 6.589 | 7.109 | 6.587 | 9.4 | -1.2 | 6.6 | -1.2 | |
| 模态阶数 | 实测值 | 计算值 | 相对误差/% | ||||||
| 修正前 | 方法1 | 方法2 | 方法3 | 修正前 | 方法1 | 方法2 | 方法3 | ||
| 一阶反对称 | 3.782 | 3.630 | 3.778 | 3.709 | 3.709 | -4.0 | -0.1 | -1.9 | -1.9 |
| 一阶对称 | 4.700 | 4.611 | 4.800 | 4.710 | 4.715 | -1.9 | 2.1 | 0.2 | 0.3 |
| 二阶反对称 | 6.056 | 6.056 | 6.280 | 6.180 | 6.169 | 0.0 | 3.7 | 2.1 | 1.9 |
| 二阶对称 | 6.506 | 6.538 | 6.773 | 6.670 | 6.655 | 0.5 | 4.1 | 2.5 | 2.3 |
| 三阶反对称 | 12.027 | 11.430 | 11.850 | 11.655 | 11.665 | -5.0 | -1.5 | -3.1 | -3.0 |
本文提出了一种基于响应面代理模型的桥梁静动力有限元模型修正方法,并将其成功应用到了常德市白马湖公园虹桥的有限元模型修正中,获得了良好的修正效果,并得到了更能反映该桥静动力响应的基准有限元模型。从本文的研究工作可得到如下结论:
(1)本文以静动力指标作为目标函数,运用了较全面的结构信息,获得的修正结果更能全面反映桥梁的静动力特性,比单一运用桥梁的静力响应或者动力响应获得的修正结果更为可靠。
(2)修正参数的选择是关系到有限元模型修正能否成功的关键,由于潜在的修正参数较多,为了避免相关计算问题,运用灵敏度方法分析潜在参数灵敏度值,根据经验从中挑选出尽可能少的且灵敏度较大的参数作为待修正参数是一种较为实用的方法。
(3)结构有限元模型修正过程中每一次迭代都需要调用有限元程序重新进行计算,特别是运用联合静动力进行有限元模型修正时,还需分别计算结构的静动力响应,过程较为复杂,对于大型工程结构,由于单元数目较多,计算量大,不易于工程实际应用。响应面方法作为一种函数逼近的工具,在应用时省去了模型修正过程中有限元计算的复杂性,大大提高了计算效率。
(4)运用联合静动力方法对该桥进行有限元模型修正后,该桥静力位移以及振动频率的计算值与实测值总体吻合程度更好,经过修正后的有限元模型更能全面反映该斜拉桥的静动力特性,可以作为该桥的基准有限元模型。
| [1] | FRISWELL M I,MOTTERSHEAD J E. Finite Element Model Updating in Structural Dynamics [M]. Dordrecht:Kluwer Academic Publishers,1995. |
| [2] | 宗周红,夏樟华. 联合模态柔度和静力位移的桥梁有限元模型修正方法[J].中国公路学报,2008,21(6):43-49. ZONG Zhou-hong,XIA Zhang-hua. Finite Element Model Updating Method of Bridge Combined Modal Flexibility and Static Displacement[J]. China Journal of Highway and Transport,2008,21(6):43-49. |
| [3] | 姚昌荣,李亚东. 基于静动力测试数据的斜拉桥模型修正[J].铁道学报,2008,30(3):65-70. YAO Chang-rong,LI Ya-dong. Updating of Cable-stayed Bridges Model Based on Static and Dynamic Test Data[J].Journal of the China Railway Society,2008,30(3):65-70. |
| [4] | SCHLUNE H, PLOS M, GYLLTOFT K. Improved Bridge Evaluation through Finite Element Model Updating Using Static and Dynamic Measurements[J]. |
| [5] | 韩建平,骆勇鹏. 基于响应面的刚构-连续组合梁桥有限元模型静动力修正[J]. 公路交通科技,2013,30(11):53-61. HAN Jian-ping,LUO Yong-peng. Response Surface Based Finite Element Model Updating for a Rigid Frame Continuous Composite Girder Bridge Using Static and Dynamic Test Data[J]. Journal of Highway and Transportation Research and Development,2013,30(11):53-61. |
| [6] | MYERS R H,MONTGOMERY D C. Response Surface Methodology:Process and Product Optimization Using Designed Experiments [M]. New York:Wiley Publishers,2002. |
| [7] | 任伟新,陈华斌. 基于响应面的桥梁有限元模型修正[J].土木工程学报,2008,41(12):73-78. REN Wei-xin,CHEN Hua-bin. Response-surface Based on Finite Element Model Updating of Bridge Structures [J]. China Civil Engineering Journal,2008,41(12):73-78. |
| [8] | 费庆国,张令弥,李爱群,等. 基于统计分析技术的有限元模型修正研究[J].振动与冲击,2005,24(3):23-26. FEI Qing-guo,ZHANG Ling-min,LI Ai-qun,et al. Finite Element Model Updating Using Statistics Analysis [J]. Journal of Vibration and Shock,2005,24(3):23-26. |
| [9] | FANG S E,PERERA R. Damage Identification by Response Surface Based Model Updating Using D-optimal Design [J]. |
| [10] | KIM G H,PARK Y S. An Automated Parameter Selection Procedure for Finite-element Model Updating and Its Applications [J]. Journal of Sound and Vibration,2008,309(3/4/5):778-793. |
| [11] | 范立础,袁万城,张启伟. 悬索桥结构基于敏感性分析的动力有限元模型修正[J].土木工程学报,2000,33(1):9-13. FAN Li-chu,YUAN Wan-cheng,ZHANG Qi-wei. Sensitivity-based FE Model Updating of a Suspension Bridge[J]. China Civil Engineering Journal,2000,33(1):9-13. |
| [12] | BROWNJOHN J M W,XIA P Q,HAO H, et al. Civil Structure Condition Assessment by FE Model Updating:Methodology and Case Studies [J]. |
 2015, Vol. 31
2015, Vol. 31
