混凝土路面碳纤维发热线融雪化冰研究

扩展功能

加入引用管理器

Email Alert

文章信息

张倩雯, 赵艳华, 吴智敏

ZHANG Qian-wen, ZHAO Yan-hua, WU Zhi-min

混凝土路面碳纤维发热线融雪化冰研究

Deicing Performance of Carbon Fiber Heating Wires Embedded in Concrete Pavement

公路交通科技, 2015, Vol. 31 (2): 41-48

Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 41-48

10.3969/j.issn.1002-0268.2015.02.007

文章历史

收稿日期：2014-02-10

引用本文

张倩雯, 赵艳华, 吴智敏. 混凝土路面碳纤维发热线融雪化冰研究[J]. 公路交通科技, 2015, Vol. 31 (2): 41-48. 复制到剪切板

ZHANG Qian-wen, ZHAO Yan-hua, WU Zhi-min. Deicing Performance of Carbon Fiber Heating Wires Embedded in Concrete Pavement[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 41-48. 复制到剪切板

混凝土路面碳纤维发热线融雪化冰研究

张倩雯, 赵艳华, 吴智敏

大连理工大学结构工程研究所, 辽宁大连 116024

收稿日期:2014-02-10

基金项目：国家自然科学基金项目(51121005).

作者简介: 张倩雯(1989-),女,辽宁大连人,硕士研究生.

摘要：采用有限元法分析了布置碳纤维发热线的混凝土路面融雪化冰的性能.利用ANSYS热分析模块,建立了布置碳纤维发热线的混凝土路面的有限元分析模型,通过与室内、室外混凝土板的升温试验结果对比,验证了模型和计算方法的正确性.在此基础上,根据实际气象情况,计算了在不同环境温度和风力等级下,不同发热线布置间距、不同输入功率下混凝土路面的温度-时间曲线,进而得到了不同厚度的冰层完全融化所需要的时间,可以为工程设计提供参考.

关键词：道路工程混凝土路面有限元分析融雪化冰碳纤维发热线

Deicing Performance of Carbon Fiber Heating Wires Embedded in Concrete Pavement

ZHANG Qian-wen, ZHAO Yan-hua, WU Zhi-min

Institute of Structural Engineering, Dalian University of Technology, Dalian Liaoning 116024, China

Abstract:The deicing performance of carbon fiber heating wires (CFHWs) embedded in concrete pavement is analysed by FEM. The FE analysis model of concrete pavement embedding CFHWs is established using the ANSYS thermal analysis module. By comparisons with indoor and outdoor temperature elevation tests on concrete slabs, the model and the calculation method are verified. On this basis and according to the real meteorological condition, the temperature-time responses of the concrete pavement considering different ambient temperatures, wind scales, CFHW spacings and input powers are calculated, and the time for melting the ice with different thicknesses is summarized accordingly, which can provide useful information for engineering design.

Key words: road engineering concrete pavement finite element analysis deicing carbon fiber heating wire

0 引言

路面积雪结冰会严重影响道路畅通，造成高速公路或者机场关闭，给人们出行及货物运输带来不便，严重时甚至危害人身及财产安全^[1]，因此清理道路积雪成为被广泛关注的焦点。传统的除冰雪方法主要是使用融冰盐以及人工或者机械除雪法，这些方法都具有一定局限性，为此，国内外的学者和工程师提出了一些改进的融雪化冰方法，并进行了相应的研究。

LEE等^[2]首次采用地热管法进行路面融雪，其原理是将冷凝管路中被蒸发液体所释放的汽化潜热传递到道路表面来进行融雪化冰。ZENEWITZ^[3]在报告中提到，Denver东南部的Mississippi Avenue的一座桥上通过布置红外加热灯来加热桥面，达到融雪化冰效果时系统平均耗能仅75 W/m²。EUGSTER和SCHATZMANN^[4]报告了日本用循环水泵来储存太阳能，进行融雪化冰的情况。HENDERSON等^[5]在Newark,N.J.的一座高速公路吊桥上安装了发热电缆来进行融雪化冰试验。导电混凝土是在混凝土中掺杂钢屑、钢纤维、碳纤维、石墨等导电物质，减小混凝土的电阻，并对其通电加热，来进行融雪化冰。XIE等^[6,7]进行了水泥基导电混凝土的相应研究。SHERIF和TUAN^{[8,9,10,11,12]}提出在普通混凝土中掺入钢纤维、钢屑、碳纤维和石墨等导电材料，并进行了相应的研究。同时，国内也有多名学者进行了导电混凝土的导电组分含量及导电性能等方面的研究^{[13,14,15,16,17,18,19]}。ZHAO和WU等^[20,21]提出在混凝土路面中布置碳纤维发热线进行融雪化冰，并进行了一系列的室内、室外试验研究，认为发热线间距在100 mm之内可以满足融雪化冰板面的温度均匀性要求。

总体而言，地热管法和太阳能法的建造以及管路的组装复杂且费用较高；红外加热灯法升温过于缓慢，并且受外部风向影响严重；发热电缆法的加热单元稳定性较差，同时需要消耗大量的电能；导电混凝土中导电材料的掺量很难控制并且会影响混凝土的强度。而碳纤维发热线属于新型发热材料，具有良好的电热性能和机械性能，耐久性较好，在路面铺设碳纤维发热线具有易于施工、安全可靠、节能、环保等优点,因此，对碳纤维发热线用于混凝土路面融雪化冰的研究具有重要意义。

目前国内外对碳纤维发热线用于混凝土路面融雪化冰的研究主要通过试验，但由于受到降雪季节性影响，试验研究的时间局限性较大。同时，多变的气象因素也对试验结果的稳定性产生较大影响。因此，通过有限元数值模拟进行碳纤维发热线融雪化冰研究具有重要意义。但目前该方向相关研究较少，其分析方法的可靠性也有待于进一步探讨。

本文采用有限元方法计算了布置碳纤维发热线的路面系统融雪化冰的情况。首先采用ANSYS建立有限元分析模型，并将计算结果与试验结果进行了对比。在此基础上进一步分析主要参数对融雪化冰效果的影响，最后给出大量算例，包括不同发热线布置间距、不同环境温度和风力等级条件下，不同冰层厚度时，不同输入功率，冰完全融化所需要的时间，结果可为工程设计提供参考。 1 融雪化冰有限元分析 1.1 建模

当混凝土路面中布置的碳纤维发热线通电后，碳纤维发热线可以作为混凝土板中的内热源。加热系统中的热量转换方式包括热传导、混凝土板升温蓄热、冰或雪升温蓄热及融化潜热、空气对流换热、辐射散热等。边界温度不断变化，同时混凝土大板内部的温度场随时间不断变化，所以本问题属于瞬态传热，同时还涉及冰、雪融化时的相变计算。因此有限元模拟借助ANSYS软件的热分析模块，采用PLANE55二维热实体单元，建立碳纤维发热线融雪化冰系统的有限元模型。PLANE55可作为1个具有二维热传导能力的平面或轴对称环单元使用，具有4个节点，每个节点只有1个温度自由度。基本计算模型如图 1所示。混凝土板在横向认为无限长，除了最边缘的发热线外，其他各发热线间的分布基本相同，可以将其看成周期性结构模型。选取两根发热线间二分之一部分作为研究对象，即图 1中的阴影部分。计算中使用的单元及网格划分情况如图 2所示。图中，ABFE围合的矩形部分为冰层，EFDC围合的矩形部分为混凝土。在融雪化冰分析时，雪的热力学参数并不容易确定，而冰的热力学参数相对稳定，因此可将雪按照等质量的原则换算为冰来考虑。为了兼顾计算精度和效率，模型采用不均分网格划分，在碳纤维发热线附近网格划分较密，其他部分网格较稀疏。冰层部分采用分层建模，每2 mm划分为一层，计算时认为，每层冰的温度达到0 ℃以上时即融化成为水，此后在该层内使用水的参数替换冰的参数继续计算。

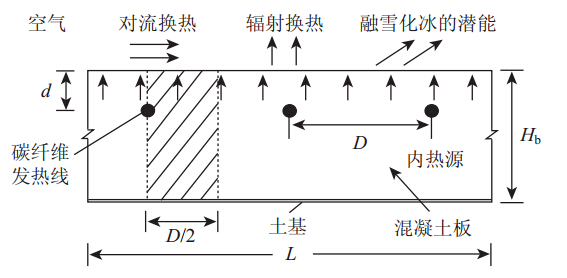
图 1 有限元分析模型Fig. 1 FE analysis model

图选项

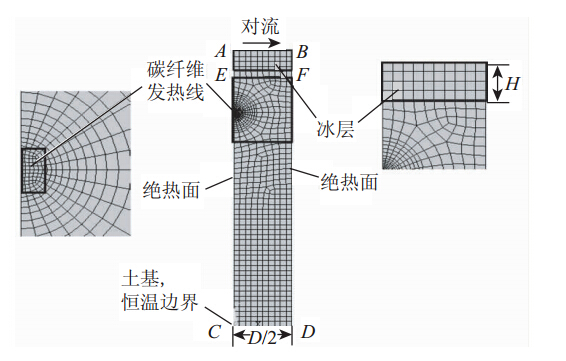
图 2 单元网格划分及边界条件Fig. 2 Element meshing and boundary conditions

图选项

在热分析中，对模型的边界条件作如下规定：如图 2所示，AC，BD面认为是绝热面；CD面与地基接触，认为是恒温边界；AB面与空气接触，存在对流换热、辐射换热等热转换，但冬季气温较低，低温条件下辐射换热较小，因此忽略该作用，在AB面上只考虑对流换热的影响。由于存在相变传热，是一个强非线性问题，需要考虑雪或冰由固相转变为液相时所吸收的潜热，ANSYS通过定义材料随温度变化的焓来考虑潜热。在等压过程中，系统焓的增加等于它所吸收的热量，焓值随温度的升高而升高，并且在-1 ℃和0 ℃附近有明显的变化，如图 3所示。在软件中考虑焓值影响时，只需输入拐点处的温度和与之对应的焓值，其余温度处的焓值将自动线性内插。

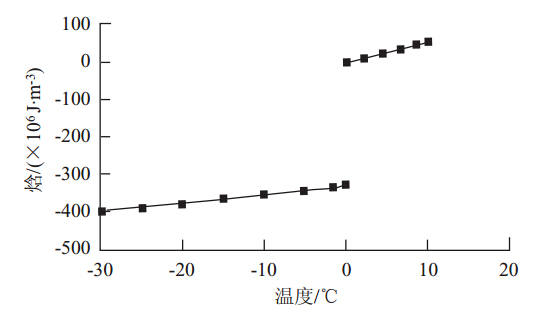
图 3 冰(水)焓值与温度的关系Fig. 3 Relationship between enthalpy value and temperature of ice (rain)

图选项

1.2 主要参数

在计算模型建立后，需要选取合理的参数。本文计算中需要的主要参数为：(1)混凝土板和碳纤维发热线的几何尺寸，由实际情况确定；(2)混凝土、冰、水及碳纤维发热线的密度、导热系数以及比热容等见表 1；(3)碳纤维发热线的输入功率，按实际情况确定；(4)冰的焓值，由图 3确定^[22]；(5)考虑风作用时的对流换热系数，风力等级与风速的关系见表 2，本文采用每级风速的平均值，对流换热系数与风速的关系由图 4 确定^[23]；(6)计算时的环境温度，按实际情况取值。当以上参数确定后，可以进行有限元计算。

表 1 材料参数 Tab.1 Material parameters

材料	密度/ (kg·m^-3)	导热系数/[W· (m·K)^-1]	比热容/[(kJ· (kg·K)^-1]	电阻/ (Ω·m^-1)
混凝土	2 500	2.34	1.046	—
冰	917	2.20	2.05	—
水	1 000	0.50	4.20	—
碳纤维发热线	2	19.03	—	16.50

表选项

表 2 风力等级与风速的关系 Tab.2 Relationship between wind scale and wind speed

风力等级/级	0	1	2	3	4	5	6
风速/ (m·s^-1)	0~ 0.2	0.3~ 1.5	1.6~ 3.3	3.4~ 5.4	5.5~ 7.9	8.0~ 10.7	10.8~ 13.8

表选项

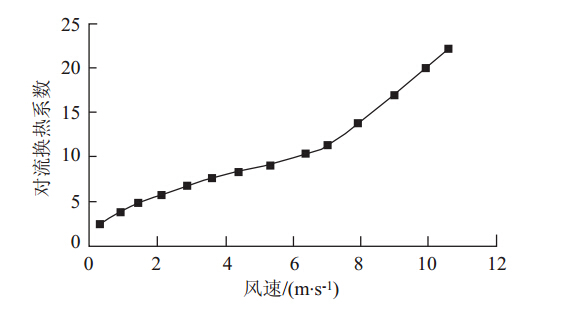
图 4 对流换热系数与风速的关系Fig. 4 Relationship between coefficient of convective heat transfer and wind speed

图选项

2 试验验证 2.1 试验基本情况

为了验证本文有限元计算的准确性，将其与试验结果进行对比验证。试验^[24]分为混凝土板升温及化冰两部分，采用的混凝土板基本参数见表 3。试验中实时监控了气温、风速以及埋置碳纤维发热线的混凝土板的温度变化情况。碳纤维发热线直径为6.5 mm。

表 3 混凝土板尺寸、发热线间距及埋深 Tab.3 Dimensions of concrete slab,spacing and embedded depth of CFHWs

试件编号	长(L)×宽(B)/ (m×m)	板厚 H_b/ mm	发热线埋深 d/mm	发热线间距 D/mm
S1	0.4×0.2	50	25	30
S2	2×1	250	40	70
S3	2×1	250	40	100
S4	2×1	250	40	120

表选项

试验共计11组，受天气因素及降雪条件限制，设计混凝土板升温试验8组，编号SW1~SW8，分为室内试验(SW1~SW2)及室外试验(SW3~SW8)两部分；化冰试验3组，编号HB1~HB3，同样分为室内试验(HB1~HB2)及室外试验(HB3)两部分。各组试验详情见表 4。其中，HB1和HB2试验中冰层厚度为实际测量的人工制冰的厚度;HB3试验中冰层厚度为按照等质量原则将积雪厚度换算得到。对于室内试验，忽略对流换热的影响，计算时风力等级取0级。

表 4 试验工况 Tab.4 Test conditions

试验编号	参数
试验编号	使用试件	环境温度 T₀ /℃	输入功率P /(W·m^-2)	风力等级 W_G/级	升温时间 t/h	冰层厚度 H/mm
SW1	S1	15	150	0	8	—
SW2	S1	-6	500	0	8	—
SW3	S2	5	1 000	3	6	—
SW4	S3	1	1 250	4	6	—
SW5	S4	-5	800	2	6	—
SW6	S2	-3	150	1	13	—
SW7	S2	-1	150	3	5	—
SW8	S3	-4	500	2	7	—
HB1	S1	-13	500	0	3	5
HB2	S1	-18	800	0	3	5
HB3	S3	-1.8	500	2	2	5.45

表选项

2.2 结果对比

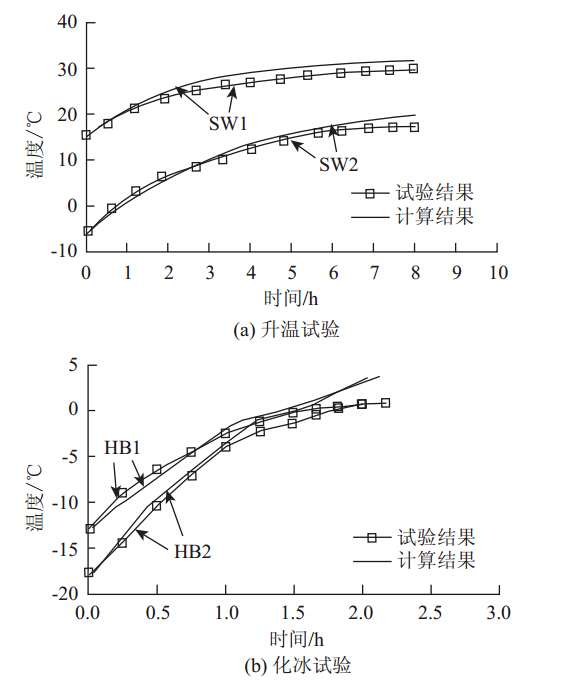
根据表 1~表 3中提供的参数，可以采用有限元模型进行计算，并与室内和室外试验结果进行对比。室内升温试验(SW1~SW2)和化冰试验(HB1~HB2)温度-时间曲线的计算与试验结果的对比分别见图 5(a)和(b)。图中的温度为板面温度的平均值。由图 5可知，针对室内试验计算的温度-时间曲线与试验结果吻合良好。这是因为室内试验过程中，环境温度、风速等变化较小，对试验结果的影响也较小。

图 5 室内试验计算与试验结果对比Fig. 5 Comparison between simulation and experimental results for indoor test

图选项

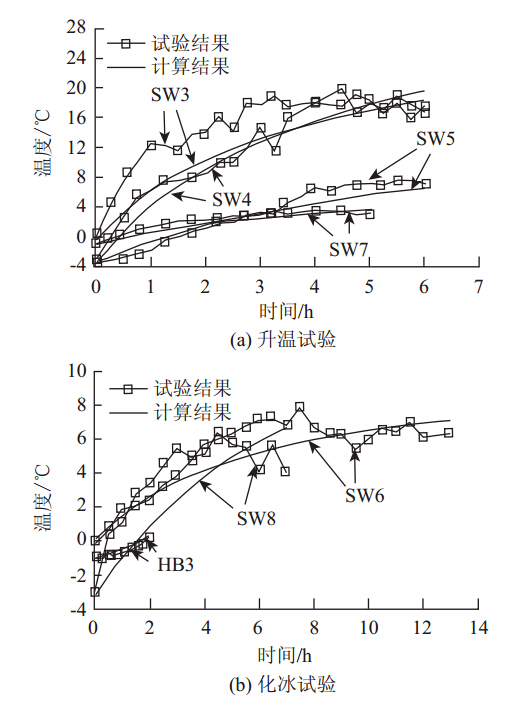
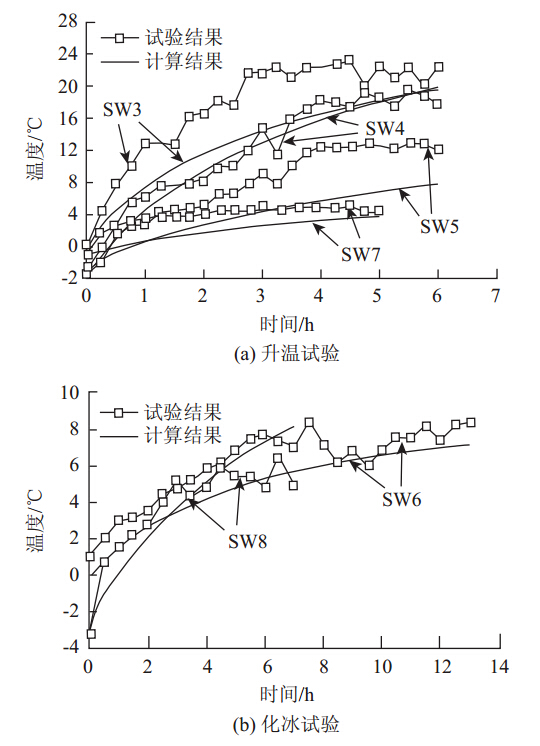
对于室外升温试验(SW3~SW8)，计算了6组试验中混凝土板面最低温度点(图 2中的F点)处和最高温度点(图 2中的E点)处的温度-时间曲线，并与试验结果进行了对比，对比结果分别见图 6(a)和图 7(a)。对于室外化冰试验(HB3)，计算了冰层表面最低温度点(图 2中的B点)的温度随时间变化的试验曲线，其与试验结果的对比见图 6(b)。

图 6 室外试验最低温度点计算与试验结果对比Fig. 6 Comparison between simulation and experimental results at location of lowest temperature for outdoor test

图选项

由图 6和图 7可知，对于室外升温试验，当碳纤维发热线通电后，混凝土板内温度开始上升。但由于风的存在，板表面存在对流换热，因此随着时间的增加，温度升高的速率逐渐降低。对于室外化冰试验，由于考虑了相变过程中焓的影响，温度在0 ℃附近增长缓慢，直到输入的总热量使冰全部融化为水后，温度才开始较大幅度的升高。对比结果发现，SW8曲线的计算与试验结果相差较大，主要因为在试验中，随着升温时间的增加，环境温度产生了较大的变化，由-3 ℃降低到-6 ℃，而在有限元模型中无法考虑外界环境温度随时间的变化，因此试验中测得的温度值相对偏低，且波动较大。在其他组试验中也发现了类似的情况，即在两个相邻时间点监测到的温度值的变化较大，温度-时间试验曲线呈折线形发展。这也说明了试验过程中很多因素，例如环境温度、风速等的变化会对试验结果产生较大的影响，从而造成计算结果与试验结果的误差。总体来说，对于室内和室外试验，有限元计算数据与试验结果均吻合良好，验证了本文模型及计算方法的正确性。

图 7 室外试验最高温度点计算与试验结果对比Fig. 7 Comparison between simulation and experimental results at location of highest temperature for outdoor test

图选项

3 混凝土路面融雪化冰的预测

3.1 计算参数的确定

采用有限元分析预测实际的路面融雪化冰情况，首先要确定合理的碳纤维发热线铺设及气象参数，再对各种参数组合进行模拟计算。根据路面工程的设计标准，为了满足特重型车辆通过的要求，水泥混凝土路面设计厚度多为220~240 mm^[25]，因此本文选用250 mm作为路面混凝土板的厚度。此外，相关研究^[24]显示，碳纤维发热线的保护层厚度在20~60 mm范围内变动对混凝土板表面温度场分布影响较小，因此本文选用40 mm作为发热线的保护层厚度。同时，当碳纤维发热线布置间距D小于100 mm时，可以满足融雪化冰板面温度均匀性的要求^[24]。为了满足不同地区对发热线布置间距的要求，本文选择了40,70和100 mm 3种间距的铺设方案进行计算。按照碳纤维发热线的使用要求，将输入功率P设定为500,1000,1500,2000,2 500 W/m² 5档。针对我国的气象特征^[26]，将冬季的环境温度、风力等级以及积雪厚度转换的冰层厚度各分为3档，详见表 5。

表 5 计算参数 Tab.5 Calculation parameters

发热线间距 D/mm	冰层厚度 H/mm	环境温度 T₀/℃	风力等级 W_G/级	输入功率 P/(W·m^-2)
40	5	-5	2	500
70	10	-15	4	1 000
100	20	-25	6	1 500
				2 000
				2 500

表选项

3.2 计算结果及分析

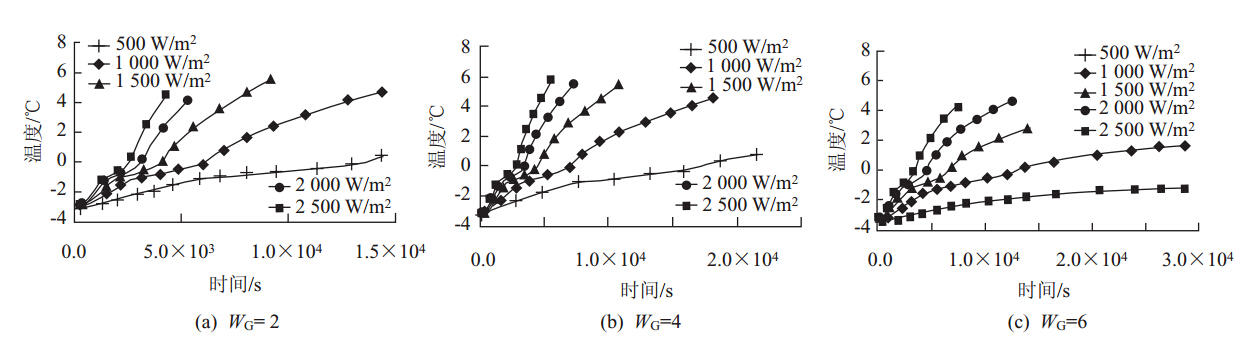
对表 5中各参数组合进行有限元模拟，计算得到405种情况下冰雪层表面温度最低点(图 2中的B点)的温度-时间曲线。图 8选取了D=100 mm，H=5 mm，T₀=-5 ℃的情况作为计算结果的典型代表。图中显示，当环境条件相同时，输入功率P越大，在相同时间内冰层表面温度越高，当温度达到0 ℃时，认为冰层被融化。温度-时间曲线的特性为：开始阶段，随着时间增加，温度呈非线性增长；当温度升高到-1 ℃左右时，温度随时间发展而增大的趋势变缓;直到达到0 ℃，温度才随时间增长而较快地提高。这是由于在计算中考虑了相变的影响，在冰融化成水的过程中只吸收热量而基本不提高温度，因此温度-时间曲线的斜率会发生改变。对比图 6(a)和(b)可知，当环境温度、冰层厚度相同时，风速也会对系统温升产生很大影响。例如，当输入功率保持在500 W/m²时，风速从2级提高到4级，使5 mm冰层融化需要的时间增加了20%。图 6(c)则表明，若风速达到6级，其他条件不变时，使用500 W/m²的输入功率已无法使冰层融化。这说明此时若要达到融雪效果，需要提高输入功率。

图 8 D=100 mm，H=5 mm，T₀=-5 ℃时的温度-时间曲线Fig. 8 Temperature-time curves (D=100 mm，H=5 mm,T₀=-5 ℃)

图选项

3.3 计算结果

405种情况下化冰所需要时间的计算结果详见图 8及表 6~表 8。对于需要使用此表的单位，可以根据碳纤维发热线布置间距以及实际降雪量选择合适的表格，再根据当前环境温度及风力等级，查询将当前积雪全部融化所需要的时间，并根据自身情况选择合理的输入功率。

表 6 D=100 mm时的化冰时间(单位：h) Tab.6 Deicing time (D=100 mm) (unit:h)

H/mm	T₀/℃	W_G/级	P/(W·m^-2)
H/mm	T₀/℃	W_G/级	500	1 000	1 500	2 000	2 500
5	-5	2	3.81	1.71	1.15	0.88	0.73
		4	4.82	1.93	1.24	0.94	0.77
		6	—	3.58	1.84	1.26	0.98
	-15	2	17.2	4.97	2.96	2.08	1.60
		4	—	7.54	3.83	2.55	1.88
		6	—	—	—	9.20	4.32
	-25	2	—	9.85	5.26	3.61	2.72
		4	—	—	8.68	5.04	3.51
		6	—	—	—	—	—
10	-5	2	4.81	2.27	1.52	1.18	0.99
		4	6.10	2.56	1.67	1.27	1.04
		6	—	4.40	2.35	1.66	1.31
	-15	2	21.18	5.86	3.54	2.55	1.98
		4	—	8.85	4.55	3.08	2.33
		6	—	—	—	10.94	5.15
	-25	2	—	11.32	6.09	4.18	3.21
		4	—	—	10.02	5.81	4.14
		6	—	—	—	—	—
20	-5	2	6.92	3.34	2.31	1.81	1.50
		4	8.64	3.71	2.47	1.91	1.58
		6	—	6.11	3.38	2.41	1.91
	-15	2	—	7.60	4.70	3.44	2.73
		4	—	11.64	5.95	4.10	3.15
		6	—	—	—	17.1	6.72
	-25	2	—	14.50	7.59	5.30	4.13
		4	—	—	12.88	7.31	5.25
		6	—	—	—	—	—
注：“—”指24 h内无法将冰层融化。

表选项

表 7 D=70 mm时的化冰时间(h) Tab.7 Deicing time (D=70 mm) (unit:h)

H/mm	T₀/℃	W_G/级	P/(W·m^-2)
H/mm	T₀/℃	W_G/级	500	1 000	1 500	2 000	2 500
5	-5	2	1.62	0.82	0.58	0.48	0.40
		4	1.83	0.89	0.62	0.50	0.41
		6	3.30	1.20	0.76	0.55	0.49
	-15	2	4.76	1.99	1.23	0.92	0.75
		4	7.13	2.42	1.43	1.02	0.81
		6	—	7.86	2.78	1.68	1.22
	-25	2	9.40	3.50	2.02	1.49	1.15
		4	—	4.80	2.60	1.78	1.30
		6	—	—	19.1	4.34	2.62
10	-5	2	2.19	1.12	0.81	0.66	0.57
		4	2.45	1.22	0.86	0.69	0.58
		6	4.20	1.58	1.10	0.80	0.64
	-15	2	5.68	2.44	1.58	1.18	0.97
		4	8.40	2.95	1.80	1.30	1.05
		6	—	9.33	3.30	2.00	1.51
	-25	2	10.83	4.08	2.50	1.75	1.42
		4	—	5.52	3.08	2.10	1.60
		6	—	—	—	4.90	3.10
20	-5	2	3.25	1.75	1.26	1.03	0.88
		4	3.60	1.85	1.32	1.06	0.91
		6	5.85	2.32	1.55	1.21	1.02
	-15	2	7.36	3.33	2.20	1.68	1.38
		4	11.10	3.98	2.49	1.86	1.50
		6	—	13.42	4.41	2.82	2.10
	-25	2	13.84	5.16	3.24	2.38	1.89
		4	—	7.03	3.99	2.80	2.17
		6	—	—	—	6.39	4.05

表选项

表 8 D=40 mm时的化冰时间(单位：h) Tab.8 Deicing time (D=40 mm) (unit:h)

H/mm	T₀/℃	W_G/级	P/(W·m^-2)
H/mm	T₀/℃	W_G/级	500	1 000	1 500	2 000	2 500
5	-5	2	0.59	0.36	0.28	0.23	0.21
		4	0.61	0.37	0.29	0.24	0.22
		6	0.74	0.41	0.31	0.26	0.23
	-15	2	1.20	0.62	0.45	0.36	0.31
		4	1.38	0.66	0.47	0.38	0.32
		6	2.62	0.91	0.58	0.45	0.38
	-25	2	2.00	0.90	0.61	0.48	0.40
		4	2.51	1.02	0.67	0.52	0.43
		6	—	1.77	0.97	0.68	0.54
10	-5	2	0.81	0.5	0.39	0.33	0.29
		4	0.85	0.51	0.40	0.34	0.29
		6	1.00	0.56	0.43	0.35	0.31
	-15	2	1.53	0.80	0.58	0.47	0.41
		4	1.75	0.86	0.61	0.49	0.43
		6	3.17	1.16	0.76	0.59	0.49
	-25	2	2.88	1.29	0.87	0.67	0.56
		4	3.71	1.49	0.96	0.73	0.60
		6	—	2.86	1.48	1.01	0.80
20	-5	2	1.25	0.78	0.61	0.51	0.46
		4	1.30	0.80	0.62	0.53	0.46
		6	1.52	0.87	0.67	0.56	0.49
	-15	2	2.16	1.17	0.86	0.71	0.61
		4	2.44	1.25	0.90	0.73	0.63
		6	4.24	1.65	1.10	0.86	0.72
	-25	2	3.16	1.56	1.09	0.86	0.74
		4	3.86	1.74	1.18	0.93	0.78
		6	—	2.88	1.65	1.21	0.98

表选项

4 结论

本文采用有限元分析软件ANSYS对碳纤维发热线融雪化冰的过程进行了模拟分析，并将计算结果与试验结果进行了对比，发现二者吻合良好，验证了模型和计算方法的正确性。在此基础上，利用建立的分析模型预测了不同碳纤维发热线间距、积雪厚度、环境温度、风力等级以及输入功率条件组合下冰雪层表面的温度-时间曲线，并据此总结了不同情况下将冰雪完全融化所需要的时间，可以为工程设计提供参考。

参考文献

[1]	方恒亮,赵茂才,张海,等.基于有限元的水泥路面冰冻损伤机理[J].公路交通科技,2011,28(8):13-18. FANG Heng-liang, ZHAO Mao-cai, ZHANG Hai, et al. Damage Mechanism of Cement Pavement under Freezing Environment Based on FEM[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 13-18.

[2]	LEE R C, SACKOS J T, NYDAHL J E, et al. Bridge Heating Using Ground-source Heat Pipes[J]. Transportation Research Record, 1984, 962: 51-56.

[3]	ZENEWITZ J A. Survey of Alternatives to the Use of Chlorides for Highway Deicing, FHWA-RD-77-52[R]. Washington, D. C.: Offices of Research and Development, Federal Highway Administration, 1977.

[4]	EUGSTER W J, SCHATZMANN J. Harnessing Solar Energy for Winter Road Clearing on Heavily Loaded Expressways[C]// Proceedings of the 6th International Winter Road Congress. Sapporo: World Road Association, 2002.

[5]	HENDERSON D J. Experimental Roadway Heating Project on a Bridge Approach[J]. Highway Research Record, 1965, 111(14): 14-25.

[6]	XIE P, BEAUDOIN J J. Electrically Conductive Concrete and Its Application in Deicing[J]. ACI Special Publication, 1995, 154(21): 399-417.

[7]	XIE P, GU P, BEAUDOIN J J. Conductive Concrete Cement-based Compositions:U.S.,5447564 [P]. 1999-4-28.

[8]	YEHIA S, TUAN C Y. Conductive Concrete Overlay for Bridge Deck Deicing[J]. ACI Materials Journal, 1999, 96(3): 382-390.

[9]	YEHIA S, TUAN C Y, FERDONETAL D. Conductive Concrete Overlay for Bridge Deck Deicing: Mixture Proportioning Optimization and Properties[J]. ACI Materials Journal, 2000,97(2): 172-181.

[10]	TUAN C Y. Electrical Resistance Heating of Conductive Concrete Containing Steel Fibers Shavings[J]. ACI Materials Journal, 2004, 101(1): 65-71.

[11]	TUAN C Y. Roca Spur Bridge: The Implementation of an Innovative Deicing Technology[J].

[12]	TUAN C Y, YEHIA S. Evaluation of Electrically Conductive Concrete Containing Carbon Products for Deicing[J]. ACI Materials Journal, 2004, 101(4): 287-293.

[13]	WANG G. Electrically Conductive Graphite Containing Concrete[J]. Chemical Abstracts, 2001, 58 (4): 57-62.

[14]	唐祖全,李卓球,侯作富,等.导电混凝土电热层布置对路面除冰效果的影响[J].武汉理工大学学报,2002,24(2):45-48. TANG Zu-quan, LI Zhuo-qiu, HOU Zuo-fu, et al. Influence of Setting of Electrical Conductive Concrete Heating Layer on Effectiveness of Deicing[J]. Journal of Wuhan University of Technology, 2002, 24(2): 45-48.

[15]	侯作富,李卓球,王建军.碳纤维水泥基复合材料电阻变化规律研究[J].武汉理工大学学报,2007,29(7):30-32. HOU Zuo-fu, LI Zhuo-qiu, WANG Jian-jun. Research on the Electrical Resistance Variation of the Carbon Fiber Cement-based Composites[J]. Journal of Wuhan University of Technology, 2007, 29(7): 30-32.

[16]	侯作富,李卓球,唐祖全.融雪化冰用碳纤维混凝土的导电性能研究[J].武汉理工大学学报,2002,24(8):32-34. HOU Zuo-fu, LI Zhuo-qiu, TANG Zu-quan. Study on Electrical Properties of Carbon Fiber Electrically Conductive Concrete for Deicing or Snow-melting[J]. Journal of Wuhan University of Technology, 2002, 24(8): 32-34.

[17]	唐祖全,李卓球,侯作富,等.导电混凝土电热除冰化雪的功率分析[J].重庆建筑大学学报,2002,24(3):101-105. TANG Zu-quan, LI Zhuo-qiu, HOU Zuo-fu, et al. Power Analysis on Deicing and Snow Melting by Electrically Conductive Concrete[J]. Journal of Chongqing Jianzhu University, 2002, 24(3): 101-105.

[18]	朱四荣,李卓球,宋显辉,等.PAN基碳纤维毡的电热性能[J].武汉理工大学学报,2004,26(9):13-16. ZHU Si-rong, LI Zhuo-qiu, SONG Xian-hui, et al. The Electro-thermal Feature of PAN-based Carbon Fiber Mat[J]. Journal of Wuhan University of Technology, 2004, 26(9): 13-16.

[19]	LI H, ZHANG Q, XIAO H. Self-deicing Road System with a CNFP High-efficiency Thermal Source and MWCNT/cement-based High-thermal Conductive Composites[J]. Cold Regions Science and Technology, 2013, 86(2): 22-35.

[20]	ZHAO H, WU Z, WANG S, et al. Concrete Pavement Deicing with Carbon Fiber Heating Wire[J].

[21]	ZHAO H, WANG S, WU Z, et al. Concrete Slab Installed with Carbon Fiber Heating Wire for Bridge Deck Deicing[J].

[22]	FEISTEL R, WAGNER W. A New Equation of State for H₂O Ice IH[J].

[23]	CHAPMAN A J. Heat Transfer[M]. New York: McGraw-Hill, 1984.

[24]	赵宏明.布置碳纤维发热线的混凝土路面及桥面融雪化冰试验研究[D].大连:大连理工大学,2010. ZHAO Hong-ming. Experimental Investigation on Concrete Pavement and Bridge Deck Deicing with Carbon Fiber Heating Wire[D]. Dalian: Dalian University of Technology, 2010.

[25]	侯作富.融雪化冰用碳纤维导电混凝土的研制及应用研究[D].武汉:武汉理工大学,2003. HOU Zuo-fu. Research on Making and Application of Carbon Fiber Electrically Conductive Concrete for Deicing and Snow-melting[D]. Wuhan: Wuhan University of Technology, 2003.

[26]	管数园.电缆加热系统进行融雪的数值分析研究[D].上海:上海交通大学,2008. GUAN Shu-yuan. A Simulation Study of Electric Cable Heating System Used in De-snowing[D]. Shanghai: Shanghai Jiaotong University, 2008.