扩展功能
文章信息
- 郭为强, 魏亚
- GUO Wei-qiang, WEI Ya
- 水泥混凝土路面板硬化过程中温度分布实测与模拟
- Measurement and Simulation of Temperature Distribution in Cement Concrete Pavement Slab during Hardening Process
- 公路交通科技, 2015, Vol. 31 (2): 33-40
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (2): 33-40
- 10.3969/j.issn.1002-0268.2015.02.006
-
文章历史
- 收稿日期:2014-04-04
水泥混凝土路面板因温度翘曲变形受到约束而产生的内应力称作翘曲应力,有时可以达到相当大的程度,成为导致路面板断裂的主要因素。而影响翘曲应力大小的,除了板的尺寸及板和地基的相对刚度外,主要取决于板顶和板底之间的温度梯度。近年来的研究成果证实,混凝土路面板硬化过程中温度发展和固化温度梯度会在路面板的生长初期形成残余应力和固化翘曲,进而对路面板的平整度、脱空和断板等长期性能有显著影响[1]。有研究结果表明,在路面板铺筑以后的24~72 h,混凝土的温度发展对路面长期性能会产生重大影响。尤其在高温炎热的天气条件下铺筑的路面,混凝土板内的温度控制对提高水泥混凝土路面的耐久性至关重要[2]。
国内外学者对混凝土路面板的温度分布情况进行过长期实测和研究[3,4,5],积累了大量数据。但是,现场实测不仅耗费人力物力而且需要在道路施工阶段同时进行,相比之下,数值模拟更加方便,可以选取不同的参数反复进行。因此,准确可靠的温度模拟程序可以系统、高效地得到硬化过程中混凝土路面温度分布和温度梯度数据,为进一步研究提供基础。国外针对水泥混凝土路面温度场模拟分析的专业软件较多,有的已经应用较成熟。国内,张君[6]等为了考察路面板在不同季节、不同浇注时间的温度场变化情况,基于绝热温升试验和有限差分方法,建立了考虑水泥水化放热与环境作用的混凝土路面板温度场计算模型;胡昌斌[7]等研究分析了水泥混凝土路面早龄期温度场特征并选取模型参数,采用有限差分法编制了水泥混凝土路面早龄期温度场数值模拟程序,通过现场监测试验验证了程序并进行了参数敏感性分析。
路面板因为暴露在外界自然环境中,除了硬化过程中水化反应释放热量以外,环境因素变化复杂,外部环境可能是一个额外的热源,也可能低于路面温度而从中吸收热量。路面板与外部环境不断发生热量的交换,板内温度变化是各种热流量不断平衡的结果。在水化反应和热交换过程影响下材料的热物理参数不是固定的常数,而变化的热物理参数又将影响到温度分布和水化进程,这些相互作用关系需要研究考虑。本文选取位于我国公路一级区划西南潮暖区的一段试验路段,对路面板早期温度分布进行实测和模拟,建立的水化模型和路面温度场预测模型对于水泥混凝土材料具有普遍适用性。 1 硬化混凝土路面板内温度分布测量
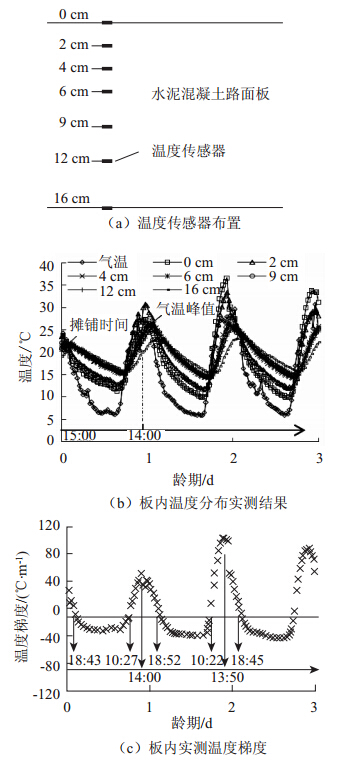
本研究选取试验路段位于我国公路一级区划西南潮暖区。在试验路段埋设温度传感器,位于道路中央。道路中央位置的温度场符合沿深度方向的一维热传导条件,实测数据用于和模拟值进行对比验证。图 1(a)给出了温度传感器沿路面板深度方向的布置情况,板厚16 cm,在0 cm(板表),2,4,6,9,12,16 cm(板底)深度处布置温度传感器,从水泥混凝土路面铺筑(下午15∶00)以后开始记录温度数据,数据自动采集时间间隔为30 min。
|
| 图 1 路面板内温度传感器布置和温度实测结果Fig. 1 Locations of temperature sensors and measured values in pavement concrete slab |
路面板不同深度处的温度数据采集结果如图 1(b)所示。由图可以看出:(1)路面板内的温度随气温和太阳辐射的昼夜变化呈现周期变化。从时间上来看,气温的变化滞后于太阳辐射,板顶温度的变化与气温几乎是同步周期性变化,而板内的温度变化滞后于板顶。在一天内,太阳辐射的峰值时间出现在中午12∶00左右,气温的最大峰值时间在中午14∶00左右,滞后太阳辐射约2 h。(2)本试验路段铺筑后的前3天,路表处温度日变化幅度达到26 ℃,路表下9 cm 处温度日变化幅度为15 ℃,路表下16 cm处(板底)温度日变化幅度为9 ℃,气温的最大日变化幅度为23 ℃。由此可见,路表的温度日变化幅度稍大于气温的日变化幅度,而在板内,随着深度增加,温度日变化幅度逐渐减小。
路面板内实测温度梯度结果如图 1(c)所示。由图可以看出:(1)前72 h内的最大正温度梯度出现在每天中午14∶00左右,这也是气温峰值和板顶温度峰值对应的时间点。(2)一天内温度梯度为0的两个时间点在上午10∶30和晚上19∶00附近。在路面混凝土板的整个硬化过程中,这3个特征时间点较为稳定,并没有因为外界环境以及早龄期复杂的物理化学作用、热交换进程而波动太大,始终保持规律性。 2 温度场数值模拟 2.1 理论模型
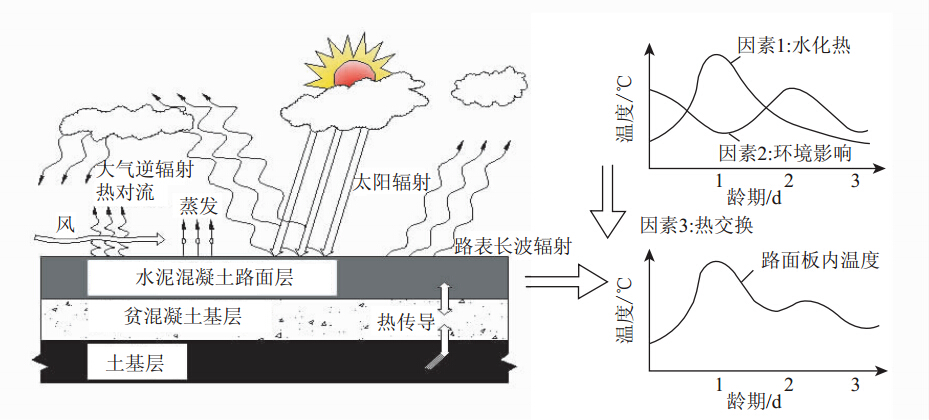
水泥混凝土路面在铺筑以后,胶凝材料的水化反应过程会释放出热量。在路面板与外界自然环境之间也会发生热量的交换:在白天由于太阳辐射作用,路面周围环境是一个外部的热源;在晚上气温大幅下降,环境温度通常会低于板内温度而从路面板中吸收热量。因此,水泥混凝土的温度变化是各种热流量不断平衡的结果。图 2是路面板内温度场形成变化示意图。
|
| 图 2 引起板内温度场变化的主要因素Fig. 2 Influencing factors of temperature field change in slab |
如图 2所示,硬化过程中路面板温度场的变化由水化热、环境变化、热交换3个方面的作用组成。(1)水化热:混凝土水化是一个放热过程。很多因素会影响混凝土水化热总量和释放速率,并且这些因素之间的相互作用关系是非常复杂的。水化环境温度、水泥用量、水灰比、水泥化学组分、水泥细度、矿物掺和料和化学外加剂用量都会影响水化放热过程。(2)环境变化:与绝大多数化学反应一样,环境的温度和湿度对于混凝土水化过程有强烈影响。太阳辐射、云层状况、大气温度、风速、降雨量、相对湿度等都是不断变化的外界因素。白天路面板内温度的升高主要是由较高的太阳辐射值引起,夜晚温度的降低则是由大气环境温度下降引起。(3)热交换:路面板与外界环境之间一直处于一种非稳态的热量交换状态,需要用热传导理论来考虑这种瞬态的热交换。在道路硬化过程中,水化程度、温湿度等因素会影响混凝土的热物理参数,进而控制板内的热传导过程。风速和气温等环境因素也决定着路表和空气之间的热对流情况。因此,上述3大因素之间存在着较复杂的互相作用关系,共同决定了实际的板内温度发展。
下面介绍上述3个方面的模型研究和参数选取。 2.1.1 水化热模型
在化学反应过程中,温度对化学反应速率的影响服从Arrhenius方程。一般来说,化学反应的速率会随着温度的升高而加快。Bazant根据Arrhenius方程提出了成熟度函数[8],该函数被用来计算参考温度。在等效龄期方法中,任意一个反应温度下的时间间隔可以转换为一个参考温度(20 ℃)下的等效时间间隔。
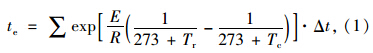
在Arrhenius方程和成熟函数中,活化能定义为水化反应的温度敏感度。Schindler测定了水化过程在4.4~40.6 ℃温度范围内的活化能,提出了活化能E的数学表达式[9],如式(2)所示。这个活化能模型在数值上直接由水泥化学组分计算求得,独立于养护温度,与瑞典化学家Arrhenius的化学反应过程速率理论一致。
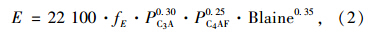
基于普通水泥的每一种成分都有一个固定的水化热值,单位质量水泥的总水化热值(Hu)可以直接通过水泥组分比例计算得到。而针对水化热的释放过程研究,通常用已经释放的水化热量除以最终释放的总水化热量来定义一个水化度。很多研究者测定了水化度曲线,提出各种数学拟合模型。本文采用Schindler提出的水化度数学模型[9],如式(3)的指数模型,能够精确拟合水化度发展的S形曲线。其中,水化度曲线的3个参数可以通过绝热温升试验数据按式(3)回归得到[10]。
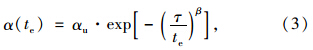
综合以上各水化模型,水化反应的放热速率QH与水化程度有关,而水化度是时间和温度历程的函数,可以用等效龄期的方法来表示。将实际龄期通过等效龄期转换后得到在te时刻的水化放热速率的表达式如式(4)所示。
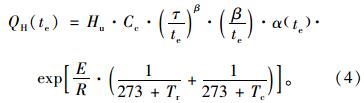
对于一种具体的水泥类型和混凝土配比,式(4)中的总水化热、活化能和水化度曲线三参数都是确定的,因而,只有时间和温度历程决定着实际龄期t时刻的水化放热速率,即热传导方程的中的内热源一项。采用式(4)计算水化放热速率,对于温度模拟程序的编制是方便且精确的。 2.1.2 环境模型
气温和太阳辐射是影响路面板内混凝土水化过程和温度发展的主要外部环境因素,且两者都是以昼夜为周期变化。 2.1.2.1 气温
同济大学严作人等[11]采用两个正弦函数的线性组合得出的气温日变化过程模拟函数,数学表达式见式(5):
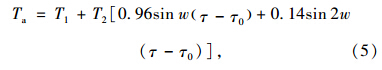
采用双参数三角函数的气温计算模型,正常天气下模拟值和实际值误差通常较小,且只需要日平均气温和日气温振幅两个参数就可以模拟一天内的气温变化,计算较为简便,便于工程使用。 2.1.2.2 辐射
太阳辐射以热流的形式从路面板顶部进入板内,是白天板内温升的主要原因。除太阳直接辐射外,路面板接受的辐射还有大气散射以及大气长波辐射,同时路面板自身也会向外放出长波辐射。
一天内太阳总辐射符合余弦分布规律,日最大总辐射照度出现时间通常在每天中午12∶00左右。采用朱伯芳提出太阳总辐射余弦分布模型[12],假设日太阳辐射的峰值时间是中午12∶00,同时作为一天内太阳辐射延续时间的中点值,其数学表达式如下:
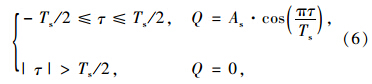
日太阳辐射总量和日照时数两个参数都可以很容易地从气象站获得,参数少,但能够准确模拟正常天气下一天内的太阳辐射情况。
高空大气层和混凝土路面都会发出长波辐射。大气逆辐射和路表长波辐射资料除可从气象站获得外,也可以用Stefan-Boltzmann定律计算得到:
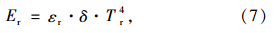
水泥混凝土路面的太阳辐射吸收率取决于表面颜色深度和路表状况,通常范围是0.5~0.6之间。 2.1.3 热交换模型 2.1.3.1 热对流
对流是由于温差所导致的热运动,对流换热是发生在路面板与相接触的大气之间的热量交换。对于路面板这样的水平板,路表上方的风速大小决定了这种对流属于强迫对流还是自由对流。在自由对流的情况下,热量的传输是温度梯度的一个函数。对流换热模型可用式(8)表示:
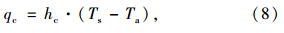
对于水平路面板的对流换热系数,本文采用HIPERPAV II中推荐的公式[13]:
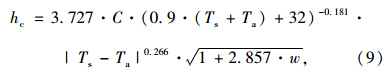
热传导的定义是直接相接触的两种物体之间的热传输。在道路结构中,热传导发生在面层与基层、基层与土层之间。含水率、密度、温度等因素都可以显著影响混凝土的热传导参数。尤其在混凝土硬化过程中,导热系数和比热容受水化进程和温度波动影响,变化较大,不能按照固定常数考虑。
大量研究者测定过混凝土的导热率。可以确定的结论是,硬化初期的导热系数比硬化后混凝土的导热系数高出20%~33%。假设导热系数随着时间的对数是线性下降的,这对于普通水泥非常类似于随水化度增长线性下降,考虑初始值和最终值的关系,可以表示为式(10)[9]:

对于硬化过程中的混凝土,比热容近似是时间对数的线性函数。对于普通水泥,比热容随着水化度的增大而线性下降。本文采用了公式(11)模拟硬化混凝土的比热容变化[9],该模型合理考虑了温度和配合比的影响作用,也体现了随着混凝土硬化,水化度提高对比热容的降低作用。
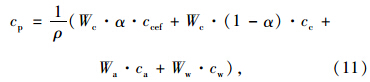
水的蒸发吸热会减小板顶面温度,进而减小路面板内早期的温度梯度。混凝土表面水分蒸发散失热量计算公式为:

式(12)中的混凝土表面水分蒸发速率不容易直接测得。有研究者通过试验得出混凝土表面水分的蒸发速率与自由水面水分蒸发速率之间的关系,指出随着混凝土龄期的增加,两者的比值按指数函数变化。据此,可以根据直接测定的自由水面水分蒸发速率换算得到混凝土表面水分蒸发速率。 2.2 有限差分方程与程序编制
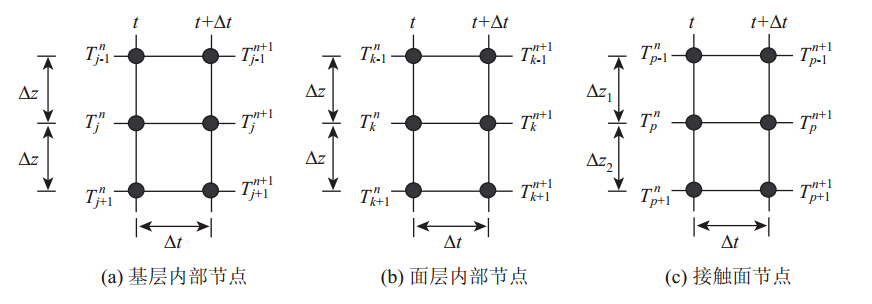
有限差分方法是一种数值方法,可用来解决瞬态传热问题。根据温度场模拟的道路结构材料和热交换物理类型,将有限差分计算的节点类型分为5类:基层内部节点、面层内部节点、表面节点、接触面节点和绝热底部节点。图 3给出了典型节点示意图。
|
| 图 3 典型节点示意图Fig. 3 Schematic diagram of typical nodes |
一维的热传导模型的基本方程可写成式(13):
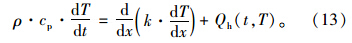
对于基层内部节点,属于无内热源类型,Qh=0,且导热系数k是常数,其节点间的二层差分格式为:
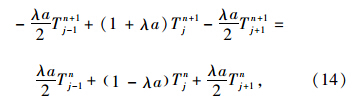
对于路面板内部节点,属于有内热源类型,Qh为水化热。混凝土的比热容和导热系数在硬化过程中不是常数,在上一节热交换模型中假设两者都是水化度的函数,其节点间的二层差分格式为:
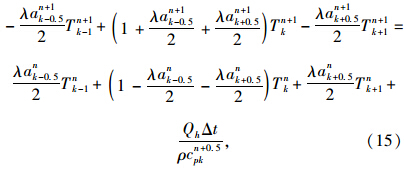
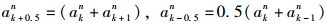 。
。对于表面节点,考虑气温、辐射和热对流等模型,以热流量瞬时平衡作为边界条件;对于路面板与基层、基层与土地基的接触面节点,满足层间接触点温度相等、上下层热流量连续的条件;对于底部节点,一定深度以下土基层在很长一段时间内外部环境对其温度波动影响很小,可以按照绝热条件考虑,即底部热流量为0。
基于以上分析,本文采用Crank-Nicolson格式建立第n时间层和n+1时间相邻3个节点j-1,j,j+1之间的温度数值关系式。这种隐式的二层差分格式是无条件稳定的,其最大的优点是不受显式差分格式中空间步长和时间步长之间的相互制约关系影响,从而可以一次计算较大的时间步长,同时将空间网格划分更细。因为该格式属于加权隐式格式,还需要预估-校正方法来最终完成一个时间步长内的计算。 2.3 参数选取
本文数值模拟程序输入参数列于表 1~表 3,包括:水泥化学组分、水泥细度、水泥用量、水灰比、矿物掺和料用量等水化模型参数,大气温度、风速、相对湿度、太阳辐射、云层状况等气象参数,路面结构和材料、路基初始温度、养护方式和路表状况等热交换参数。
| 路面 结构 | 厚度/ cm | 导热系数/ [(W/m)·℃-1] | 比热容/ [J·(kg·℃)-1] | 密度/ (kg·m-2) | 初始温度/ ℃ |
| 混凝土 路面板 | 16 | 2.52 (硬化后) | 1 021 (硬化后) | 2 400 | 22.0 |
| 贫混凝 土基层 | 20 | 3.32 | 1 005 | 2 340 | 17.8 |
| 土基层 | 200 | 1.51 | 1 000 | 1 780 | 15.0 |
| 材料 | 水泥 | 砂 | 石子 | 水 |
| 用量/(kg·m3) | 380 | 588 | 1 310 | 147 |
| 配合比 | 1.000 | 1.547 | 3.447 | 0.387 |
| 水灰比 | 0.387 | |||
| 名称 | C3S/ % |
C2S % | C3A/ % | C4AF/ % | SO3/ % | 比表面积/ (m2·kg-1) |
活化能/ (J·mol-1) |
| 数值 | 55.7 | 19.1 | 7.7 | 9.1 | 2.1 | 355 | 43 596.9 |
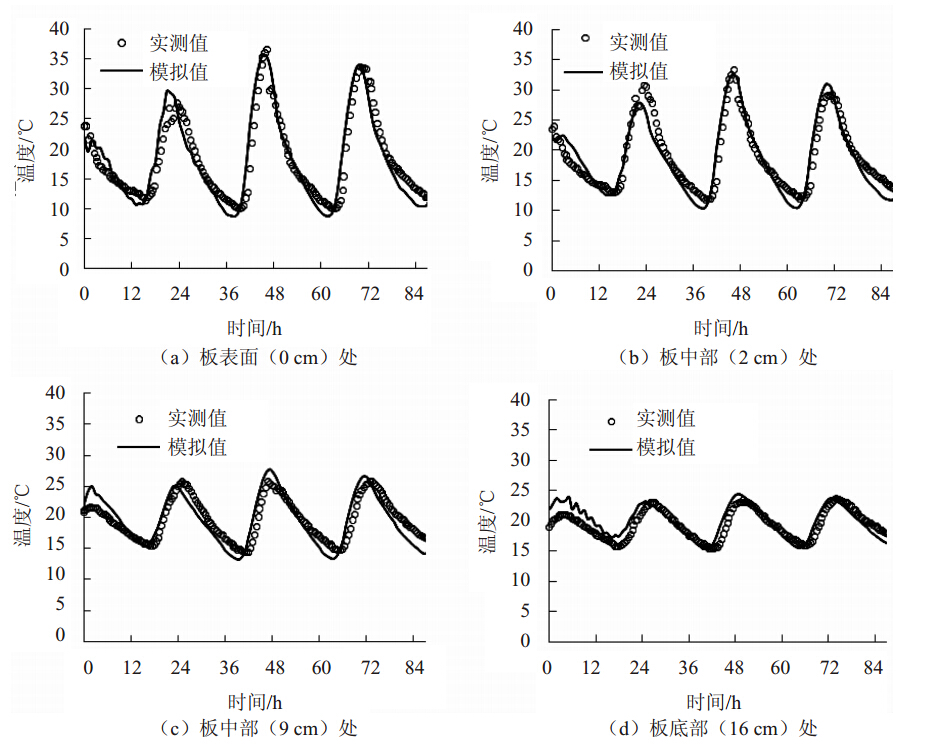
本文编制的Matlab模拟程序采用2.2节列出的5类节点的差分格式,输入2.3节列出的道路材料热物理参数、水泥材料化学参数和气象数据等参数,模拟结果如图 4所示。验证结果表明,本文所建立的一维热传导模拟程序可以较准确地反映水泥混凝土路面板在硬化过程中的温度发展情况。比较不同深度处的实测值与模拟值,可以看出模拟误差一般在2 ℃之内。较大的误差出现在混凝土浇注后前 12 h 内,尤其是靠近板底的部位达到了3 ℃,其原因主要来源于两个方面:一是新拌混凝土温度和路基初始温度的预估误差,尤其是路基初始温度的预测是依据浇注前几天内的天气状况来计算确定;二是前几个小时发生水分蒸发吸热,其与泌水、养护条件等有关,现场因素复杂。因为铺筑时间在下午3点,硬化过程中水化放热的峰值时间处于夜晚,且由于路表面水分蒸发吸热效果,前36 h并没有因为水化放热而造成较大的板内温升,这些都能用本文程序较好地模拟出来。
|
| 图 4 板内不同深度处温度实测值与模拟值 Fig. 4 Measured and simulated temperatures in different depths of slab |
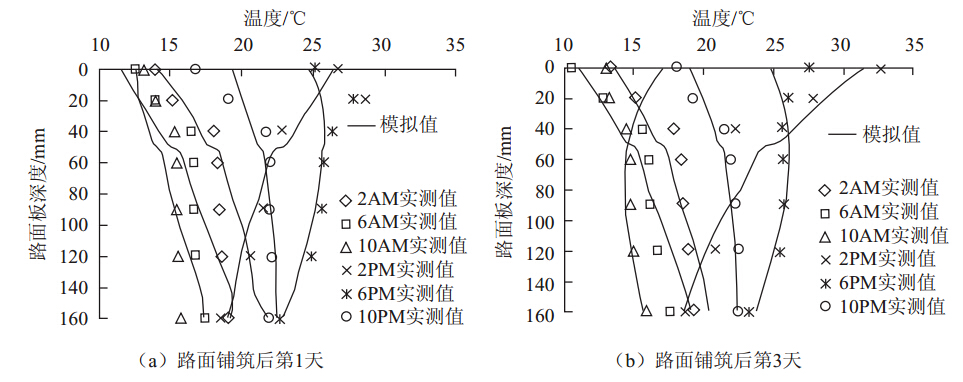
一天内温度沿深度分布如图 5所示:(1)板顶与板底的温度都是先升高后回落,且板顶变化的幅度大于板底,一天内最大可以达到25 ℃。(2)在白天大部分时间里板顶的温度要高于板底,结合图 1(c)可以看出,这一时间段为上午10∶30到晚上19∶00;在夜晚则板底的温度要高于板顶。因此,正温度梯度的时段处于白天,负温度梯度的时间处于晚上19∶00至上午10∶30。从数值上来看,负温差下的温度梯度值比正温差下的温度梯度值小。(3)随着深度的增加,温度梯度不断减小,较大的温度梯度只出现在板内深度40 mm以上部位。在40 mm以下的深度,温度梯度数值较小,温度分布可以近似为线性。
|
| 图 5 一天内温度沿深度分布实测值与模拟值Fig. 5 Measured and simulated temperature distribution along depth in one day |
本研究针对水泥混凝土路面板在硬化过程中的温度分布实测和数值模拟,结论如下:
(1)水泥混凝土路面板内温度呈非线性分布,硬化过程中的水化放热可能会引起较大温升。本试验路面板硬化过程中水化放热的峰值时间处于夜晚,且由于板厚相对较小以及路表面水分蒸发吸热效果,前24 h内并没有因为水化放热而造成较大的板内温升。
(2)路面板内的温度随大气温度和太阳辐射的昼夜变化呈现周期变化,白天路面板内温度的升高主要是由较高的太阳辐射引起,夜晚板内温度的降低则是由大气环境温度下降引起。随板内深度的增加,温度波动的振幅逐渐减小。由实测结果可以看出,随着深度的增加,温度梯度不断减小,较大的温度梯度只出现在板内深度40 mm以上部位,而在40 mm以下的深度,温度梯度值较小,温度分布近似线性。
(3)本文程序模拟结果与实测结果对比表明,模拟结果较为准确,能够反映各实际因素对于路面板内温度变化的影响作用。编制的Matlab数值模拟程序可以为水泥混凝土路面温度场及温度应力的进一步研究提供可靠依据。
| [1] | KUO C M. Effective Temperature Differential in Concrete Pavements [J]. |
| [2] | SCHINDLER A K, DOSSEY T, MCCULLOUGH B F. Temperature Control during Construction to Improve the Long Term Performance of Portland Cement Concrete Pavements [R]. Austin: The University of Texas at Austin, 2002. |
| [3] | BARBER E S. Calculation of Maximum Pavement Temperatures from Weather Reports [J]. Highway Research Board Bulletin, 1957 (168):1-8. |
| [4] | HERMANSSON . Simulation Model for Calculating Pavement Temperatures Including Maximum Temperature [J]. |
| [5] | KELLEY E F. Application of the Results of Research to the Structural Design of Concrete Pavements [J] .ACI Journal Proceedings, 1939, 35(6): 437-464. |
| [6] | 张君, 祁锟, 侯东伟. 基于绝热温升试验的早龄期混凝土温度场的计算[J]. 工程力学, 2009(2): 155-160. ZHANG Jun, QI Kun, HOU Dong-wei. Calculation of Temperature Fields in Early Age Concrete Based on Adiabatic Test [J]. Engineering Mechanics, 2009(2):155-160. |
| [7] | 胡昌斌, 金王杰, 孙增华.水泥混凝土路面早龄期温度场数值模拟研究 [J].工程力学, 2013 ,30(4):175-183. HU Chang-bin, JIN Wang-jie, SUN Zeng-hua. Numerical Simulation of Early-age Temperature of Cement Concrete Pavement[J].Engineering Mechanics, 2013, 30(4):175-183. |
| [8] | BANZANT Z P. Constructive Equation for Concrete Creep and Shrinkage Based on Thermodynamics of Multi-Phase System [C]// Materials and Structures. Paris: RILEM, 1970: 3-36. |
| [9] | SCHINDLER A K, FOLLIARD K J. Heat of Hydration Models for Cementitious Materials [J]. ACI Materials Journal, 2005, 102(1): 24-33. |
| [10] | XU Q, RUIZ J M, HU J, et al. Modeling Hydration Properties and Temperature Developments of Early-Age Concrete Pavement Using Calorimetry Tests [J]. Thermochimica Acta, 2011, 512(1): 76-85. |
| [11] | 严作人. 层状路面体系的温度场分析 [J]. 同济大学学报 :自然科学版, 1984(3): 76-84. YAN Zuo-ren. Analysis of Temperature Field in Layered Pavement System [J]. Journal of Tongji University: Natural Science Edition, 1984(3): 76-84. |
| [12] | 朱伯芳. 大体积混凝土温度应力与温度控制 [M].2版. 北京:中国电力出版社, 1999. ZHU Bo-fang. Thermal Stresses and Temperature Control of Mass Concrete [M]. 2nd ed. Beijing: China Electric Power Press, 1999. |
| [13] | RUIZ J M, RASMUSSEN R O, CHANG G K, et al. Computer-Based Guidelines for Concrete Pavements, Volume III: Technical Appendices [R]. Washington, D.C.: U.S. Department of Transportation, 2006. |
 2015, Vol. 31
2015, Vol. 31

 ,
,