扩展功能
文章信息
- 卢顺达, 程琳
- LU Shun-da, CHENG Lin
- 非对称相位相序方式下的双向绿波协调控制图解法的优化
- Optimization of Bidirectional Green Wave Coordinated Control Graphical Method under Asymmetric Phase Sequence Mode
- 公路交通科技, 2015, Vol. 31 (1): 128-132
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 128-132
- 10.3969/j.issn.1002-0268.2015.01.021
-
文章历史
- 收稿日期:2013-12-03
由于密集的土地开发,在城市道路网络中,相邻交叉口之间的距离通常较近,交通量通常也较大。当采用交通信号灯控制的相邻交叉口距离较短时,就非常有必要协调相邻交叉口交通信号灯的绿灯启亮时间和信号配时方案,使车辆高效率地通过相邻的两个或多个交叉口,这种交通控制方法称为干道信号协调控制,也称绿波协调控制。
双向绿波协调控制比较实用的方法有:数解法[1,2]和图解法[1]。数解法是通过寻找最合适的理想信号位置,需找出各理想信号间距的交叉口挪移量之差最大的理想信号间距,从而确定最合适的理想信号位置,再求得其他参数的一种方法。图解法是通过协调控制的时间-距离图(也称时距图),将信号灯灯色的显示作为时间函数而绘制的两个及两个以上信号灯的协调控制图。时间-距离图按照一定的比例显示交叉口之间的距离,可以直观地将车辆的空间位置表达为关于时间的函数曲线。此外,还有Purdy法、Maxband法以及Multiband法[3,4,5,6,7,8]等。卢凯[9,10] 提出了双向绿波设计方法主要针对不对称的交叉口或交通量,采用交叉口各进口单独放行的方法,在延误和停车次数的减少上取得了良好的效果;马楠等[11,12]提出了基于双向绿波带宽最大化的模型,通过模型计算的方法,实现了双向绿波带宽的最大化。然而,上述方法主要适用进口道对称放行的交叉口群,或是方法过于复杂,可操作性不强,且研究主要针对数解法和建模的方法,对图解法研究甚少,但图解法有简单直观,方便应用的优点,有利于工程应用。本文将采用图解的方法,通过调整交叉口信号相位相序和相位差来优化双向绿波带宽,使主路机动车流能够更顺畅地通过交叉口,并用算例说明方案的有效性。 1 优化方法 1.1 相位相序对配时的影响
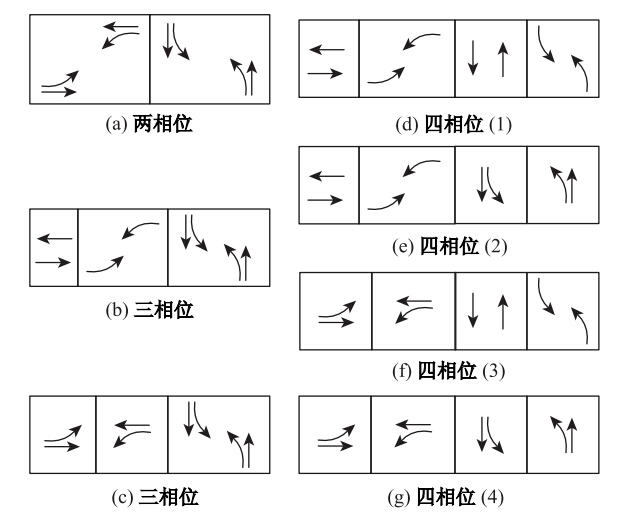
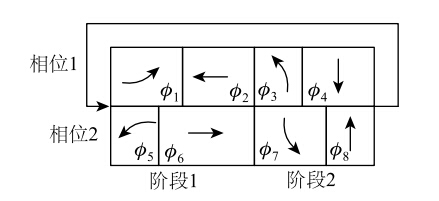
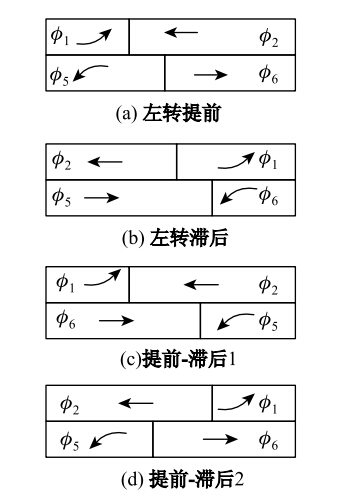
对于普通的十字交叉口,国内一般采用单环结构相位相序方案,如图 1所示,有两相位、三相位、四相位这3种方案。单环结构相位方案采用对称放行的方式,适用于对向交通量相当的交叉口。但在实际道路网络中,交流流量通常表现出不对称性,造成某一方向的绿灯时间不足或另一方向的绿灯时间过剩的情况,使交叉口车辆的运行效率降低。针对上述情况,提出了NEMA相位[13]。与单环结构相位不同的是,NEMA相位是一种双环结构相位,如图 2所示。NEMA相位能根据各进口交通量情况提供多种相位相序选择,如图 3所示,有左转提前、左转滞后和提前-滞后3种方案,其中提前-滞后方案又可细分为主向左转提前及次向左转提前2种方案。[11,12]
|
| 图 1 单环结构相位相序方案示意图Fig. 1 Schematic diagram of single ring phase and phase sequence scheme |
|
| 图 2 双环结构NEMA相位示意图Fig. 2 Schematic diagram of dual ring NEMA phase |
|
| 图 3 NEMA双环结构中4种相位相序方案示意图Fig. 3 Schematic diagram of 4 schemes of phase and phase sequence in NEMA dual ring structure |
由上述可知,NEMA相位能根据交叉口各进口交通量情况提供多种相位方案选择,在进行绿波设计的时候能更灵活地调整配时方案来实现绿波带宽的最大化。 1.2 适用条件
NEMA相位主要适用于非对称交通流的信号交叉口配时。非对称交通流是指在同一相位相对流向交通量差值较大,并满足既定条件的交通流。以十字交叉口东西方向左转交通为例,假设西进口道左转交通量为qwl,东进口道左转交通量为qel,且qwl>qel,交通量相对差值a和饱和度b可表示为:
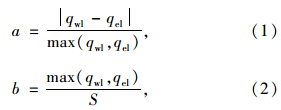
使用经典的图解法求得双向绿波通过带后,可以采用下述方法对绿波带进行优化。
在进行双向绿波设计的时候,制约每个方向绿波带宽的瓶颈交叉口通常情况下是不同的[14],为了获得尽可能大的绿波带宽,可以考虑适当调整瓶颈交叉口相位相序和相位差,使用NEMA相位来改变交叉口车流的放行顺序(不改变原有绿信比),在确保某一方向绿波带宽不降低的前提下,使另一方向的绿波带宽有所增大,甚至是双向的通过带都得到增加。相位差的合理调整,能进一步增大绿波带宽。具体步骤如下:
步骤1 找出制约双向通过带带宽的瓶颈交叉口(详见下例)。
步骤2 使用NEMA相位适当调整瓶颈交叉口相位相序。
步骤3 适当调整瓶颈交叉口的相位差。
步骤4 历遍各瓶颈交叉口,重复步骤1至3,求得系统最优的最大绿波。 3 实例分析
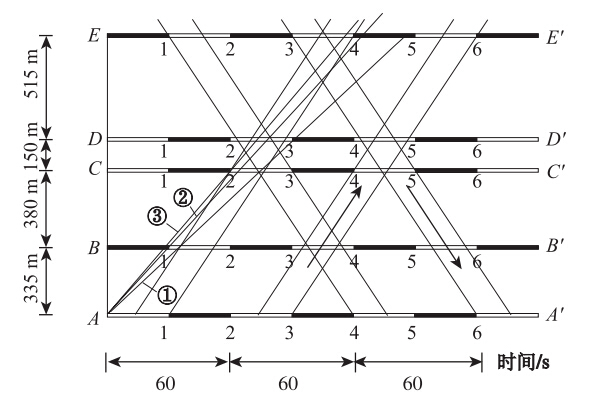
在时间-距离图上用传统的图解法设计双向绿波。如图 4所示,以成都市人民北路一环路段至新华大道段相邻5个十字交叉口(北至南依次编号:A,B,C,D,E),作为一个绿波协调控制系统,绿波带速设为35 km/h左右,公共周期预设为60 s。图 4中黑线段表示红灯时段,如A交叉口横线AA′上的1-2,3-4,5-6段;空白段表示绿灯时段,如横线AA′上的A-1,2-3,4-5,6-A′段。
|
| 图 4 图解法示例Fig. 4 An example of graphical method |
(1)由A点引一条绿波带速度为35 km/h的斜线①,自AA′上的1点引出的垂直线同BB′线的交点(BB′线上的1点)和斜线①与线BB′的交点非常靠近。A,B交叉口的绿时差可通过BB′上的1点确定,因此交叉口A,B采用交互式协调控制方式;在BB′线和AA′线上画出红灯和绿灯时长线段,如图 4所示。
(2)从A点引一直线至BB′上的1点成斜线②,自AA′上2点引出的垂直线与CC′的交点(CC′上的2点)和斜线②在CC′的交点非常靠近,B,C交叉口的绿时差可通过CC′上的2点确定,因此交叉口B,C采用交互式协调控制方式;在CC′线上画出红灯和绿灯时长线段,如图 4所示。
(3)从A点引一直线至CC′上的2点成斜线③,自AA′上2点引出的垂直线与DD′的交点(DD′上的2点)和斜线③在DD′的交点非常靠近,因此交叉口C,D采用同步式协调控制方式;在DD′线上画出红灯和绿灯时长线段,如图 4所示。
(4)同理,用上述方法做出线EE′上的红灯时长,并确定协调控制方式。这样由5个交叉口组成的双向绿波协调控制系统初步设计完成。
(5)在图 4中画出绿波带,经计算得到,绿波带宽度为16 s,占公共周期60 s的27%,绿波带速度为56 km/h。这样的绿波带速度相比于城市中的平均车速相比明显偏高,因此必须降低绿波带速度,可考虑将绿波带速度设置在40 km/h上下,将公共周期时长增大至85~90 s即可实现。
(6)最后,需调整各交叉口的绿信比,但由于各交叉口绿信比各不一样,可将按以上步骤确定的各交叉口红灯(或绿灯)的中心点固定住,根据需要调整到的实际时长增大或缩小即可[15]。
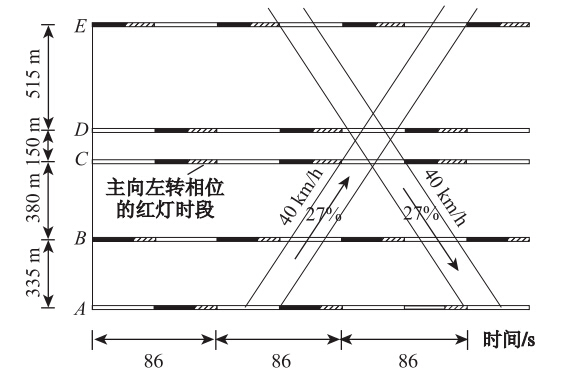
假设由上述5个交叉口组成的某干道系统的配时方案如表 1所示。周期时长取86 s,相位顺序为主向左转,主向直行,次向直左。此时绿波带速度为40 km/h,如图 5所示,图中斜线表示主向左转相位的红灯时段。
| 交叉口ID | 交叉口类型 | 相对交叉口间距/m | 主向直行/s | 主向左转/s | 次向直左/s |
| A | 十字 | 0 | 43 | 15 | 28 |
| B | 十字 | 335 | 43 | 15 | 28 |
| C | 十字 | 380 | 43 | 20 | 23 |
| D | 十字 | 150 | 43 | 20 | 23 |
| E | 十字 | 515 | 43 | 20 | 23 |
|
| 图 5 双向绿波设计Fig. 5 Design of bidirectional green wave |
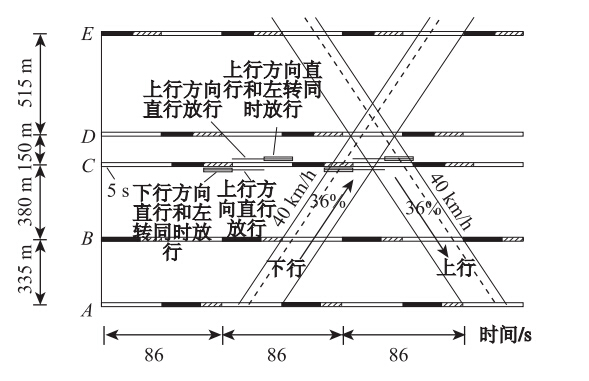
如图 5所示,C交叉口的绿灯时间已经充分利用,若要使绿波带加宽,必须改变C交叉口的相位相序(在不改变绿信比的前提下),将C交叉口定为瓶颈交叉口。对原本对称放行的干道绿波控制系统进行优化,通过改变相位相序的方法,将C交叉口的相位相序改成图 3(c)所示的主向左转提前-滞后的模式。与此同时,适当调整C交叉口的相位差(调整幅度为5 s,如图 6所示),使其满足绿波带加宽的要求。调整后的双向绿波设计如图 6所示。
|
| 图 6 优化后的双向绿波设计Fig. 6 Optimized design of bidirectional green wave |
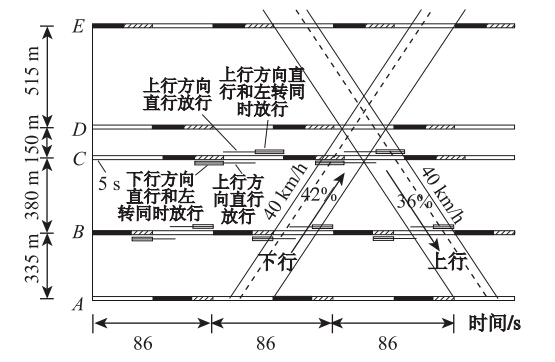
历遍所有交叉口,得到最终的优化方案如图 7所示。
|
| 图 7 最终优化的双向绿波设计Fig. 7 Final optimized design of bidirectional green wave |
通过调整瓶颈交叉口的相位相序和相位差,可得到优化的双向绿波协调控制效果,绿波带宽效率由原来的下行27%,上行27%,增加到下行42%,上行36%,绿波协调控制效果得到了有效提升,分别提升了56%和33%,可有效减小整个系统的车辆平均延误、平均停车次数。 4 结论
综上所述,与对称放行方式下的传统绿波图解法相比,采用改进后的图解法,能使双向绿波带宽效率得到有效地提高,使车辆能够更通畅地通过各个交叉口,到达协调控制的效果,且图解法简单直观,便于工程应用。此方法也适用于数解法的优化,用数解法求得双向绿波后,可绘制时距图,通过调整瓶颈交叉口的相位相序和相位差对绿波带进行优化。但随着交叉口交通流量的增加,需要对交叉口的信号配时、相位相序、相位差进行重新调整和优化来确保绿波的可行性。
| [1] | 中国公路学会.交通工程手册[M].北京:人民交通出版社,1998. China Highway Association. Traffic Engineering Manual[M].Beijing: China Communications Press,1998. |
| [2] | 卢凯,徐建闽,叶瑞敏.经典干道协调控制信号配时数解算法的改进[J].公路交通科技,2009,26(1):120-124,129. LU Kai,XU Jian-min,YE Rui-min. Improvement of Classical Algebraic Method of Signal Timing for Arterial Road Coordinate Control[J].Journal of Highway and Transportation Research and Development,2009,26(1):120-124,129. |
| [3] | GARTNER N H,ASSMAN S F,LASAGA F,et al. A Multi-band Approach to Arterial Traffic Signal Optimization[J]. Transportation Research Part B: Methodological,1991,25(1):55-74. |
| [4] | LITTLE J D C. The Synchronization of Traffic Signals by Mixed-integer Linear Programming[J].Operations Research,1966,14(4):568-594. |
| [5] | MORGAN J T,LITTLE J D C. Synchronizing Traffic Signals for Maximal Bandwidth[J].Operations Research,1964,12(6):896-912. |
| [6] | TIAN Z,MANGAL V,LIU H. Effectiveness of Lead-lag Phasing on Progression Bandwidth[J]. Transportation Research Record,2008,2080:22-27. |
| [7] | MESSER C J,WHITSON R N,DUDEK C L,et al. A Variable-sequence Multiphase Progression Optimization Program[J].Highway Research Record,1973(445): 24-33. |
| [8] | 沈国江,许卫明.交通干线动态双向绿波带控制技术研究[J].浙江大学学报:工学版,2008,42(9): 1625-1630. SHEN Guo-jiang,XU Wei-ming. Study on Traffic Trunk Dynamic Two-direction Green Wave Control Technique[J]. Journal of Zhejiang University: Engineering Science Edition,2008,42(9):1625-1630. |
| [9] | 林晓辉,徐建闽,卢凯,等.各进口单独放行条件下的双向绿波设计方法研究[J].交通与计算机,2007,25(5):8-12. LIN Xiao-hui,XU Jian-min,LU Kai,et al. A Design Method of Two Way Green Wave of Each Phase for Entrance [J]. Computer and Communications,2007,25(5):8-12. |
| [10] | 卢凯,徐建闽,李轶舜.进口单独放行方式下的干道双向绿波协调控制数解算法[J].中国公路学报,2010,23(3):95–101. LU Kai,XU Jian-min,LI Yi-shun. Algebraic Method of Arterial Road Coordinate Control for Bidirectional Green Wave Under Signal Design Mode of One-phase-one-approach[J]. China Journal of Highway and Transport,2010,23(3):95-101. |
| [11] | 马楠,邵春福,赵熠.基于双向绿波带宽最大化的交叉口信号协调控制优化研究[J].吉林大学学报:工学版,2009,39(增2):19-24. MA Nan,SHAO Chun-fu,ZHAO Yi. Optimized Modeling of Signalized Intersections Coordination Based on Two-way Bandwidth Maximization[J].Journal of Jilin University: Engineering and Technology Edition,2009,39(S2):19-24. |
| [12] | 马楠,邵春福,赵熠.干道信号交叉口群协调控制系统中的影响因素[J].哈尔滨工业大学学报,2011,43(6):112-117. MA Nan,SHAO Chun-fu,ZHAO Yi. Influence Factors of Coordination Control System in Signalized Intersections[J]. Journal of Harbin Institute University,2011,43(6):112-117. |
| [13] | PROTHMANN H,BRANKE J,SCHMECK H,et al. Organic Traffic Light Control for Urban Road Networks[J]. International Journal of Autonomous and Adaptive Communications Systems,2009,2(3): 203-225. |
| [14] | 卢凯,徐建闽,陈思溢,等.通用干道双向绿波协调控制模型及其优化求解[J].控制理论与应用,2011,28(4):551-555. LU Kai,XU Jian-min,CHEN Si-yi,et al. A General Model of Bidirectional Green Wave for Coordinate Control of Arterial Road and Its Optimization Solution[J].Control Theory & Applications,2011,28(4):551-555. |
| [15] | 沈大吉. 基于交通冲突安全评价的城市干线交叉口信号协调控制研究[D]. 重庆:重庆交通大学,2010. SHEN Da-ji. Coordination Control of Urban Trunk Intersection Signal Based on Safety Evaluation of Traffic Conflict[D]. Chongqing: Chongqing Jiaotong University,2010. |
 2015, Vol. 31
2015, Vol. 31
