扩展功能
文章信息
- 曲大义, 陈文娇, 郭涛, 杨万三, 王兹林
- QU Da-yi, CHEN Wen-jiao, GUO Tao, YANG Wan-san, WANG Zi-lin
- 考虑横向干扰的交叉跟驰模型研究
- Research on Staggered Car-following Model Considering Lateral Disturbance
- 公路交通科技, 2015, Vol. 31 (1): 122-127
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 122-127
- 10.3969/j.issn.1002-0268.2015.01.020
-
文章历史
- 收稿日期:2014-05-05
车辆行驶在车道中间受前车的影响且不允许超车是跟驰理论的重要前提[1]。如果每辆车都是按规定行驶在道路的中心线上,则相邻车道的车辆对目标车的影响可以忽略。但经调查研究发现,由于受驾驶技术、车道宽度和路面条件等因素的影响,并非每辆车都行驶在车道的中心线上,因此会对相邻车道的行驶车辆产生一定的干扰作用,在车队中呈现车辆交叉跟驰现象。而这种干扰在研究车辆跟驰行为时是不可忽略的。
自从Reusehel[2]和Pipes[3]利用运筹学技术首次成功解析跟驰模型以来,几十年间国内外众多研究人员根据交通流的本质特征,对跟驰模型不断地进行研究,先后出现了很多著名的跟驰模型。Kometani和Sasaki[4]提出了安全距离跟驰模型,模型假设驾驶员在不能完全预判前车运动的情况下,保持合理的安全间距以避免碰撞。Michaels和Evans等人[5,6]提出了驾驶员心理跟驰模型,模型假设驾驶员按照前后车之间的相对运动(包括速度和距离的变化)来调节跟驰速度。 Bando等人[7,8,9]提出了优化速度模型,受到了广泛的重视。与此同时,国内学者蒋磺、王殿海、贾洪飞、贺国光、葛红霞、许伦辉等人都对车辆跟驰行为进行了深入研究[1,10,11,12,13]。但基于单车道跟驰行为的多数研究,基本假设都是车辆沿车道中心线行驶,而对横向干扰及多车道上的跟驰行为研究较少。因此,在研究车辆的跟驰行为时,考虑相邻车道的车辆对跟驰车辆的横向干扰作用是跟驰理论的一个重要延伸。
本文将在国内外对跟驰行为研究的基础上,以跟随车所受的横向干扰为基础,依据安全距离跟驰行为,对传统的跟驰模型进行改进,建立交叉跟驰模型,并对其进行交通仿真和数理统计分析,进一步验证模型的准确性和适用性。 1 车辆横向干扰影响分析
对某地快速路进行实地调查。根据获取的数据分析可知,行驶车辆所处的横向位置基本符合正态分布,车辆行驶在车道线甚至是边缘线的案例屡见不鲜。而车辆偏移车道中心线行驶主要表现为:道路上车辆不规则的横向位置、长时间行驶在车道线上、利用路肩作为车道、侧向间隙受限制时速度被影响等。根据道路上行驶车辆的运行特征,车辆之间的横向间距与跟驰距离的关系主要有以下4种:正常跟驰、交叉跟驰(部分重叠)、交叉跟驰、没有跟驰,如图 1所示。

|
| 图 1 横向间距和跟驰距离关系的趋势图Fig. 1 Trend of relation between lateral spacing and following distance |
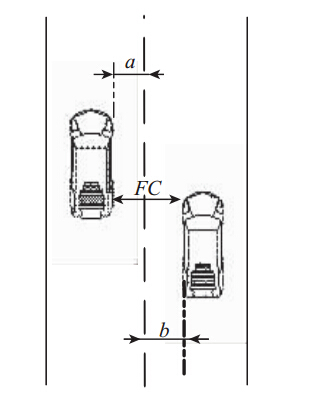
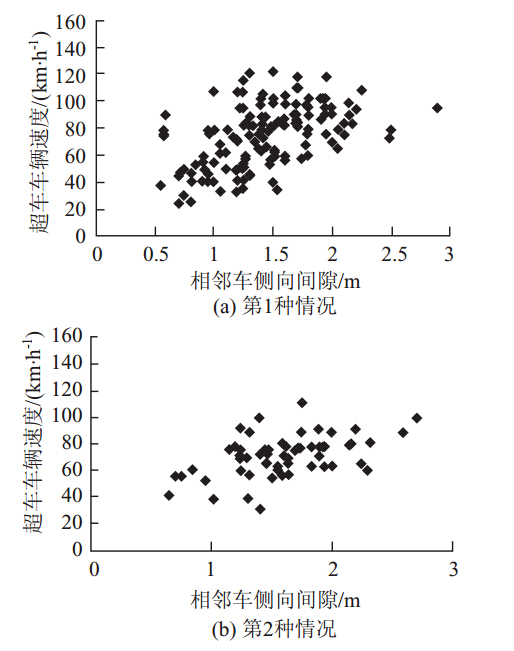
车辆偏离车道的中心线行驶,相邻车辆呈现图 1中的交叉跟驰(部分重叠)和交叉跟驰的现象,宏观表现为不整齐的车流。而此种现象正是车辆之间的横向干扰造成的。此外,若车辆想加速超车,基于横向干扰因素的存在,超车驾驶员需要根据被超车的横向位置进行决策,如图 2所示。因此,在不整齐的车流中,相邻车辆之间的侧向间隙FC在一定程度上会影响到超车速度,随着FC的增大,超车速度变大,如图 3所示。
|
| 图 2 在双车道上相邻车的侧向干扰Fig. 2 Lateral disturbance of adjacent vehicles on a 2-lane road |
|
| 图 3 不同位置上FC与超车速度的关系Fig. 3 Relation between FC and passing speed at different locations |
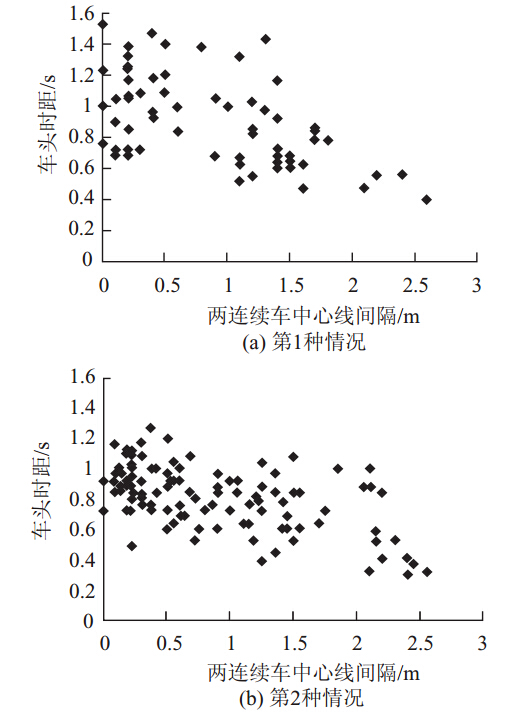
图 4描述了一种交叉跟驰的场景,其中CS是两辆连续车间的中心线间隔。若想探究两辆连续车之间横向间隙和车头时距的关系,则需要做进一步分析。在整齐的车流中,因为CS变化不明显,所以无法阐述。但是从不整齐的车流中可以发现,随着CS的增大(图 5),车头时距变小。这表明当车辆间存在中心分离时,车辆倾向于保持较短的车头时距。

|
| 图 4 典型交叉跟驰示意图Fig. 4 Schematic diagram of a typical staggered car following situation |
|
| 图 5 两辆连续车的车头时距与CS的关系Fig. 5 Time headway vs. CS of 2 consecutive vehicles |
在传统的跟驰模型中,若前导车某时刻突然减速甚至停止,跟随车为避免与前导车发生碰撞,需要及时采取减速措施。这在一定程度上会影响到跟随车的行驶效率。事实上,在交叉跟驰过程中,为避免与前导车发生追尾,跟随车在感知前导车减速时,不需要始终追随前导车,可以考虑把车转向其他可利用空间,以此来规避前导车。此措施与传统跟驰模型不同的是跟随车不需要减速至零,但是跟随车需要在疏散路径内完成操纵。疏散路径即图 1中相邻两车之间的跟驰距离,跟随车需要在跟驰距离范围内完成转向操作,之后在可利用的空间内加速超过前导车或保持转向速度继续行进。在此,用最大转移速度(Maximum Escape Speed,MES)标定跟驰距离,因此,允许的最大转移速度由两个限制性因素决定:一是跟随车可以减速至疏散路径允许的最大速度;二是保证跟随车不与前导车发生碰撞且有足够时间完成转向操纵的速度。
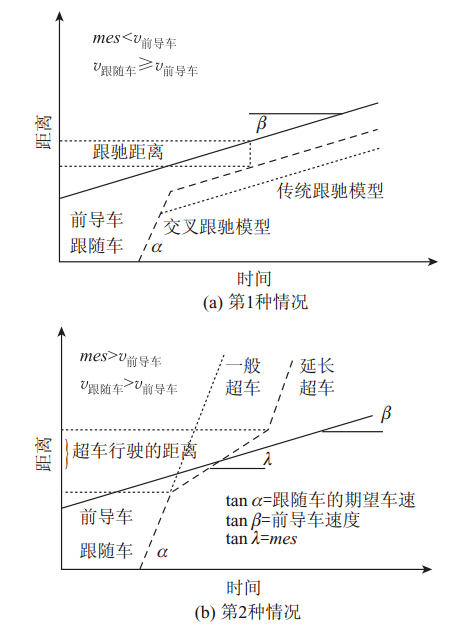
为便于理解,图 6描述了车辆之间相互关系的动力学特性。在图 6 (a)中,最大转移速度小于前导车的速度,因此不满足跟随车超车条件。在给定时间内,跟驰距离小于传统跟驰模型的跟驰距离。在图 6 (b)中,跟随车的速度不必恒定,但须大于前导车的速度,且前导车的速度小于前导车侧向路径宽度允许的MES。跟随车向前导车靠近,当达到两车之间的速度差时,跟随车就会决定超车,但是超车的速度受MES的限制。
|
| 图 6 两种不同情况交叉跟驰的时空图Fig. 6 Space-time diagrams of 2 staggered car following cases |
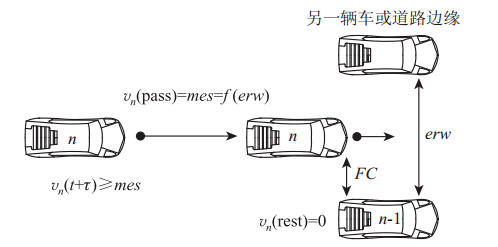
假设在标准车道和肩宽的道路上,车辆两侧有足够的侧向间隙,则驾驶员以设计车速行驶。新的跟驰模型假设车辆速度受行驶路径宽度的影响,即指图 7的有效路径宽度(Effective Route Width,ERW)。图 3已经表明FC较大时,相邻车对正在超车的影响可以忽略。假设车辆两边的FC相同,因为在现实生活中驾驶员倾向于行驶在路径中间。
|
| 注:erw为有效路径宽度。 图 7 FC影响下的车辆跟驰Fig. 7 Car-following under influence of FC |
从动力学角度看,车辆的相互关系可以表示为:
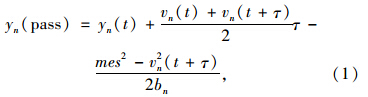
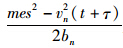 为跟随车在减速过程中行驶的距离;mes为最大转移速度。
为跟随车在减速过程中行驶的距离;mes为最大转移速度。yn-1(rest)为跟随车前导车停下时的纵向位置。为了安全跟驰,yn-1(rest)-sn-1应该大于yn(pass),则:
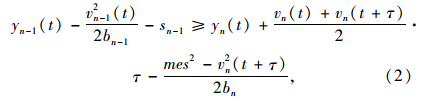
为防止驾驶员操纵失误,设定安全界限{vn(t+τ)}θ,θ在Gipps[15]模型中被赋予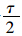 ,则式(2)转化为:
,则式(2)转化为:
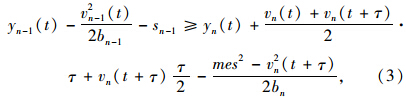
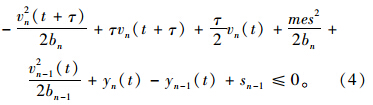
二次不等式(4)是αx2+βx+γ≤0的形式,式中
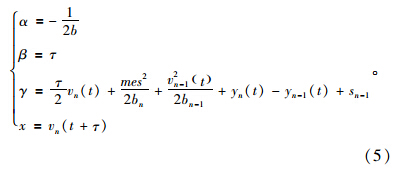
不等式的两个根可以通过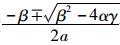 计算求出。这里不需要负速度值,所以跟随车在反应时间末的速度应该为:
计算求出。这里不需要负速度值,所以跟随车在反应时间末的速度应该为:
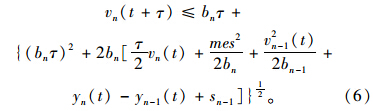
为维持必需的安全距离,这个速度是跟随车在反应时间末不应该超出的最大速度。简而言之,疏散路程越宽,MES值越大,因此随着vn(t+τ)的增大,需要的最小安全跟驰距离越长。需求不等式允许范围内选取的具体值用在仿真模型中,可以简单地假定它为一个等式。当MES值为0时,式(6)的结果与Gipps[14]模型一致。
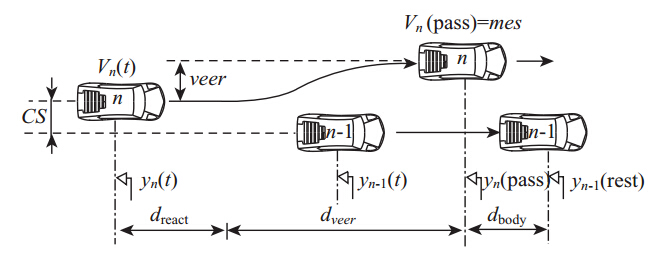
如图 8所示,当侧向偏移较明显时,需要做进一步的分析,此时的换道只是部分性,即完成一个必需的横向偏移而不是基于车道变换。那是车辆转向避免碰撞所需的时间,即使疏散路程足够宽。这个距离不是额外增加到式(6)计算出的跟驰距离上,为简单起见,假设跟随车可以完成减速并同时产生横向偏移。
|
| 图 8 交叉跟驰中车辆紧急制动下跟随车运动变化示意图Fig. 8 Movement of following car under emergency braking in staggered car-following |
对于前导车旁边的一条安全通道来说,跟驰应满足以下条件:
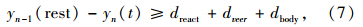
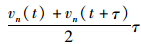 ;dveer为跟随车转向操作期间可能存在的减速行驶距离,
;dveer为跟随车转向操作期间可能存在的减速行驶距离,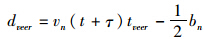 ·(tveer)2,tveer是以防前导车突然制动跟随车完成必要的横向偏移所需的时间;dbody为跟随车完成横向偏移时与前导车的距离。
·(tveer)2,tveer是以防前导车突然制动跟随车完成必要的横向偏移所需的时间;dbody为跟随车完成横向偏移时与前导车的距离。
为方便起见,将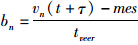 改写成bn=-
改写成bn=-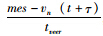 ,式中,
,式中,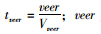 ;veer为横向偏移量;Vveer为最大的横向偏移速度。则式(7)可以转化为:
;veer为横向偏移量;Vveer为最大的横向偏移速度。则式(7)可以转化为:
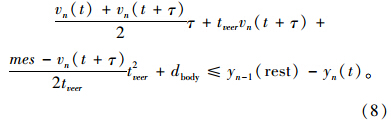
将式(8)化简得:
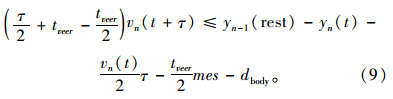
为了完成必需的转向操纵,跟随车在反应时间末的速度不应该超过式(10)。换言之,veer的值越大,安全跟驰距离越长。
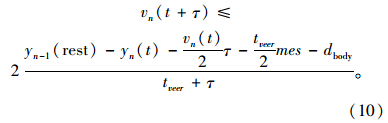
简言之,式(6)或式(10)构造了跟驰模型的新形式,在此限定条件下求解车辆的最大转移速度。 3 仿真分析 3.1 仿真原理
将最大转移速度作为FC的一个函数进行计算。当FC<0.5 m,则mes=0,因为此时无法实现超车,这与传统跟驰相吻合;若0.5 m<FC<1.5 m,根据图 3的数据,给定FC,选取相应的速度进行拟合,得到一条二阶曲线:
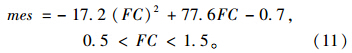
当FC>1.5 m时,邻车的影响微乎其微,在此假设可以忽略,此时MES值与跟随车速度相同,即跟随车运动不受任何交叉前导车的限制。
由式(6)得知,前导车的速度和MES起限定作用,通过计算vn(t+τ),得出计算跟随车在反应时间末的纵向位置的动力学关系式:
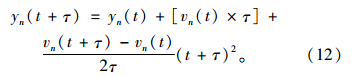
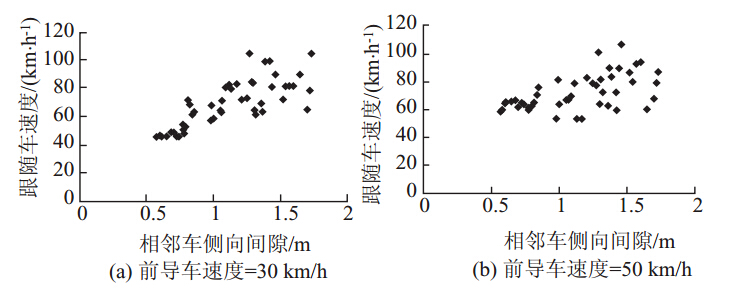
取FC=(erw-跟随车的宽度)/2。为了较为明显地观察FC对跟随车速度的影响,将前导车的速度限定在30~50 km/h范围内,如图 9所示。由此发现随着跟随车行驶路径宽度的增大,跟随车的速度也增大。当FC小于0.5 m时,二者之间没有关系,表明此阶段跟随车不会选择超车,而是跟随前导车。当FC大于1.5 m时,跟随车受到的影响也不明显。
|
| 图 9 FC和跟随车速度的仿真关系Fig. 9 Simulated relation between FC and passing speed |
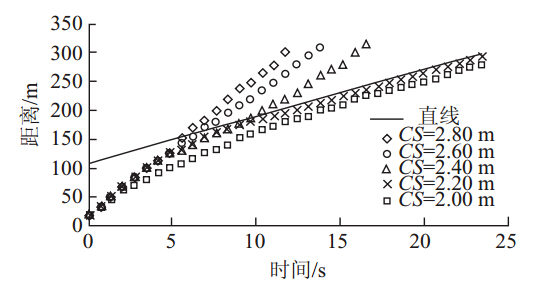
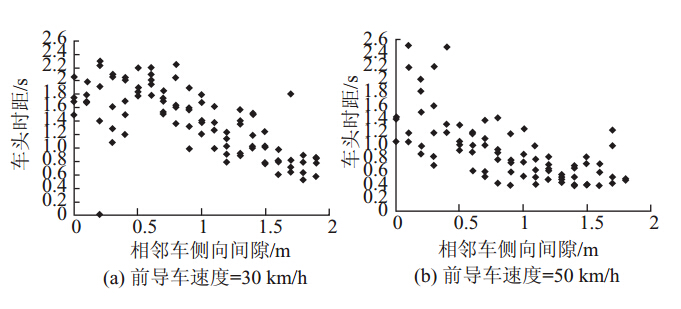
当跟随车前面只有1辆前导车,且跟随车不在道路的边缘行驶,那么就不会有疏散通道,从而不会有MES值的限定。此时,车辆中心线间隔值是分析跟随车运动的主要因素。假定跟随车初始速度为90 km/h,前导车速度为30 km/h,仿真结果如图 10所示。可以看出,当CS<2 m时,描述的是传统的跟驰过程;当2 m<CS<2.6 m时,则会产生交叉跟驰现象;当CS≥2.8 m时,不存在车辆跟驰行为。图 11揭示出随着CS增大而车头时距呈下降关系。
|
| 图 10 不同CS下车辆跟驰仿真轨迹Fig. 10 Simulated trajectories of a vehicle in different CS values |
|
| 图 11 CS与车头时距的仿真关系Fig. 11 Simulated relation between CS and time headway |
本文在对实际交通场景车辆行驶情况进行分析的基础上,通过引入最大转移速度和疏散路径2个参数,考虑横向干扰对车辆跟驰行为产生的影响,建立了交叉跟驰模型,并以其为限定条件对跟随车的车速进行了调整,以保证车辆的安全跟驰。此外,在前导车不同车速状态下对FC与跟随车速度之间的关系和不同CS下的车辆跟驰轨迹进行了仿真分析,发现FC在0.5~1.5 m的范围内时,跟随车的速度随着FC的增大而增大;当2 m<CS<2.6 m 时,车辆之间存在交叉跟驰行为。仿真结果进一步验证了交叉跟驰模型更能客观地描述车辆的跟驰行为。
| [1] | 王殿海.交通流理论[M].北京:人民交通出版社,2001. WANG Dian-hai. Traffic Flow Theory[M]. Beijing:China Communications Press,2001. |
| [2] | REUSCHEL A. Vehicle Movements in a Platoon[J]. Oesterreichisches Ingenieeur-Archir, 1950, 4:193-215. |
| [3] | PIPES L A. An Operational Analysis of Traffic Dynamics[J]. Journal of Applied Physics,1953, 24(3):274-281. |
| [4] | KOMETANI E, SASAKI T. On the Stability of Traffic Flow, Report No. 1 [R]. Tokyo: Operations Research Society, 1958: 11-26. |
| [5] | MICHAELS R M. Perceptual Factors in Car Following[C]// Proceedings of International Symposium on the Theory of Road Traffic Flow. London: OECD,1963: 44-59. |
| [6] | EVANS L, ROTHERY R. Perceptual Thresholds in Car Following: Comparison of Recent Measurements with Earlier Results[J]. Transportation Science, 1977, 11(1): 60-72. |
| [7] | BANDO M, HASEBE K, NAKANISHI K, et al. Phenomenological Study of Dynamical Model of Traffic Flow[J]. Journal de Physique I France, 1995, 5(11): 1389-1399. |
| [8] | BANDO M, HASEBE K, NAKAYAMA A, et al. Dynamical Model of Traffic Congestion and Numerical Simulation[J]. Physics Review E, 1995, 51(2): 1035-1042. |
| [9] | BANDO M, HASEBE K, NAKANISHI K, et al. Analysis of Optimal Velocity Model with Explicit Delay[J]. Physical Review E,1998, 58(5): 5429-5435. |
| [10] | 陶鹏飞.考虑侧向车影响的跟驰行为分析与建模[D].吉林:吉林大学,2009. TAO Peng-fei. Analysis and Modelling on Car-following Behavior Considering Impact of Lateral Vehicles[D]. Jilin: Jilin University,2009. |
| [11] | 贾洪飞,隽志才,王晓原.基于神经网络的车辆跟驰模型的建立[J].公路交通科技,2001,18(4):92-94. JIA Hong-fei,JUAN Zhi-cai,WANG Xiao-yuan. Development of a Car-following Model Based on Artificial Neural Networks[J]. Journal of Highway and Transportation Research and Development, 2001,18(4):92-94. |
| [12] | 宋现敏,金盛,王殿海,等.考虑侧向偏移的车辆跟驰模型[J].吉林大学学报:工学版,2011,41(2):333-337. SONG Xian-min,JIN Sheng,WANG Dian-hai,et al. Vehicle-following Model Considering Lateral Offset[J]. Journal of Jilin University:Engineering and Technology Edition,2011,41(2):333-337. |
| [13] | 曲大义,杨建,陈秀峰, 等.车辆跟驰的分子动力学特性及其模型[J].吉林大学学报: 工学版,2012,42(5): 1198-1202. QU Da-yi,YANG Jian,CHEN Xiu-feng, et al. Molecular Kinetics Behavior of Car-following and Its Model[J]. Journal of Jilin University: Engineering and Technology Edition,2012,42(5): 1198-1202. |
| [14] | GIPPS P G. A Behavioral Car Following Model for Computer Simulation[J]. Transportation Research Part B: Methodological, 1981,15(2): 105-111. |
 2015, Vol. 31
2015, Vol. 31
