0 引言

道路交叉口作为城市道路网络中的节点，是交通拥挤、交通事故的常发地点,而自适应交通信号控制对于缓解城市交叉口的交通拥挤有很大的潜力^[1]。20世纪70年代，国内外学者采用模糊控制方法、遗传算法、神经网络^[2,3,4,5]等应用在交叉口自适应交通信号控制中，取得了较好的效果，但在一定程度上不能适应多变的交通流特征。Watkins^[6]提出的Q-强化学习方法由于不需要外部环境的数学模型，对环境的先验知识要求低，能够实时地适应交通条件的变化，在自适应交通信号控制中有广阔的发展前景。目前国外一些研究，如文献^[7,8]等将传统的强化学习算法应用到交叉口自适应交通信号控制中，取得了较好的效果，但存在维数灾难问题：算法普遍要求完全状态表示，随着交叉口的增加，状态和动作空间呈指数增长，因此很难直接应用于多交叉口路网。除了维数灾难问题，这些方法需要每个agent观察整个系统的状态，这在较大交通网络情况下是不可行的。虽然目前有学者在强化学习中利用非线性函数估计，但收敛性不一定能得到保证。因此，针对以上不足，通过有效地利用基于特征的状态表示法，将拥挤水平表示为低、中、高3种特征，并采用线性平均函数估计思想，以解决维数灾难和收敛性的问题。此算法的运行只需要特征信息，而不需要一些精确信息如每个车道的排队长度等，所需要的特征数与信号控制的车道数呈线性关系，因此其计算复杂度降低了多个数量级。在设置的多交叉口交通环境下，仿真试验分析表明此算法是有效和收敛的。 1 自适应交通信号控制问题的MDP模型

自适应交通信号控制问题可以利用MDP建模。MDP模型描述见文献^[9]。为每个信号控制的交叉口定义1个agent，对交叉口所有相位的交通流进行控制。下面对交叉口自适应交通信号控制MDP模型中的状态、动作和回报值等进行描述。 1.1 状态定义：排队长队

设s^k为交叉口agent在时间步k的状态，定义见式(1)^[10]：

式中，a^k 为交叉口agent在时间步k的当前绿灯相位号;EGT_a^k为当前相位的运行绿灯时间;L_l为每个相位的车道的集合;q_l^k为在时间步k车道l所排队的车辆数;P为相位数。当某车辆的速度低于某特定速度阈值时，此车辆将被加入队列。q_l^k的计算式为: 式中,V_l^k为在时刻k驶入车道l的车辆集合;Sp_thr为速度阈值。 1.2 动作定义：可变相位序列

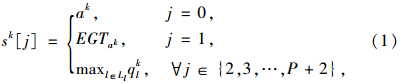
此算法的设计考虑可变的相位序列，其控制行为不再是固定相位序列方法中用到的当前相位的延续或者终止。相反地，此算法根据交通流的波动来延长当前相位或者切换到其他相位，可能跳过不必要的相位。因此，此定义采用具有可变相位序列的非循环配时方案，其周期和相位序列均不是预定的。所以，时间步t的动作a_k定义为下次将生效的相位p：

式中P为所有可能相位的个数。值得注意的是，如果动作与当前绿灯相位相同，此相位的绿灯时间将被延长1个特定的时间间隔(如1 s)，绿灯将被切换到相位ak。时间间隔Δk的定义为: 式中，Gakmin为ak的最小绿灯时间；Yak为ak的黄灯时间；Rak为ak的全红时间。 1.3 回报值定义：总累积延误的减少

由于每个交叉口agent的目标是最小化此交叉口的总的车辆延误，因此回报函数定义为总的累积延误的减少，并且每个交叉口的agent的回报值是不同的。首先，定义时间步k的车辆v的累积延误为Cd_v^k，它表示排队(由某特定速度阈值Sp_thr定义)中的车辆v直到时间步k所花的总的时间。相位p的累积延误是当前行驶在车道集合L_p的所有车辆的累积延误的总和(式(5))：

式中，Δ^k-1为在时间步k的决策点前先前时间步的持续时间；Sp_v^k是车辆在时刻k的速度。

某交叉口agent的即时回报r^k定义为其总的累积延误的减少量(式(6))，即两个连续决策点的总的累积延误的差值。回报值为正表明经过运行所选择的动作后总的累积延误减少，回报值为负表明此动作导致了总的累积延误的增加。

2 基于特征表示的强化学习算法

传统的强化学习算法如Q-学习通过运行增量随机算法来获得最优配置策略，但需要查找表来存储每个可能(s,a)元组的Q值。虽然这种情况在较小的状态和行动空间中是可行的，但由于查找表需要很多存储空间，并且随着(s,a)元组数目的增加，对于每个(s,a) 元组的Q(s,a)的查找和更新操作又产生了额外的计算时间和空间，因此对于涉及到多个交叉口的较大路网来说,计算上的开销是很高的。当交叉口数目增加时，状态和行动空间的大小将呈指数级增长。为了缓解维数灾难的问题，引入线性函数估计及基于特征的方法，值函数利用参数化的拟合函数来代替查找表，参数的维度远小于状态数，通过对计算复杂性进行控制来处理上述问题。 2.1 算法的基本思想

在基于特征表示的强化学习环境下，其思想是根据线性梯度下降法估计动作-状态值函数(s,a)：

式中,σ_s,a为对应于状态-动作元组(s,a)的d维特征列向量，s∈S且a∈ A(s)，维数d明显小于可行的状态-动作元组(s,a)集合的势；θ为维数与σ_s,a相同的可调参数。

令σ_s,a=[σ_s,a(1),… ,σ_s,a(d)]^T ,θ=(θ₁,…,θ_d)^T ,于是:

可以得出关于θ的估计的状态动作值函数的梯度是：

估计函数(7)的性能度量函数为：

式中z_p为不动点，则参数θ的更新公式变为： 式中，α_i,p 为学习系数，设0≤α_i,pσ_s,a(i)≤1; z_p为不动点，则有|z_p-θ′_i|≤|z_p－θ_i|。 2.2 算法设计

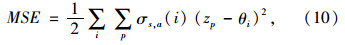
相对于传统的强化学习算法，基于特征表示的强化学习算法更新了d维参数θ。由于状态-动作空间很大，相比之下，特征向量的维数d很小，对克服维数灾难问题是有效的。因此，这里仅仅求解含有d个变量的方程组，而不去求解含有|S×A(S)|个变量的方程组,其中S为交叉口agent的状态的集合，A(S)为状态集合S下的动作的集合。

设某个路网具有m个交叉口，m>1，每个交叉口的入口有j个车道。令s表示某时刻时路网所有交叉口的状态(定义见式(1))组成的全局状态，a为在某时刻时路网所有交叉口的动作(定义见式(3))组成的联合配时动作，r(s,a)为路网在全局状态s及联合配时动作a下所有交叉口的回报值(定义见式(6))之和，根据3.1中基于线性梯度下降法的函数估计思路构建的强化学习算法如下：

(1)初始化θ₀，初始化资格跟踪值e₀=0。

(2)对于每个事件进行赋值：s←每个循环事件的初始状态。

(3)对于所有的a ∈A(s)赋值：

σ_s,a←对应于s,a的特征向量，Q(s,a)←。

(4)根据概率ε，对任意a∈A(s)选择a。

(5)计算：

若a=a，则e←γλ_e(其中γ为折扣因子，λ为资格跟踪参数，e为资格跟踪值);

若a≠a，则对于所有的i∈σ_s,a-，e(i)←0；对于所有的i∈σ_s,a，e(i)←e(i)+1。

(6)执行a，观察立即回报r及下一状态s′，得到时间差分值：δ←r-Q(s,a)。

(7)对于所有a ∈ A(s)赋值：

σ_s′,a←对应于s′，a的特征向量,Q(s,a)←(其中d为σ_s,a的维数)。

(8)根据概率ε，选择。

(9)计算：

(10)回到步骤(4)，直到事件结束。

(11)回到步骤(2)，直到s为终止状态。

虽然算法对参数θ∈R^d(d维实数空间)进行梯度搜索和更新，但是此方法使得对根据Q=σ_s,aθ获得的投影状态动作值函数进行更新，集合{σ_s,aθ|θ∈R^d}形成了|S×A(S)|上所有函数集合的子空间。对于算法的收敛性，存在如下定理：

定理1 对于MDP(见文中第2部分)，其马尔科夫链具有几何遍历性，假定在状态s下选择动作a的概率为π(s,a)=p(a_n=a|s_t=s)>0，特征矩阵中的列σ_s,a(i),i = 1,…,d 线性无关。对于所有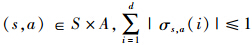,其中d为σ_s,a的维数。则对于所有参数θ ,当时间步n的学习率序列{α(n)}满足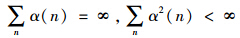时，式(11)以概率1收敛到极限点θ^*，且θ^*满足如下递归关系：

式中，∏_Q为Q的正交映射，H为贝尔曼操作符^[11]。 2.3 特征的表示

特征σ_s,a根据路网中每个信号控制相位的车辆排队长度及绿灯运行时间进行选择。特别地，σ_s,a的选择如下：

式中，q_i为路网在某时刻某相位的车辆排队长度(式(1))；t_i为路网在某时刻某相位的绿灯运行时间(式(1))，σ_a1,...,σ_am对应于m个交叉口中的每个交叉口选择的动作(式(3));N为路网中所有交叉口的相位的数目；L₁和L₂为排队长度的阈值；T₁为绿灯运行时间的阈值。θ与σ_s,a的维数相同。此方法的优势是根据参数化(11)估计状态动作值函数而不是为每个可行的(s,a)元组更新状态动作值函数。在固定策略的情况下，此算法类似于成熟的时序差分算法。使用上述特征的优势是不需要排队长度及绿灯运行时间的完全信息。这里将阈值L₁和L₂ 标注在各相位的车道上并用来判断低交通量(小于L₁)，中等交通量(L₁和L₂之间)，高交通量(大于L₂)。同样，绿灯运行时间能被分为小于阈值T₁ 和大于阈值T₁两种情况。于是，相对于传统的强化学习算法^[6]的优势是不需要精确的排队长度信息。精确的排队长度信息常常很难获得，然而任何时刻有关交通量的高、中、低的特征值很容易获得。基于特征表示的强化学习的实现需要在沿着路网的车道上安装传感器。因为仅需要有关交通拥挤低于阈值L₁，在L₁和L₂之间，或者大于阈值L₂的信息，所以使用两个传感器线圈，其中一个线圈沿着L₁放置，另外一个沿着L₂放置。如果在L₁的传感器没有检测到拥挤，可以推断车道的拥挤水平处于低范围，即低于L₁；如果L₁的传感器检测到拥挤但L₂处的传感器没有检测到，于是拥挤水平可被推断为中等范围(即大于L₁但小于L₂)。同样，如果L₂处的传感器也检测到拥挤，于是能推断拥挤水平处于高范围(即大于或等于L₂)。绿灯运行时间常常被设置在信号交叉口的时间计数器测量到，仅需要有关相位绿灯运行时间是否大于或小于阈值T₁的信息。低于或高于阈值的有关拥挤水平和绿灯运行时间的信息将传给交叉口交通信号控制agent，交叉口交通信号控制agent将会运行基于特征表示的强化学习算法从而获得信号配时策略。基于特征表示的强化学习有一个很短的瞬时相位并且计算效率很高(同时包括时间和空间复杂性),因此在真实系统中容易在线执行并得到信号配时方案。 3 仿真分析 3.1 仿真网络构建

利用Paramics微观交通仿真平台进行仿真。由于Matlab具有丰富的工具箱函数和强大的数据分析能力，能缩短仿真开发周期和保障计算精度，因此应用Matlab实现基于特征表示的强化学习算法。为实现Paramics平台与强化学习算法的交互，通过Paramics提供的丰富的API函数编写C++语言与Matlab的接口，利用Paramics的二次开发接口调用并加载Matlab生成的强化学习算法。在Paramics的Modeler模块中，构建路网(图 1)，设计不同的交通场景，加载强化学习控制算法插件。在Profile文件中设置车流达到分布(图 2)，从而模拟交叉口车流达到的波动特性^[12]。

仿真路网见图 1，由5个交叉口组成，每个交叉口有两个相位，分别为东西直行及右转、南北直行及右转。在算法执行过程中，学习过程经过100次仿真运行(每次仿真运行1 h)后结束。

建立了两种交通需求水平：一种为正常交通需求水平，另一种为高交通需求水平，它考虑到了将来交通量的增长，对正常交通的需求增加了50%。为了更能体现微观交通流波动，对每种需求水平考虑了两种车流到达分布：(1)均匀到达分布(即每10 min释放到路网的车辆数的百分比不变)；(2)非均匀到达分布。车流到达分布定义见图 2，其中非均匀车流到达分布1用于南-北方向需求，非均匀车流到达分布2用于东-西方向需求。参数设置如下：ε=0.03，γ=0.8，λ=0.9，α=0.1,Sp_thr=9 km/h。

3.2 有效性分析

利用车均延误指标来评价基于特征表示的强化学习算法的性能,并与文献^[7]中使用的传统强化学习和定时控制进行比较。

表 1给出了经过仿真运行并收敛后整个路网的基于特征表示的强化学习算法的车均延误。可以看出，在正常交通需求水平下，基于特征表示的强化学习算法的控制效果均比定时控制和文献^[7]的算法好。而在高交通需求水平下，总的车均延误成比例增加。值得注意的是，相对于正常的需求水平情景，在高交通需求水平情景下的非均匀车辆到达分布情况用基于特征表示的强化学习算法控制效果更明显，其车均延误比定时控制和文献^[7]的算法分别减少了63.3%和12.3%。

表 2给出了高交通需求水平下指定交叉口的特征表示的强化学习算法的车均延误。可以看出，基于特征表示的强化学习算法能很好地适应交通条件的变化。与定时控制比较，交叉口3的算法控制效果最好。这主要是因为南北方向的交通需求增加到较高水平而引起了倒流式交通大堵塞，而定时控制采用固定配时策略不能处理交通需求的增加，随后阻止了交叉口上游的车流。

3.3 收敛性分析

图 3和图 4分别反映了在高交通需求水平条件下基于特征表示的强化学习算法在运行5 000周期后学习步数和参数θ与周期数的演变关系。由于本文算法利用了多时间尺度和基于特征表示和线性函数的随机估计思想，其学习步数和参数θ是收敛的。

4 结论

强化学习具有非模型学习算法的优势，为自适应交通信号控制提出了新的模式。将交叉口自适应交通信号控制问题看成马尔科夫决策过程，通过引入基于状态的特征表示法和线性平均函数估计思想，设计了一种改进的强化学习算法。根据路网中每个信号控制相位的车辆排队长度和绿灯运行时间对特征进行选择，减少了计算复杂度。在设置的多交叉口交通环境下，仿真试验表明：此算法在不同的交通需求水平和车流到达分布下均优于定时控制和传统的强化学习算法，更能适应多个交叉口路网的交通变化，并且其参数θ是收敛的。今后将进一步对算法进行理论性分析，并且考虑特征适应方案，从而通过更新特征来获得最好的可能特征。