扩展功能
文章信息
- 严健, 何川, 吴海彬, 汪波, 罗晋明
- YAN Jian, HE Chuan, WU Hai-bin, WANG Bo, LUO Jin-ming
- 基于Peck公式的藏区公路隧道施工地面沉降预测
- Prediction of Ground Settlement for Highway Tunnel Construction in Tibet Based on Peck Formula
- 公路交通科技, 2015, Vol. 31 (1): 110-115
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 110-115
- 10.3969/j.issn.1002-0268.2015.01.018
-
文章历史
- 收稿日期:2014-02-26
2. 西南交通大学 峨眉校区土木系, 四川 峨眉山 614202;
3. 四川高速公路建设开发总公司, 四川 成都 610000
2. Department of Civil Engineering, Emei Campus, Southwest Jiaotong University, Emeishan Sichuan 614202, China;
3. Sichuan Expressway Construction Development Corporation, Chengdu Sichuan 610000, China
国道317线俄尔雅塘至岗托段公路改扩建工程是藏区交通重要的川藏经济走廊中“四路一隧”的重要工程。起于阿坝、甘孜两州交界的俄尔雅塘,止于川藏两省区交界处的岗托大桥,路线全长374.464 km。鉴于线路经过的地区是高原地带的高山峡谷,线路选择大多数沿老路而行。为满足现代城镇的发展需要,国道317线在甘孜州境内,线路改造工程均绕避炉霍、甘孜、德格三县城。在炉霍和甘孜,线路选择了县城河对岸及绕县城折向线路;在德格县,因无路可绕,故选择了2 970 m的德格隧道穿越。
德格隧道位于四川省甘孜州德格县城西北,为新建隧道。设计为单洞两车道,拟建隧道等级为二级公路,宽9.0 m,高5.0 m,全长2 943 m,进口设计高程3 270.53 m,是我国第一条穿越藏区县城居民区的公路隧道。隧址区位于松潘-甘孜地槽褶皱系的玉树-义敦优地槽褶皱带部位。根据区域构造分析,隧址区主要受一系列压扭性断裂构造控制,呈现明显的左行兼逆冲变形特征。该段地形起伏较大,相对高差大于300 m。地形地貌受地层岩性和地质构造控制,多形成陡缓相间的斜坡地形,在绢石千枚岩等分布区形成宽缓的剥蚀槽状地形,在结晶灰岩分布地带常形成鳍脊陡坡、悬崖。区内自然斜坡角一般30°~40°,沟谷纵横、深切,地形陡峻,峰峦起伏。隧道洞口段埋深较浅,约20~40 m,隧道进口位于斜坡下部较缓地带,总体横坡约20°~25°。坡体表层为第四系崩坡积石土,含砾粉质黏土及中风化绢云石英片岩。围岩为三叠系上统图姆沟组上段薄层结晶灰岩。碎石土结构松散、稍密,含砾粉质粘土呈硬塑状;中风化深灰色绢云石英片岩,岩质软弱,受地质构造、风化卸荷影响严重,层间结合差,构造及风化卸荷裂隙发育,岩体破碎,岩体完整性差。K399+375~K399+600段洞口上方需穿越藏式建筑共30多栋,藏区建筑形式以石木结构、毛石结构为主,无基础,体型简单、结构刚度差,见图 1。

|
| 图 1 建筑物与隧道进口照片Fig. 1 Photo of building and tunnel entrance |
采用新奥法施工,采用正台阶开挖,喷锚支护,结构设计拟建采用复合式衬砌。隧道的施工必然会使地表产生沉降,从而对地表房屋产生影响。通过对隧道开挖引起的地表移动和变形进行预测,从而为降低隧道施工对环境的影响提供依据。目前,针对城市地下工程施工,特别是地铁工程的施工引起的地层移动而导致的沉降、位移,受到了国内外众多学者的普遍关注和研究。国内外研究大多集中于城市盾构法隧道施工引起的地面沉降[1] ,计算公式可分为经验公式[2,3,4,5,6,7]和解析解[8] ,其中经验公式使用方便、应用较多。而对于穿越高原狭窄民族聚居区、居民区的公路隧道工程,因其工程施工,其地层移动和地表变形超过一定的限度引起的地面沉陷、隧道破坏、周边建筑物损害等事故,将会产生不良的社会和政治影响,导致严重经济损失。目前该课题的研究较少,因此,正确预测穿越藏区县城居民区的公路隧道施工引起的地表移动及变形十分迫切。
在众多的预测隧道开挖引起的地表位移的经验方法中,Peck法无疑是其中最简便的一个方法,也是截至目前应用最为广泛的方法。然而,由于Peck法是基于有限地区的实测资料提出的经验公式,其预测地层位移的机理尚不清楚,适用性与适用范围也需要进一步分析探讨。根据德格隧道现场实测数据反分析,给出青藏高原东南部地区Peck公式中计算参数的初步建议值;基于实测数据,进一步研究公路隧道地层位移随埋深的分布规律,并对已有公式提出修正,使其在公路山岭隧道建设中具有更为广泛的适用性。韩煊、李宁[5,6]通过对我国8个地区观测数据的分析给出了我国部分地区沉降槽宽度系数k的初步建议值。杨磊[9]就山区隧道施工地表移动与变形规律进行了研究。宋克志、王梦恕等[10]就基于Peck公式的盾构隧道地表沉降的可靠性进行了分析。郭延华、吴龙海[11]等就南京地层地铁隧道施工对Peck公式进行了修正。魏纲[12]收集了12组盾构法隧道施工引起的深层土体沉降实测数据,研究了深层土体沉降槽宽度系数i(z) 随着地层深度z增加产生的变化规律。孙玉永等[13]根据有限元模拟得到了盾构隧道上方不同深度处土层的横向沉降槽曲线。 1 Peck公式及参数
地下隧道的开挖所引起的地层位移曲线一般习惯称之为沉降槽[4]。R.B.Peck(1969)在大量实测资料分析的基础上提出了地面沉降槽近似呈正态分布的概念[1]。其所搜集的其他30多组实测数据都可以较好地采用高斯分布拟合。因此总体上来看,可以认为不论是黏性土还是砂砾石中的隧道开挖,不论是盾构法还是浅埋暗挖法,也不论是全断面法,还是分台阶开挖法,目前搜集的地层位移数据都表明地表沉降曲线基本符合高斯分布规律。Peck认为在不排水情况下,隧道开挖所形成的地面沉降槽的体积应等于地层损失的体积。提出沉降槽的横断面大致遵循高斯分布曲线规律,其相应的地面沉降位移预测模型为:
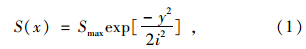
根据O'Reilly和New [3]根据伦敦地区的经验提出的,他们认为i和隧道轴线埋深z0之间存在的简单的线性关系,将式(1)写为包含地层损失率Vl和沉降槽宽度参数K的形式:

定义地层损失率(Volume Loss)Vl为地表沉降槽的面积与隧道开挖的面积A之比,一般以百分比表示。在不排水条件下,地层损失率Vl与最大位移之间的关系可以通过式(1)的积分得到:
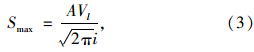
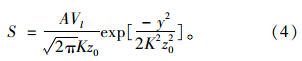
最大沉降量Smax和沉降槽宽度i是Peck沉降槽曲线函数的两个关键参数,它们是工程地质条件、隧道开挖深度、断面尺寸及施工条件等众多因素综合作用的结果。由现场实测结果通过反分析方法求解得到的Smax和i,更准确地代表了实际工程的综合效应[14]。
根据监测数据,采用反分析方法找到一组计算参数x′=(Smax,i),如果这组参数通过反求地面沉降值的结果与实测结果相符,则该组参数即为实际地面沉降计算参数。
设实测点的地面沉降量为Sj(xj),计算沉降量为Sj*(xj),建立目标函数,设(x,S(x))为实测值,最小二乘法就是要找到函数,使得误差平方和达到最小。
将式(1)作如下变换:
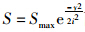 两边取对数得:
两边取对数得:
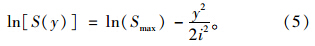
令 y2则有:
y2则有:

建立目标函数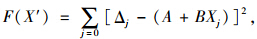 问题转换为求函数最小值,作如下计算:
问题转换为求函数最小值,作如下计算:
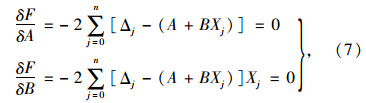
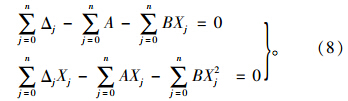
解此方程可得参数A,B,代回前式中即可算得Peck沉降槽曲线函数的两个关键参数最大沉降量Smax和沉降槽宽度i。 2.2 拟合参数的检验
为了评价上述拟合结果,可以借用灰色预测中的检验方法,利用MATLAB软件作为辅助,采用后验差检验对其进行评价[15]。根据地面沉降实测和计算结果,通过定义各测点的位移实测值与计算值之间的残差εj,各测点沉降量计算值的平均值W-和残差平均值ε,各测点沉降量计算值的均方差S12和残差均方差S22,计算后验差比值C和小误差概率P等步骤进行检验。
根据C,P值确定的拟合精度等级表进行精度判定(见表 1)。经过检验,同时拟合精度达到“合格”以上标准时则认为拟合结果有效。
| 等级指数 | 优 | 合格 | 免强 | 不合格 |
| 小误差概率P | >0.95 | >0.80 | >0.70 | ≤0.70 |
| 后验差比值C | <0.35 | <0. 5 | <0. 65 | ≥0.65 |
隧道洞口浅埋段地形、地质条件复杂,围岩基本为软弱破碎岩层,稳定性差,按规定当隧道埋深小于洞跨的3倍时必须进行地表下沉量测[16]。
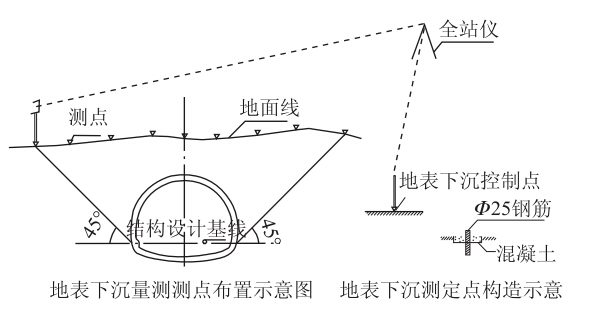
隧道洞顶地表沉降量测点在隧道尚未开挖前就开始布置,以求获得开挖过程中测点全位移曲线。地表下沉量测采用高精度全站仪或精密水准仪进行。测点和拱顶下沉布置在同一断面上,监测断面测点从拱顶中央向两侧左右间隔测点。隧道范围以小间距布点,范围外以稍大间距布点,每个断面不少于7个测点,测点布置如图 2所示。监测频率参照表 2,并根据实际情况确定。
|
| 图 2 地表下沉测点布置示意图Fig. 2 Schematic diagram of arrangement of measuring points of surface subsidence |
| 位移速度/(mm·d-1) | 距工作面距离 | 频度 | 备注 |
| >10 | (0~1)D | 2~4次/1 d | 注:D为隧道宽度 |
| 5~10 | (1~2)D | 1次/1 d | |
| 1~5 | (2~5)D | 1次/2 d | |
| <1 | >5D | 1次/7 d |
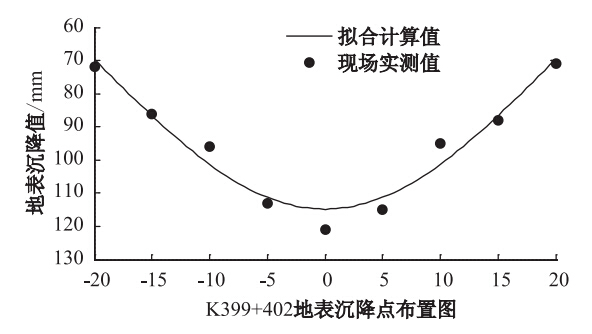
通过地表下沉数据监测数据分析,选用K399+402地表沉降监测数据进行计算,并绘制拟合曲线,见表 3、图 3。对照表 1,可知本次拟合精度为优。
| 监测点 | 横向坐标/mm | 实测沉降量Wj0/mm | 计算沉降值Wjt/mm | 残差εj | Peck方程及参数 |
| 0 | -20 | 72 | 70 | 1.8 | 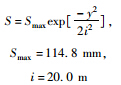 |
| 1 | -15 | 86 | 87 | -1.5 | |
| 2 | -10 | 96 | 102 | -6.5 | |
| 3 | -5 | 113 | 111 | 0.3 | |
| 4 | 0 | 121 | 115 | 4.7 | |
| 5 | 5 | 115 | 111 | 2.3 | |
| 6 | 5 | 95 | 102 | 2.3 | |
| 7 | 5 | 88 | 87 | 2.3 | |
| 8 | 5 | 71 | 70 | 2.3 |
|
| 图 3 K399+402地表沉降数据拟合结果Fig. 3 Fitting curves of surface ground settlement at K399+402 |
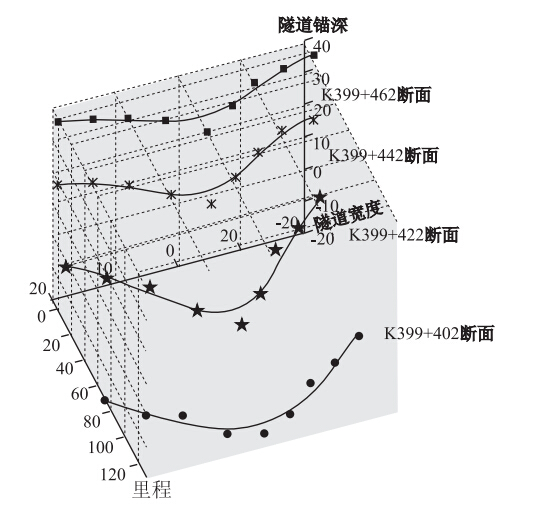
对大量施工监测数据进行了拟合分析,其中4个监测断面的具体拟合结果见表 4、图 4。从计算结果和拟合曲线可以看出,4个监测断面的拟合结果都达到合格以上,其中3个断面的拟合结果达到优秀。由此可见,用Peck法进行隧道地面沉降的横向沉降量空间预测是可行的。
| 里程 | Peck方程拟合 | 残差平均值 | 后验差比值 | 小误差概率 | 拟合精度 |
| K399+402 | Smax=114.8 mm,i=20.0 m | -0.10 | 0.24 | 1 | 优 |
| K399+422 | Smax=75.6 mm,i=11.2 m | -0.44 | 0.23 | 1 | 优 |
| K399+442 | Smax=34.1 mm,i=9.1 m | -0.74 | 0.31 | 1 | 优 |
| K399+462 | Smax=26.4 mm,i=10.3 m | -0.56 | 0.48 | 1 | 合格 |
|
| 图 4 德格隧道进口断面地表沉降拟合结果(单位:m)Fig. 4 Fitting result of surface settlement at entrance of Dege tunnel(unit:m) |
经检验,该方法对横向沉降槽曲线的拟合精度较高,所有断面拟合精度都能合格,且绝大部分断面的拟合精度达到了优。Peck法适用于本区间隧道地面沉降预测,同时也说明藏区公路隧道进口段施工地表沉降的横向分布规律近似于高斯分布。 4 沉降槽宽度和宽度系数的修正与确定
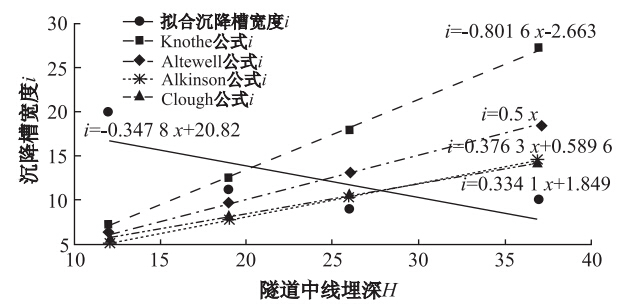
按照表 5中前人提出的i值计算经验公式,对沉降槽宽度i计算经验公式进行修正。以K399+402断面进行计算并与拟合值进行了对比分析,计算结果见表 5和图 5 (隧道计算半径为4.8 m)。
| 公式提出人 | 原沉降槽宽度计算公式 | 适用条件 | 修正系数 | 计算结果/m | 修正值 |
| Knothe |  | 岩石类地层 | 2.76 | 7.24 | 11.79 |
| R.B.perk | i/R=(H/2R)n | 各类土 | n=6.4 | — | 20.02 |
| Attwell,Farmer | i/R=(H/2R) | 黏土 | 3.33 | 6 | 19.98 |
| Atkinson.potts | i=0.25(1.5H+0.5R) | 密实超固结黏土 | 3.92 | 5.10 | 19.99 |
| Clough,Schmidt | i/R=(H/2R)0.8 | 黏土 | 3.48 | 5.74 | 19.98 |
| OReilly,New | i=KH | 各类土 | K=1.67 | — | 20.04 |
|
| 图 5 不同沉降槽计算公式计算及拟合结果(单位:m)Fig. 5 Calculation and fitting results of settlement trough by different formulations(unit:m) |
沉降槽宽度i计算经验公式进行修正后,现进一步计算沉降槽宽度系数k的取值,并最终确定范围,见表 6。
| 里程桩号 | 隧道中线埋深/m | 拟合沉降槽宽度/m | 相应系数k | Knothe公式i | 相应系数k | Attewell公式i | 相应系数k | Atkinson公式i | 相应系数k | Clough公式i | 相应系数k |
| K399+402 | 12 | 20 | 1.667 | 7.2 | 0.603 | 6.0 | 0.500 | 5.10 | 0.425 | 5.74 | 0.478 |
| K399+422 | 19 | 11.2 | 0.589 | 12.4 | 0.653 | 9.5 | 0.500 | 7.73 | 0.407 | 8.29 | 0.436 |
| K399+442 | 26 | 9.1 | 0.350 | 17.9 | 0.691 | 13.0 | 0.500 | 10.4 | 0.400 | 10.65 | 0.410 |
| K399+462 | 37 | 10.3 | 0.278 | 27.2 | 0.735 | 18.5 | 0.500 | 14.5 | 0.392 | 14.12 | 0.382 |
由表 5和表 6可得以下结论:
(1)由于该地区围岩条件变异性较大,沉降槽系数k取值不一。总体上,当围岩以含砾砂岩、黏土等松散堆积体为主时,沉降槽宽度系数较大,能达到1.5~1.8,对于结晶灰岩、石英片岩等完整性较高、自稳能力较好的围岩体,沉降槽宽度系数在0.3~0.6之间。
(2)对于Knothe,Attwell,Farmer等学者提出的沉降槽计算宽度公式,在对公路山岭隧道的应用时需要进行修正。结合本区间隧道不同地表沉降监测断面的地质资料发现,Knothe公式在计算结晶灰岩夹杂含砾砂土的岩体条件下有较好的适用性,见K399+422断面拟合结果(表 6);而Atkinson公式则对黏土、含砾砂岩堆积体适用性较强,见K399+442断面拟合结果。 5 结论
(1)公路山岭隧道运用Peck法进行施工横向地面沉降预测研究是可行的,其沉降槽曲线可以很好地拟合及预测德格隧道施工引起的地面沉降情况。
(2)由表 5可知,Peck提出的沉降槽宽度计算公式中n为待定系数。通过对拟合沉降槽宽度值的反算,可以得出对于本工程待定系数n,从而得到适用于本工程i值计算的修正Peck经验公式。计算得到其n的取值在 0.6~1.3之间,平均可取为 0.8。
(3)对于Knothe,Attwell及Farmer等学者提出的沉降槽计算宽度公式,在对青藏高原东南部地区公路山岭隧道的应用中需要进行修正。其中,Knothe公式在计算结晶灰岩夹杂含砾砂土的岩体条件下有较好的适用性;而Atkinson公式则对黏土、含砾砂岩堆积体适用性较强;其他计算公式都需要引入相应的修正系数。
(4)对于公路山岭隧道,为了使Peck公式更适用,本文建议:当围岩以含砾砂岩等松散堆积体为主时,沉降槽宽度系数较大,能达到1.5~1.8,对于结晶灰岩、石英片岩等完整性较高、自稳能力较好的围岩体,沉降槽宽度系数在0.3~0.6之间。
(5) 采用修正的Peck法关键参数经验公式进行德格隧道地面沉降预测结果显示,受青藏高原东南部特殊地层岩性和地质构造影响,以及构造及风化卸荷造成岩体裂隙发育等因素作用,使该区地面沉降预测结果与城市地铁施工引起的地表沉降结果相反,进口段埋深较浅处地表沉降槽宽度越大,埋深越大沉降槽宽度越小。
| [1] | PECK R B. Deep Excavations and Tunnelling in Soft Ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City:[s.n.],1969:225-290. |
| [2] | MAIR R J,TAYLOR R N,BRACEGIRDIE A. Subsurface Settlement Profiles above Tunnels in Clays [J]. |
| [3] | O'REILLY M P,NEW B M. Settlement above Tunnels in the United Kingdom:Their Magnitude and Prediction [C]// Proceedings of Tunneling 82 Symposium. London:Institution of Mining and Metallurgy,1982:173-181. |
| [4] | ATTEWELL P B,YEATES J,SELBY A R. Soil Movements Induced by Tunnelling and Their Effects on Pipelines and Structures[M]. Glasgow:Blackie and Son Ltd.,1986:10-50. |
| [5] | 韩煊,李宁,STANDING J R. 地铁隧道施工引起地层位移规律的探讨[J]. 岩土力学,2007(3):609-613. HAN Xuan,LI Ning,STANDING J R. Study on Subsurface Ground Movement Caused by Urban Tunneling [J]. Rock and Soil Mechanics,2007(3):609-613. |
| [6] | 韩煊. 隧道施工引起地层位移及建筑物变形预测的实用方法研究 [D].西安:西安理工大学,2007. HAN Xuan. Ground Displacement and Building Deformations Induced by Urban Underground Construction: Practical Prediction Methods [D]. Xi'an:Xi'an University of Technology,2007. |
| [7] | 姜忻良,赵志民,李圆.隧道开挖引起土层沉降槽曲线形态的分析与计算[J ].岩土力学,2004,25(10):1542-1544. JIANG Xin-liang,ZHAO Zhi-min,LI Yuan. Analysis and Calculation of Surface and Subsurface Settlement Trough Profiles due to Tunneling [J]. Rock and Soil Mechanics,2004,25(10):1542-1544. |
| [8] | 魏纲.盾构法隧道施工引起的土体变形预测[J]. 岩石力学与工程学报,2009,28(2):418-424. WEI Gang. Prediction of Ground Deformation Induced by Shield Tunneling Construction[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(2):418-424. |
| [9] | 杨磊.山区隧道施工地表移动与变形规律研究[D].长沙:长沙理工大学,2008. YANG Lei. Research about the Regularization of Ground Surface Movement and Deformation Caused by Mountain Tunnel Excavation[D]. Changsha:Changsha University of Science & Technology,2008. |
| [10] | 宋克志,王梦恕,孙谋. 基于Peck 公式的盾构隧道地表沉降的可靠性分析[J].北方交通大学学报,2004(8):30-33. SONG Ke-zhi,WANG Meng-shu,SUN Mou. Reliability Analysis of Ground Settlement with Shield Tunnel Construction Based on Peck Formula [J]. Journal of Northern Jiaotong University,2004(8):30-33. |
| [11] | 郭延华,吴龙海. 南京地层地铁隧道施工的Peck公式修正 [J]. 河北工程大学学报:自然科学版,2013(3):41-44. GUO Yan-hua,WU Long-hai. The Correction of Peck Formula in Subway Tunnel under Nanjing Stratum[J]. Journal of Hebei University of Engineering:Natural Science Edition,2013(3):41-44. |
| [12] | 魏纲.盾构隧道深层土体沉降槽宽度系数计算方法研究[J].公路交通科技.2010,27(4):110-115. WEI Gang. Study on Calculation Method of Width Coefficient of Subsurface Settlement Trough in Shield Tunnel[J]. Journal of Highway and Transportation Research and Development. 2010,27 (4):110-115. |
| [13] | 孙玉永,周顺华,宫全美.软土地区盾构掘进引起的深层位移场分布规律[J]. 岩石力学与工程学报,2009,28(3):500-506. SUN Yu-yong,ZHOU Shun-hua,GONG Quan-mei. Distribution of Deep Displacement Field during Shield Tunneling in Soft-soil Areas [J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(3):500-506. |
| [14] | 阳军生,刘宝深.城市隧道施工引起的地表移动及变形[M].北京:中国铁道出版社,2002:2-6. YANG Jun-sheng,LIU Bao-shen. The Movement and Deformation of Surface Caused by Tunnel Construction in City[M]. Beijing:China Railway Publishing House,2002:2-6. |
| [15] | 赵志民.隧道施工引起土体位移与应力的镜像理论研究以及回归方法的应用[D].天津:天津大学,2004. ZHAO Zhi-min. Study of Image Theory and Application of Regression Method of Tunneling Induced Soil Displacements and Stresses [D]. Tianjin:Tianjin University, 2004. |
| [16] | 王建宇. 隧道工程监测和信息化设计原理[M]. 北京:中国铁道出版社,1990. WANG Jian-yu. Tunnel Engineering Monitoring and Information Design Principle[M]. Beijing:China Railway Publishing House,1990. |
 2015, Vol. 31
2015, Vol. 31
