扩展功能
文章信息
- 陈驰, 刘成清, 陈林雅, 赵世春
- CHEN Chi, LIU Cheng-qing, CHEN Lin-ya, ZHAO Shi-chun
- 落石作用于钢筋混凝土棚洞的冲击力研究
- Study on Impact Force of Rock-fall onto Rock Shed Tunnel
- 公路交通科技, 2015, Vol. 31 (1): 102-109
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 102-109
- 10.3969/j.issn.1002-0268.2015.01.017
-
文章历史
- 收稿日期:2014-03-11
我国地理地形多变复杂,易诱发滑坡、崩塌落石、泥石流等自然灾害。在公路、铁路、城镇附近发生落石灾害,危害很大。为此,通常是建立明洞、棚洞、防护网等被动防护结构。钢筋混凝土棚洞是有效的一种防护结构,它由钢筋混凝土框架及钢筋混凝土顶板构成,在顶板上覆盖有缓冲作用的垫层[1,2],见图 1。

|
| 图 1 钢筋混凝土棚洞工程实例Fig. 1 Engineering example of RC shed tunnel structure |
近年来,在钢筋混凝土棚洞冲击响应的研究中,有对钢筋混凝土棚洞滚石冲击碰撞系数及动力响应研究[3,4,5]。针对落石冲击力算法,国内可参考的有公路路基规范[6]、铁路隧道手册[7]、杨其新[8]、刘茂[9]及叶四桥[10]等提出的冲击力计算方法。国外有日本道路公团[11]及瑞士方法[12]。将各种计算方法比较得知[13],国内的计算方法得到落石的平均冲击力,结果偏小。Pichler[14]试验表明,日本和瑞士的计算方法虽符合实际,但不能反映缓冲层厚度及冲击角度变化对落石冲击力的影响,计算结果存在一定误差。
落石冲击钢筋混凝土棚洞实际上是一个很复杂的过程,影响冲击力大小的因素包括落石的形状、质量、冲击速度、垫层材料、厚度、棚洞结构的刚度等因素。结合冲量定理研究最大冲击力的近似计算方法,然后采用动力有限元软件LS-DYNA,以落石的形状、质量、冲击速度、垫层材料、厚度以及棚洞跨度等6个主要的影响因素为变量,研究落石冲击力大小。根据有限元分析结果确定计算公式中的参数取值,将计算公式与已有试验结果进行对比,表明该公式的合理性,为今后防护棚洞的设计提供可靠的理论依据。 1 落石冲击力近似计算方法的研究
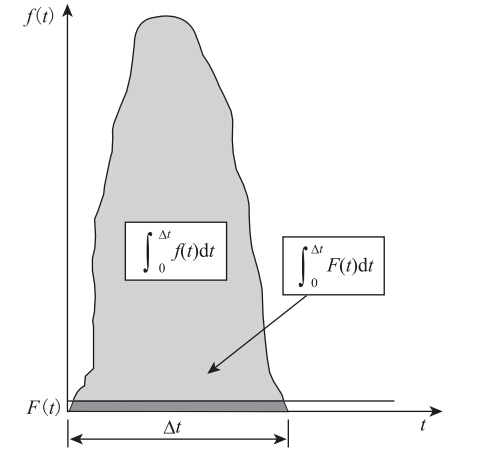
由于落石冲击缓冲垫层的复杂性,影响冲击力的因素很多,考虑的主要影响因素有:落石的形状、质量、冲击速度、垫层材料、厚度以及棚洞跨度。在碰撞过程中做出如下假设:(1)落石正碰于缓冲垫层;(2)不考虑冲击过程中落石的转动、分解和土层飞溅的影响。根据图 2所示的AZZOIN落石弹跳冲量模型[15],假设碰撞发生的时刻为0,碰撞过程中的冲量可表示为:
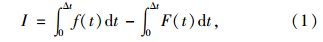
|
| 图 2 AZZONI落石弹跳冲量模型Fig. 2 AZZONI Rock-fall spring impulse model |
落石冲击法向恢复系数定义为:

根据冲量定理
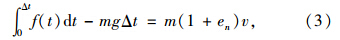

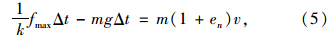
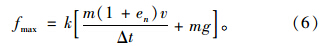
根据前面的简化,冲击时间受落石形状、质量、冲击速度、垫层材料、垫层厚度及跨度的影响。由于落石形状、垫层材料对时间的影响较为复杂,因此通过采用修正系数来反应其对时间的影响。则冲击时间可以用函数表示为:
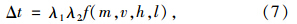
由式(6)和式(7)知,若确定了系数k,λ1,λ2,en的取值及f(m,v,h,l)的表达式,即可求出最大冲击力。下面通过数值模拟,研究落石形状、质量、冲击速度、垫层材料、垫层厚度以及棚洞跨度等因素对冲击力的影响。 2 落石冲击下钢筋混凝土棚洞动力响应的数值模拟 2.1 问题描述
以实际工程中典型的棚洞建立计算模型,考虑棚洞的对称性,在冲击作用下落石的能量大部分由冲击位置所在的跨度所吸收,因此以单跨棚洞模型为研究对象。该单跨棚洞宽度为3 m,棚洞板的厚度为0.4 m,混凝土强度等级为C30,钢筋强度等级为HRB335。 2.2 模型的材料参数
混凝土采用Johnson-Holmquist本构模型[16],该模型适用于混凝土承受大应变、高应变率和超压等场合,等效强度用超压、应变率和损伤程度来表达,参数的取值见表 1。其中,A为材料内聚强度;B为压力硬化系数;C为材料应变率硬化系数;N为压力硬化指数;Fc为混凝土单轴抗压强度;T为材料能承受的最大拉伸应力; εminf为最小断裂应变;Smax为归一化无量纲等效应力最大值;PC为单轴试验中的压力;UC为单轴压缩试验的体积应变;PL为单轴试验中的拉力;UL为单轴拉伸试验的体积应变;D1,D2为损伤因子;K1,K2 ,K3为与应变率有关的量。
| ρ0/(g·cm-3) | G/GPa | A | B | C | N | FC/MPa | T/MPa | εminf | Smax |
| 2.4 | 12.53 | 0.27 | 1.86 | 0.007 | 0.84 | 33.67 | 2.4 | 0.01 | 11 |
| PC/MPa | UC | PL/MPa | UL | D1 | D2 | K1/GPa | K2/GPa | K3/GPa | |
| 162.0 | 0.009 | 950 | 0.1 | 0.04 | 1 | 620 | 400 | 260 |
钢筋采用理想弹塑性模型,即达到屈服强度后应力应变曲线为一水平段,E为弹性模量,Py为屈服强度。垫层材料采用DP模型,相关参数见表 2。 考虑垫层材料刚度相对较小,落石假定为刚体,由于动力性能的原因会造成冲击力的计算结果比实际略大,特别当落石速度较高时,数值计算中增量步步长的增加使得求解误差增大。通常,落石的速度控制在5~25 m/s范围内[17],在落石速度较大时通过减小增量步及细化网格的方法降低所引起的误差。落石的密度为2.5 g/cm3。
| 类型 | ρ/(g·cm-3) | E/MPa | μ | φ | c/MPa | py/MPa |
|
土垫层 砂垫层 |
1.8 2.0 |
25.0 39.0 |
0.2 0.3 |
27.0° 34.0° |
0.024 0.040 |
0.14 0.20 |
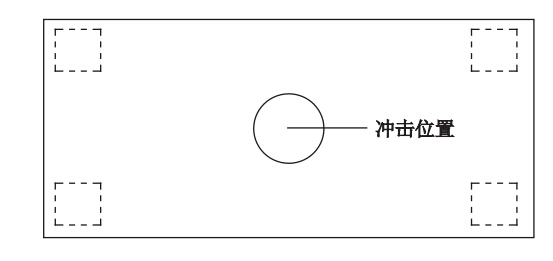
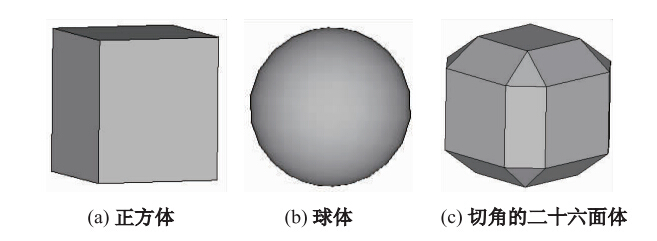
假定落石冲击位置为棚洞的中心处,见图 3,设定基本参数为:落石的形状为球体,半径为0.5 m,对应落石的质量M0=1.3 t,冲击速度V0=12 m/s,垫层材料为土垫层,垫层厚度H0=0.5 m,棚洞跨度L=8 m。采用单因素控制方法,即研究某影响因素时其他变量均按基本参数设置。由于通常的工程中,为避免钢筋混凝土棚洞发生破坏,避免产生过大的塑性变形,通常按弹性设计,因此在弹性范围内通过分别改变落石形状、质量、冲击速度、垫层材料、垫层厚度及跨度来研究冲击力的变化情况。落石形状为正方体、球体、切角的二十六面体(图 4),假定正方体和切角的二十六面体形状的落石与垫层的接触面为其底面;质量的取值分别为0.7,1.0,1.3,1.6,1.9 t;速度的取值分别为6,9,12,15,18 m/s;垫层材料为土垫层以及砂垫层;垫层厚度的取值分别为0.3,0.4,0.5,0.6,0.7,0.8 m;棚洞跨度的取值分别6,7,8,9,10 m。
|
| 图 3 棚洞的冲击位置Fig. 3 Impact position of rock shed tunnel |
|
| 图 4 落石的形状Fig. 4 Shapes of rock-fall |
混凝土、垫层及落石均采用solid164单元,钢筋采用beam161单元。对于落石的每种冲击情况,均设置一个动态显示分析步。仿真过程中设置的求解时间为0.1 s,计算结果文件输出步数和时间历程文件输出步数均为200。对模型的柱底约束其所有自由度。采用LS-DYNA动力求解器,落石与垫层的接触设为自动面面接触,动摩擦系数和静摩擦系数均为0.5,阻尼比取0.03,计算方法为拉格朗日算法。 3 落石冲击力的数值计算结果 3.1 落石形状对冲击力的影响
不同落石形状下,落石冲击力与时间的关系见图 5。可看出,与球体相比,当落石的形状为正方体和切角的二十六面体时,冲击力在很短的时间达到了最大值,分别为2 035 kN和988 kN,而当落石形状为球体时,最大冲击力为667 kN。落石为正方体、二十六面体、球体时与其相对应的冲击时间分别为0.018 5,0.038 0,0.053 5 s。另外,在形状为球体与二十六面体的冲击作用下,曲线出现了一定的震荡现象。以上数据表明,落石形状对冲击力及冲击时间的影响较大,当落石与缓冲垫层接触时,初始接触面积的增加会导致冲击力的迅速增大。
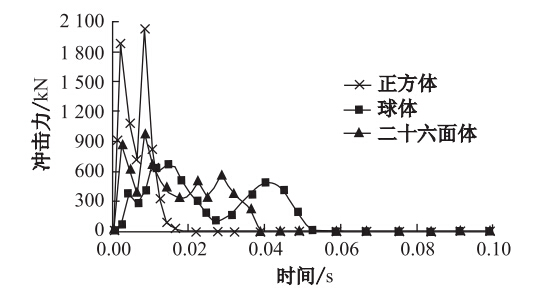
|
| 图 5 不同形状下冲击力与时间的关系Fig. 5 Relations between impact force and impact duration in different rock-fall shapes |
为使本文研究内容与他人的试验有可比性,接下来的数值模拟所选的落石形状,均采用球体。 3.2 落石质量对冲击力的影响
不同质量下,落石冲击力与时间的变化关系见图 7,从中可看出,整个冲击过程非常短暂,当质量从0.7 t变化至1.9 t时,冲击力均在很短的时间内达到了最大值,之后又迅速减小,在出现一次震荡现象后减小为0,达到最大值的时刻均在0.015 s左右,此时的冲击力分别为404,511,667,778,855 kN。随着质量的增加,冲击时间有所增加,分别为0.045 5,0.049 5,0.053 5,0.056 0,0.059 0 s。这说明,落石质量的变化会引起冲击时间的变化,但不会影响冲击过程的总体趋势。

|
| 图 6 不同质量下冲击力与时间的关系Fig. 6 Relations between impact force and impact duration in different masses |
不同冲击速度下,落石冲击力与时间的关系曲线见图 7,从中可看到,落石冲击力随时间变化的总体趋势仍然是一致的,当速度从6 m/s变化到18 m/s 时,冲击力达到最大值的时间逐渐减小,分别为0.022 5,0.017 0,0.014 5,0.012 0,0.010 0 s。此时最大冲击力分别为302,470,667,940,1 250 kN,与落石的冲击速度近似成比例关系。在不同的冲击速度下,冲击时间均在0.053 0 s左右。这说明,不同的冲击速度基本不影响整个冲击时间,但会影响冲击力达到最大值的时间。
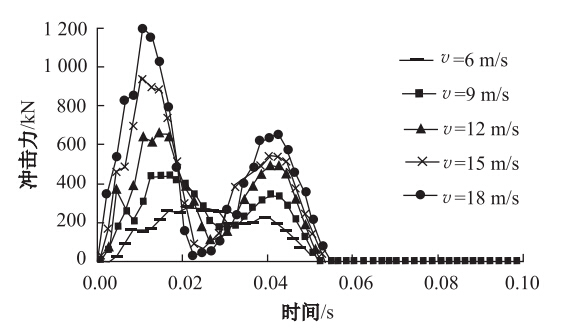
|
| 图 7 不同冲击速度下冲击力与时间的关系Fig. 7 Relations between impact force and impact duration in different impact speeds |
不同垫层材料下,落石冲击力与时间的变化情况见图 8。可看出,当缓冲层分别为土垫层和砂垫层时,对应的最大冲击力分别为667 kN和1 058 kN,冲击时间则分别为0.053 5 s和0.040 5 s。这说明,不同垫层材料对最大冲击力影响也较大,缓冲性能好的材料,可以增加冲击时间,并能有效降低冲击力。

|
| 图 8 不同垫层材料下冲击力与时间的关系Fig. 8 Relations between impact force and impact duration in different cushion materials |
不同垫层厚度下,落石冲击力与时间的关系见图 9。土垫层厚度从0.3 m变化到0.8 m时,冲击力的整体趋势仍保持一致,冲击力达到最大值的时刻也大致相同。此时的冲击力分别为1 026,822,667,622,579,547 kN。可看到,随着垫层厚度的增加,最大冲击力减小幅度越来越低,当垫层厚度为0.7 m和0.8 m时,最大冲击力分别为579 kN和547 kN,两者差距很小。随着垫层厚度的增加,冲击时间随之增加。表明增加垫层厚度可一定程度上增大冲击时间,减小冲击力,但盲目地增大砂垫层厚度不仅不能起到减小冲击力的作用,反而会增加结构的自重,造成材料的浪费。
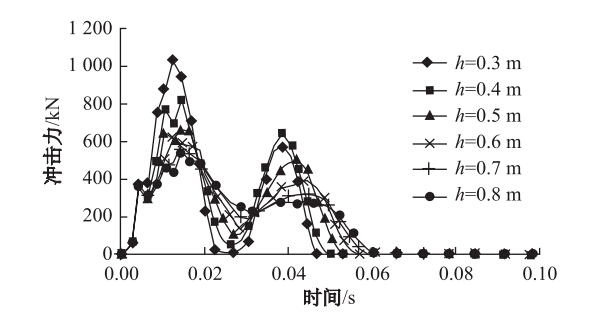
|
| 图 9 不同垫层厚度下冲击力与时间的关系Fig. 9 Relations between impact force and impact duration in different cushion thicknesses |
不同跨度下,落石冲击力与时间的关系如图 10,从中可发现,随着跨度的增加,整个冲击过程的前半段冲击力时间曲线几乎重合,仅仅是在冲击过程的后半段而有所不同,并且最大冲击力均在680 kN左右。冲击时间随跨度的增加而略有增加。这说明,跨度的增加略微增加冲击作用时间,不会影响最大冲击力。由于冲击过程非常短暂,落石的冲击能量来不及扩散出去,导致在前半阶段冲击力与时间的关系曲线有着相同的变化情况。
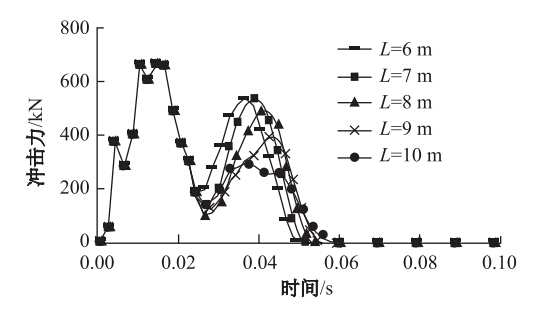
|
| 图 10 不同跨度下冲击力与时间的关系Fig. 10 Relations between impact force and impact duration in different span lengths |
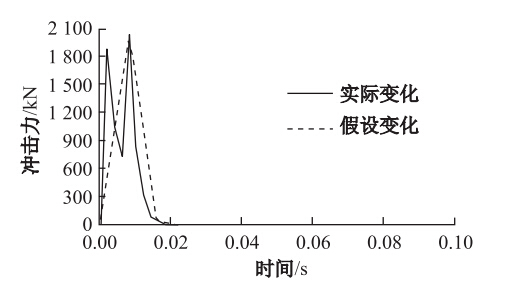
从上面的分析中可看出,当落石形状为球体时,在其他因素的影响下,落石冲击力的变化规律大致相同,即在很短的时间冲击力达到最大值,之后迅速减小,在出现一次震荡现象后减小为0。现再次考虑不同形状下冲击力的变化情况。冲击力随时间变化的曲线分别如图 11~图 13所示,并分别连接冲击起始时间点与最大冲击力点、结束时间点与最大冲击力点,作一条假设的冲击力随时间变化的曲线。从中可以看出,时间轴分别与假设变化的曲线和实际变化的曲线所围成的面积近似相等,由于面积表示的物理意义为冲量的大小,因此落石与钢筋混凝土棚洞接触过程中的冲量可以近似表示为:
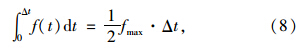
|
| 图 11 落石形状为正方体时冲击力与时间的关系Fig. 11 Relations between impact force and impact duration in cube shape |
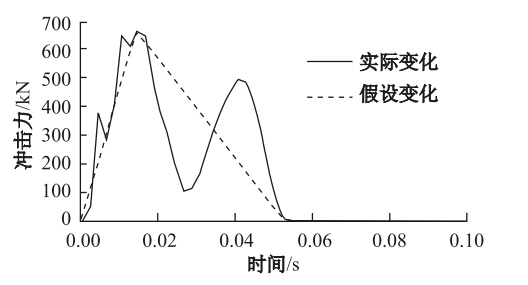
|
| 图 12 落石形状为球体时冲击力与时间的关系Fig. 12 Relations between impact force and impact duration in sphere shape |

|
| 图 13 落石形状为二十六面体时冲击力与时间的关系Fig. 13 Relations between impact force and impact duration in 26 polyhedral shape |
在研究落石运动规律过程中,滚石的碰撞恢复系数是重要的控制参数,它不仅与落石的冲击速度、质量有关,还与落石、地面覆盖层的物理力学性质密切相关,目前尚无合理的计算理论,这是落石灾害研究的一个难点问题。目前,已有较多的各种坡表地质条件下的法向碰撞恢复系数研究[18,19]。一般法向恢复系数多在0.1~0.5之间,依据落石发生碰撞坡表的软硬不同进行取值,对于坚硬的坡表取高值,对于越软的坡表取低值。考虑到冲击速度、垫层材料、厚度等因素的影响,数值模拟得到落石的法向碰撞恢复系数在0.1~0.2之间,结合文献[20]给出的不同坡面条件法向碰撞恢复系数的建议取值,en的值可取为 0.1~0.15。 3.9 冲击时间的确定
由上述分析可知,冲击时间主要受落石形状、质量、垫层材料、垫层厚度及跨度的影响,冲击速度对冲击时间的影响很小。考虑到图 12中棚洞跨度略微影响到冲击时间,对实际工程中最为关心的最大冲击力的几乎不影响,因此可忽略跨度对冲击时间的影响。图 14给出了不同质量及垫层厚度下冲击时间的变化情况。根据图 14的结果,将质量及垫层厚度对时间的影响进行拟合,结合图 5和图 8中落石形状及垫层材料对冲击时间的影响情况,则式(7)变为:
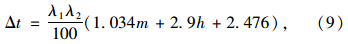

|
| 图 14 不同质量以及垫层厚度下的冲击时间Fig. 14 Impact durations in different masses and cushion thicknesses |
将k的值及式(9)代入式(6)得到考虑了落石形状、质量、垫层材料、垫层厚度以及跨度等因素的落石作用下钢筋混凝土棚洞最大冲击力为:
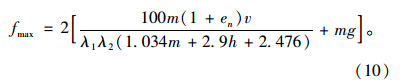
杨其新等[7]基于室内试验建立了一套经验公式,考虑缓冲层厚度对冲击力的影响。由于该式对冲击时间的计算较准确,而实际求得的冲击力为冲击过程平均冲击力,因此将冲击时间公式(式(9))与文献[7]的试验值进行比较。为与试验一致,落石形状采用二十六面体,垫层材料为土垫层,结果见表 3。
| 编号 | 落石质量/t | 下落高度/m | 垫层厚度/m | 本文计算值/(×10-2 s) | 文献[7]推导值/(×10-2 s) | 误差/% |
| 1 | 0.5 | 2.0 | 0.3 | 2.47 | 2.37 | 4.30 |
| 2 | 1.0 | 4.0 | 0.4 | 2.99 | 3.07 | 2.49 |
| 3 | 1.5 | 6.0 | 0.5 | 3.51 | 3.77 | 6.96 |
| 4 | 2.0 | 8.0 | 0.6 | 4.02 | 4.47 | 10.06 |
| 5 | 2.5 | 10.0 | 0.7 | 4.54 | 5.18 | 12.33 |
可看出冲击时间计算结果与试验结果基本一致,说明提出的冲击时间计算公式能较准确的反映落石作用于钢筋混凝土棚洞的冲击时间。
下面将落石作用下钢筋混凝土棚洞最大冲击力(式(10))与落石冲击力的试验结果[13]进行比较。根据试验情况,落石的形状可取为二十六面体,缓冲层为砂垫层,法向恢复系数取0.1,结果见表 4。由表 4可看出,采用本文计算方法与试验结果吻合较好,说明提出的落石作用下钢筋混凝土棚洞最大冲击力公式可以用于确定落石作用下钢筋混凝土棚洞最大冲击力,基本能满足设计精度要求。
| 落石质量/t | 下落高度/m | 冲击速度/(m·s-1) | 冲击时间/s | 本文计算值/kN | 文献[13]试验值/kN | 误差/% |
| 10.16 | 2.00 | 6.26 | 0.073 | 1 938 | 1 720 | 12.7 |
| 10.16 | 8.55 | 12.95 | 0.073 | 3 794 | 3 520 | 7.8 |
| 18.26 | 8.62 | 13.00 | 0.112 | 4 944 | 5 080 | 2.7 |
| 18.26 | 18.67 | 19.13 | 0.112 | 7 233 | 8 490 | 14.8 |
| 18.26 | 18.85 | 19.22 | 0.112 | 7 266 | 8 270 | 12.1 |
以冲量定理和有限元法相结合的方法,推导出考虑了落石形状、质量、冲击速度、垫层材料、垫层厚度以及棚洞跨度等各种因素的落石作用于钢筋混凝土棚洞的冲击力公式,并用试验数据验证了该公式的合理性,可为钢筋混凝土棚洞在落石冲击作用下的防灾设计提供理论依据。同时发现,落石形状、质量、垫层材料及垫层厚度对冲击力和冲击时间的影响较大,冲击速度对冲击力的影响较大,对冲击时间的影响较小,棚洞跨度略微影响冲击时间,几乎不影响最大冲击力。
| [1] | OLSSON R. Analytical Prediction of Large Mass Impact Damage in Composite Laminates[J]. |
| [2] | 蒋树屏. 山区公路大跨异型棚洞结构[M].北京:科学出版社,2009. JIANG Shu-ping. Large-span Heterotypic Shed Structure of Mountain Highway [M]. Beijing:Science Press,2009. |
| [3] | 何思明,吴永,杨雪莲.滚石坡面冲击回弹规律研究[J]. 岩石力学与工程学报,2008,27(增1):2793-2798. HE Si-ming,WU Yong,YANG Xue-lian. Study of Rock-fall Motion on Slope[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(S1):2793-2798. |
| [4] | 何思明,沈均,吴永.滚石冲击荷载下棚洞解结构动力响应[J]. 岩土力学,2011,32(3):781-788. HE Si-ming,SHEN Jun,WU Yong. Rock Shed Dynamic Response to Impact of Rock-fall[J]. Rock and Soil Mechanics,2011,32(3):781-788. |
| [5] | 刘成清,陈驰. 落石冲击作用下钢筋混凝土棚洞结构的动力系数研究[J]. 施工技术,2014,43(17):46-49. LIU Cheng-qing,CHEN Chi. Study on the Dynamic Coefficient of Rock Shed under Rock-fall Impact[J]. Construction Technology,2014,43(17):46-49. |
| [6] | 铁道部工务局. 铁路工务技术手册——路基[M].北京:中国铁道出版社,1995. Works Bureau of Railway Ministry. Railway Technical Manual:Subgrade[M]. Beijing:China Railway Publishing House,1995. |
| [7] | 铁道部第二设计院.铁道工程设计技术手册——隧道[M]. 北京:人民铁道出版社,1978. The Second Railways Survey and Design Institute. Manual of Railway Engineering Design:Tunnel [M]. Beijing:China Railway Publishing House,1978. |
| [8] | 杨其新,关宝树. 落石冲击力计算方法的试验研究[J]. 铁道学报,1993,18(1):101-106. YANG Qi-xin,GUAN Bao-shu. Test and Research on Calculating Method of Falling Stone Impulsive Force[J]. Journal of China Railway Society,1993,18(1):101-106. |
| [9] | 刘茂.基于弹塑性修正Hertz接触理论的落石冲击力计算方法[J]. 中国地质灾害与防治学报,2012,23(3):21-27. LIU Mao. Calculation of Impact Force of Falling Rock Based on Elastoplastic Modified Hertz Contact Theory[J]. The Chinese Journal of Geological Hazard and Control,2012,23(3):21-27. |
| [10] | 叶四桥,陈洪凯,唐红梅. 落石冲击力计算方法[J]. 中国铁道科学,2010,31(6):56-62. YE Si-qiao,CHEN Hong-kai,TANG Hong-mei. The Calculation Method for the Impact Force of the Rockfall[J]. China Railway Science,2010,31(6):56-62. |
| [11] | KAWAHARA S,MURO T. Effects of Dry Density and Thickness of Sandy Soil on Impact Response due to Rock Fall[J]. |
| [12] | LABIOUSE V,DESCOEUDRES F,MONTANI S. Experimental Study of Rock Sheds Impacted by Rock Blocks [J]. Structural Engineering International,1996,3(1):171– 175. |
| [13] | 叶四桥,陈洪凯,唐红梅. 落石冲击力计算方法的比较研究[J]. 水文地质工程地质,2010,37(2):59-64. YE Si-qiao,CHEN Hong-kai,TANG Hong-mei. Comparative Research on Impact Force Calculation Methods for Rockfalls [J]. Hydrogeology &Engineering Geology,2010,37(2):59-64. |
| [14] | PICHLER B,HELLMICH C,MANG H A. Impact of Rocks onto Gravel Design and Evaluation of Experiments[J]. |
| [15] | AZZONI A,LA BARBERA G,ZANINETTI A. Analysis and Prediction of Rockfalls Using a Mathematical Model [J]. |
| [16] | 熊益波,陈剑杰,胡永乐,等.混凝土Johnson-Holmquist本构模型关键参数研究[J].工程力学,2012,29(1):121-127. XIONG Yi-bo,CHEN Jian-jie,HU Yong-le,et al. Study on the Key Parameters of the Johnson-Holmquist Constitutive Model for Concrete[J]. Engineering Mechanics,2012,29(1):121-127. |
| [17] | DUFFY J D. Field Tests and Evaluation of Hi-tech Low Energy Chain in Rockfall Fences,Record No. CA/05-96-02[R]. San Luis Obispo,CA: California Department of Transportation,1996. |
| [18] | 何思明,吴永,李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学,2009,30(3):623-627. HE Si-ming,WU Yong,LI Xin-po. Research on Restitution Coefficient of Rock Fall[J]. Rock and Soil Mechanics,2009,30(3):623-627. |
| [19] | 唐红梅,鲜学福,王林峰,等. 基于小波变换的碎石土垫层落石冲击回弹系数试验[J]. 岩土工程学报,2012,34(7):1278-1282. TANG Hong-mei,XIAN Xue-fu,WANG Lin-feng,et al. Coefficient of Resilience for Rock Fall onto Gravel Soil Cushion Based on Wavelet Transform Theory [J]. Chinese Journal of Geotechnical Engineering,2012,34(7):1278-1282. |
| [20] | 叶四桥. 隧道洞口段落石灾害研究与防治[D]. 成都:西南交通大学,2008:75-119. YE Si-qiao. Research and Mitigation of Rockfall Hazards at Tunnel Entrance and Exit[D]. Chengdu:Southwest Jiaotong University,2008:75-119. |
 2015, Vol. 31
2015, Vol. 31
