扩展功能
文章信息
- 王学伟, 卜一之, 祝兵, 谢明志, 贾少敏
- WANG Xue-wei, BU Yi-zhi, ZHU Bing, XIE Ming-zhi, JIA Shao-min
- 六塔斜拉桥主梁制造阶段参数敏感性研究
- Analysis on Parameter Sensitivity at Manufacturing Stage of Main Beam of 6-pylon Cable-stayed Bridge
- 公路交通科技, 2015, Vol. 31 (1): 76-82
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 76-82
- 10.3969/j.issn.1002-0268.2015.01.013
-
文章历史
- 收稿日期:2013-11-26
2. 西南交通大学 峨眉校区土木工程系, 四川 峨眉山 614202
2. Department of Civil Engineering, Emei Campus, Southwest Jiaotong University, Emeishan Sichuan 614202, China
斜拉桥的不断发展对施工控制带来了极大的挑战,而斜拉桥施工控制过程是一个繁琐的系统控制工程,施工工序众多,施工周期较长,对控制质量和精度要求高,施工监控难度更大,多种因素导致误差累积,施工过程中误差调整量有限,且调整难度较大,误差累积会对施工阶段和运营阶段带来安全隐患,因而有必要对施工控制手段提出更高要求。以传统的施工控制手段为基础,结合全过程的控制理念和几何控制理念,大力发展较为完善合理的控制方法迫在眉睫。基于几何控制法的全过程施工控制在获得高精度斜拉索索力和主梁标高等关键施工控制量方面有着显著的优势[1]。
由于制造阶段加工水平和施工阶段施工环境等双重因素的影响,大跨斜拉桥在施工过程各阶段的实际状态与目标设计状态总是存在一定的偏差,如何实现两者之间的偏差最小是施工控制的目的,因此,要想达到这一目的,除了需要获得准确的结构计算分析结果外,还必须要采取一定的措施消除各种误差带来的影响[2]。参数敏感性的分析是对系统输出做模型参数、模型输入或初始条件修改变化的敏感度(抑或灵敏度)研究[3, 4, 5, 6, 7]。参数敏感性的分析量化了桥梁施工阶段的力学行为同结构参数不断变化间的联系,因此给桥梁结构敏感性参数的选取提供了一定的科学依据[8, 9, 10],同时也为敏感性参数的识别与有限元模型修正、参数分析预测和误差的调整等研究工作提供必备的理论基础。
本文以嘉绍跨江公路大桥为工程实例,利用有限元软件建立考虑施工全过程的全桥有限元模型,以结构设计参数为基准,充分考虑几何非线性的影响,基于几何控制法原理详细探讨了主梁关键制造参数变化对其结构力学行为(包括主梁线形、拉索索力、塔偏、结构应力等)的影响,从而确定主梁制造参数变化对结构的影响程度。同时本文对主梁制造参数误差进行了实测统计,确定了主梁制造参数变化的取值,为同类桥梁理论分析中参数的选取具有一定的借鉴意义。
1 基于几何控制的敏感性分析方法
几何控制的理论基础可以概括为:几何体系一定的弹性结构于某一时刻在内力和变形上的状态唯一取决于这一时刻结构所承受的作用体系,而与此前的结构构件安装历程顺序、作用施加及变迁过程无关[11]。其原因归于,此刻结构在变形和内力上的状态可由变形协调方程及静力平衡方程确定。
本文以嘉绍跨江公路大桥为研究对象,探讨主梁关键制造参数变化对主梁成桥线形及斜拉索成桥索力的影响。具体分析思路如下:
(1)确定基准状态有限元模型。考虑在施工全过程中的几何非线性特性,采用结构基准参数建立基于施工全过程的基准模型,进而获得塔柱与主梁的无应力状态和斜拉索的无应力构形等几何参数量。
(2)确定参数敏感度分析模型。基于基准状态有限元模型,根据所研究的主梁关键制造参数发生变化对分析模型进行修改,同时确保其他结构参数同基准模型一致。其中,主梁自重变化是通过修改单元自重荷载来实现;主梁制造长度变化和主梁夹角变化是通过修改基准状态下主梁无应力安装线形坐标来实现的,无应力安装线形在NLABS程序中以结果文件的形式保存,坐标的修改比较容易。
(3)合龙口两端梁段线形的相对位置调整。通过调整合龙口位置处斜拉索的方式可以对合龙口两端梁段的相对位置进行调整,使其满足基准状态下的要求,从而实现边跨和中跨合龙。完成合龙以后,再将调整过的斜拉索恢复到其调整前的状态。
(4)考察主梁制造参数变化对结构的响应,确定主梁制造参数变化对成桥线形和斜拉索索力的影响。
2 工程概述及计算模型 2.1 工程概述
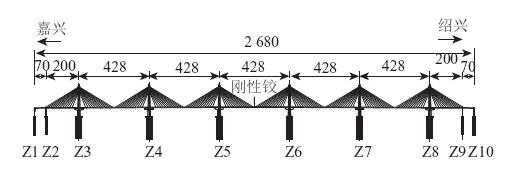
嘉绍大桥为四索面、六塔独柱式、分幅式钢箱梁斜拉桥,跨径布置为:70+200+5×428+200+70=2 680 m;索塔最大高度172.174 m,横桥面宽55.6 m(包括布索区),内侧梁高4.0 m,单幅梁宽24.0 m(包括风嘴区及检修区),双向八车道,嘉绍大桥主桥斜拉桥结构形式如图 1所示。
|
| 图 1 嘉绍跨江大桥结构图(单位:m) Fig. 1 Structure of Jiaxing-Shaoxing bridge(unit: m) |
基于西南交通大学桥梁工程系研发的大跨径桥梁结构专用计算分析系统软件NLABS,建立了嘉绍大桥的有限元结构模型,该分析系统软件可以考虑几何非线性特性,图 2所示为其有限元结构离散图。

|
| 图 2 嘉绍跨江公路大桥结构离散图 Fig. 2 Structural scattergram of Jiaxing-Shaoxing highway bridge |
嘉绍大桥采用基于几何控制的全过程控制方法,加强了厂内制造控制的重点,主梁控制的内容为:钢箱梁梁重、节段梁长以及节段间夹角等。本节就主梁控制的主要内容,根据厂内获得的实测数据对钢箱梁梁重、节段梁长及节段间夹角误差进行统计,获得主梁关键制造参数的误差范围,从而确定参数敏感性分析时的参数变化值。
(1)主梁钢箱梁节段自重的误差统计
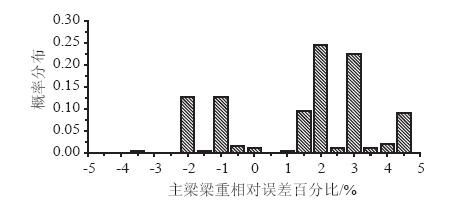
对嘉绍跨江大桥部分主梁钢箱梁节段进行自重统计,共统计的节段钢箱梁有168块(共有374块),主梁节段自重的相对误差概率分布图如图 3所示。
|
| 图 3 主梁钢箱梁节段自重误差概率分布 Fig. 3 Probability distribution of girder steel box segment weight errors |
由图 3可得,主梁节段自重相对误差区间在[-4,+4)的概率可达0.909,因此取主梁节段自重相对误差值为±4%时,分析主梁自重参数变化对成桥状态的影响。
(2)主梁钢箱梁节段梁长的误差统计
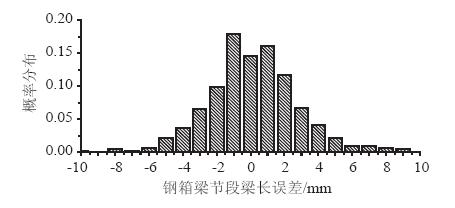
将嘉绍大桥所有节段梁长进行统计,主梁节段梁长的误差概率分布图如图 4所示。
|
| 图 4 主梁钢箱梁节段梁长误差概率分布 Fig. 4 Probability distribution of girder steel box segment length errors |
由图 4可得,主梁节段梁长误差区间在[-4,+4)的概率可达0.910,因此取主梁钢箱梁节段梁长误差值为±4 mm时,分析主梁节段梁长参数变化对成桥状态的影响。
(3)主梁钢箱梁节段间制造夹角的误差统计
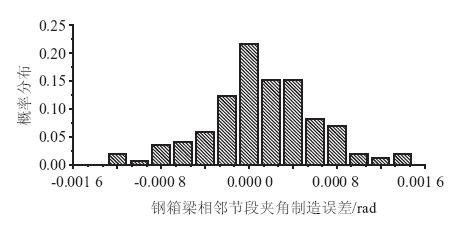
将嘉绍大桥所有主梁节段间制造夹角的误差进行统计,主梁钢箱梁节段间夹角的制造误差概率分布图如图 5所示。
由图 5可得,主梁节段间制造夹角误差区间在[-0.000 8,+0.000 8)的概率可达0.930,由于主梁节段间制造夹角的改变可以通过调整顶底板的焊缝宽度差来实现,经换算可得制造夹角变化±0.000 8 rad时,顶底板焊缝宽度的差值为±3 mm,因此取主梁钢箱梁底板制造长度误差值为±3 mm时,分析主梁制造夹角参数变化对成桥状态的影响。
|
| 图 5 主梁钢箱梁节段间制造夹角误差概率分布 Fig. 5 Probability distribution of steel box segment fabrication angle errors |
本研究针对主梁制造过程中关键制造参数的变化,进行系统全面的基于几何控制法的施工全过程单参数敏感度分析。嘉绍大桥为六塔斜拉桥,主塔编号为Z3~Z8,仅变化Z4塔主梁制造参数,这样不仅可以考察结构对主梁关键制造参数的敏感性,同时可以揭示多塔斜拉桥各塔间主梁制造参数变化引起的相互影响。由于篇幅有限,仅列出主梁制造参数变化对主梁成桥状态几何线形和斜拉索成桥索力的影响。
4.1 合龙前线形及调整
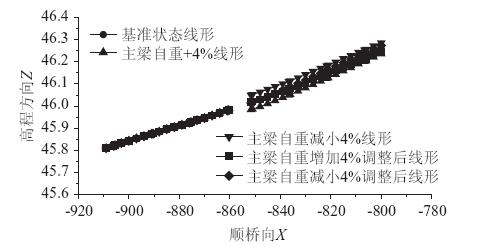
合龙前合龙口线形的调整是几何控制法的关键性施工工况之一,也是保证最终成桥状态接近目标成桥状态的前提条件[12]。本节以自重参数变化为例,当主梁自重发生变化时,合龙口合龙前线形及调整后线形如图 6所示:
|
| 图 6 主梁自重变化对最大悬臂状态合龙口线形的影响(单位:m) Fig. 6 Impact of variation of girder weight on closure geometric shape in the largest cantilever state(unit:m) |
由图 6可知,当主梁节段自重变化值为±4%时,处于大悬臂的施工状态时,主梁边、中跨两侧悬臂段几何线形的最大变化量分别为-33.1 mm和33.2 mm。分别调整最大悬臂端附近11#,12#索的无应力索长,调整后主梁线形基本满足设计状态下的要求。
4.2 主梁制造参数敏感性分析结果
(1)主梁自重参数敏感性分析
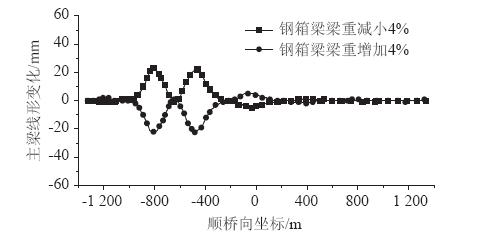
当主梁钢箱梁自重参数变化±4%时,在成桥状态下主梁几何线形和斜拉索索力影响如图 7和图 8所示。
|
| 图 7 主梁钢箱梁自重变化对成桥线形的影响 Fig. 7 Impact of variation of girder weight on bridge geometric shape |
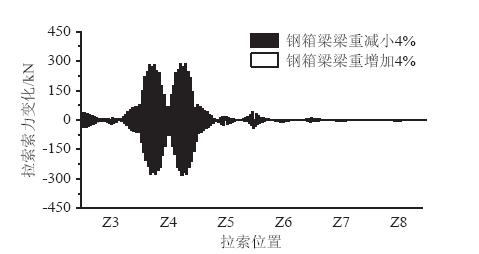
|
| 图 8 主梁钢箱梁自重变化对斜拉索索力的影响 Fig. 8 Impact of variation of girder steel box weight on cable force |
由图 7和图 8可以看出,主梁自重对较短悬臂斜拉桥主梁成桥几何线形有一定程度影响,主梁悬臂长度越大,结构刚度越小,主梁自重对主梁线形影响越明显,尤其长悬臂位置处主梁自重变化对主梁线形的影响程度越明显[13]。因此,当斜拉桥主梁悬臂长度较小时,结构自重变化对成桥几何线形的影响相对较小;同时可知,当Z4塔主梁自重变化时,不仅对Z4塔主梁成桥几何线形有影响,而且对相邻各塔主梁几何线形均有一定影响,且离Z4塔越远影响越小;斜拉索索力的相对变化量最大值为3.6%,最大值在跨中位置,且对相邻各塔斜拉索索力均有不同程度的影响。
(2)主梁节段梁长参数敏感性分析
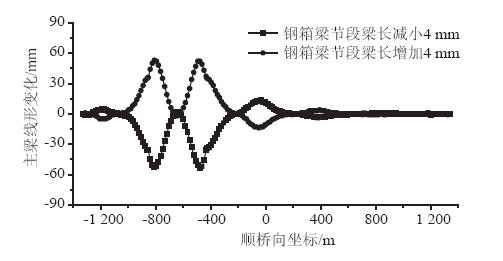
当主梁节段梁长参数变化±4 mm时,在成桥状态下主梁几何线形和斜拉索索力影响如图 9和图 10所示。
|
| 图 9 主梁钢箱梁节段梁长变化对成桥线形的影响 Fig. 9 Impact of variation of girder steel box segment length on bridge geometric shape |
|
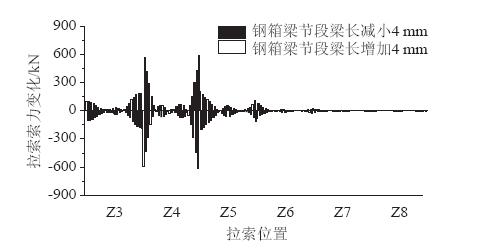
| 图 10 主梁钢箱梁节段梁长变化对斜拉索索力的影响 Fig. 10 Impact of variation of girder steel box segment on cable force |
由图 9和图 10可以看出,主梁节段梁长对斜拉桥主梁成桥几何线形有一定影响,主梁节段梁长变化会改变梁上锚点位置,且随着梁段的增加,节段梁长误差累积越明显,对后续梁段的锚点位置影响更为显著。当采取拉索无应力长度不变的控制张拉方式进行张拉时,保证斜拉索的无应力长度为基准条件下的长度值,同时保证其余结构参数均不发生改变,则拉索有应力长度的变化和锚点位置的改变是紧密相关的;若有应力索长产生较大改变时,此时会对成桥状态下的几何线形及拉索索力有较为显著的影响。因此,节段梁长变化对主梁成桥几何线形的影响较大;同时可以看出,当Z4塔主梁节段梁长变化时,不仅对Z4塔主梁成桥几何线形有明显影响,而且对相邻各塔主梁几何线形均有一定影响,且离Z4塔越远影响越小;斜拉索索力相对变化量的最大值为5.0%,最大值位于跨中位置,且对相邻各塔斜拉索索力均有不同程度的影响。
(3)主梁节段间夹角参数敏感性分析
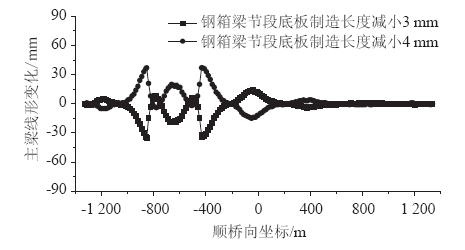
当主梁底板制造长度值变化±3 mm时,对主梁成桥几何线形和斜拉索索力的影响如图 11和图 12所示。
|
| 图 11 主梁钢箱梁节段夹角变化对几何线形的影响 Fig. 11 Impact of variation of girder steel box segment angle on geometric shape |
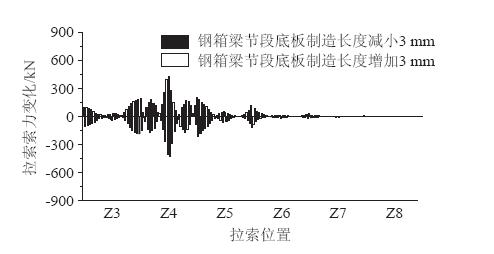
|
| 图 12 主梁钢箱梁节段夹角变化对斜拉索索力的影响 Fig. 12 Impact of variation of girder steel box segment angle on cable force |
由图 11和图 12可以看出,主梁节段间夹角对斜拉桥主梁成桥几何线形有一定影响,主梁节段间制造夹角发生变化时,斜拉索梁上锚固点位置将在安装匹配阶段发生变化,但以斜拉索索长为张拉控制的几何控制法,在张拉控制阶段会通过索长不变的方式进行自适应调节,使得制造夹角误差对该安装梁段的线形误差有所减小,且已成梁段线形误差将会随着后续梁段的施工逐渐减小[14],因此,主梁节段间制造夹角对主梁成桥几何线形影响相对较小;同时可知,当Z4塔主梁节段间夹角变化时,不仅对Z4塔主梁成桥几何线形有影响,而且对相邻各塔主梁几何线形均有一定影响,且离Z4塔越远影响越小;斜拉索的索力误差变化规律与主梁成桥线形误差变化规律是相对应的,斜拉索索力的相对变化量最大值为8.3%,最大值在短悬臂位置,且对相邻各塔斜拉索索力均有不同程度的影响。
(4)主梁制造参数敏感性分析结果汇总
当主梁制造参数发生变化时,进行几何控制法单参数敏感度分析计算,获得参数变化对成桥结构几何线形、塔偏位移、主梁应力、索塔应力和拉索索力的影响,其分析结果见表 1,表中结构应力以压为正。“+”表示索塔位移偏向江侧,“-”表示偏向岸侧。
| 结构参数变化 | 索塔应力/MPa | 主梁应力/MPa | 主梁成桥线形变化/mm | 拉索索力/kN | 塔偏/mm | ||
| 岸侧翼缘 | 江侧翼缘 | 上翼缘 | 下翼缘 | ||||
| 主梁自重+4% | -0.06~0.10 | -0.10~0.07 | -1.82~2.73 | -3.60~3.23 | -22~5 | -29.8~282.9 | -2.5~3.8 |
| 主梁自重-4% | -0.09~0.06 | -0.07~0.08 | -2.66~1.84 | -3.25~3.40 | -5~23 | -279.5~27.8 | -3.5~2.4 |
| 主梁制造长度增加4 mm | -0.26~0.17 | -0.20~0.24 | -6.34~3.93 | -3.71~9.40 | -14~53 | -202.8~588.1 | -10.1~6.9 |
| 主梁制造长度减小4 mm | -0.17~0.27 | -0.24~0.29 | -3.92~6.30 | -9.38~3.69 | -54~14 | -612.6~204.3 | -7.0~10.1 |
| 底板制造长度增加3 mm | -0.28~0.17 | -0.20~0.26 | -26.45~1.3 | -1.7~35.52 | -14~35 | -492.8~178.0 | -10.6~7.0 |
| 底板制造长度减小3 mm | -0.16~0.26 | -0.24~0.18 | -1.2~26.57 | -35.58~1.6 | -37~15 | -177.2~426.6 | -6.6~10.1 |
由表 1可知,在成桥状态下,主梁制造长度对主梁成桥线形和斜拉索索力影响较大,且对主梁和索塔应力有一定影响;主梁自重和主梁制造夹角对主梁成桥线形和斜拉索索力有一定影响,且主梁制造夹角对主梁应力影响较明显。综上所述,主梁自重、主梁制造长度及主梁制造夹角均对结构成桥状态有较大影响,应将主梁关键制造参数作为施工控制的重点。
4.3 工程实践
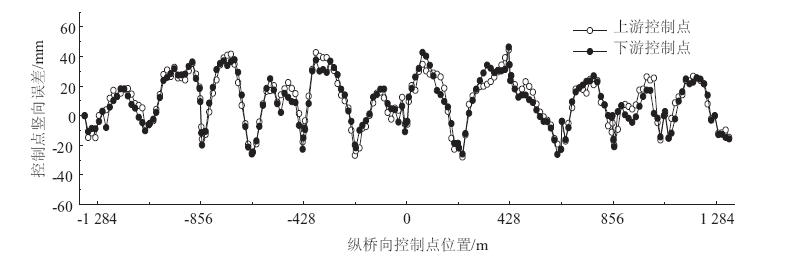
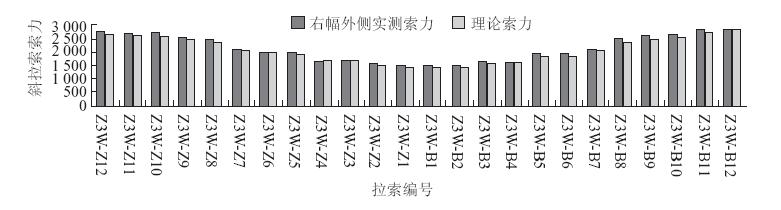
成桥二期恒载完成阶段,主梁成桥状态理论线形与实测线形对比如图 13所示;斜拉索成桥状态理论索力与实测索力对比如图 14所示。由于篇幅有限,仅列出上游幅成桥线形和Z3塔成桥索力结果。
|
| 图 13 上游幅主梁成桥实测线形与理论线形对比图 Fig. 13 Comparison of geometric shape of bridge upstream girder between measured values and theoretical values |
|
| 图 14 Z3塔右幅外侧斜拉索实测索力与理论索力对比图(单位:kN) Fig. 14 Comparison of cable force of right lateral cables of Z3 pylon between measured values and theoretical values (unit: kN) |
由主梁成桥实测线形与理论线形对比图 13可知,边跨70 m梁段标高误差最大值为23 mm,小于25 mm的限值;边跨200 m跨梁段标高误差最大值为49 mm,小于50 mm的限值;其余各跨梁段的标高误差最大值为60 mm小于100 mm的限值,主梁成桥线形均符合《嘉绍桥专用规范》的要求。
由斜拉索成桥实测索力与理论索力对比图可知,最大索力误差为4.5%,最大值位于Z4N-B1-L索,不超过5%的限值,满足嘉绍桥专用规范的要求,且斜拉索索力均具有足够的安全系数,斜拉索处于安全工作状态。
5 结论
根据主梁关键制造参数的敏感性分析结果可以得到以下结论:
(1)主梁钢箱梁自重对主梁成桥几何线形和斜拉索索力具有一定影响,在悬臂斜拉桥施工控制中,主梁自重变化对成桥线形的影响随悬臂长度的增加而增加,且长悬臂位置处主梁自重变化对主梁线形的影响程度越明显,因此,对于小跨径斜拉桥来说,主梁自重可以作为次要结构参数,而在大跨度斜拉桥中,主梁自重参数变化属于主要结构参数。
(2)主梁钢箱梁节段梁长对主梁成桥几何线形和斜拉索索力影响较大,因此在悬臂斜拉桥施工控制中主梁节段梁长变化为主要结构参数。
(3)主梁钢箱梁节段间制造夹角对主梁成桥几何线形和斜拉索索力影响相对较小,但对主梁和索塔的应力影响较大,因此在悬臂斜拉桥施工控制中主梁节段间制造夹角变化也应作为主要结构参数。
(4)在多塔斜拉桥制造阶段主梁关键参数敏感性分析中,当其中某塔主梁关键参数发生变化时,不仅对该塔主梁成桥几何线形和斜拉索索力有影响,而且对相邻各塔主梁几何线形和斜拉索索力均有一定程度的影响,且离该塔越远影响将逐渐减小。
(5)由工程实践可知,主梁成桥线形与斜拉索成桥索力误差均控制在限值要求范围以内,获得了良好的工程实践效果,因此,基于几何控制法的斜拉桥施工控制具有良好的施工控制精度。
| [1] | 翟世鸿,张照霞.国内超大跨度钢斜拉桥上部结构施工控制探讨[J].中外公路,2006,26(1):108-112.ZHAI Shi-hong,ZHANG Zhao-xia. Discussion of Construction Control of Upper Structure of Domestic Super-span Steel Cable-stayed Bridge[J].Journal of China & Foreign Highway,2006,26(1):108-112. |
| [2] | 石雪飞,项海帆. 斜拉桥施工控制方法的分类分析[J]. 同济大学学报:自然科学版,2001,29(1):55-59.SHI Xue-fei,XIANG Hai-fan. Analysis of Construction Control Systems of Cable-stayed Bridge[J].Journal of Tongji University:Natural Science Edition,2001,29(1):55-59. |
| [3] | TURANYI T. Sensitivity Analysis of Complex Kinetic System Tools and Applications [J].Journal of Mathematical Chemistry,1990,15(3):203-248. |
| [4] | 苏成,范学明.斜拉桥施工控制参数灵敏度与可靠度分析 [J].土木工程学报,2005,38(10):81-87.SU Cheng,FAN Xue-ming. Parameter Sensitivity and Reliability Analysis for Construction Control of Cable stayed Bridges[J]. China Civil Engineering Journal,2005,38(10):81-87. |
| [5] | 黄灿,赵雷,张清华. 特大跨度斜拉桥制造阶段参数敏感性分析及工程应用[J].四川建筑科学研究,2011,37(3):297-300.HUANG Can,ZHAO Lei,ZHANG Qing-hua. Sensitivity Analysis of Parameters of the Manufacturing Stage for Super-span Cable-stayed Bridge and Its Application [J].Sichuan Building Science,2011,37(3):297-300. |
| [6] | 黄灿,赵雷,卜一之. 特大跨度斜拉桥几何控制法单参数敏感性分析[J].公路交通科技,2012,29(5):70-75.HUANG Can,ZHAO Lei,BU Yi-zhi. Sensitivity Analysis of Single-parameters for Super-span Cable-stayed Bridge Based on Geometry Control Method[J]. Journal of Highway and Transportation Research and Development,2012,29 (5):70-75. |
| [7] | 卜一之,谢明志,张克跃,等.无应力索长误差对千米级混合梁斜拉桥影响分析分析[J].公路交通科技,2013,30(8):96-101.BU Yi-zhi,XIE Ming-zhi,ZHANG Ke-yue,et al. Influence of Error of Unstressed Cable Length on Mechanical Behavior of Thousand-meter Scale Hybrid Girder Cable-stayed Bridge[J].Journal of Highway and Transportation Research and Development,2013,30(8):96-101. |
| [8] | KAMRUNNAHAR M,BRAATZ R D,ALKIRE R C. Parameter Sensitivity Analysis of Pit Initiation at Single Sulfide Inclusions in Stainless Steel [J]. |
| [9] | LÜDTKE N, PANZERI S,BROWN M,et al. Information-theoretic Sensitivity Analysis:A General Method for Credit Assignment in Complex Networks[J]. |
| [10] | 李建慧,李爱群,郭彤. 斜拉桥不确定性参数随机分析研究[J]. 公路交通科技,2008,25(11):72-77.LI Jian-hui,LI Ai-qun,GUO Tong. Stochastic Analysis and Research of Parameter Uncertainty of Cable-stayed Bridge[J].Journal of Highway and Transportation Research and Development,2008,25(11):72-77. |
| [11] | 李乔,卜一之,张清华. 大跨度斜拉桥施工全过程几何控制概论与应用[M].成都:西南交通大学出版社,2009.LI Qiao,BU Yi-zhi,ZHANG Qing-hua. Conspectus of the Geometry Control Method of the Whole-procedure of Long-span Cable-stayed Bridge and Application [M].Chengdu:Southwest Jiaotong University Press,2009. |
| [12] | 黄灿,卜一之,张清华. 特大跨度斜拉桥施工几何控制原理的数值验证[J].中国工程科学,2009,11(1):87-91.HUANG Can,BU Yi-zhi,ZHANG Qing-hua. Numerical Verification of Geometry Control Theory of the Construction for Super-span Cable-stayed Bridge [J]. Engineering Science,2009,11(1):87-91. |
| [13] | 王学伟. 基于几何控制法的六塔斜拉桥制造控制应用研究[D].成都:西南交通大学,2013.WANG Xue-wei. Fabrication Control Application Research of Six-pylon Cable-stayed Bridge Based on Geometry Control Method [D]. Chengdu: Southwest Jiaotong University,2013. |
| [14] | 黄灿.基于几何控制法的大跨度斜拉桥自适应施工控制体系研究[D].成都:西南交通大学,2011.HUANG Can. Adaptive Construction Control System of Super-span Cable-stayed Bridge Based on Geometry Control Method [D]. Chengdu:Southwest Jiaotong University,2011. |
 2015, Vol. 31
2015, Vol. 31
