扩展功能
文章信息
- 刘建, 桂勋, 李传习
- LIU Jian, GUI Xun, LI Chuan-xi
- 基于健康监测的自锚式悬索桥钢箱梁细节疲劳可靠度研究
- Study on Fatigue Reliability of Details of Steel Box Girders of a Self-anchored Suspension Bridge Based on Health Monitoring
- 公路交通科技, 2015, Vol. 31 (1): 69-75
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 69-75
- 10.3969/j.issn.1002-0268.2015.01.012
-
文章历史
- 收稿日期:2014-01-07
2. 长沙理工大学, 湖南 长沙 410114
2. Changsha University of Science and Technology, Changsha Hunan 410114, China
随着桥梁使用时间的增加、交通荷载的增大和环境因素的耦合作用等,桥梁结构的抗力逐渐退化,甚至发生灾难性事故,其中钢桥的疲劳损伤是事发原因之一。位于美国俄亥俄州的The Silver Bridge发生了由于两条腐蚀疲劳裂纹导致整桥垮塌的事件。在超负荷车辆荷载与环境腐蚀作用共同作用下,桥梁构件的损伤速度远远大于预期设计值,从而导致桥梁使用时间未到其设计基准期就发生破坏。因此,作为国内最大跨度的独塔自锚式悬索桥,平胜大桥钢箱梁构造细节的疲劳性能值得研究。
疲劳破坏的内因是钢材的局部应力集中,外因是应力幅值和循环次数,其中裂纹的萌生和扩展过程决定了钢材的疲劳性能[1]。钢箱梁的疲劳性能具有变幅、高循环和低应力等特点,采用常规的Palmgren-Miner方法无法解决此类问题。Miner[2]在试验研究的基础上提出了等效疲劳幅值的方法。考虑到结构参数和外部荷载的随机性,基于确定性疲劳的计算理论难以解决既有钢箱梁的随机疲劳问题,然而疲劳可靠度可以真实反映疲劳的随机累积和演化过程[3]。目前针对疲劳可靠度的研究方法有两类:一是基于S-N曲线和线性损伤累积理论的方法,二是基于线弹性断裂力学方法[4, 5]。
钢箱梁桥疲劳可靠度研究的基础是获取疲劳应力谱,传统的应力谱分析方法大多是根据现场调查和规范选取的结果,模拟不同类型车辆通过时的应力谱[6]。然而由于实际车辆荷载与统计和规范值有所差异,加之有限元模型与实际桥梁的差异,因此传统的应力谱方法并不能真实反映出桥梁在运营期的疲劳状态。桥梁健康监测系统的发展为上述问题的解决提供了有利条件。健康监测系统能够采集到桥梁在运营期随机应力过程的真实数据,再转换为应力谱,即可实现既有桥梁的疲劳可靠度评估[7]。
本文以独塔自锚式悬索桥平胜大桥为工程背景,在健康监测应力数据的基础上采用疲劳可靠度理论对其钢箱梁桥面板构造细节疲劳性能及疲劳可靠度进行了研究,最后分析了交通量增长系数对疲劳可靠度的影响。
1 疲劳可靠度分析模型 1.1 疲劳可靠度的极限状态方程
结构疲劳可靠度的分析方法有线性累积损伤方法和线弹性断裂力学方法。本文基于Palmegren-Miner线性累积损伤法则和S-N曲线对钢箱梁结构进行疲劳可靠度分析。线性累积损伤理论认为,总疲劳损伤是由变幅应力循环Si所造成疲劳操作的线性叠加,总损伤可表示为[8]:
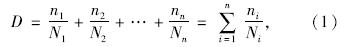
Miner提出的S-N曲线方程反映了外加应力和疲劳寿命的关系,该曲线方程表示为:

通过式(1)和式(2)可以分析确定结构的疲劳问题,然而在随机车辆荷载作用下,钢箱梁的疲劳破坏是结构随机损伤的累积过程,其功能函数可表示为:
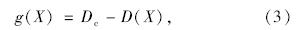
S-N曲线方程和线性累积损伤法则可得到累积损伤的表达式:
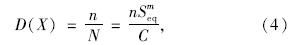
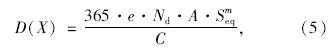
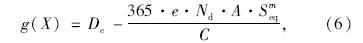
文献[12]采用Monte-Carlo(MC)方法分析了斜拉桥拉索的疲劳可靠度。然而当疲劳失效概率较低时,该方法需要大量的抽样次数,以致计算机无法完成。因此本文选取JCSS推荐的一次二阶矩法(FOSM)方法进行可靠度分析。
由于表 1所示随机变量多为非正态分布,因此应引入R-F当量正态变换准则[13],将表 1所示非正态分布参数在验算点处当量正态化为正态分布参数。对于对数正态分布的当量正态化公式为:
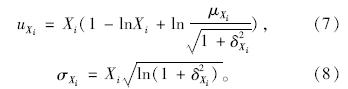
文献[14]给出了基于MATLAB语言的FOSM算法的流程与程序。
2 基于健康监测数据的疲劳应力分析 2.1 平胜大桥的健康监测系统
佛山平胜大桥[15]是目前世界上最大跨度的独塔自锚式悬索桥。其总体布置为39.64 m+5×40 m+30 m(混凝土加劲梁及锚跨)+350 m(钢加劲梁)+30 m+29.60 m(混凝土锚跨),主桥全长680.20 m(含两端的伸缩缝宽),主塔承台以上结构高度为138.87 m。设计时速100 km/h,设计车辆荷载为:汽车——超20级,挂车——120,一级公路,城市A级验算。主要对主梁截面进行应力监测,全桥共测试7个断面,每个断面(左右两幅)共安装10个光纤光栅应变传感器,具体布置截面及位置如图 1所示。

|
| 图 1 平胜大桥全桥应变传感器布置图 Fig. 1 Arrangement of strain sensors on Pingsheng bridge (unit: m) |
由健康监测系统得出应力时程后,需要将原始应力转换为应力循环。采用文献[16]提出的雨流计数法可将应力时程数据转换为应力-应变滞回曲线,即可用于疲劳累积损伤分析。图 2给出了采用雨流计数法基本原理得出的应力循环为1-4-7,2-3-2′,5-6-5′。

|
| 图 2 雨流计数法的基本原理 Fig. 2 Fundamental of rainflow counting method |
由图 2可知组成应力循环的元素是应力时程的峰谷点,而曲线中非拐点不会对疲劳损伤产生影响,因此,在雨流计数之前可以对数据进行预处理。本文采用三点比较法提取应力峰谷。提取步骤为:首先从原始数据中依次读取应力数据,然后依次对比应力值大小,若某个数据为极大值或极小值,则保留数据,并删除其余数据,最后将极大值和极小值依次连接。该方法处理的某50组应力数据如图 3、图 4所示。

|
| 图 3 原始应力时程曲线 Fig. 3 Original stress time-history curve |

|
| 图 4 谷峰方法处理后的应力时程曲线 Fig. 4 Processed stress time-history curve using valley-peak method |
经过峰谷处理后的数据得到了大幅的压缩,节省了雨流计数的时间,同时也避免了由于健康监测系统中采样频率过高造成的循环数据失真的影响。
2.3 疲劳应力统计分析
文献[9]对润扬长江大桥钢箱梁板面板的疲劳可靠度研究结果表明,在车辆荷载作用下钢箱梁的顶板-U肋处的疲劳可靠度较低。因此,本文选取主梁跨中截面在顶板-U肋处的数据进行处理。
平胜大桥健康监测系统在2012年2月13日统计编号为BCV-5-7处的光纤光栅传感器的应力数据和编号为RT-5-1的温度传感器的温度时程数据,该数据为典型的温度及应力时程数据,其中温度时程数据如图 5所示。为了排除温度变化对应力时程的影响,采用小波分析方法提出应力时程的低频成份,此成份即为温度变化引起的应力变化数据。然后将此低频成份删除,即得到车辆荷载作用下钢箱梁的应力时程曲线。此时即可按图 4所示的谷峰方法和雨流计数提取应力循环。

|
| 图 5 2012年2月13日采集的编号为RT-5-1的温度时程图 Fig. 5 Temperature time-history of No. RT-5-1,2012-02-13 |
由图 6可以看出,采集的疲劳应力幅值为低应力幅值。中国铁路TB99规范没有给出低应力幅值和构造细节对疲劳的影响,而BS500规范、AASHTO规范和Erucode规范[17]均对低应力幅值和构造细节给出了相应的处理方法。本文选取Eurocode规范处理对疲劳细节和疲劳应力的分类。针对本文正交异性板的构造特征,根据EC3规范要求,相应的细节类型为50,常幅应力极限为ΔσD=37 MPa,应力截止限为ΔσL=20 MPa。由图 6可看出,疲劳应力谱的大部分应力均小于常幅疲劳极限ΔσD,即Seq<ΔσD。根据疲劳损伤等价原则,将变幅应力循环等效为常幅应力循环,则等效常幅应力为:
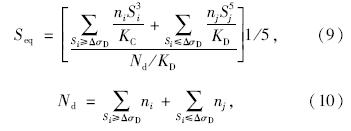

|
| 图 6 2012年2月13日采集的编号为BVC-5-7的应力循环图 Fig. 6 Stress-cycle curve of No.BVC-5-7,2012-02-13 |
式中,Si和ni分别为应力谱中大于常幅疲劳极限ΔσD的应力和对应的循环次数;Sj和nj分别为应力谱中小于ΔσD的应力和对应的循环次数;KC和KD分别为应力幅大于和小于ΔσD的疲劳强度系数。针对于本文正交异性板的构造特征,细节类型为50所对应的KC和KD分别为2.5×1011和1.9×1015;Nd为单日循环总次数,在本文中的Nd已经排除应力幅值小于20 MPa 的应力循环。
由式(9)、(10)得出单日等效应力幅Seq和应力循环次数Nd后,即可按此方法得到2012年统计的300组Seq和Nd数据。然后采用K-S检验获取Seq和Nd的概率分布类型和分布特征值,其概率分布与拟合图如图 7、图 8所示。由于平胜大桥主梁为分幅式钢加劲梁,为使选择测点具有代表意义,现将中跨跨中位置和1/4位置的应力数据进行统计分析,其中每个位置均取上下游两个测点,统计特征值如表 2所示,其中各点的损伤值由式(4)计算出。

|
| 图 7 等效应力幅值的概率分布 Fig. 7 Probability distribution of equal stress amplitudes |

|
| 图 8 日循环次数的概率分布 Fig. 8 Probability distribution of daily cycles |
由表 2可知,中跨跨中BVC-5-2传感器所在位置的疲劳损伤最大,因此本文下述内容选取BVC-5-2处的构造位置进行疲劳可靠度分析。
| 荷载效应 | 跨中 | 1/4跨 | ||||||
| 上游BVC-5-2 | 下游BVC-5-7 | 上游BVC-4-2 | 下游BVC-4-7 | |||||
| Seq | Nd | Seq | Nd | Seq | Nd | Seq | Nd | |
| 均值μ | 5.31 | 3 214 | 5.24 | 3 167 | -5.31 | 3 214 | -5.31 | 3 214 |
| 标准差σ | 1.58 | 861 | 7.58 | 823 | 7.58 | 513 | 7.58 | 513 |
| 均值μ的日损伤值 | 1.30×10-6 | 1.23×10-6 | 4.29×10-7 | 3.94×10-7 | ||||
综合以上内容,本文采用的疲劳可靠度分析流程如图 9所示。该分析方法分为两个过程:疲劳应力分析过程和疲劳可靠度与寿命预测过程。值得说明的是,根据线性疲劳损伤原理和Eurocode规定[17]在计算等效疲劳荷载时,将应力循环数据分为3类。第1类应力幅值为σi>37 MPa,该类应力的疲劳S-N曲线的m值为3;第2类应力幅值为20 MPa<σi<37 MPa,该类应力m值为5;第3类应力幅值为σi<20 MPa,该类应力幅值不计入应力损伤。
根据图 9所示流程图,可以计算出测点号为BVC-5-2在2012年的疲劳可靠指标为β=5.274。采用FORM的迭代过程如图 10所示。

|
| 图 9 疲劳可靠度分析的流程图 Fig. 9 Flowchart of fatigue reliability analysis |

|
| 图 10 可靠指标迭代过程 Fig. 10 Iterative process of reliability indicator |
考虑循环次数Nd随着服役年限呈线性增长趋势,并定义a为线性增长系数,则由式(6)所示的功能函数可得到第A年疲劳可靠度的功能函数为:
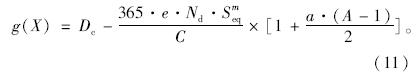
由此可得出当交通量线性增长系数分别为0,0.1和0.2时,跨中位置BVC-5-2测点在100 a内的疲劳可靠指标,计算结果如图 11所示。

|
| 图 11 交通量增长系数a和服役时间T对疲劳可靠指标的影响 Fig. 11 Influence of traffic volume growth factor a and service time T on fatigue reliability indicator |
由图 11可以看出:若不考虑交通量增长系数,则疲劳可靠指标由初始的5.274,到100 a后下降至2.305,在0~80 a期间可靠指标呈直线下降趋势,而在80~100 a期间可靠指标呈平缓下降趋势;在取交通量增长系数a=0.1时,100 a后的疲劳可靠指标下降为1.681,下降趋势与不考虑交通量增长时相同;在取交通量增长系数为a=0.2时,100 a后的疲劳可靠指标下降为1.395。
4 结论
本文基于平胜大桥健康监测的典型应力及温度数据对钢箱梁的细节疲劳可靠度进行了研究,建立了疲劳可靠度的功能函数,采用雨流计数法和谷峰方法处理并提取应力循环,并以Eurcode规范将变幅应力幅值进行等效处理,最后对考虑不同交通量增长系数和不同服役时间的疲劳可靠度进行分析。主要得出以下结论:
(1) 基于健康监测数据可及时更新疲劳可靠性分析的数据库,给出疲劳细节的概率统计特征,同时根据交通量的情况预测桥梁的寿命周期,这对桥梁的安全运营及检修加固有重要的意义。
(2) 平胜大桥钢箱梁细节疲劳应力数据具有低应力幅值和高循环的特点,基于Erucode规范对构造细节和低应力幅值的处理方法,通过等效损伤可得出等效应力幅值。
(3) 不考虑交通量增长时,平胜大桥钢箱梁细节疲劳可靠指标在2012年为5.274,100 a后下降为2.305。
(4) 交通量增长系数分别为0.1和0.2时,平胜大桥钢箱梁细节疲劳可靠指标在100 a后分别下降为1.681和 1.395。交通量增长系数在前期对疲劳可靠指标的影响较小,而后期对疲劳可靠指标的影响较大。
| [1] | 郭彤,李爱群. 基于长期监测数据的桥面板焊接细节疲劳寿命评估[J]. 土木工程学报,2009 (6): 66-72.GUO Tong,LI Ai-qun. Fatigue Life Assessment of Welds in Bridge Decks Using Long Term Monitored Data[J] China Civil Engineering Journal,2009 (6): 66-72. |
| [2] | MINER M A. Cumulative Damage in Fatigue[J]. Journal of Applied Mechanics,1945,12(3): 159-164. |
| [3] | CHEUNG M S,LI W C. Probabilistic Fatigue and Fracture Analyses of Steel Bridges[J]. |
| [4] | LIU M,FRANGOPOL D M,KWON K. Fatigue Reliability Assessment of Retrofitted Steel Bridges Integrating Monitored Data[J]. |
| [5] | 邓扬,丁幼亮,李爱群,等. 钢箱梁桥焊接细节的疲劳断裂可靠性分析[J]. 工程力学,2012,29(10): 122-128.DENG Yang,DING You-liang,LI Ai-qun,et al. Fracture Fatigue Reliability of Welded Details in Bridge Steel Box Girders[J] Engineering Mechanicals,2012,29(10): 122-128. |
| [6] | GUO T,FRANGOPOL D M,CHEN Y. Fatigue Reliability Assessment of Steel Bridge Details Integrating Weigh-in-motion Data and Probabilistic Finite Element Analysis[J]. Computers & Structures,2012,112: 245-257. |
| [7] | KWON K,FRANGOPOL D M. Bridge Fatigue Reliability Assessment using Probability Density Functions of Equivalent Stress Range based on Field Monitoring Data[J]. |
| [8] | 贡金鑫,王海超,赵国藩. 结构疲劳累积损伤与极限承载能力可靠度[J]. 大连理工大学学报,2002,42(6): 714-718.GONG Jin-xin,WANG Hai-chao,ZHAO Guo-fan. Ultimate Bearing Capacity Reliability of Structures Subjected to Accumulated Fatigue Damage[J]. Journal of Dalian University of Technology,2002,42(6): 714-718. |
| [9] | 邓扬,丁幼亮,李爱群. 钢箱梁焊接细节基于长期监测数据的疲劳可靠性评估: 疲劳可靠度指标[J]. 土木工程学报,2012,45(3): 86-92.DENG Yang,DING You-liang,LI Ai-qun. Fatigue Reliability Assessment for Welded Details of Steel Box Girders Using Long-term Monitoring Data: Fatigue Reliability Indices[J]. Chinese Civil Engineering Journal,2012,45(3): 86-92. |
| [10] | ZHAO Zheng-wei,HALDAR A,BREEN F L,Jr. Fatigue-reliability Evaluation of Steel Bridges [J]. |
| [11] | 李岩,吕大刚,盛洪飞. 考虑随机车载-风载联合作用的斜拉桥拉索疲劳可靠性分析[J]. 中国公路学报,2012,25(2): 60-66.LI Yan,LV Da-gang,SHENG Hong-fei. Fatigue Reliability Analysis on Cable of Cable-stayed Bridge Under Random Vehicle Load and Wind Load[J]. China Journal of Highway and Transport,2012,25(2): 60-66. |
| [12] | 杨美良,李波,张建仁. 车辆荷载作用下部分斜拉桥拉索疲劳可靠度研究[J]. 公路交通科技,2007,24(12): 66-68.YANG Mei-liang,LI Bo,ZHANG Jian-ren. Research on Fatigue Reliability of Cables of Paritally Cable-stayed Bridge under Vehicle Load[J]. Journal of Highway and Transportation Research and Development,2007,24(12): 66-68. |
| [13] | 蒋友宝,刘扬,张建仁. 具有非线性功能函数的结构时变可靠度分析[J]. 工程力学,2010 (1): 28-32.JIANG You-bao,LIU Yang,ZHANG Jian-ren.Time-dependent Reliability Analysis of Structures with Nonlinear Performance Function[J] Engineering Mechanics,2010 (1): 28-32. |
| [14] | 张明. 结构可靠度分析方法与程序[M]. 北京:科学出版社,2009: 148-153.ZHANG Ming. Structural Reliability Analysis Methods and Procedures[M]. Beijing: Science Press,2009: 148-153. |
| [15] | 佛山市路桥建设有限公司. 大跨径自锚式悬索桥-广东佛山平胜大桥[M].北京:人民出版社,2008.Foshan Road & Bridge Construction Co.,Ltd. Long-span Self-anchorage Suspension Bridge: Pingsheng Bridge in Foshan,Guangdong [M]. Beijing: China Communications Press,2008. |
| [16] | DOWNING S D,SOCIE D F. Simple Rainflow Counting Algorithms[J]. |
| [17] | BSEN1993-1-9:2005,Eurocode3: Design of Steel Structures,Part 1-9: Fatigue[S]. |
 2015, Vol. 31
2015, Vol. 31
