扩展功能
文章信息
- 李林峰
- LI Lin-feng
- 基于位移反分析的拓宽路基差异沉降预测
- Prediction of Differencial Settlement of Widened Subgrade Based on Displacement Back Analysis
- 公路交通科技, 2015, Vol. 31 (1): 57-62
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 57-62
- 10.3969/j.issn.1002-0268.2015.01.010
-
文章历史
- 收稿日期:2013-02-21
2. 福建省公路水运工程重点实验室, 福建 福州 350004
2. Fujian Key Laboratory of Highway and Water Transport, Fuzhou Fujian 350004, China
目前,高速公路拓宽工程中亟待解决的一大技术难题是软基差异沉降预测。这是因为对原有路堤进行拓宽,在拓宽路堤荷载作用下,地基力学行为和变形特性变得更为复杂。近年来,尽管对软土特性有了较为深入的了解,在软土地基沉降预测方面也做了许多细致的工作,提出了多种预测方法,主要归纳为两大类:(1)通过土工试验获得参数,选择合适的计算模型来计算沉降量,主要为有限元法、分层总和法;(2)根据沉降实测资料来推测最终沉降量,主要有曲线拟合法、灰色理论、BP神经网络法和遗传算法、反演分析法、支持相量机法等。但由于勘察、试验以及理论上存在的各种不确定因素,计算模型、预测模型的不够贴近实际,使预测结果与实测结果之间往往存在较大的差距,从而制约了沉降预测的工程应用[1, 2, 3, 4, 5]。
本文采用基于位移反分析的有限元预测方法在很大程度上可解决这一问题。它是一种计算模型较为简明、计算参数较少的计算方法。该方法利用现场测量数据作为位移反分析模型的输入信息,反演得到需要的材料参数,进而将反演获得的材料参数输入有限元计算模型中进行变形预测,克服了常规预测方法的局限性,可实现对公路拓宽工程新旧地基差异沉降进行预测。
1 位移反分析简介 1.1 位移反分析的基本思路
岩土工程反分析理论最早由Kavanagh K和Clough R于1972年在固体弹模反演有限元方法中提出后,经过众多国内外学者的不懈努力已逐步发展成熟起来,反分析方法有很多种[6]。本文通过神经网络和遗传算法相结合,提出一种用于位移反分析的进化神经网络方法,以解决传统的各种优化方法易于陷入局部最优值和映射关系难以确定的问题,使得改进后的遗传算法既有很好的全局寻优能力又有很强的局部寻优能力,并将改进后的遗传算法作为BP神经网络的学习算法形成进化神经网络。该进化神经网络方法既利用了神经网络的非线性映射、网络推理和预测功能,又利用了遗传算法全局优化特性,可处理变量与目标函数值之间无明显的数学表达式的复杂工程问题。同时在建立进化神经网络的训练样本时引入正交试验设计理论,减少了样本数量,可实现多参数同时反演,大大提高了反分析速度和准确性[6, 7, 8, 9]。
1.2 位移反分析方法的基本步骤
利用神经网络的非线性映射能力,建立起反演参数与目标函数值F(x)之间的映射关系,然后利用遗传算法对参数{x}m在约束条件下进行搜索、寻优,每搜索到一组参数{x}m便输入给已经训练好的网络,网络自动将其与学得的知识进行匹配,并推理、预测与之对应的目标函数值F(x),根据F(x)值的大小进行遗传变异操作,最后找到全局最优解[10]。具体步骤如下:
(1)选择位移反分析时段和反分析特征点;
(2)对材料参数进行敏感度分析,确定敏感度高的参数进行位移反分析;
(3)确定待反分析参数的取值范围,并依据正交试验设计理论,设计待反演的材料参数样本;
(4)建立有限元分析模型实现由材料参数到变形计算值的正分析过程,计算得到相应的变形值样本;
(5)建立进化神经网络将第③和第④步得到的参数样本和变形值样本作为网络的学习样本;
(6)训练进化神经网络;
(7)将实测变形值输入到训练好的进化神经网络,输出即为待反演的参数值;
(8)检验评价反分析结果。
2 有限元计算模型的建立 2.1 工程概况
沈海高速公路福厦漳段穿越闽东南沿海冲海积平原区,起于福州青口互通,止于漳州漳诏高速公路的东园,全长270 km。沿线软基主要由海积或冲海积相沉积物组成,地表覆盖第四纪松散堆积物,以黏粉粒为主,含少量中粗砂,下覆淤泥、淤泥质黏土、粉质黏土、砂质黏性土及砾石等。地下水埋藏较浅,雨季水量变化大。
原有高速公路泉厦段1997年建成通车,福泉段1999年建成通车。至今,该高速公路已经运营十余年,旧路地基和路堤变形已基本完成。扩建时,由于新旧地基边界条件、地基处理方式及两者经历的应力历史等均存在差异及新旧路堤相互作用的影响,公路拓宽工程中地基力学和变形特征更为复杂,若处理不当将会引起新旧路堤间过大的不均匀沉降。为此,为掌握新旧路基变形特性和沉降规律,指导施工,对旧路地表和拓宽路堤进行了沉降监测。其中,旧路地表采用水准仪加测微器进行沉降监测;在拓宽路堤中,通过在路堤施工初期预埋沉降管,采用剖面沉降仪进行了全断面沉降监测,为新旧路基差异沉降预测提供了宝贵的基础资料。
2.2 几何模型及其边界条件 2.2.1 几何模型
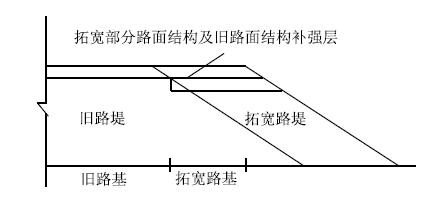
以YK307+750监测断面为例建立有限元模型,地基土从上到下分别为素填土1.4 m、淤泥质黏土2.7 m、粉质黏土4.8 m、残积砂质黏性土6.1 m。该监测断面路堤高度为3.58 m,路面厚度为 0.79 m,旧路堤宽26 m,两侧均拓宽8 m,坡比为1∶1.5,见图 1。软基采用CFG桩处理,桩间距为2.5 m,桩径为0.5 m,桩长为9.5 m。计算中取右半幅建立几何模型,单侧宽度为50 m。
|
| 图 1 拓宽路堤横断面示意图 Fig. 1 Schematic diagram of cross-section of idened embankment |
模型两侧边界水平向位移、底边边界水平和垂直向位移为零,原地面为排水边界,即孔隙水压力为零。计算中采用有效应力方法。
2.3 材料参数
计算中黏土层采用修正剑桥模型,其主要参数为初始孔隙比e0、压缩曲线斜率λ、临界状态线斜率M、泊松比μ、回弹曲线斜率κ、曲度常量β和屈服应力比K等,其余采用摩尔库伦弹塑性模型,通过对软土地基物理力学性质分析,并通过不同参数取值的有限元计算结果与实测结果比较,确定各参数取值,具体见表 1和表 2。为简化计算,对淤泥质黏土、粉质黏土、残积砂质黏性土层参数进行土层厚度加权平均,得到修正剑桥模型材料参数,旧地基中采用排水固结处理,相对于拓宽地基,渗透系数适当提高,一般取为拓宽地基的5~10倍,其余材料力学相同。CFG桩体模量为400 MPa,计算中采用地下连续墙等效替换,经换算后取为80 MPa。
| 土体类型 | 厚度/m | c/kPa | φ/(°) | E/MPa | μ | γ/(kN·m-3) |
| 路面层 | 0.79 | — | — | 825 | 0.25 | 24.0 |
| 路堤填土 | 3.08 | 20 | 25 | 35 | 0.30 | 20.0 |
| 级配碎石砂加褥垫层 | 0.50 | 0 | 34 | 200 | 0.30 | 22 |
| 素填土 | 1.40 | 42.4 | 20.4 | 4.94 | 0.30 | 19.3 |
| 淤泥质黏土 | 2.70 | 11.4 | 14.7 | 3.39 | 0.42 | 17.1 |
| 粉质黏土 | 4.80 | 8.0 | 8.7 | 3.93 | 0.35 | 18.6 |
| 残积砂质黏性土 | 6.10 | 23.2 | 19.3 | 4.24 | 0.30 | 18.3 |
| CFG桩 | — | — | — | 400 | 0.30 | 22 |
| 地基类型 | e0 | μ | M | λ | κ | β | K | Γ/(kN·m-3) | k/(×10-3·m·d-1) |
| 拓宽地基 | 0.95~1.15 | 0.34 | 0.37~0.77 | 0.1~0.2 | 0.03 | 0.8 | 0.9 | 18.2 | 0.1~4.0 |
2009年12月至2010年9月共计270 d为路堤施工期;2010年9月至2010年12月为路面施工期;2010年12月至2011年7月为道路运营期。路堤和路面施工期填筑荷载采用线性施加;道路运营期,为模拟交通荷载对地基沉降的影响,按实际交通分流情况,采用等效均布荷载的形式一次施加,拓宽施工期,超车道采用16 kPa,主车道交通荷载采用7 kPa;运营后,原有两车道为小车道,交通荷载采用8 kPa,外侧两拓宽车道为大型货车道,交通荷载采用15 kPa[11]。
3 新旧路基差异沉降预测 3.1 反分析参数及位移特征点的确定 3.1.1 反分析参数的确定
对影响沉降的主要材料参数进行了敏感度分析。结果表明:初始孔隙比e0、压缩曲线斜率λ和临界状态线斜率M的敏感度高,泊松比μ敏感度相对较弱,回弹曲线斜κ率敏感度极其微弱,曲度常量β和屈服应力比K敏感度对计算结果几乎没有影响[12, 13]。因此在实际工程位移反分析时,只需对敏感度高的初始孔隙比e0、压缩曲线斜率λ、临界状态线斜率M和泊松比μ进行位移反分析。对于黏土而言,泊松比μ与土的坚硬状态有关,为了减少数值模拟的复杂程度,可根据经验按地基土流塑状态确定泊松比μ取值。在流固耦合计算中,渗透系数k是地基固结沉降分析的一个最为关键因素,且测定较为困难,离散性大,取值是否合理对结果影响大。为此,本章将对初始孔隙比e0、压缩曲线斜率λ、临界状态线斜率M及渗透系数k共4个参数进行反分析。
3.1.2 位移特征点的确定
根据实测沉降曲线特征,在地基上取4个沉降监测点按两个时段共计8个位移特征点进行位移反分析。其中U1,U2,U3,U4为4个特征点在路堤施工结束时的地基沉降值,其距路堤中心线距离分别为13,18,23 m和27 m;U5,U6,U7,U8为4个特征点在路面施工结束时的地基沉降值,其距路堤中心线距离分别为13,18,23 m和27 m。
3.2 反分析样本设计、网络训练及验证
通过对软土地基物理力学性质分析,初步确定各反分析参数取值范围,见表 2,初始孔隙比e0=0.95~1.15,压缩曲线斜率λ=0.1~0.2,M临界状态线斜率=0.37~0.77,渗透系数k=0.000 1~0.004 m/d。对每个参数取5个代表值进行计算,为了达到数据点分布的均匀性好,试验次数需要54=625次(指数4代表 4个因素,底数5代表每因素有5个水平),该方案中因素和水平的搭配十分全面,缺点是计算次数多。为减少计算工作量,提高工作效率,依据正交试验设计原理,4因素、5水平只需进行25次试验。初始孔隙比e0、压缩曲线斜率λ、临界状态线斜率M及渗透系数k分配方案见表 3。该方法不仅试验次数少,数据点分布均匀,而且结论的可靠性较好。对参数的每个组合进行一次有限元计算,获得8个特征点处垂直位移分量,见表 3。将表中25组材料参数和位移分量作为输入、输出样本,并通过样本训练网络,训练中,网络模型通过遗传算法全局寻优功能,获得的映射fi(x)即为位移反分析的进化神经网络模型。
| 试验组数 | 参数取值 | 竖向位移计算值/m | ||||||||||
| e0 | M | λ | k/(×10-3 m·d-1) | 地基表面关键点与路堤中线距离/m | ||||||||
| 13 | 18 | 23 | 27 | 13 | 18 | 23 | 27 | |||||
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | |||||
| 1 | 0.95 | 0.37 | 0.10 | 0.1 | -0.007 | -0.026 | -0.032 | -0.019 | -0.015 | -0.037 | -0.038 | -0.021 |
| 2 | 0.95 | 0.47 | 0.12 | 1.0 | -0.019 | -0.036 | -0.037 | -0.024 | -0.036 | -0.053 | -0.046 | -0.027 |
| 3 | 0.95 | 0.57 | 0.14 | 2.0 | -0.025 | -0.040 | -0.039 | -0.025 | -0.048 | -0.062 | -0.050 | -0.029 |
| 4 | 0.95 | 0.67 | 0.16 | 3.0 | -0.032 | -0.047 | -0.045 | -0.029 | -0.059 | -0.073 | -0.060 | -0.036 |
| 5 | 0.95 | 0.77 | 0.18 | 4.0 | -0.036 | -0.053 | -0.039 | -0.032 | -0.068 | -0.082 | -0.069 | -0.042 |
| 6 | 1.00 | 0.37 | 0.12 | 2.0 | -0.012 | -0.034 | -0.033 | -0.023 | -0.036 | -0.048 | -0.042 | -0.024 |
| 7 | 1.00 | 0.47 | 0.14 | 3.0 | -0.021 | -0.038 | -0.039 | -0.026 | -0.040 | -0.055 | -0.047 | -0.028 |
| 8 | 1.00 | 0.57 | 0.16 | 4.0 | -0.028 | -0.042 | -0.039 | -0.025 | -0.054 | -0.064 | -0.051 | -0.029 |
| 9 | 1.00 | 0.67 | 0.18 | 0.1 | -0.022 | -0.035 | -0.034 | -0.020 | -0.038 | -0.053 | -0.043 | -0.022 |
| 10 | 1.00 | 0.77 | 0.10 | 1.0 | -0.029 | -0.045 | -0.045 | -0.029 | -0.053 | -0.068 | -0.052 | -0.035 |
| 11 | 1.05 | 0.37 | 0.14 | 4.0 | -0.014 | -0.032 | -0.038 | -0.027 | -0.023 | -0.043 | -0.045 | -0.029 |
| 12 | 1.05 | 0.47 | 0.16 | 0.1 | -0.013 | -0.029 | -0.030 | -0.018 | -0.025 | -0.043 | -0.037 | -0.020 |
| 13 | 1.05 | 0.57 | 0.18 | 1.0 | -0.021 | -0.036 | -0.036 | -0.023 | -0.042 | -0.056 | -0.046 | -0.026 |
| 14 | 1.05 | 0.67 | 0.10 | 2.0 | -0.025 | -0.043 | -0.043 | -0.028 | -0.046 | -0.063 | -0.055 | -0.034 |
| 15 | 1.05 | 0.77 | 0.12 | 3.0 | -0.030 | -0.048 | -0.050 | -0.033 | -0.053 | -0.071 | -0.053 | -0.041 |
| 16 | 1.10 | 0.37 | 0.16 | 1.0 | -0.012 | -0.030 | -0.036 | -0.024 | -0.021 | -0.041 | -0.043 | -0.027 |
| 17 | 1.10 | 0.47 | 0.18 | 2.0 | -0.020 | -0.036 | -0.037 | -0.024 | -0.039 | -0.053 | -0.045 | -0.026 |
| 18 | 1.10 | 0.57 | 0.10 | 3.0 | -0.024 | -0.040 | -0.039 | -0.025 | -0.044 | -0.059 | -0.049 | -0.029 |
| 19 | 1.10 | 0.67 | 0.12 | 4.0 | -0.029 | -0.045 | -0.044 | -0.029 | -0.053 | -0.068 | -0.057 | -0.035 |
| 20 | 1.10 | 0.77 | 0.14 | 0.1 | -0.020 | -0.035 | -0.034 | -0.020 | -0.035 | -0.051 | -0.043 | -0.023 |
| 21 | 1.15 | 0.37 | 0.18 | 3.0 | -0.013 | -0.031 | -0.037 | -0.025 | -0.022 | -0.042 | -0.043 | -0.028 |
| 22 | 1.15 | 0.47 | 0.10 | 4.0 | -0.020 | -0.036 | -0.037 | -0.024 | -0.037 | -0.053 | -0.045 | -0.027 |
| 23 | 1.15 | 0.57 | 0.12 | 0.1 | -0.015 | -0.030 | -0.030 | -0.017 | -0.028 | -0.044 | -0.037 | -0.019 |
| 24 | 1.15 | 0.67 | 0.14 | 1.0 | -0.022 | -0.038 | -0.037 | -0.024 | -0.042 | -0.058 | -0.049 | -0.028 |
| 25 | 1.15 | 0.77 | 0.16 | 2.0 | -0.026 | -0.044 | -0.044 | -0.028 | -0.049 | -0.067 | -0.058 | -0.037 |
为了验证进化神经网络的反分析效果,将表 4中材料参数输入已建立的有限元计算模型,其余参数同表 1和表 2,获得了地基表面8个特征点竖向位移分量,然后将8个特征点竖向位移分量输入训练得到的进化神经网络模型进行反分析,位移反分析结果与有限元输入材料参数吻合较好,见表 4。分析表明,采用该方法进行沉降预测是可行的。
| 材料参数 | 反分析结果 | 有限元输入材料参数 | 相对误差/% |
| e0 | 1.043 | 1.04 | 0.29 |
| M | 0.392 | 0.40 | 0.51 |
| λ | 0.159 | 0.16 | 0.63 |
| k/(×10-3m·d-1) | 1.977 | 2.00 | 1.15 |
将实测值断面上8个特征值作为输入值,通过训练好的进化网络模型进行位移反分析,获得了初始孔隙比e0、压缩曲线斜率λ、临界状态线斜率M渗透系数k共 4个材料参数值,分别为1.01,0.142,0.53 m/d和0.001 3 m/d。把反分析获得的材料参数和其他材料参数输入有限元计算模型,即可进行地基固结沉降分析,并可对工后地基沉降进行预测。
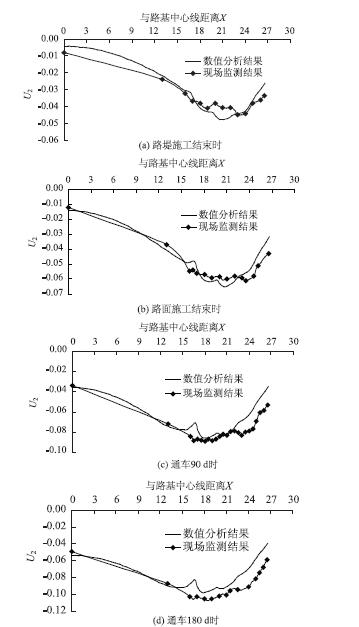
图 2(a)为路堤施工结束时地基横断面沉降曲线,图 2(b)为路面施工结束时地基横断面沉降曲线。图中,数值分析结果和现场监测结果基本一致,说明反分析得到的材料参数与实际相吻合。图 2(c)和图 2(d)分别为通车90 d和188 d时地基横断面沉降曲线,分析表明,通过反分析得到的数值分析结果和后期现场监测结果基本一致,说明该反分析法获得的参数值可用于预测工后沉降。
|
| 图 2 地基横断面沉降曲线(单位:m) Fig. 2 Curves of foundation cross-sectional settlement(unit:m) |
从上述图中进一步分析可知,路堤拓宽期间,地基沉降最大点并不是拓宽路堤荷载的形心位置,而是位于路肩外2 m处;路面施工期间,地基沉降最大点仍位于路肩外2 m处,但路面施工期内,新旧路堤搭接处沉降量和沉降速率开始大于路肩处;道路通车188 d,由于车辆荷载作用,拓宽路堤沉降趋势进一步向路堤中心发展,通车90 d和188 d时,数值分析结果和现场监测结果的地基沉降最大点均位于距离路堤中心18 m处。
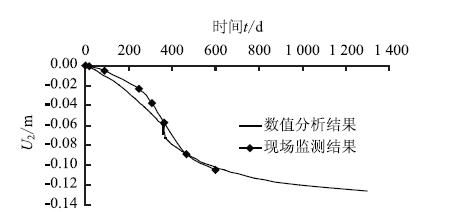
图 3为距离路堤中心18 m处地基沉降随时间的变化曲线。在路堤施工期,反分析计算结果略大于现场监测结果;在路面施工期,由于工期紧,路面施工速度快,现场监测结果中地基沉降速率大于数值计算结果,这是由于数值分析中把路面荷载按时间线性施加,且未考虑施工机械作用对地基沉降的影响;在道路通车期间,由于数值分析中将交通荷载等效为均布荷载一次施加,导致通车初期沉降速率明显大于现场实测结果,但在道路运营一段时间后,地基工后沉降量和沉降速率基本一致。
|
| 图 3 距离路基中心18 m处地基沉降随时间的变化曲线 Fig. 3 Foundation settlement at position of 18 m from subgrade center varying with time |
将预测结果与现场实测结果比较,二者在地基横断面沉降曲线分布规律和沉降随时间的变化上变化预形趋势一致性均较好。预测结果与现场实测结果的相对误差见表 5,表中除个别点相对误差略大于10%外,其余均小于10%。总体上,在公路拓宽工程这种复杂地基条件下,预测结果比较理想,可满足工程应用的需求。分析表明,通过基于位移反分析的有限元预测方法对道路工后沉降进行预测是可行的。
| 地基沉降各阶段 | 与旧路基中心距离/m | ||
| 13 | 18 | 23 | |
| 路堤施工期 | 10.1 | 9.2 | 3.1 |
| 路面施工期 | 7.8 | 6.5 | 7.6 |
| 运营188 d | 1.3 | 3.7 | 12.5 |
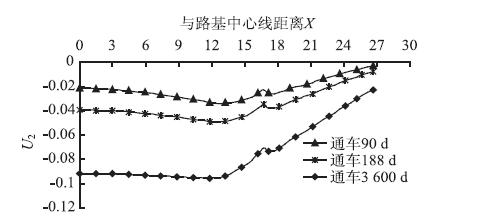
图 4为地基横断面沉降盆图。地基工后沉降最大值位于距离路堤中心13 m处,这与两年多来的监测结果和路面变形情况相符合。福泉厦高速公路扩建工程竣工通车至今,新旧路基搭接处差异沉降大,局部出现了纵向裂缝。
|
| 图 4 地基横断面工后沉降盆图(单位:m) Fig. 4 Curves of foundation cross-sectional settlement basin after construction(unit:m) |
由于文章篇幅有限,以上仅以CFG桩处理软基进行了分析,在工程研究中,还对浅层换填、PTC桩处理软基进行了分析比较,得出结论如下:
(1)基于位移反分析的有限元预测方法克服了传统预测方法只能预测单点沉降的缺点,实现了路基全断面沉降预测,预测结果与现场实测结果一致较好,时效性高,是公路拓宽工程这种复杂工程问题中进行施工期及工后沉降预测的理想方法。该预测方法已成功应用于福泉厦高速公路扩建工程,预测结果指导了路基路面的设计和施工。
(2)施工期间,横断面内地基沉降最大点位于路肩外侧1~2 m位置,而非拓宽路堤荷载的形心位置;道路通车一段时间后,在路堤自身重力荷载和交通荷载的共同作用下,地基沉降向新旧路堤搭接处发展。研究表明,工后沉降最大点位于距离路堤中心11~16 m位置,具体位置与拓宽软基处理方式有关:对换填处理的浅层软基,位于距离路堤中心16 m位置左右;对CFG或PTC桩处理的深厚软基,位于距离路堤中心11 m位置左右。因此,需要结合新旧地基差异沉降特性,提高新旧路基接合部地基和路基路面的设计和施工要求。
(3)研究表明:双向四车道两边拓宽为八车道的拓宽工程中,采用CFG桩或PTC桩对软基进行处理可以显著降低新、旧地基总沉降和旧路地基工后横坡比改变量,但由于工后横断面内最大沉降点发生在新旧路基搭接处附近,拓宽路堤工后横坡比改变量反向增大,引起路面内倾。因此,在软土地基拓宽工程设计路拱坡度时,应采用较大值,以避免拓宽路堤内倾抵消部分路拱坡度,减弱路面排水能力,且在路面养护过程中,对新旧路基搭接处位置附近的路面病害必须及时处理,以避免裂缝受雨水、车载等外部坏境加剧病害的发展。
| [1] | 王丙兴.考虑软土结构性损伤的路基沉降预测反分析[J].公路交通科技,2011,28(1):47-51.WANG Bing-xing. Back Analysis of Forecasting Road Foundation Settlement Considering Structural Damnification of Soil[J]. Journal of Highway and Transportation Reserarch and Development, 2011,28(1):47-51. |
| [2] | 王丙兴.基于ABAQUS的公路软基沉降预测非概率可靠度研究[J].公路交通科技,2012,29(4):1-3.WANG Bing-xing. Research on Nonprobabilisitic Reliability for Prediction of Sedimentation of Soft Roadbeds of Highways Based on ABAQUS[J]. Journal of Highway and Transportation Reserarch and Development, 2012,29(4):1-3. |
| [3] | 李西斌.高速公路软土地基沉降预测方法现状探讨[J].公路,2011(5):16-20.LI Xi-bin. Summary of Forecasting Methods of Expressway Settlement on Soft Clay Subgrade [J].Highway, 2011(5):16-20. |
| [4] | 朱培良,高金康,朱晓艳.软土路基沉降预测的参数反演分析研究[J].浙江交通职业技术学院学报,2011,12(3):13-15.ZHU Pei-liang, GAO Jin-kang, ZHU Xiao-yan. Study on Parameter Inversion of Settlement Forecast for Softsoil Roadbed[J]. Journal of Zhejiang Institute of Communications,2011,12(3):13-15. |
| [5] | 吕秀杰.软土地基工后沉降预测模型的研究[J].岩土力学,2009,30(7):2092-2097.LV Xiu-jie. Research on Estimation Model of Post Construction Settlement for Soft Ground[J]. Rock and Soil Mechanics,2009,30(7):2092-2097. |
| [6] | 李端有,甘孝清,周武.基于均匀设计及遗传神经网络的大坝力学参数反分析方法[J].岩土工程学报,2007,29(1):125-130.LI Duan-you, GAN Xiao-qing, ZHOU Wu. Back Analysis on Mechanical Parameters of Dams Based on Uniform Design and Genetic Neural Network[J]. Chinese Journal of Geotechnical Engineering, 2007,29(1):125-130. |
| [7] | 张永清,王选仓,王曹晖.拓宽路基差异沉降计算参数的确定[J].长安大学学报:自然科学版,2009,29(2):13-18.ZHANG Yong-qing,WANG Xuan-cang,WANG Cao-hui. Calculation Parameter Determination of Widened Subgrade Difference Settlement[J]. Journal of Chang'an University:National Science,2009,29(2):13-18. |
| [8] | MENG De-guang, ZHU Tian-zhi, LI Bing-xin, et al. Research for Settlement Prediction on the Based of Neural Network and ADINA[C]// Proceedings of International Forum on Computer Science-Technology and Applications(Volume:3 ).Chongqing: IEEE, 2009:123-126. |
| [9] | WANG Zhi-liang, LI Yong-chi, SHEN R F. Correction of Soil Parameters in Calculation of Embankment Settlement Using a BP NetworkBack Analysis Model[J]. Engineering Geology, 2007, 91(2/3/4):168-177. |
| [10] | 傅鹤林,彭思甜,韩汝才,等.岩土工程数值分析新方法[M].长沙:中南大学出版社,2006.FU He-lin, PENG Si-tian, HAN Ru-cai, et al. A New Numerical Method for Geotechnical Engineering Analysis[M], Changsha:Central South University Press,2006. |
| [11] | 梅英宝. 交通荷载作用下道路与软土复合地基共同作用性状研究[D]. 杭州:浙江大学,2004.MEI Ying-bao. Study on Interaction Characteristics of Road and Soft Soil Composite Foundation under Traffic Load [D]. Hangzhou:Zhejiang University,2004. |
| [12] | 陈治伙.修正剑桥模型参数敏感性分析[J].福建交通科技,2012,12(1):13-15.CHEN Zhi-huo. Analysis of Modified Cambridge Model Parameter Sensitivity [J]. Fujian Transport Science and Technology,2012,12(1):13-15. |
| [13] | 陈治伙.拓宽工程软基差异沉降影响因素及其敏感性分析[J].福建建设科技,2012 (2):67-71.CHEN Zhi-huo. Analysis of the Factors and Sensitivity of the Settlement Difference of Widening Project on Soft Foundation[J]. Fujian Construction Science & Technology,2012 (2):67-71. |
 2015, Vol. 31
2015, Vol. 31
