扩展功能
文章信息
- 向波, 何思明, 庄卫林, 王东坡
- XIANG Bo, HE Si-ming, ZHUANG Wei-lin, WANG Dong-po
- 滚石冲击荷载下垫层材料的动力响应研究
- Research on Dynamic Response of Cushion under Rockfall Impact
- 公路交通科技, 2015, Vol. 31 (1): 45-49
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 45-49
- 10.3969/j.issn.1002-0268.2015.01.008
-
文章历史
- 收稿日期:2013-11-07
2. 中国科学院水利部成都山地灾害与 环境研究所, 四川 成都 610041
2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu Sichuan 610041, China
滚石是个别块石因某种原因从地质体表面失稳后经过下落、回弹、跳跃、滚动或滑动中的一种或几种组合运动方式沿坡面快速下移,最后在平缓地带或障碍物附近静止下来的一个动力演化过程。当滚石运动范围内有人类活动或构筑设施并引起一定损失时,就构成滚石灾害[1]。我国西部山区起伏陡峻,地质条件复杂,构造运动强烈,气候复杂多变,山体破碎,导致滚石灾害频发,对区内公路构筑物和人类活动构成严重威胁。特别是5·12地震后,崩塌滚石灾害大规模爆发,沿江沿线成群发生。
近年来,国内外学者对滚石灾害的基础研究愈发重视[2, 3, 4, 5, 6, 7, 8]。An[9]采用离散元研究了滚石的非弹性冲击问题。Delhomme[10]等研究了滚石耗能减震防护结构。Kishi等[11]研究了钢筋混凝土滚石防护结构的极限冲击力。Pichler等[12]研究了砂砾石垫层材料的冲击响应问题。然而,从整体上看,国内外对崩塌滚石灾害防治的基础理论研究还比较薄弱,有关滚石冲击力计算、冲击能量确定等关键科学问题还没有系统成果,相关设计主要依据经验或简易公式,存在较大的风险。
棚洞是山区交通干线滚石灾害防护最有效的手段,通过在棚洞顶板上铺设一层土石垫层材料来耗散滚石冲击能量,从而达到保护棚洞的目的。为此,在将滚石-棚洞冲击模型转化为刚性球自由落体碰撞问题的前提下,以Hertz接触理论为基础,考虑到垫层土体的非弹性变形,结合动力有限元数值仿真技术,研究滚石对垫层的法向冲击特性,揭示滚石冲击速度、滚石半径对垫层土体动力响应的影响,为滚石防护棚洞垫层结构优化设计提供理论基础。
1 问题描述
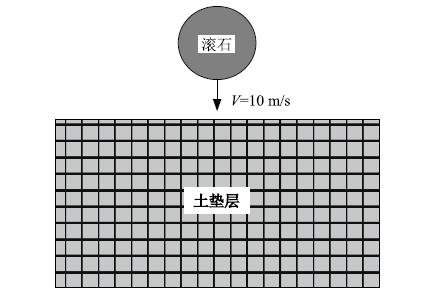
对于滚石对棚洞垫层结构的法向冲击问题,由于滚石相对刚度较大,可视为刚体,见图 1。为研究简便,特假设:棚洞垫层材料为均匀、各向同性弹塑性体;滚石为刚性球体。
|
| 图 1 滚石冲击垫层计算模型 Fig. 1 Calculation model of rockfall impact on cushion |
取滚石半径R=0.8 m,密度ρ=2 500 kg/m3,质量m=5 359 kg,转动惯量I=1 371.6 kg·m2。垫层结构几何尺寸为10 m×10 m×3 m,相关物理力学指标见表 1。
| 土垫层 | 滚石 | ||||||
| 重度/(kN·m-3) | 弹性模量/MPa | 泊松比 | 屈服压强/kPa | 摩擦角/(°) | 膨胀角/(°) | 重度/(kN·m-3) | 冲击速度/(m·s-2) |
| 20.5 | 46 | 0.3 | 400 | 40 | 0 | 25 | 12 |
因文章旨在研究不同滚石冲击能量下垫层的动力响应问题,为此进行了以下工作。
(1)计算了滚石特定冲击速度(V=12 m/s)下垫层的接触变形,分析了接触力-时间曲线、压入位移-时间曲线、能量-时间曲线、滚石速度-时间曲线、接触面半径-时间曲线、接触力-压入深度曲线,给出了接触力最大时垫层不同厚度剖面的压力分布。
(2)分析了垫层在不同滚石冲击速度(V=6,8,10,12,16,20,24 m/s)下的接触响应问题,给出了最大接触力-速度曲线、最大压入深度-速度曲线、回弹系数-速度曲线。
2 有限元模型的建立
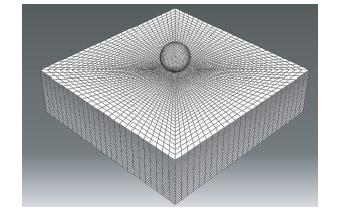
基于问题分析,借助Abaqus强大的建模、计算、分析功能,构建图 2所示的刚性球体-弹塑性体的冲击接触模型。其中球体采用Hex-dominated六面体单元的Sweep模式进行剖分,方形平板采用Hex-dominated六面体单元的Structured进行剖分,与球体冲击接触部分的网格相对密集。
|
| 图 2 数值模拟模型 Fig. 2 Numerical simulation model |
(1)材料设置:土垫层弹性模量为4.6 Gpa,泊松比为0.3;在D-P模型中摩擦角、角膨胀系数等参数通过Plastic/Drucker-Prager设定,对应流动应力比为1。Drucker-Prager Hardening选项中强化类型为Compression,屈服应力为400 kPa。
(2)滚石设置:滚石刚体中心要设置参考点,并在参考点建立一个Inertias,添加质量和转动惯量。
(3)接触设置:滚石下表面区域和垫层中间1.6 m×1.6 m方形区域设置面面接触。由于无切向行为,切向摩擦系数设为无摩擦。
(4)边界约束:滚石为自由落体,垫层底部节点约束3个方向的平动自由度。
(5)分析步设置:设动态显式(Dynamic Explicit)分析步为Step-1。分析步的时间为0.06,时间增量类型为自适应,限定最大值为10-5。
(6)输出设置:在时间历程输出中,除默认输出外,需添加接触力、接触面积输出,即将Domain选为Interaction,选择Contact中的CFN和CAREA,再将Domain选为Set,先前将滚石中心设为Set-1,选择Displacement里的U2。将场输出和时间历程输出的间隔时间都设为0.000 2 s。
(7)加载设置:在Initial分析步中,给滚石参考点一个初速度。
3 计算结果与敏感度对比分析 3.1 半径0.8 m滚石以12 m/s速度冲击的结果
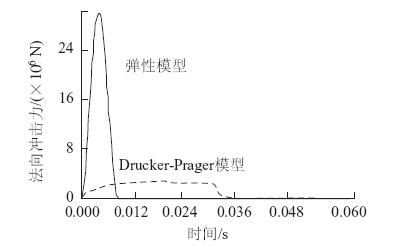
图 3计算了弹性和弹塑性两种不同垫层材料对滚石法向冲击的响应曲线。
|
| 图 3 法向冲击力时程曲线 Fig. 3 Curves of normal impact force time history |
显然,完全弹性垫层承担的冲击力较大,其极值(3×107 N)约是弹塑性解(3×106 N)的10倍,这说明具有弹塑性性质的土石垫层可以很好地降低作用于结构上的冲击力。同时弹塑性D-P模型的冲击历时(0.036 s)远大于理想弹性模型,这也反映了垫层塑性变形性质对耗散滚石的冲击,降低冲击压力至关重要。
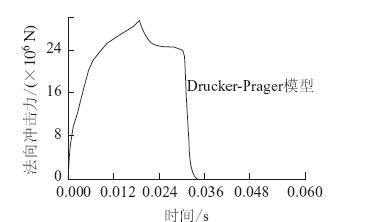
图 4给出了D-P模型计算的滚石法向冲击力时程曲线。可以看出,垫层材料对滚石冲击能量的耗散主要是在前[0.01 s,0.031 s]的塑性接触变形内完成的,约占80%的冲击总能量,远大于时域[0 s,0.01 s]内的弹性变形耗能。
|
| 图 4 D-P模型冲击力时程曲线 Fig. 4 Curve of impact force time history calculated by D-P model |
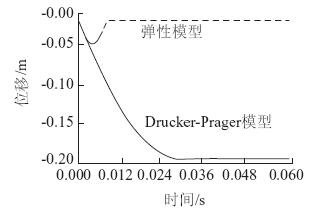
图 5为滚石对完全弹性和D-P弹塑性两种材料垫层的冲击变形曲线。可以看出,D-P材料垫层无论变形量还是变形时程都远大于弹性垫层,最大量为0.195 m的压入变形远大于弹性垫层的0.034 m,相应的历时0.032 s也远大于弹性材料垫层的0.008 s。这说明弹塑性垫层材料可通过自身变形很好地延长作用时间,降低冲击,达到耗能缓冲的效果。
|
| 图 5 压入位移时程曲线 Fig. 5 Curves of cushion indentation time history |
特别强调,理论上滚石冲击弹性垫层的过程是一个冲击-弹跳-再冲击的往复循环过程,即由于缺乏有效的能量耗散机制,滚石对弹性垫层的冲击次数要远多于弹塑性垫层,并导致垫层材料及棚洞结构的损伤累积破坏出现。相反,弹塑性材料不仅具有单次强烈耗能的效果,还防止了往复荷载的出现,避免了结构时程上的累积损伤破坏。
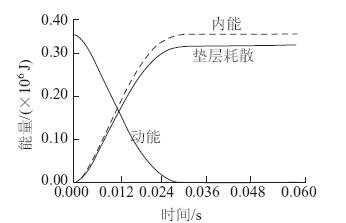
图 6为滚石冲击垫层过程中的能量转化关系。可以看出,随着接触时间的增加和垫层压入变形的增大,滚石的动能在迅速减小。若定义回弹恢复系数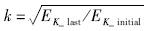 ,则通过计算k=0.037 8可以发现,真正用于滚石弹性回弹的能量只占1/30,大部分能量被垫层的塑性变形耗散了。
,则通过计算k=0.037 8可以发现,真正用于滚石弹性回弹的能量只占1/30,大部分能量被垫层的塑性变形耗散了。
|
| 图 6 D-P模型的能量时程曲线 Fig. 6 Curves of energy calculated by D-P model |
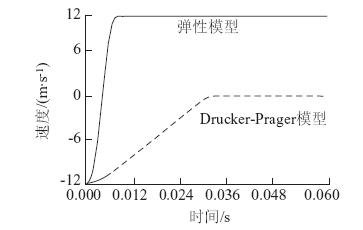
图 7为完全弹性和D-P弹塑性两种材料垫层上滚石冲击速度的时程曲线。可以看出,作用在弹性垫层材料上的滚石速度先迅速减小,后迅速增大反弹。整个接触只是滚石动能和垫层弹性变形能相互转化的过程,并无能量耗散,加之单次冲击历时短变形小使得缓冲效果差。反之,D-P材料垫层上的滚石则未出现明显反弹,即滚石首次的冲击动能几乎全被D-P垫层耗散掉了。
|
| 图 7 滚石冲击速度时程曲线 Fig. 7 Curves of rockfall impact velocity time history |
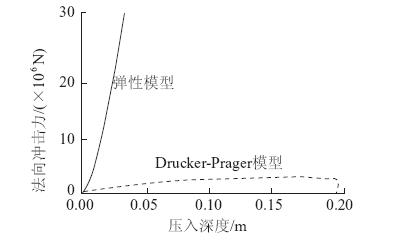
图 8为完全弹性和D-P弹塑性两种材料垫层上冲击力与压入深度的时程曲线。可以看出,弹性材料的压入深度较小,冲击力较大,整条曲线符合Hertz接触理论解。而D-P材料垫层上的冲击力随接触压入深度的变化不大,略微增加部分为接触面积增加所致。实际上,在某个极值速度下,滚石为陷入垫层,此时滚石冲击力达到极值,随后不再随压入变形的增加而变化。可见,垫层的最佳耗能状态发生在滚石恰好可以陷入的时刻。
|
| 图 8 冲击力-压入深度曲线 Fig. 8 Relation between impact force and cushion indentation |
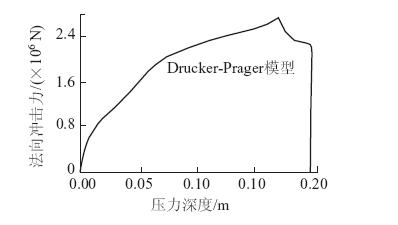
理论上,滚石最大冲击力应出现在压入变形最大处,然而实际结果计算表明最大冲击力Fmax=2 833 kN出现在t= 0.018 4 s时(图 9),而最大压入深度hmax=0.194 942 m却出现在t=0.029 6 s,这主要是因为理论的静态分析不能真实反映动荷载的冲击变形过程。
|
| 图 9 D-P模型的冲击力与压入深度关系 Fig. 9 Relation between impact force and cushion indentation calculated by D-P model |
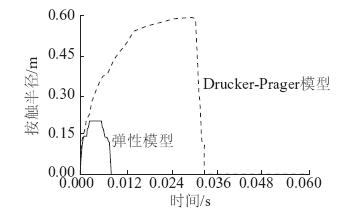
图 10为球体对完全弹性和D-P弹塑性两种不同材料垫层冲击时的接触半径时程曲线。可以看出,弹性材料垫层的接触半径在0.04 s达到最大,远早于弹塑性垫层(0.032 s)。同时弹性垫层材料的冲击回弹过程是对称的,而弹塑性材料则很少回弹。
|
| 图 10 接触面半径的时程曲线 Fig. 10 Curves of contact surface radius time history |
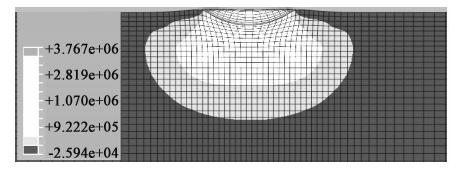
从图 11给出的接触力最大时垫层剖面压应力的分布可见,接触中心压应力最大(2 MPa),周围应力近似环状向外扩散,这与相关接触理论一致。
|
| 图 11 接触力最大时垫层剖面压应力云图(单位:MPa) Fig. 11 Nephogram of compressive stresses of cushion section in maximum contact force(unit:MPa) |
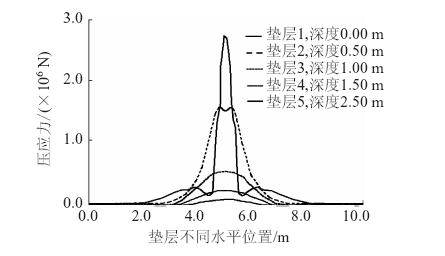
图 12计算了多层复合垫层上压应力的分布。可以看出,深度大的下层垫层接触压应力小的多,而表层第1层的压应力最大。
|
| 图 12 不同深度垫层的压应力布 Fig. 12 Distribution of compressive stresses of cushion in different depths |
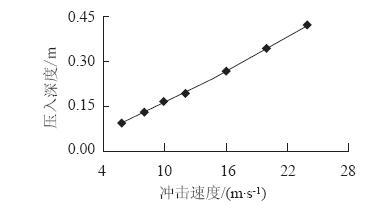
图 13为滚石冲击压入深度和速度的关系曲线。可以很明显地看出,随着滚石冲击速度的增加,垫层的压入深度也明显增大。这种趋势在高速下更为明显,这主要是因为垫层材料的耗能效率在滚石冲击贯入后就不再增加导致的。
|
| 图 13 压入深度-速度曲线 Fig. 13 Curve of indentation vs. velocity |
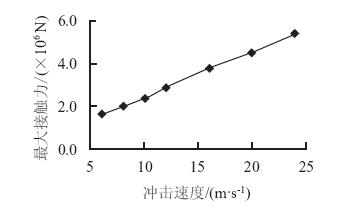
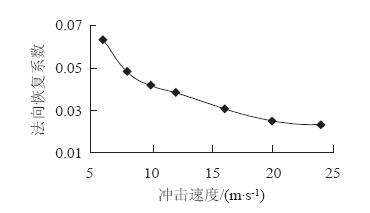
图 14所示的滚石冲击速度和最大接触力关系曲线也基本反映了上述规律,即冲击速度越大,接触压力越大。但对应回弹恢复系数却发生了很大变化,冲击速度越大,回弹恢复系数越小(图 15),主要原因在于滚石冲击速度越高,大部分能量转化为垫层的塑性变形,弹性能所占比例越来越低所致。
|
| 图 14 最大接触力-速度曲线 Fig. 14 Curve of maximum contact force vs. velocity |
|
| 图 15 恢复系数-速度曲线 Fig. 15 Curve of restitution coefficient vs. velocity |
考虑到滚石刚度远高于地面土体刚度,将滚石对垫层土体的法向冲击简化为刚性球体对半无限体的法向冲击问题,借助动力有限元分析手段分别分析了弹性、弹塑性两种不同材料垫层对滚石法向冲击的响应问题,并得出以下结论:
(1) Hertz完全弹性接触理论模型没有考虑冲击过程中垫层土体可能产生的塑性变形,计算的滚石冲击力非常大,冲击深度很小,计算结果无法应用于实际滚石防治工程结构设计。
(2) 在考虑棚洞垫层土体的弹塑性特性后,滚石冲击能量主要用于垫层土体的塑性变形,这与弹性垫层有很大区别。
(3)冲击速度越大,弹塑性的垫层土体冲击力和冲击深度越大,对应回弹恢复系数却在变小,并趋于稳定,反映出高速冲击下垫层土体的耗能效果仍然很好。
(4)弹塑性的垫层土体可以很好地耗散滚石冲击能量,也可以大大缓和作用在结构上的冲击力,起到耗能缓冲的效果。
| [1] | 张路青,许兵,尚彦军,等. 川藏公路南线八宿—林芝段滚石灾害的工程地质调查与评价[J]. 岩石力学与工程学报, 2004,23(9):1551-1557.ZHANG Lu-qing, XU Bing, SHANG Yan-jun, et al. Engineering Geological Investigation and Assessment on Rockfall Hazard along Basu-Linzhi Section of south Sichuan-Tibet highway [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(9): 1551-1557. |
| [2] | 何思明,吴永,杨雪莲.滚石坡面冲击回弹规律研究[J].岩石力学与工程学报,2008,27(增1):2794-2798.HE Si-ming, WU Yong, YANG Xue-lian. Study of Rock-fall Motion on Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2794-2798. |
| [3] | 何思明,吴永,李新坡.滚石冲击碰撞恢复系数研究[J].岩土力学,2009,30(3):623-627.HE Si-ming, WU Yong, LI Xin-po. Research on Restitution Coefficient of Rock Fall[J]. Rock and Soil Mechanics, 2009, 30(3): 623-627. |
| [4] | 何思明,李新坡,吴永.滚石冲击荷载作用下土体屈服特性研究[J].岩石力学与工程学报,2008,27(增1):2972-2977.HE Si-ming, LI Xin-po, WU Yong. Research on Yield Property of Soil under Rock-fall Impact[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2972-2977. |
| [5] | 沈均, 何思明, 吴永. 滚石灾害研究现状及发展趋势[J]. 灾害学, 2008, 23(4): 122-125.SHEN Jun, HE Si-ming, WU Yong. Present Research Status and Development Trend of Rockfall Hazards[J]. Journal of Catastrophology, 2008,23(4): 122-125. |
| [6] | CHAN K S, LEE Y. A Fracture Mechanics-based Model for Assessing the Mechanical Failure of Nuclear Fuel Rods due to Rock Fall[J]. Nuclear Engineering and Design, 2000, 201(2/3): 209-226. |
| [7] | CHAU K T, WONG R H C, WU J J. Coefficient of Restitution and Rotational Motions of Rock-fall Impacts [J]. |
| [8] | AN B. A Study of Energy Loss during Rock Impact Using PFC2D [M]. Edmonton: University of Alberta, 2006. |
| [9] | AN B, TANNANT D D. Discrete Element Method Contact Model for Dynamic Simulation of Inelastic Rock Impact [J]. |
| [10] | DELHOMME F, MOMMESSIN M, MOUGIN J P, et al. Behavior of a Structurally Dissipating Rock-shed: Experimental Analysis and Study of Punching Effects [J]. |
| [11] | KISHI N, KONNO H, IKEDA K, et al. Prototype Impact Tests on Ultimate Impact Resistance of PC Rock-sheds [J]. |
| [12] | PICHLER B, HELLMICH C, MANG H A. Impact of Rocks onto Gravel Design and Evaluation of Experiments [J]. |
 2015, Vol. 31
2015, Vol. 31
