扩展功能
文章信息
- 林云青, 谈至明
- LIN Yun-qing, TAN Zhi-ming
- 水泥混凝土路面的温度梯度日极值预估
- Estimation of Diurnal Extreme of Cement Concrete Pavement Temperature Gradient
- 公路交通科技, 2015, Vol. 31 (1): 41-44
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 41-44
- 10.3969/j.issn.1002-0268.2015.01.007
-
文章历史
- 收稿日期:2014-01-02
2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China
我国公路建设正处于一个快速发展阶段,水泥混凝土路面结构形式的应用较为广泛。水泥混凝土路面的疲劳开裂主要是由荷载应力和温度应力共同作用引起的。影响温度应力大小的,除了路面本身结构外,主要是路面温度梯度[1]。温度梯度的大小受外界环境如气温、辐射、风雨等因素的影响较为显著。由于这些影响因素的复杂性和多样性,使得至今没有一个适用于各种情况的预估模型。本文基于大同、宁波、广州三地路面温度场实测站采集的一年以上路面温度数据,分析了水泥混凝土路面温度梯度极值的变化规律,尝试建立水泥混凝土路面温度梯度日极值的预估模型。
1 国内外研究概况
路面结构的温度状况研究一直被国内外道路工作者所重视,研究方法分为两类[2, 3]:(1)统计分析法,通过实测路面结构层内温度和采集当地气象要素资料(太阳辐射、气温、日照时间、地表温度、风速、降水等),利用统计学的方法进行回归分析,建立路面温度场与环境气象参数的关系;(2)理论分析法,根据气象学和传热学的基本原理采用数值分析方法建立路面温度场的预测模型。
1931—1934年间,在美国Arlington试验中心对水泥混凝土路面的温度状态进行了大量的实测,得出了可供设计计算应用的最大正负温度梯度[2]。之后,日本近藤佳宏等人根据路面温度实测结果指出,路面结构内不同深度处的最高或最低温度与路表温度及气温之间呈线性关系,路面结构温度日变化可近似为二个正弦的周期函数[4]。
1982年,谢国忠等人回归得到了晴天水泥混凝土路面最大温度梯度值Tg.max与日全辐射Q、日温差ΔTa的近似关系式[3]。1991年,徐世法以2 a的气温和路面实测数据为依据,分析了北京地区沥青路面温度的分布规律。建立了路面各层温度与路表温度、平均温度、最高气温、最低气温之间的回归关系[6]。2004年,秦健、孙立军等人根据上海、石家庄、新疆等地区路面温度场实测数据和当地气象资料,建立了预估沥青路面不同深度处小时温度与当前气温、太阳辐射强度、此前5 h平均气温,以及30 a平均气温4个自变量的模型[7, 8]。2008年,贾璐、胡晓等人在秦健模型的基础上进行了改进[9]。2009年,谈至明、邹晓翎等人在广州、宁波、大同等地设立了路面温度观测站,进行了1 a以上的实测,建立了普适性和精度良好的路表温度日极值(最高、最低)的估算式和可反映日长、日间最低温度差异等因素的路面温度日变化规律的拟合模型[10, 11]。
本文对水泥混凝土路面温度梯度日极值的研究基于广州、宁波、大同3个路面温度观测站的实测数据作为建模基础。
2 基于气象要素的温度梯度日最大值预估模型
与水泥混凝土路面温度梯度相关性最密切的气象要素有太阳辐射量和气温这2项。太阳辐射是路面热量的来源,而气温则是路面热交换的直接对象。影响太阳全辐射量大小的因素主要有大气的浑浊度、太阳高度角和云层的反射率等,晴天太阳总辐射量较高,接近理论太阳总辐射值,而雨天或多云天气太阳总辐射量较低,但关系复杂,规律难寻。影响路面与空气热交换量的因素有风速,降雨量等。
大同、宁波、广州三地的标准厚度(22 cm)水泥混凝土路面日最大温度梯度( )与各气象要素(日太阳总辐射Q、日气温差ΔTa、前一天太阳总辐射Q-1、日平均风速v、日降水量R、日平均云量C)之间的相关性见表 1。从表 1可以看出,水泥混凝土路面日最高温度梯度与日太阳总辐射Q、日温差ΔTa、前一天太阳总辐射Q-1相关性较好。
)与各气象要素(日太阳总辐射Q、日气温差ΔTa、前一天太阳总辐射Q-1、日平均风速v、日降水量R、日平均云量C)之间的相关性见表 1。从表 1可以看出,水泥混凝土路面日最高温度梯度与日太阳总辐射Q、日温差ΔTa、前一天太阳总辐射Q-1相关性较好。
| 测站 | Q | ΔTa | Q-1 | v | R | C |
| 大同 | 0.872 | 0.624 | 0.577 | -0.006 | -0.340 | -0.342 |
| 宁波 | 0.905 | 0.697 | 0.467 | -0.180 | -0.361 | -0.730 |
| 广州 | 0.876 | 0.645 | 0.554 | -0.147 | -0.275 | -0.699 |
因此,取日太阳总辐射Q、日温差ΔTa、前一天太阳总辐射Q-1作为基本变量的水泥混凝土路面日最大温度梯度预估模型为:
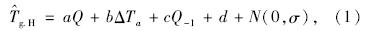
 为标准厚度水泥混凝土路面的日最大温度梯度;Q为日太阳总辐射;ΔTa为日气温差;Q-1为前一天太阳总辐射;a,b,c,d为回归系数,其值见表 2;N(0,σ)为标准正态函数;σ为回归残差标准差。各项参数取值见表 2。
为标准厚度水泥混凝土路面的日最大温度梯度;Q为日太阳总辐射;ΔTa为日气温差;Q-1为前一天太阳总辐射;a,b,c,d为回归系数,其值见表 2;N(0,σ)为标准正态函数;σ为回归残差标准差。各项参数取值见表 2。
| 测站 | a | b | c | d | σ/(℃·m-1) | R2 |
| 大同 | 2.47 | 1.46 | 0.174 | -8.60 | 9.30 | 0.924 |
| 宁波 | 3.38 | 1.85 | -0.086 | -5.60 | 10.2 | 0.941 |
| 广州 | 2.08 | 1.45 | -0.151 | -6.23 | 5.50 | 0.900 |
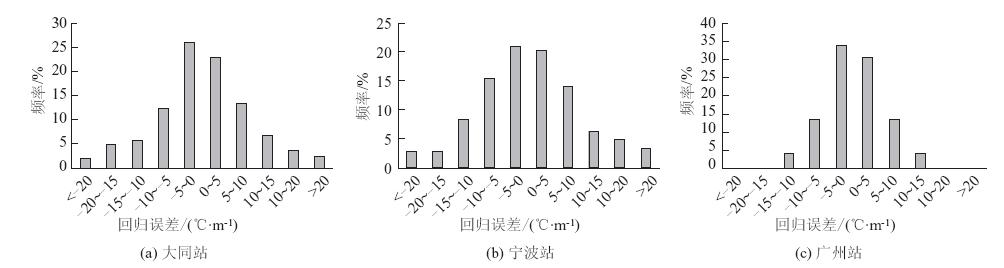
图 1为给出了式(1)回归误差(实测值-模型估计值)的频率分布图。从图 1可以看出,模型估计值与实测结果能较好地吻合,离散性较小,式(1)推算水泥混凝土路面日最大温度梯度的误差位于-10~10 ℃/m之间的频率分别为81%,71%和91%。
|
| 图 1 式(1)回归误差的频率分布 Fig. 1 Frequency distribution of regression errors of Equation (1) |
以路表温度日最高、最低值Ts.max、Ts.min为自变量的水泥混凝土路面日最高温度梯度 预估模型为:
预估模型为:
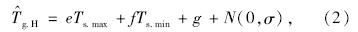
| 测站 | e | f | g | σ/(℃·m-1) | R2 |
| 大同站 | 3.05 | -2.89 | -10.22 | 5.65 | 0.975 |
| 宁波站 | 3.36 | -2.98 | -14.56 | 6.17 | 0.979 |
| 广州站 | 3.19 | -2.99 | -7.30 | 3.86 | 0.977 |
|
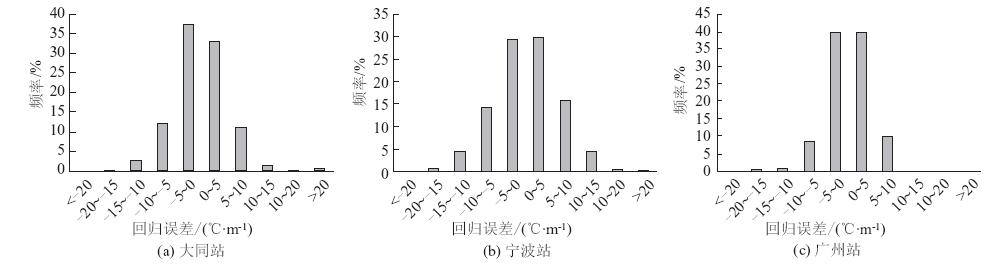
| 图 2 式(2)回归残差的频率分布图 Fig. 2 Frequency distributions of regression residuals of Equation (2) |
关于水泥混凝土路面温度梯度日最小值,即日最大负温度梯度的研究相对较少,但对于把握温度梯度日变化规律是十分关键的,是造成路面板角隅上翘和断裂的主要肇因。
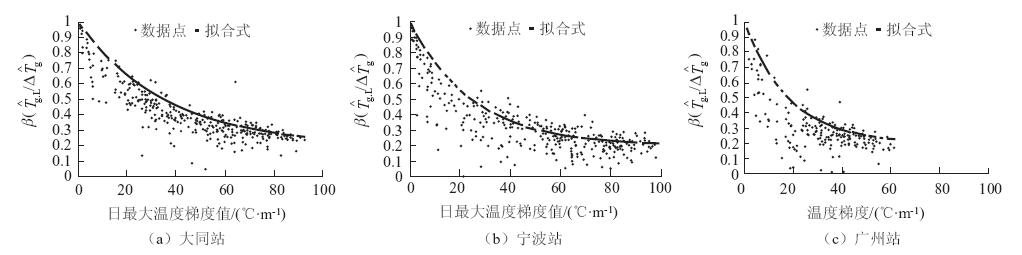
水泥混凝土路面温度梯度日最小值Tg.L的规律更为难寻。图 3给出大同、广州、宁波三地的标准厚度水泥混凝土路面温度梯度日最小值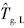 与路面温度梯度的日振幅
与路面温度梯度的日振幅 之比值
之比值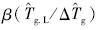 与日最大温度梯度
与日最大温度梯度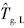 之间关系的散点。从图 3中可知,日最小温度梯度值与日温度梯度振幅之比β较为分散,但β的上限β-值与
之间关系的散点。从图 3中可知,日最小温度梯度值与日温度梯度振幅之比β较为分散,但β的上限β-值与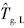 值之间具有良好的相关性,β值随着
值之间具有良好的相关性,β值随着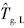 增大而减小。从应用上来说,把握β十分重要,在路面结构分析时,可将稍小的β值保守地用β替代。大同、广州、宁波三地的β-
增大而减小。从应用上来说,把握β十分重要,在路面结构分析时,可将稍小的β值保守地用β替代。大同、广州、宁波三地的β-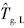 关系可统一表示为:
关系可统一表示为:
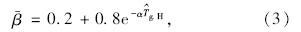
式中α为回归系数,大同取0.028、宁波取0.036、广州取0.070。
|
| 图 3 日最小温度梯度与温度梯度日振幅关系 Fig. 3 Relation between diurnal minimum temperature gradient and diurnal range of temperature gradient |
由β值定义和式(3),标准厚度的水泥混凝土路面日最小温度梯度上限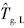 为:
为:

根据大同、宁波、广州三地为期1 a以上的路面温度实测数据以及气象数据,建立了二个标准厚度水泥混凝土路面温度梯度日最大值 的预估模型:第一个模型基于气象参数,以当日和前一日太阳日辐射量Q、气温日较差ΔTa为自变量;另一个以路表温度日最高、最低值Ts.max,Ts.min为模型自变量。这二个模型的预测精度较以往预估模型有着较显著的改善,其中,第2个模型的回归残差的标准差σ小于7 ℃/m。回归得到了标准厚度条件下,水泥混凝土路面温度梯度日最小值上限
的预估模型:第一个模型基于气象参数,以当日和前一日太阳日辐射量Q、气温日较差ΔTa为自变量;另一个以路表温度日最高、最低值Ts.max,Ts.min为模型自变量。这二个模型的预测精度较以往预估模型有着较显著的改善,其中,第2个模型的回归残差的标准差σ小于7 ℃/m。回归得到了标准厚度条件下,水泥混凝土路面温度梯度日最小值上限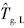 与日最大值
与日最大值 的关系方程。
的关系方程。
| [1] | 吴赣昌,黄国顺.自然条件下沥青路面结构的温度分布[J].佛山科学技术学院学报:自然科学版,1998(1):47-53.WU Gan-chang, HUANG Guo-shun. Temperature Distribution of Bituminous Pavement under Natural Climate Conditions[J]. Journal of Foshan University:Natural Science Edition, 1998(1):47-53. |
| [2] | 姚祖康. 铺面工程[M].上海:同济大学出版社,2006.YAO Zu-kang. Pavement Engineering[M]. Shanghai: Tongji University Press, 2006. |
| [3] | STINE W B, HARRIGAN P W. Solar Energy Fundamentals and Design with Computer Applications [M]. New York: John Wiley & Sons, 1985. |
| [4] | KELLEY E F. Application of the Results of Research to the Structural Design of Concrete Pavements [J].Journal Proceedings, 1939,35(6):437-464. |
| [5] | 谢国忠,袁宏,姚祖康.水泥混凝土路面最大温度梯度值[J].华东公路, 1982(6):9-20.XIE Guo-zhong, YUAN Hong, YAO Zu-kang. Maximum Temperature Gradient of Cement Concrete Pavement[J]. East China Highway,1982(6):9-20. |
| [6] | 刘荣辉,钱国平,郑健龙.周期性气候条件下沥青路面温度场计算方法研究[J].长沙交通学院学报,2002,18(2):71-75.LIU Rong-hui, QIAN Guo-ping, ZHENG Jian-long. Research on the Method for Calculating Temperature Field of Asphalt Pavement under the Condition of Recurrent Natural Environment[J].Journal of Changsha Communications University,2002,18(2):71-75. |
| [7] | 孙立军,秦健.沥青路面温度场的预估模型[J].同济大学学报:自然科学版,2006,34(4):480-483.SUN li-jun, QIN Jian. Prediction Model on Temperature Field in Asphalt Pavement[J]. Journal of Tongji University:Natural Science Edition,2006,34(4):480-483. |
| [8] | 胡晓,曹德洪,贾璐,等. 夏季桥面沥青铺装层温度预估及其力学影响[J].公路工程,2008,33(1):70-73.HU Xiao, CAO De-hong,JIA Lu, et al. Temperature Prediction for Asphalt Pavement on Bridge Decks in Summer and Related Mechanical Response[J]. Highway Engineering, 2008,33(1) :70-73. |
| [9] | 贾璐,孙立军,黄立葵,等. 沥青路面温度场数值预估模型[J]. 同济大学学报:自然科学版,2007,35(8):1039-1043.JIA Lu, SUN Li-jun, HUANG Li-kui, et al. A Numerical Temperature Prediction Model for Asphalt Concrete Pavement[J]. Journal of Tongji University:Natural Science Edition, 2007,35(8): 1039-1043. |
| [10] | 邹晓翎,谈至明,钱晨.路面结构层温度特征值的估计[J]. 同济大学学报:自然科学版,2012,40(7): 1041-1045.ZOU Xiao-ling, TAN Zhi-ming, QIAN Chen. Estimation of Characteristic Temperatures in Pavement Structure [J]. Journal of Tongji University:Natural Science Edition,2012,40(7): 1041-1045. |
| [11] | 谈至明,孙立军.路面结构低温状况分析[J].同济大学学报,1999,27(5): 520-525.TAN Zhi-ming, SUN Li-jun. Low Temperature Condition of Pavement Structure[J]. Journal of Tongji University:Natural Science Edition,1999,27(5):520-525. |
 2015, Vol. 31
2015, Vol. 31
