扩展功能
文章信息
- 邵财泉, 廖公云, 李植淮, 黄晓明, 李连友
- SHAO Cai-quan, LIAO Gong-yun, LI Zhi-huai, HUANG Xiao-ming, LI Lian-you
- 基于AASHTO 2002的我国沥青路面设计参数修正
- Revision of Design Parameters of Asphalt Pavement of China Based on AASHTO 2002
- 公路交通科技, 2015, Vol. 31 (1): 35-40
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (1): 35-40
- 10.3969/j.issn.1002-0268.2015.01.006
-
文章历史
- 收稿日期:2014-04-10
2. 中国路桥工程有限责任公司, 北京 100011
2. China Road and Bridge Corporation, Beijing 100011, China
AASHTO 2002沥青路面结构设计方法是世界上最具影响力的设计方法之一,该方法是在大量试验路段资料的基础上总结出来的一种力学-经验设计方法。我国现行沥青路面设计规范JTG D50—2006[1]与AASHTO 2002在设计参数上存在着较大差距。因此,很有必要借鉴AASHTO设计方法对设计参数的考虑,改善我国规范在设计参数上的不足。
目前,国内有不少学者研究美国AASHTO 2002设计方法。李刚[2]等结合阿尔及利亚东西高速公路路面设计项目,对AASHTO 2002设计方法、设计参数以及设计步骤作了详细介绍,为今后按照AASHTO方法进行路面设计提供参考。陈忠达等[3, 4, 5]考虑了不同季节轴载对沥青路面疲劳损坏的不同影响,提出了季节修正系数的概念,并给出了季节修正系数的建议值,从而完善了轴载换算理论,使轴载等效换算更加合理。武红娟[6]考虑到季节变化对土基回弹模量的影响, 参考AASHTO设计方法提出用等效回弹模量代替最不利季节模量作为土基强度设计值。王永胜[7]等主要通过材料模量等参数对AASHTO方法与我国沥青路面设计方法进行对比分析,研究发现我国材料静态参数与AASHTO设计方法动态参数有良好的对应关系。国内外不少学者[8, 9, 10]进行了沥青路面材料动、静态回弹模量的对比研究,系统研究了动态模量的影响因素,并给出了动静模量比的建议值。众所周知,沥青路面设计是综合交通量、材料参数和土基回弹模量等设计参数于一体的整体性设计,并不能独一而论。因此,本文将借鉴AASHTO设计,在前者研究基础上综合考虑材料动态模量,季节对交通轴载换算和土基回弹模量的影响,并进行实例分析。
1 设计资料
拟定一新建高速公路为双向四车道,拟采用沥青路面结构进行设计。该地区一年内不同季节的土基回弹模量值见表 1。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Ei/MPa | 121.3 | 118.4 | 40.1 | 46.3 | 50.6 | 70.8 | 69.7 | 68.4 | 69.2 | 73.2 | 57.2 | 125.4 |
该路段所在地区全年将被划分为3个季节段,其中3—5月为春融期,6—9月为雨季期,10月至次年2月为其他季节(包括冬季和初春),近期交通组成与交通量状况如表 2所示。交通量年平均增长率为7.1%。
| 季节段 | 黄海DD680 | 北京BJ130 | 东风EQ140 | 黄河JN360 | 小计 |
| 3—5月 | 150 | 123 | 143 | 64 | 480 |
| 6—9月 | 177 | 199 | 184 | 102 | 662 |
| 10—2月 | 219 | 226 | 212 | 110 | 767 |
| 合计 | 546 | 548 | 539 | 276 | 1 909 |
当量轴次是沥青路面结构设计的重要交通参数,并用累计当量轴次反映路面结构的疲劳性能。在我国规范中[1],当以设计弯沉值和沥青层层底拉应力为指标时,各级轴载均应按公式(1)换算成标准轴载P的当量轴次N:

众所周知,不同轴载对路面结构将产生不同的疲劳影响。然而,即使是相同的轴载,在不同季节对路面结构产生的疲劳损坏影响也是不同的。对此,AASHTO设计方法对于交通量不仅考虑了月份修正系数,甚至考虑到小时修正系数。因此,在进行轴载换算确定当量轴次时,应考虑轴载在不同季节对路面疲劳损坏的影响。
根据弹性层状体系理论,不同轴载作用下的弯沉与轴载的经验关系为:

式中,P1,P2为不同轴载对应的轴重;l1,l2为相应于轴载为P1,P2的实测轮隙回弹弯沉值;b为与路面结构有关的指数,平均值b=0.87。
季节修正系数α和季节影响系数K这二者之间的关系,可利用轴载换算的原则进行确定。季节影响系数是指不利季节与正常季节实际弯沉值的比值。设正常季节时,在轴载P作用下,路表弯沉值为l;不利季节时,在轴载P作用下,路表弯沉值则为l′,而l′=lK,相当于在正常季节时轴载P′(P′>P)的作用效果。由此,根据式(2)可知:

由此可知:

由此可见,不利季节轴载P的作用与正常季节轴载P′的作用对路面的损害是等效的。
根据轴载换算式(1)可知:

由式(5)知,季节修正系数α为季节影响系数K的5次方,可见α对轴载换算的影响很大。因此,轴载换算时很有必要考虑季节修正系数的影响。
因此,式(1)可修改为:

AASHTO中将全年分为不利季节(春季)、有利季节(冬季)和较有利季节(夏、秋季),本文根据该路段所在地区,将全年分为春融期(3—5月)、雨季(6—9月)和其他季节(冬季和初春,10月至次年2月)。
20世纪70年代前后,在全国范围内对季节影响系数K进行了广泛、全面的调查和试验,初步确定了各种状态、各种土质的季节影响系数,其值变化范围大致为K=1.05~2.00,一般K=1.1~1.4,与自然区划、干湿状态、土质等因素有关,由式(5)可知季节修正系数α=1.61~5.38。
根据AASHTO以及相关文献给出的建议值,同时结合该高速公路所在地区土质条件,本文选定季节修正系数α为4.0(春融期)、2.0(雨季)、1.0(其他季节)。经过计算,各季节原始的当量轴次以及季节修正后的当量轴次如表 3所示。
| 3—5月 | 6—9月 | 10—2月 | 合计 | |
| 原始当量轴次/次 | 409.4 | 583.1 | 659.0 | 1 651.5 |
| 季节修正系数α | 4.0 | 2.0 | 1.0 | |
| 季节修正后的当量轴次/次 | 1 637.6 | 1 166.2 | 659.0 | 3 462.8 |
从表 3可以看出,经过季节修正后的当量轴次为原始当量轴次的2.1倍。可见,季节修正系数对轴载换算的影响是很大的。利用修正后的当量轴次,再根据公式 ,可得到设计年限内一个车道的累计当量轴次为1.4×107次,属于重交通。而原始的累计当量轴次为6.9×106次,属于中等交通。对比可发现,经过季节修正后的交通等级从中等交通变为了重交通,这再次说明季节修正系数的不可忽视。
,可得到设计年限内一个车道的累计当量轴次为1.4×107次,属于重交通。而原始的累计当量轴次为6.9×106次,属于中等交通。对比可发现,经过季节修正后的交通等级从中等交通变为了重交通,这再次说明季节修正系数的不可忽视。
3 等效土基回弹模量的确定
AASHTO设计方法考虑了不同季节土基回弹模量的差异,采用有效土基回弹模量进行设计,相比于我国最不利季节土基回弹模量,采用有效土基回弹模量既保证了路面的整体结构强度,又减少了不必要的浪费,更具有合理性。因此,鉴于AASHTO的有效土基回弹模量,对我国设计方法提出等效回弹模量。
在我国规范中设计弯沉值按式(7)确定:

式中,ld为设计弯沉值(0.01 mm);Ac,As,Ab分别为公路等级系数、面层类型系数和路面结构类型系数。
路表计算弯沉值按式(8)确定:

式中,ls为路表计算弯沉值;F为弯沉综合修正系数;p,δ为标准车型的轮胎接地压强和当量圆半径;αc为理论弯沉系数。
令式(7)、式(8)相等可得:

用A代替AcAsAb,并将式(9)变化可得:
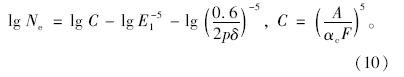
将p=0.7 MPa,δ=10.65 cm代入式(10)整理可得:

若NT为预期的总累计当量轴次,损伤率Dr为预期的和允许的累计当量轴次之比,可用下式表示:

假设NT在n个时期内均匀分布,累积损伤率为:

令式(12)与(13)相等,得:

式(14)即可确定用各个季节土基回弹模量E1i表示的等效土基回弹模量Ese。定义相对损伤uf为:

一年内不同时期(一个月或半个月)测定的季节路基土回弹模量E1i,按它们对路面服务能力的相对损伤程度,分别赋予相应的权系数uf,叠加各月的相对损伤,除以月数后求平均损伤,最后得到等效土基回弹模量Ese,见表 4。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| E1i/MPa | 121.3 | 118.4 | 40.1 | 46.3 | 50.6 | 70.8 | 69.7 | 68.4 | 69.2 | 73.2 | 57.2 | 125.4 |
| uf | 0.000 36 | 0.000 41 | 0.092 | 0.045 | 0.029 | 0.005 3 | 0.005 8 | 0.006 3 | 0.006 0 | 0.004 5 | 0.016 | 0.000 31 |
| xf=0.018 | Ese=55.53 MPa | |||||||||||
从表 4中可以看出,最不利季节土基回弹模量为40.1 MPa,而等效土基回弹模量为55.53 MPa。由于春融期较短,若采用最不利季节回弹模量势必会造成浪费,而等效土基回弹模量兼顾了各个季节对土基的影响,既保证结构安全,又更具合理性。
4 材料动态模量
众所周知,路面结构实际上受到来自车辆、气候等因素的不断变化的作用。它的实际工作状态无论是力学模型、材料的性质都与现行的静态力学体系有着较大的差距。
根据我国规范,沥青混合料的抗压回弹模量是在温度为20 ℃(层底弯拉应力计算时取15 ℃)时,用圆柱体试件在无侧限逐级加载卸载作用下测得,由于加载卸载速度慢,测得的是材料的静态模量。AASHTO设计方法采用重复荷载间接拉伸试验(ASTM D-4123)测得沥青混合料的动态回弹模量。
研究表明,动态模量与温度大小、荷载频率和荷载大小有关。一般认为荷载频率为10 Hz时,大致相当于汽车行驶速度70 km/h,而根据已有文献的研究可知,当荷载频率大于10 Hz时,动态模量的增加趋于平缓,与静态模量大小的比值基本不变。因此,本文选用温度为20 ℃、频率为10 Hz、荷载大小为0.7 MPa时的动态模量(层底弯拉应力计算时取15 ℃)。
大量文献[8, 9, 10]依照ASTM D-4123的试验方法,进行了沥青混合料动、静态回弹模量的对比研究,并认为15 ℃时动静模量比为1.3~1.7,20 ℃ 时动静模量比为1.7~2.5。
半刚性基层材料是我国高等级公路广泛使用的基层材料。国内不少学者[11, 12, 13]经过研究给出了我国的半刚性材料模量与AASHTO推荐模量之间的关系,由于该对比试验是依据AASHTO设计方法中材料模量试验方法得到的,所以能够反映两种设计模量的关系。对于90%概率水平时,动态模量比静态模量大400 MPa。
因此,对于沥青混合料,选取15 ℃时动静模量比为1.5,20 ℃时动静模量比为2。对于半刚性基层材料,选取动态模量比静态模量大400 MPa。材料静态与动态模量值如表 5所示。
| 静态模量 | 动态模量 | |||
| E20 ℃ | E15 ℃ | Ed20 ℃ | Ed15 ℃ | |
| 细粒式沥青混凝土 | 1 200 | 1 800 | 2 400 | 2 700 |
| 中粒式沥青混凝土 | 1 000 | 1 600 | 2 000 | 2 400 |
| 粗粒式沥青混凝土 | 800 | 1 400 | 1 600 | 2 100 |
| 水泥稳定碎石 | 1 500 | 3 000 | 1 900 | 3 400 |
| 水泥石灰砂砾土 | 1 000 | 1 700 | 1 400 | 2 100 |
以第1节中给出的设计资料为依据,结合轴载换算的季节修正系数、等效土基回弹模量和材料动态模量,利用HPDS沥青路面设计软件分别进行以下5种结构设计,对于这5种结构设计保持面层和基层厚度不变,以底基层为设计层,所用的结构设计图如图 1所示。

|
| 图 1 路面设计结构图 Fig. 1 Designed pavement structure |
(1)原始结构设计(结构1):根据第1节所给原始资料进行结构设计;
(2)轴载换算季节修正结构设计(结构2):只对原始数据中的交通轴载换算进行季节修正,保持其余参数不变进行结构设计;
(3)等效土基回弹模量结构设计(结构3):只改变原始数据中最不利季节土基回弹模量,采用有效土基回弹模量,保持其余参数不变进行结构设计;
(4)材料动态模量结构设计(结构4):只改变原始数据中的材料静态模量,采用动态模量进行结构设计;
(5)综合结构设计(结构5):对原始数据中的轴载换算进行季节修正,同时采用有效土基回弹模量、材料动态参数进行结构设计。
各结构设计结果如表 6、图 2所示。
| 结构 | 累计当量轴次/次 | 土基回弹模量/MPa | 材料模量 | 底基层理论厚度/cm | 底基层设计厚度/cm |
| 1 | 6.9×106 | 40.1 | 静态 | 16.9 | 17 |
| 2 | 1.4×107 | 40.1 | 静态 | 17.3 | 18 |
| 3 | 6.9×106 | 55.53 | 静态 | 13.8 | 15 |
| 4 | 6.9×106 | 40.1 | 动态 | 18.1 | 19 |
| 5 | 1.4×107 | 55.53 | 动态 | 15.2 | 16 |

|
| 图 2 各结构底基层厚度对比 Fig. 2 Comparison of subbase thicknesses of different structures |
从图 2可以发现,轴载换算季节修正后(结构2)的底基层设计厚度(18 cm)与采用材料动态模量设计(结构4)的底基层设计厚度(19 cm)分别比原始结构(结构1)底基层厚度(17 cm)大1 cm、2 cm,而采用等效土基回弹模量设计(结构3)的底基层厚度(15 cm)比原始结构(结构1)底基层厚度(17 cm)小2 cm。可以发现,这些因素都影响底基层设计厚度的变化,说明在路面设计时若仅考虑某一因素(轴载换算的季节修正系数、等效土基回弹模量、材料动态模量)的影响,势必会造成路面结构设计的不合理。但是,若像结构5一样综合考虑3个因素进行路面结构设计,便能有效避免上述情况的发生,使设计结构既能满足路面结构性能要求,又能在一定程度上减少不必要的浪费,经济又合理。
6 结论
(1)虽然高速公路、一级公路、二级公路的设计速度不同,但并不影响轴载换算和土基回弹模量。且设计速度变化范围为60~120 km/h时,对应的荷载频率为10~15 Hz,在此频率范围内,动态模量与静态模量比值的变化范围基本不变。因此本文对设计参数的分析结果同样适用于其他等级的道路。
(2)不同季节交通轴载对路面结构影响差异较大,季节修正前后的累计轴载差异也较大,考虑轴载换算的季节修正系数更符合实际情况。
(3)不同季节的土基回弹模量值差异较大,选用等效土基回弹模量更能体现季节对土基回弹模量的影响,使路面结构设计更具合理性。
(4)材料动态模量与静态模量之间存在差异,选用动态模量更能贴合车辆——道路实际作用状态。
(5)将上述因素综合考虑后的路面结构既能满足路面结构性能要求,又能减少不必要的浪费,更具经济性与合理性。
| [1] | JTG D50—2006, 公路沥青路面设计规范[S].JTG D50—2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [2] | 李刚, 张留俊, 丁小军. 基于AASHTO的沥青混凝土路面设计方法[J]. 公路,2008(9): 143-147.LI Gang, ZHANG Liu-jun, DING Xiao-jun. Asphalt Concrete Pavement Design Method Based on AASHTO[J]. Highway, 2008(9): 143-147. |
| [3] | 陈忠达, 武建民, 冯明硕, 等. 沥青路面轴载换算季节修正系数[J]. 长安大学学报: 自然科学版, 2003, 23(6): 1-3.CHEN Zhong-da, WU Jian-min, FENG Ming-shuo, et al. Season-correcting Coefficient of Axle Load Conversion for Asphalt Pavement[J]. Journal of Chang'an University: Natural Science Edition, 2003, 23(6): 1-3. |
| [4] | 孙志林, 黄晓明. 基于路基顶面压应变的沥青路面轴载换算方法[J]. 公路交通科技, 2007, 24(7): 28-30.SUN Zhi-lin, HUANG Xiao-ming. Conversion Method of Axle Load for Asphalt Pavement Based on Compression Strain on Top of Subgrade[J]. Journal of Highway and Transportation Research and Development, 2007, 24(7): 28-30. |
| [5] | 孟书涛, 徐建伟. 轴载、轮胎内压与轴载换算的研究[J]. 公路交通科技, 2004, 21(6): 4-7.MENG Shu-tao, XU Jian-wei. Research on Axle Load Equivalency with Load and Tire Pressure[J]. Journal of Highway and Transportation Research and Development, 2004, 21(6): 4-7. |
| [6] | 武红娟, 王选仓. AASHTO法中土基模量取值对沥青路面的影响[J]. 长安大学学报: 自然科学版, 2008, 28(5): 14-17.WU Hong-juan, WANG Xuan-cang. Influence of Design Value of Soil Base's Modulus in AASHTO on Asphalt Pavement Design[J]. Journal of Chang'an University: Natural Science Edition, 2008, 28(5): 14-17. |
| [7] | 王永胜, 孔永健. AASHTO沥青路面结构设计方法在我国的适用性研究[J]. 北方交通大学学报, 2004, 28(4): 58-62.WANG Yong-sheng, KONG Yong-jian. Research on the Applicability of AASHTO Asphalt Pavement Structure Design Method in China[J]. Journal of Northern Jiaotong University, 2004, 28(4): 58-62. |
| [8] | 孙建. 沥青混合料动态模量研究[D]. 西安: 长安大学,2007.SUN Jian. Research of Asphalt Mixture Dynamic Modulus[D]. Xi'an: Chang'an University, 2007. |
| [9] | 王旭东. 沥青路面材料动力特性与动态参数[M]. 南京: 东南大学, 1998.WANG Xu-dong. Research of Asphalt Pavement Material Dynamic Characteristics and Parameters[M]. Nanjing: Southeast University, 1998. |
| [10] | 羊明. 沥青混合料动态模量研究[D]. 长沙: 长沙理工大学, 2007.YANG Ming. Research on the Dynamic Modulus of Asphalt Mixtures[D]. Changsha: Changsha University of Science & Technology, 2007. |
| [11] | 郭大进, 王旭东. 水泥土动态模量试验的分析[J]. 公路交通科技, 2000,17(5): 18-20.GUO Da-jin, WANG Xu-dong. Analysis of Dynamic Modulus Testing of Cement-soils[J]. Journal of Highway and Transportation Research and Development, 2000,17(5): 18-20. |
| [12] | WITCZAK M W, BARI J. Development of a Master Curve (E*) Database for Lime Modified Asphaltic Mixtures [R]. Tempe, Arizona: Arizona State University, 2004. |
| [13] | CLYNE T R, LI X, MARASTEANU M O, et al. Dynamic and Resilient Modulus of Mn/DOT Asphalt Mixtures, MN/RC-2003-09[R]. Washington, D. C.: Transportation Research Board, 2003. |
 2015, Vol. 31
2015, Vol. 31
