扩展功能
文章信息
- 宣登殿, 杨新征
- XUAN Deng-dian, YANG Xin-zheng
- 现代仓储系统货物入库分配优化模型及算法研究
- Study on Optimization Model and Algorithm of Storage Allocation in Modern Warehouse System
- 公路交通科技, 2014, Vol. 31 (12): 153-158
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 153-158
- 10.3969/j.issn.1002-0268.2014.12.024
-
文章历史
- 收稿日期:2014-05-20
2. 交通运输部科学研究院, 北京 100029
2. China Academy of Transportation Sciences, Beijing 100029, China
仓储系统是现代物流系统的重要组成部分,不仅能够有效调节整个物流系统的平衡,产生时间价值,而且能够促进生产企业的生产和销售从而提高企业的生产效益[1, 2, 3]。在现代仓储系统中,一方面货物的种类更加繁多,另一方面仓库的构造特别是货架的构成也更复杂,这些都导致了货物的出入库操作工作量急剧增大。对于现代仓储系统,货物的存取率是衡量系统运作的重要指标,而货物的存取率又在很大程度上取决于货位的优化分配,因为货位的优化分配能方便拆垛和堆垛,方便盘库和移库,从而大大提高出入库效率。国外学者在仓库分区中提出了黄金区域的概念,利用连续数学模型对仓库空间进行了最优分区,并对仓储过程中的再分配策略进行了改进,减少了货物拣选时间[4, 5, 6]。目前,我国很多企业仓库货位编码依旧采用传统按层或者按列进行顺序编码,几乎没有任何优化措施,传统的优化方法是按照出入库的频率将货物分为A,B,C三类,这种编码方式对仓库管理人员来说简单直观,而且方便查找,缺点是由于按照顺序在某行或者某列编码虽然连续,但遇到换行或换列可能会出现阶跃点从而导致堆垛机增加运行路径,而且货架越长或者高度越高,这种不利因素也就越明显[7, 8]。为降低仓储系统的运行成本并提升货物的入库效率,货位编码应尽量靠近入库点。堆垛机进行拣选作业尽量优先考虑低层或靠近出入库点处的货物来减少堆垛机的耗能,从而降低运行成本。该编码方式也没有考虑到货架的承重能力及稳定性的要求。同一货架上不同的货物可能在质量和出入库频率等方面存在很大区别,在考虑货物出入库频率的因素来确定靠近入库工作中区域的同时也要考虑货架中心的稳定性,质量较大的货物应处于货架底层。货物的货位合理分配能减少出入库时间、提高堆垛机设备效率以及减少倒库作业[9]。同时,货位的优化分配是一个处于动态的过程,由于货物的频繁出入库操作使货物出入库口货物存放过于集中,导致货物重心偏离,使货架不稳,同时货物的出入库频率有可能受到外界条件的刺激而发生改变,当货架货物存取率发生变化或质量发生变化的时候需进行重新分配,保证仓储系统的运作效率及货架的稳定性。 1 问题和模型
对于现代仓储系统,其主要设施必然是自动化立体仓库。货物入库前,首先要对其进库后的区域即货架,进行分区,分区完毕后进行货物的具体货位分配。分区时假设:货物的存取率已知、货物的存放数量已知、货物的种类已知和单个货物质量已知。这里,货区划分方法如下:
(1)按照货物的出入库频率和质量对货区进行分类,货物种类的数目和仓库货架分区的数量相同。
(2)按照货物的分类数将仓库货架分为扇形。例如一个8列4层的货架分为4个货区,对货物建立关于频率和质量的多目标函数,最终将货物分为n类,用p表示货物质量和出入库频率权重组合,p=0,1,2,…,n分别表示货物质量和出入库频率组合权重逐渐减小。按照p值的大小不同将货区进行分类。在表 1中p值相同的货物放在同一区域内,并且按照p值的大小进行排序,p值越小越接近出入库口。
| p=3 | p=3 | p=3 | p=3 | p=3 | p=3 | p=3 | p=3 |
| p=2 | p=2 | p=2 | p=2 | p=2 | p=2 | p=3 | p=3 |
| p=1 | p=1 | p=1 | p=1 | p=2 | p=2 | p=3 | p=3 |
| p=0 | p=0 | p=1 | p=1 | p=2 | p=2 | p=3 | p=3 |
(3)上步骤中可能有的分区并不能满足货位数的需求,则按照就近原则进行处理,就近取多补少,如果货区位置不够可以从相邻的货位进行存取货。
货位分配是在货区分配的基础上进行的,首先对货架货区按货物种类进行扇形区域划分,基于货架分区进行货位的优化分配,然后使用货位优化策略来对货架上的货位进行优化管理。自动化立体仓库货位分配的主要目标是在进行出入库操作时能按照最优选择进行存放或拣取,提高自动化立体仓库的作业效率[8, 9]。
假设建立数学模型如下:某仓库固定货架共有p列q层,处于第i列j层的货位记为(i,j)(i=1,2,…,p; j=1,2,…,q),出入库口位置记为(0,0),货架主要的权重因素设为货物重量和出入库频率,则对该多目标问题所建立目标函数如下:
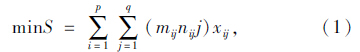
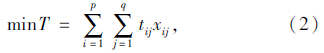

上述模型中,式(1)依据上文中的货位分配策略中上轻下重的策略,即货物在进行入库操作时重的货物放在底部,轻的货物放在上部,使整个货架的重心靠近底部,保证货架的稳定性。式(2)依据货位分配中最短路线策略,入库的货物由堆垛机寻找到按货物频率等级分区的位置,然后存放于离出入库口最近的货位上。式(3)为在不考虑堆垛机的加速度的情况下,将第i列j层货位上的货物由堆垛机进行拣选作业运送到出入库口处所需要的时间。 2 算法构建
遗传算法基于理论问题和生物群体的相似性分析,通过编码操作建立二者之间的关联,然后通过模仿自然界中生物遗传与进化机理,设立了选择、交叉和变异等操作,来完成对问题最优解的搜索寻优过程,最后通过一定的最优判定准则来终止问题计算[10, 11, 12]。
货位的分配需同时考虑货架稳定性和出入库效率,这是一个多个目标函数的优化问题。本文运用基本遗传算法求解。基本遗传算法包括3个算子:选择、交叉、变异。其主要步骤程如下:
(1)对整体货架采用从上而下,从左到右的方式进行矩阵编码,从而得到整个货区的编码。根据货位的特点,采用q×p矩阵对解进行编码,如果矩阵的第i行j列位置的元素为m,则表示编号为m的货物放在货架的第i层j列上。
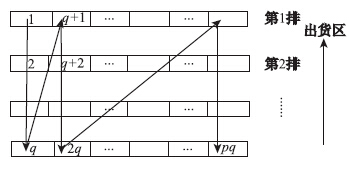
图 1为第1层货架的编码示意图,以后每层的编码方式与第1层货架相同,且第2层货架的编码起始数字为q+1。矩阵编码方式为一对一进行编码,矩阵中每个元素都代表一个货位:1,2,3,…,q,q+1,q+2,…,2q,2q+1,…,3q…,4q,…,pq。
|
| 图 1 货架的编码示意图 Fig. 1 Schematic diagram of shelf code |
例如取一3行4列仓库,编号如下:
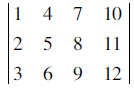
(2)将货架分为N个货区,对N个货区进行分配编号,即C1,C2,C3,C4,…,CN,整体货区编号为:C=C1,C2,C3,C4,…,CN。
按上述3行4列仓库为例:设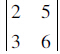 为第一区域货区C1,则其对应货架编号为:[2, 3, 5, 6];剩下其余部分为第二区域C2,则对应编码为:[1, 4, 7, 8, 9, 10, 11, 12]。
为第一区域货区C1,则其对应货架编号为:[2, 3, 5, 6];剩下其余部分为第二区域C2,则对应编码为:[1, 4, 7, 8, 9, 10, 11, 12]。
(3)每个货区对应编号为:H1,H2,H3,H4,…,HN,统一合成完整编号为:H=[H1,H2,H3,H4,…,HN]。
假设1区要放入2件货物,2区需要放入3件货物。
解码:编码X1中的1,2并非原货架编号1,2,而是对应货区编号H1中的[1, 2],即原仓库货架编号的C1 [2, 3]。同理X2中[2, 4, 5]也并非原货架编码,而是对应的区域编号H2中的[2, 4, 5],即仓库货架编码C2 [4, 8, 9]。
(4)利用X=X1,X2,X3,X4,…,XN和C=C1,C2,C3,C4,…,CN可以得到货物存放货位的实际位置,记录货物实际位置编码为:y,y1=C1(X1),y2=C2(X2),y3=C3(X3),y4=C4(X4),…,yN=CN(XN)。 在真实处按照货物所在区域进行标注,例如y1表示1区,则存放货物的位置用1表示,无货物则用0表示;其他同理。最终得到关于货物存放的矩阵,由数字0,1,2,3,4,5组成。其中yN=HN(XN)所代表含义为:利用货区内部编码对应货架位置编码,从而得到实际货物存放位置,如例中Y1和Y2所对应的货物存放地点为:
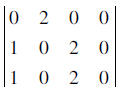
(5)适应度函数的选择:

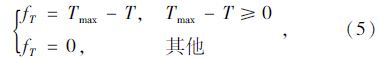
(6)本文中将采用联赛选择方式进行选择操作,对两个目标函数分别从上代的群体中以等概率选取N个染色体,并对其适应值进行排序,选择适应值最大的染色体进行提取,随后继续按照上述方法进行操作,直到重新构成N个染色体,形成一个新的群体。为了保证两个子目标函数的统一性,需分别对其进行标注,例如S,T,表示两个个体分别代表的子目标函数为货架的稳定性和货物的进出库时间。
(7)交叉操作。交叉操作用于组合出新的个体,在解空间中进行有效的搜索,同时降低有效模式的破坏概率。本文采用部分匹配交叉策略,为防止某个体形成仅在某一方面性能较好的物种,引入了交配限制策略,只有当两个个体标签不同时,才能进行交叉操作。通过这种方式,各个子目标函数之间优良的基因可以得到充分的交叉优化组合,从而产生性能更好的优化解。货位的分配问题主要考虑的是对货位进行顺序的优化,目标函数的结果能直接将货物在货架上的位置表现出来[3, 4, 5, 6, 7]。由于矩阵中不能出现相同编码,否则表达出现歧义,在编程中由于矩阵采用序号编码,故交叉策略为找出需要交叉的两部分编码,然后将其不同的部分挑出,进行打乱重排,再分为相同的两个部分,分别和前面两个相同部分进行组合,形成交叉后的编码。
例如有两个个体标签不同的X2进行交叉操作,分别用S2和T2进行表示,S2=[1, 2, 4],T2=[2, 5, 6],交叉的时候取出相同部分2,剩余的部分打包在一起[1, 4, 5, 6],打乱顺序[1, 6, 4, 5],然后分成两部分再加上各个部分相同的部分2,形成新的S2′和T2′,S2′=[1, 2, 6],T2′=[2, 4, 5],完成交叉操作。
(8)变异操作,同交叉操作不能出现相同编码,所以在进行变异选择时,可以随机选取n个编码,在选取这n个编码之外再选取n个编码,然后将后选取的n个编码替换掉原来的n个编码,这样就形成了变异操作,同时保证了编码的各异性。本文中变异操作为互换算子,即随机交换染色体中两个不同基因编码的位置,即两个货位上的货物进行对换,属于小范围变异。如果在货架上随机选择一个矩形的区域,然后对区域中的物品进行倒置操作,属于大范围变异。
在上述3层4列货架案例中,假设有个X2=[2, 4, 5],其中随机取1位变异,假设选取了中间1个,就是4需要变异。
(9)货架上会有预留一定数量的空位或某些货位上的数量为0,按照稳定性和最大存取效率的要求应将这些空位排到货架顶层或者出库台最远的货位上,因此每次进行交叉变异后该对矩阵进行一次修补操作,如果有空位则货物应向下移动,将空位安排到货架顶层。
(10)为保证计算结果最优,防止失去最优解,需在变异后增加随机解到群体,因为交叉或者变异可能导致最优解的丢失。
通常算法的终止条件有两种:(1)事先给定一个最大迭代次数。(2)判断最优值是否趋于一个稳定值,连续若干次迭代没有发生变化,由于迭代若干次后种群的个体字符结构都趋于相似,所以即使继续执行也很难发现更好的解。本文终止条件为如果群体标准偏差小于一定的值,则认为群体收敛。种群标准差定义如下:
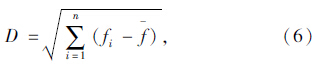
3 案例计算
某自动化立体仓库设备参数为:
堆垛机水平运行速度:3 m/s;托盘货位高:1050 mm;堆垛机垂直运行速度:1 m/s;货架层数:12;托盘货位长:1300 mm;货架列数:40;托盘货位宽:1100 mm;托盘型号:(1000×800)mm。
存放货物具体参数见表 2。
| 货位编号 | 占货位数/个 | 作业概率/% | 每个货物质量/kg |
| 1 | 90 | 32 | 50 |
| 2 | 80 | 15 | 70 |
| 3 | 85 | 28 | 100 |
| 4 | 40 | 10 | 40 |
| 5 | 70 | 15 | 80 |
现按要求对200个货物进行入库操作,其中1类和3类货物各60个,2类和4类货物各20个,5类货物40个。
首先根据货位优化策略需将货架划分为和货物种类相同的扇形区域,根据p的大小最终确定货物所在的位置,计算所得结果为:A区货物编号为3;B区货物编号为1;C区货物编号为5;D区货物编号为2;E区货物编号为4。然后根据货物所占货位格数确定货架分区的扇形区域,如果图 2中分区并不能满足货物所占货位个数,则相邻两个区域共占某些货位。

|
| 图 2 货区分布图 Fig. 2 Distribution of goods areas |
经过求解,所得结果如表 3和表 4所示。其中,矩阵中数字1,2,3,4,5代表所在区域A,B,C,D,E,并且存有货物,数字在矩阵中的位置代表货物在实际货架中的位置,数字0表示此处为空置货位。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | |
| 12 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 4 | 0 | 0 | 4 | 4 | 4 | 0 | 0 | 0 | 4 | 4 | 4 | 0 | 4 | 0 | 4 | 0 | 4 | 4 | 4 | 0 |
| 10 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 9 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 4 | 0 | 0 | 4 | 0 | 4 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 6 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 5 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 4 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 3 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 2 | 1 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 0 | 0 | 0 | 4 | 0 | 5 |
| 1 | 1 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 0 | 0 | 4 | 4 | 0 | 5 |
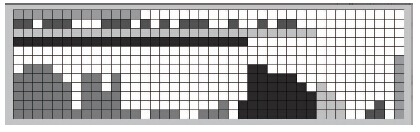
图 3中阴影部分表示存放货物入库情况,颜色由深到浅分别表示货位编号为1,2,3,4,5的5种货物。
|
| 图 3 各类货物入库存放位置 Fig. 3 Warehousing storage locations of various goods |
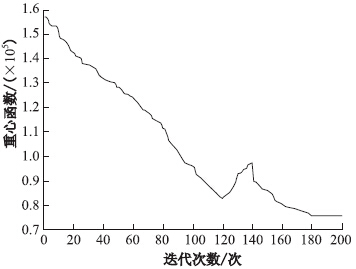
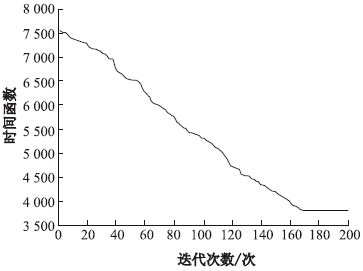
结果输出重心函数和时间函数(出入库总时间)的变化曲线,如图 4、图 5所示。
|
| 图 4 重心函数值变化曲线 Fig. 4 Curve of gravity center function |
|
| 图 5 时间函数值变化曲线 Fig. 5 Curve of time function |
通过图 4、图 5可以看出时间函数和重心函数随迭代次数的增加下降,当到达200次的时候已经收敛,重心函数由原来的1.58×105,迭代完成时降低到7.48×104;时间函数由原来的7 500,迭代完成后降低到3 788。由此可以看出经过货位优化,货物的出入库时间和货架重心都得到优化。 4 结论
针对现代仓储系统中的货物入库问题,本文首先将其分解为货区划分和货位分配两个连续的过程,接着介绍了货位优化准则以及货区划分方法,并建立了货位优化的数学模型,重点介绍了货位优化数学模型的建立过程以及模型建立后的算法设计和求解过程。最后,针对具体案例,在Matlab中进行了求解,得出入库货物的最优货位分配方案。
| [1] | 周晓,张锦,刘思婧,等. 基于变权的随机流量物流网络货流分配方法[J].公路交通科技,2012,29 (7):144-150.ZHOU Xiao,ZHANG Jin,LIU Si-jing,et al. A Method for Freight Flow Allocation in Stochastic-flow Logistics Network Based on Variable Weights[J]. Journal of Highway and Transportation Research and Development,2012,29 (7): 144-150. |
| [2] | 白世贞,刘莉.现代仓储物流技术与装备[M].北京:中国物资出版社,2007.BAI Shi-zhen,LIU Li. Modern Storage Logistics Technology and Equipment[M].Beijing:China Supplies Press,2007. |
| [3] | 叶怀珍. 物流工程学[M].北京:机械工业出版社,2008.YE Huai-zhen. Logistics Engineering[M]. Beijing:Machinery Industry Press,2008. |
| [4] | KOFLER M,BEHAM A,VONOLFEN S,et al. Modelling and Optimizing Storage Assignment in a Steel Slab Yard [C]// Proceedings of the 4th IEEE International Symposium on Logistics and Industrial Informatics. Slovakia:IEEE,2011,77-82. |
| [5] | MISEVICIUS A. An Implementation of the Iterated Tabu Search Algorithm for the Quadratic Assignment Problem [J]. |
| [6] | RAO S S,ADIL G K. A Mathematical Model for Optimal Partitions of Warehouse Storage Space Based on Turnover Density [C]// Proceedings of the 5th Asia Modelling Symposium. Manila: IEEE,2011:133-137. |
| [7] | 刘峰,施展,刘莹. 自动化立体仓库的货位分配模糊算法研究[J].上海理工大学学报,2011,33(11):71-74.LIU Feng,SHI Zhan,LIU Ying. Location Assignment Algorithm for AS/RS Based on Fuzzy Mathematics[J].Journal of University of Shanghai for Science and Technology,2011,33 (11):71-74. |
| [8] | 张晓兰,蒋丽娜,于洪涛.基于遗传算法的立体仓库货位动态分配优化[J]. 哈尔滨商业大学学报:自然科学版,2012,28 (1):66-67.ZHANG Xiao-lan,JIANG Li-na,YU Hong-tao. Research on Dynamic Location Assignment Optimization of Stereoscopic Warehouse Based on Genetic Algorithm[J]. Journal of Harbin University of Commerce:Natural Sciences Edition,2012,28 (1):66-67. |
| [9] | 邓爱民,蔡佳,毛浪.基于时间的自动化立体仓库货位优化模型研究[J].中国管理科学,2013,21 (6):107-112.DENG Ai-min,CAI Jia,MAO Lang. Research on Slotting Optimization in Automated Warehouse Based on Time[J]. Chinese Journal of Management Science,2013,21 (6):107-112. |
| [10] | 陈月婷,何芳. 基于遗传算法的自动化立体仓库的货位优化分配[J].物流科技,2008(1):38-41.CHEN Yue-ting,HE Fang. Location Assignment Optimization of AS/RS Based on Genetic Algorithm[J]. Logistics Sci-Tech,2008(1):38-41. |
| [11] | 马永杰,蒋兆远,杨志民. 基于遗传算法的自动化仓库的动态货位分配[J]. 西南交通大学学报,2008,43(3):415-421.MA Yong-jie,JIANG Zhao-yuan,YANG Zhi-min. Dynamic Location Assignment of AS/RS Based on Genetic Algorithm[J]. Journal of Southwest Jiaotong University,2008,43(3): 415-421. |
| [12] | LI M,TANG H. An Improved Genetic Algorithm for Locations Allocation Optimization Problem of Automated Warehouse [J]. Fuzzy Information and Engineering,2009,2(62):1549-1560. |
 2014, Vol. 31
2014, Vol. 31
