扩展功能
文章信息
- 戢晓峰, 普永明, 梁斐雯, 覃文文
- JI Xiao-feng, PU Yong-ming, LIANG Fei-wen, QIN Wen-wen
- 交通管制时限条件下城市物流配送优化双层规划模型
- Bi-level Programming Model for City Logistics Distribution Optimization under Time Restrict Condition Caused by Traffic Control
- 公路交通科技, 2014, Vol. 31 (12): 145-152
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 145-152
- 10.3969/j.issn.1002-0268.2014.12.023
-
文章历史
- 收稿日期:2014-04-17
2. 中山大学 地理科学与规划学院, 广东 广州 510275;
3. 同济大学 道路与交通工程教育部重点实验室, 上海 201804
2. School of Geography and Planning, Sun Yat-Sen University, Guangzhou Guangdong 510275, China;
3. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China
随着近年来电子商务的飞速发展和企业减少库存、提高服务水平的需要,城市物流配送正由传统配送向家庭配送和直接配送进行转变,并呈现出多品种、多批次、少批量的准时配送发展趋势。为顾客提供及时、满意的配送服务成为城市物流配送系统必须解决的关键问题,但是大量物流配送车辆加剧了城市交通拥堵。为了缓解物流配送车辆对交通拥挤的影响,城市管理者开始对驶入城区的物流配送车辆实行交通管制政策。对于城市物流配送公司而言,在有时间窗的交通管制情形下满足配送需求,需要均衡考虑环境成本、配送成本、配送服务质量等各方面的因素,要求保障企业收益的同时,为顾客提供及时准确的配送服务。为此,城市物流配送问题日益严峻,已成为交通和物流管理者关注的焦点。如何在特殊条件下对城市物流配送进行优化与均衡分析,国内外学者进行了初步探讨,如邓爱民[1]等分析了城市物流配送系统的内涵、组成、功能及优化目标,提出了城市物流配送系统优化的研究框架、基本方法与实现步骤;李作秋[2]等将路网中节点以货车的容量为约束进行分组,利用C-W节约算法寻求最优路线;戢晓峰[3,4,5]等从高强度快递需求区域移动仓库选址问题入手,在探究物流信息搜寻模式的基础上,分析了物流信息搜寻行为影响因素及物流信息组织模式,并在满足物流配送时效性约束的前提下,求解并优化了物流配送路线,为交通管制时限条件下的城市物流配送提供理论基础;罗雅婷[6]等利用博弈论对城市物流配送及城市交通组织进行博弈分析,剖析城市物流配送与城市交通组织直接的相互影响关系;魏航[7]通过对时变条件下有宵禁限制并有到达时间限制的最短路进行研究,证明了时变条件下有宵禁限制最短路的最优条件,并分析了宵禁对于获得最短路的影响;卢冰原[8]等针对城市物流配送中有时间窗多车型问题,构造出一种具有较高精度的提前-惩罚函数,建立具有模糊时间约束的多车型车辆调度问题;胡云超[10]等在分析城市货运交通管制条件下城市配送优化问题的主要因素和问题界定的基础上,综合考虑社会效益与环境污染,以城市物流配送综合效益为目标,构建了城市配送优化模型。
综上所述,大多数相关研究从微观角度对城市物流配送路径优化进行初步研究,提供了具有理论价值的成果,但是鲜少从城市的宏观角度针对时限条件下的城市物流配送优化进行探讨,缺乏相应的城市物流配送优化模型。交通管制时限条件下的城市物流配送优化研究能够有效缓解物流配送与城市交通的冲突,有利提升城市物流配送效率,提高物流配送企业经济效益。因此,本文对时限条件下的城市物流配送问题进行描述,综合考虑配送企业的配送成本、环境成本及配送时间,构建双层规划模型,以配送企业广义费用最小化作为上层模型,用于研究时限条件下的城市物流配送优化方案;下层模型为城市交通均衡分配模型,用于研究上层给出的城市物流配送优化方案中用户交通选择行为。采用遗传算法求解模型,以简单网络进行算例分析,并对比测算企业配送广义费用在交通管制时限情景与包含交通管制和用户时间窗的时限情景下的差异。
1 问题描述
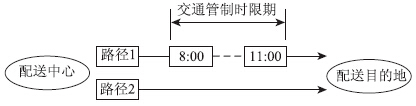
交通管制时限条件下城市物流配送问题实际上是如何在交通管制时限约束下,确定配送车辆的行驶路线,使配送车辆依照最短的行驶路径或最短的时间费用,降低城市环境污染并实现配送企业广义费用最小。时限条件下城市物流配送问题可以描述为:在配送网络G=(E,A)中,E为网络节点e(e=1,2,…,n)的集合,网络节点e为配送路径途经的道路交叉口,e∈E;A为网络节点间有向路段a(a=1,2,…,n)的集合,路段a为配送路径途径的道路,a∈A。配送中心为起点O,配送目的地为终点D,OD之间存在配送路径r(r=1,2,…,n),配送路径r由路段a组成;S为配送企业广义费用,其中S1为配送时间,S2为环境成本,S3为配送成本;令Z表示交通管制时限时间段z(z=1,2,…,n)的集合,z∈Z。求在交通管制时限下,由配送中心将货物配送至用户的过程中,最小的配送企业广义费用。交通管制时限条件下的城市物流配送过程,如图1所示,配送中心与配送目的地之间,存在一条路径上设置了交通管制时限。
|
| 图1 配送中心与配送目的地之间的有效路径 Fig.1 Effective paths between distribution center and distribution destination |
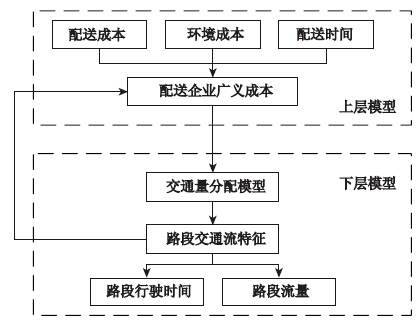
考虑到时限条件下的城市物流配送与优化模型问题是一个特殊的优化问题,本文构建时限条件下的城市物流配送双层优化模型,分析时间窗的存在对城市物流配送的影响程度,从而改善配送企业的广义费用,如图2所示。在物流配送中配送成本、环境成本与配送时间是配送企业广义成本的主要构成,因此,在上层模型引入配送成本、环境成本与配送时间刻画配送企业的广义成本。下层模型主要描述驾驶员的路径选择行为,本文基于随机用户平衡思想,将各路径的行驶时间之和最小作为优化目标进行交通分配,并通过将交通分配的最终结果反馈给上层模型实现循环求解。
|
| 图2 时限条件下城市物流配送优化模型结构 Fig.2 Optimization model structure of city logistics distribution under time restraint condition |
在时限条件下的城市物流配送的优化模型与均衡分析中,考虑影响配送企业单位小时内广义费用的因素主要包括配送成本、环境成本与配送时间,即:
(1)配送时间
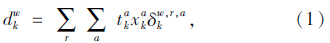
(2)环境成本
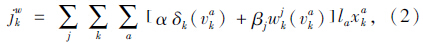
(3)配送成本

则广义费用的函数可以表示为:
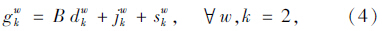
其中针对配送企业驾驶员的时间价值存在差异,按照式(1)的方法进行时间价值转换[12]:

综上所述,上层模型即配送企业的广义费用为:
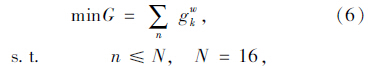
2.2 下层模型
考虑到驾驶员不可能完全掌握路网交通状态,其路径选择应该是个随机过程。因此,采用随机用户平衡配流模型刻画驾驶员的路径选择行为,即驾驶员以理解走行时间最小选择路径,并将交通分配的最终结果反馈给上层模型。下层模型的优化目标函数为各路径的行驶时间之和最小,具体模型为:
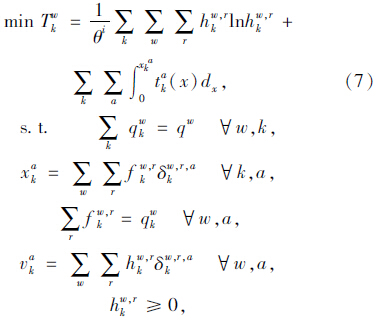
3 算法步骤 3.1 下层模型求解步骤
根据以上模型构建,就可以得出时限条件下,存在广义费用限制与时间限制的配送优化算法,算法的具体步骤如下。
Step 1:初始化。令qkw=,xkw=0,计算tka(0)。在OD对w之间的混合交通网络Gk中,寻找最短时间路径,计算OD对w之间的混合交通网Gk的各路径的行驶时间之和Tkw(0)。在OD对w之间混合交通网络Gk中,按照全有全无分配方法加载qiw(1),得到xka(1)。设置迭代次数n=1。
Step 2:根据kxa(n),计算tka(n)。
Step 3:在现有阻抗tka(n)上,执行一次运量随机加载,得到新的路段流量yka(n)。
Step 4:按照“相继平均”移动,迭代更新。计算:
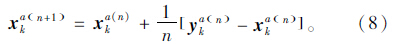
Step 5:收敛性检查。如果满足收敛条件,算法停止;否则,令n=n+1,转入step 2。
3.2 双层模型求解步骤
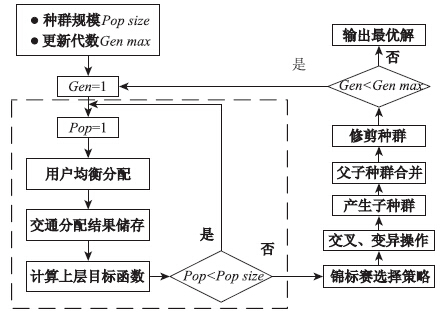
采用GA算法求解双层规划模型,根据用户均衡分配模型结果计算上层规划的目标函数,得到种群中每个个体的适应度,并进行选择、交叉、及变异等步骤,最终获得时限条件下城市物流配送问题的最优解集。算法流程如图3所示,具体操作步骤如下。
|
| 图3 GA算法流程图 Fig.3 Flowchart of genetic algorithm |
Step 1:初始化种群。
Step 1.1:设置GA算法参数,种群规模Pop size,种群进化代数Gen max;
Step 1.2:采用0-1编码方案,根据货车路径随机生成初始种群Population,设定种群代数计数器Gen=1。
Step 2:设定种群个体计数器pop=1,计算每个个体适应度。
Step 2.1:计算下层用户均衡模型,pop=pop+1;
Step 2.2:根据下层模型的分配结果计算上层模型的目标函数,并根据式(6)计算适应度函数,如果Pop<Pop size,转至step 2.1,否则转至step 3。
Step 3:GA核心操作。
Step 3.1:设定货车路径选择个体数目,确定货车路径种群;
Step 3.2:进行交叉、变异操作;
Step 3.3:产生子代种群,并对父、子种群进行合并,根据适应度函数排序,选取前Pop size个个体作为新一代种群。Gen=gen+1;
Step 3.4:如果Gen<Gen max,转至step 1.2;否则转至step 4。
Step 4:算法终止,产生最优解。
4 算例分析 4.1 基础数据
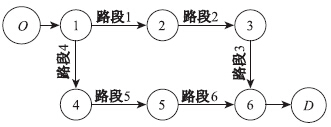
以图4所示的简单路网为例,对时限条件下的城市物流配送的优化与均衡分析模型的求解算法进行验证。
|
| 图4 算例配送网络 Fig.4 Distribution network of example |
混合交通Gk网络上路段的相关数据如表1所示。
| 路段 | ta(0)k/h | cak/(veh·h-1) | lak/km | |
| 路段1 | 小汽车 | 0.18 | 500 | 8 |
| 货车 | 0.11 | 700 | ||
| 路段2 | 小汽车 | 0.13 | 700 | 10 |
| 货车 | 0.10 | 800 | ||
| 路段3 | 小汽车 | 0.13 | 600 | 9 |
| 货车 | 0.09 | 700 | ||
| 路段4 | 小汽车 | 0.17 | 600 | 10 |
| 货车 | 0.12 | 600 | ||
| 路段5 | 小汽车 | 0.20 | 500 | 8 |
| 货车 | 0.15 | 700 | ||
| 路段6 | 小汽车 | 0.18 | 700 | 9 |
| 货车 | 0.13 | 900 | ||
本文算例假设在配送中心与配送目的地之间的路径中,路径1存在交通管制时间窗,该路径上的物流配送车辆仅在8∶00-11∶00之间不允许通行;且仅考虑一天中7:00-22:00间的城市物流配送的优化与均衡分析,要求配送货物无论是否受到交通管制时间窗限制,均需完成配送任务;同时,仅考虑车辆将货物配送至用户的配送过程,不考虑车辆完成配送任务后的回程。通过改变城市交通管制的管制区域与允许通行时间窗,本文设计了3种不同的交通情景,不同的交通情景具体介绍如下。
情景0:基础情景
在基础情景中,设定整个配送期t2为7:00-22:00,共有13 h,货物可直接由配送中心(O点)送到用户1(D点),OD点间不受任何交通管制政策的影响,货车可以自由进行配送。基础情景作为基准,通过与其进行对比,可以得出不同交通管制情景下城市配送优化的综合效益。
情景1:增加交通管制
在情景1中,设置交通管制时间段t1为8:00-11:00,通过在t1时间段内设置交通管制,物流配送仅能允许利用路径2到达用户1(D点),同时,剩余时间段被允许继续进行物流配送。
情景2:时限条件下将货物配送完毕
在情景2中,在时限条件下,通过OD对间2条路径进行物流配送,考虑在t1时间段内的3 h将货物全部配送完毕。
3种情景中混合交通网络Gk上的OD矩阵分布如表2所示。
| 情景 | 基础情景 | 时限情景1 | 时限情景2 | ||||||
| 时间段 | 无时间窗限制 8:00-11:00 |
6:00-22:00 | 总计 | 有时间窗限制 8:00-11:00 |
6:00-22:00 | 总计 | 有时间窗限制 8:00-11:00 |
6:00-22:00 | 总计 |
| 货车 | 小汽车 | 货车 | 小汽车 | 货车 | 小汽车 | ||||
| 6:00-7:00 | - | 800 | 800 | - | 800 | 800 | - | 800 | 800 |
| 7:00-8:00 | 100 | 1 200 | 1 300 | 100 | 1 200 | 1 300 | - | 1 200 | 1 200 |
| 8:00-9:00 | 100 | 1 000 | 1 100 | 100 | 1 000 | 1 100 | 400 | 1 000 | 1 400 |
| 9:00-10:00 | 100 | 2 000 | 2 100 | 100 | 2 000 | 2 100 | 500 | 2 000 | 2 500 |
| 10:00-11:00 | 100 | 2 000 | 2 100 | 100 | 2 000 | 2 100 | 400 | 2 000 | 2 400 |
| 11:00-12:00 | 100 | 3 000 | 3 100 | 100 | 3 000 | 3 100 | - | 3 000 | 3 000 |
| 12:00-13:00 | - | 2 000 | 2 000 | - | 2 000 | 2 000 | - | 2 000 | 2 000 |
| 13:00-14:00 | 100 | 1 000 | 1 100 | 100 | 1 000 | 1 100 | - | 1 000 | 1 000 |
| 14:00-15:00 | 100 | 3 000 | 3 100 | 100 | 3 000 | 3 100 | - | 3 000 | 3 000 |
| 15:00-16:00 | 100 | 2 000 | 2 100 | 100 | 2 000 | 2 100 | - | 2 000 | 2 000 |
| 16:00-17:00 | 100 | 1 000 | 1 100 | 100 | 1 000 | 1 100 | - | 1 000 | 1 000 |
| 17:00-18:00 | 100 | 4 000 | 4 100 | 100 | 4 000 | 4 100 | - | 4 000 | 4 000 |
| 18:00-19:00 | - | 2 000 | 2 000 | - | 2 000 | 2 000 | - | 2 000 | 2 000 |
| 19:00-20:00 | 100 | 3 000 | 3 100 | 100 | 3 000 | 3 100 | - | 3 000 | 3 000 |
| 20:00-21:00 | 100 | 1 000 | 1 100 | 100 | 1 000 | 1 100 | - | 1 000 | 1 000 |
| 21:00-22:00 | 100 | 1 000 | 1 100 | 100 | 1 000 | 1 100 | - | 1 000 | 1 000 |
取θ1=1,θ2=2。不同交通方式相关数据见表3。
| 交通方式 | 小汽车单位 折算系数Ek |
行驶中的单位时间 成本Ck/ (元·veh-1) |
p
ak/ [元· (veh·km)-1] |
93号油价α/ (元·L-1) |
能源消耗δk/ [L· (veh·km)-1] |
污染物排放的 环境成本βj/ (元·kg-1) |
污染物排放的 排放量wjk/ [g·(veh·km)-1 |
| 小汽车 | 1.0 | - | - | - | - | - | - |
| 货车(8t) | 2.0 | 2.3 | 3.6 | 7.597 | 6.4 |
COx=-0.3 NOx=-8.3 HC=-6.7 |
COx=-12.7 NOx=-7.2 HC=-1.9 |
配送企业的驾驶员在配送过程中的相关数据如表4。
| 指标 |
年平均工资/ (元·a-1) |
每年工作 时间/周 |
每周工作 时间/h |
时间价值/ (元·h-1) |
| 货车驾驶员 | 48 000 | 50 | 40 | 12 |
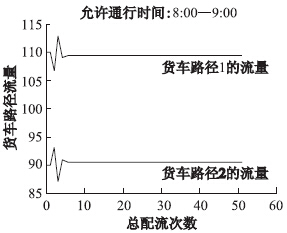
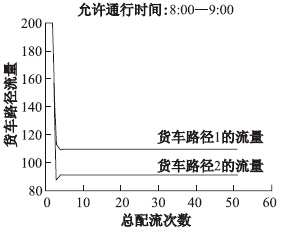
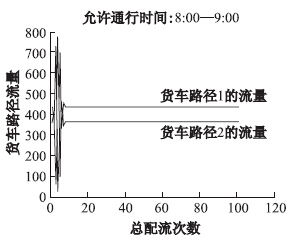
图5、图6、图7中显示的是求得最优解下的流量图,可以看出,算法具有明显的收敛性质。
|
| 图5 (基础情景)8:00-9:00货车最优解 Fig.5 Optimal solution of truck during 8:00-9:00 in basic situation |
|
| 图6 (时限情景1)8:00-9:00货车最优解 Fig.6 The optimal solution of truck during 8:00-9:00 in scene 1 |
|
| 图7 (时限情景2) 8:00-9:00货车最优解 Fig.7 Optimal solution of truck during 8:00-9:00 in scene 2 |
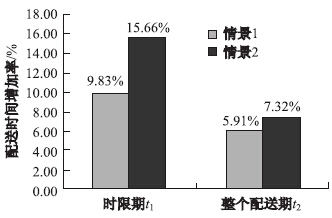
为了使城市交通管制情景下满足不同配送要求的物流配送优化结果的综合效益比较结果更加直观,通过情景1和情景2分别与基础情景进行比较,发现两种情景分别配送时间、环境成本和配送成本变化率上的差异,如图8、图9、图10所示。
|
| 图8 时限情景1、2下的配送时间增加比率 Fig.8 Increasing ratios of distribution time in scenes 1 and 2 |
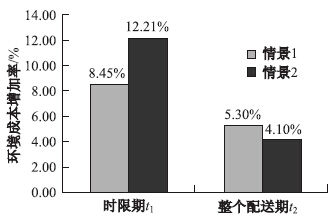
|
| 图9 时限情景1、2下的环境成本增加比率 Fig.9 Increasing ratios of environment costs in scenes 1 and 2 |
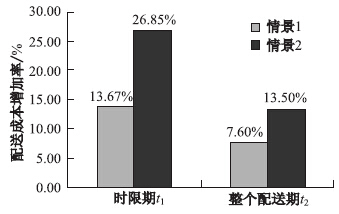
|
| 图10 时限情景1、2下的配送成本增加比率 Fig.10 Increasing ratios of distribution costs in scenes 1 and 2 |
图8显示了城市交通管制情境下满足不同配送要求的配送时间增加率。在时限情景1中的配送时间增加率低于时限情景2。
图9显示了城市交通管制情境下满足不同配送要求的环境成本增加率,在t2时间段内,时限情景1下的城市配送环境成本增加率高于时限情景2。
图10显示了不同城市交通管制情境下城市配送成本的增加率,情景2比情景1分别高出了13.18%和5.9%。
通过对算例结果进行分析,可以得到如下结果:
(1)在交通管制时限期间t1中,时限情景1设置交通管制,物流配送仅能允许利用路径2到达用户1(D点),同时,剩余时间段被允许继续进行货物配送;时限情景2需在该时间段内的3 h将货物全部配送完毕。两种情景下的配送时间、环境成本与配送成本均随之增加,其中,时限情景2的配送成本增加比例高达26.85%,主要是受到平均运费及交通需求的双重影响,在限时配送需求的约束下,增加配送车辆数量,导致网络交通需求量大幅提升,加剧城市路网拥挤程度,从而导致物流配送成本大幅增加。时限情景1在t1时间段的环境成本和配送时间增加比例分别为8.45%和9.83%,由于网络交通需求量变化较小,仅受到网络配送阻抗影响,能源消耗及污染物排放,其增加比例较小。
(2)对比t1时间段和t2时间段,交通管制时限期间的城市物流配送时间与配送成本的增加比例均高 于总体配送期间。而在t2时间段,时限情景1与时限情景2的交通总量是相同的,配送时间受到网络阻抗的影响,时限情景1比时限情景2的整体网络阻抗要小,为此时限情景1的增长比例为5.91%。时限情景2中,要求在交通管制的3个时间段内将货物全部配送完毕,与时限情景1相比,其配送时间集中于8:00-11:00。为此,虽然在时限期间物流企业的配送环境成本增长达到了12.21%,但是由于综合其他时间段的环境成本增加值较低,仅为4.1%。
总体而言,当在交通管制时限条件下按照用户要求进行配送时,物流配送企业的广义成本增大,而针对交通管制政策实施的物流配送服务,能够避开城市交通网络拥堵时段,使得物流配送企业的广义成本在一定程度上得到控制,同时降低物流配送车辆对城市交通的影响。
5 结论
本文给出了考虑交通系统不确定性的城市配送优化应用流程,并进行了综合运用与实际计算,对不同城市物流中的交通管制时间窗下的城市物流配送优化综合效益进行了对比分析。通过研究发现:当在城市物流配送过程中,增加交通管制的时间窗时,城市物流配送过程中的配送时间、环境成本与配送成本都有明显的增加,促使配送企业的广义费用增加,降低配送企业的效益;当在增加交通管制时间窗的基础上,要求在时间窗范围内将货物配送完毕时,会增加配送企业的配送时间及配送成本,降低了配送企业的环境成本。此外,本文假设了对城市物流配送的优化模型的输入参数,而如何合理确定城市物流配送优化模型的参数随机性以更好地描述实际问题还有待进一步深入研究。
| [1] | 邓爱民,王少梅,汪利君.城市物流配送系统优化研究[J].武汉理工大学学报:交通科学与工程版,2006,30(3):481-484.DENG Ai-min,WANG Shao-mei,WANG Li-jun. City Logistics Distribution System Optimization Research [J].Journal of Wuhan University of Technology: Transportation Science & Engineering Edition,2006,30(3):481-484. |
| [2] | 李作秋,王国林.一种有时间窗约束的非满载车辆调度问题中的启发式算法研究[J].公路交通科技,2006,23(7):147-149,153.LI Zuo-qiu,WANG Guo-lin. Study on a Heuristic Arithmetic for Vehicle Scheduling Problem of Non-full Loads with Time Windows[J].Journal of Highway and Transportation Research and Development,2006,23(7):147-149,153. |
| [3] | 戢晓峰,覃文文,焦新龙,等. 高强度快递需求区域移动仓库选址算法[J]. 交通运输工程学报,2012,12(6): 69-75.JI Xiao-feng,QIN Wen-wen,JIAO Xin-long,et al. Location Algorithm of Mobile Warehouse in Express Demand Region with High Strength[J].Journal of Traffic and Transportation Engineering,2012,12(6): 69-75. |
| [4] | 戢晓峰,陈方,覃文文,等. 时效约束的高强度快递需求区域车辆调度模型[J]. 武汉理工大学学报:交通科学与工程版,2013,37(2): 234-237.JI Xiao-feng,CHEN Fang,QIN Wen-wen,et al. HHigh Intensity Express Demand Region Vehicle Scheduling Model Under Time Restrains[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering Edition,2013,37(2): 234-237. |
| [5] | 戢晓峰,魏雪梅,董菁菁. 基于信息搜寻的物流信息组织模式研究[J]. 昆明理工大学学报:社会科学版,2013,13(1):56-63.JI Xiao-feng,WEI Xue-mei,DONG Jing-jing. A Research on Logistics Information Organization: A Mode Based on Information Search[J].Journal of Kunming University of Science and Technology: Social Science Edition,2013,13(1):56-63. |
| [6] | LUO Ya-ting,JI Xiao-feng,LIANG Fei-wen. Game Theory Analysis between Urban Logistics Distribution and Traffic Organization Scheme[C]//International Conference on Logistics Engineering and Management 2012. Virginia: The American Society of Civil Engineers,2012: 171-177. |
| [7] | 魏航.一种求解时变条件下有宵禁限制最短路的算法[J].管理科学学报,2009,12(1):9-17.WEI Hang. An Approach for Time-varying Shortest Path Problem with Curfews[J].Journal of Management Sciences in China,2009,12(1):9-17. |
| [8] | 卢冰原,吴义生,程八一.具有模糊时间约束的城市配送多车型车辆调度问题[J].公路交通科技,2011,28(11):152-158.LU Bing-yuan,WU Yi-sheng,CHENG Ba-yi. Multi-type Vehicle Scheduling Problem in City Distribution with Fuzzy Time Restraints[J]. Journal of Highway and Transportation Research and Development,2011,28(11):152-158. |
| [9] | 焦朋朋,陆化普,王建伟.基于交通效率的城市道路网络优化[J].清华大学学报:自然科学版,2005,45(3):297-300.JIAO Peng-peng,LU Hua-pu,WANG Jian-wei. Optimization of Urban Road Network Based on Transport Efficiency[J].Journal of Tshinghua University: Science and Technology Edition,2005,45(3):297-300. |
| [10] | 胡云超,申金升,黄爱玲.城市货运交通管制情景下城市配送多目标优化效益研究[J]. 交通运输系统工程与信息,2012,12(6):119-125,144.HU Yun-chao,SHEN Jin-sheng,HUANG Ai-ling. Multi-objective Optimization for City Distribution under Urban Freight Restriction[J].Journal of Transportation Systems Engineering and Information Technology,2012,12(6):119-125,144. |
| [11] | 陈荔,马荣国.基于生态交通效率的城市道路网络优化模型[J].中国公路学报,2009,22(5):100-104.CHEN Li,MA Guo-rong. Urban Road Network Optimization Model Based on Eco-transport Efficiency[J].China Journal of Highway and Transport,2009,22(5):100-104. |
| [12] | 刘强,陆化普,王庆云.区域运输通道布局优化三层规划模型[J].清华大学学报:自然科学版,2010,50(6):815-819.LIU Qiang,LU Hua-pu,WANG Qing-yun. Tri-level Programming Model for Optimization of Regional Transportation Corridor Layout[J]. Journal of Tshinghua University: Science and Technology Edition,2010,50(6):815-819. |
 2014, Vol. 31
2014, Vol. 31
