扩展功能
文章信息
- 孙文圃, 许金良, 刘文君
- SUN Wen-pu, XU Jin-liang, LIU Wen-jun
- 交通环境对高速公路运营安全性影响综合评价
- Comprehensive Evaluation of Effect of Traffic Environment on Expressway Traffic Operational Safety
- 公路交通科技, 2014, Vol. 31 (12): 124-131,138
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 124-131,138
- 10.3969/j.issn.1002-0268.2014.12.020
-
文章历史
- 收稿日期:2014-10-20
2. 东营市公路勘察设计院, 山东 东营 257091
2. Dongying Highway Surveying & Designing Institute, Dongying Shandong 257091, China
高速公路以其快速、便捷的特点对道路运输起着至关重要的作用,然而由于高速公路车速高、超载严重以及人为因素等原因,其事故伤害程度更为严重,事故损失更为惨重,因此研究交通环境中道路条件、交通条件、互通式立体交叉等因素对高速公路安全性的影响,是降低高速公路高事故率导致的负面社会影响、减少运营管理部门损失的必要举措。
国外从20世纪50年代开始对事故与道路安全影响因素的关系进行研究,起初采用描述统计学的方法,用图表描绘事故与影响因素的关系图,用以甄别事故黑点。但这种方法获得的事故模型有局限性,其反映的是单变量的、局部的影响因素,难以体现出道路、交通条件对交通安全的综合作用[1, 2, 3]。90年代以后,国外众多学者根据多元统计回归分析的方法,建立多影响因素的事故预测模型,且广泛运用于工程实例中,主要有泊松回归分析模型、负二项回归模型、美国联邦公路局模型等。这些模型在工程实例中,或多或少存有模型参数不合理、模型质量评定方法不科学、交通条件对事故的综合影响难以表达等问题。
国内对道路事故预测多是宏观层面,先后提出了灰色模型、神经网络、马尔可夫模型等预测方法。微观层面的事故预测研究,多是利用描述统计学的理论,采用图表观测事故随道路交通条件变化的一般规律,以甄别事故黑点。长安大学周晓光提出了与纵坡、曲线半径有关的长大下坡事故预测模型[4];韩跃杰在分析了国内外研究现状基础上,提出了道路横断面因素的事故预测模型[5];苏英平采用山东和青海两省的多条公路不同路段的线形参数和运行车速的观测资料,建立了适应于我国的纵坡运行车速预测模型[6]等。现已建立的道路事故预测模型中大多以单方面因素的事故数为评价依据,缺乏交通环境中多因素对公路交通安全综合影响的评价。因此,结合我国道路交通实际研究现状,建立事故预测模型,进行安全评价,以便主动采取相应的改善措施,对保障我国道路交通安全,降低事故率,具有实践意义。 1 高速公路运营安全性评价模型的建立 1.1 道路条件对高速公路安全性影响的评价模型 1.1.1 模型变量的确定:
本文中的预测模型以互通式立体交叉为节点,两座相邻互通式立交之间的间距为预测路段长度,每一路段包含多个平曲线、竖曲线及纵坡要素。道路的平面线形、纵断面、横断面都是组成道路特性的重要因素,它们的共同作用影响了车辆的行驶安全。因此,应将上述各因素作为一个整体进行考虑,综合考虑各因素对安全的影响。
(1)平曲线因素
预测模型中平曲线因素用路段内第i条平曲线的权值WHi和其对应的平曲线曲度DEGi联合表征,即:

(2)竖曲线因素
竖曲线因素用路段内第j条竖曲线的权值WVj和与其相对应的竖曲线曲率Vj联合表征,即:

(3)纵坡因素
纵坡因素用路段内第k个坡度段的权值WGk和与其对应的绝对坡度值GRk联合表征,即:\

(4)横断面因素
其中车道数将在交通量与事故率的关系预测模型中体现,而高速公路车道宽度基本都按规范规定取3.75 m,所以在道路条件与事故率的关系预测模型中不予以考虑,只考虑中间带宽度MW、路肩宽度SW及路侧危险度RHR。
本文根据我国实际情况,在综合考虑边坡、路侧安全净区、交通安全设施基础上,对路侧危险度进行划分如表 1所示。
| 路侧安全等级 | 描述 |
| I级 | 路侧净区宽度充足,通常达到4 m以上,且基本无障碍物;边坡平坦,坡度小于1∶3,以保障车辆误驶离公路后可以自行驶回;车辆一般不会发生碰撞或翻车事故,可不设置护栏;路段视线诱导设施可视性、连续性好,设置密度合理;标志牌可视性好,设置距离、位置合理,标线清晰。 |
| II级 | 路侧净区宽度小,一般不超过3 m,路侧区域可能存有少量、零散树木、标志杆柱等障碍物,行车道边缘较近区域可能有边沟、挡墙等危险物;边坡坡度大于1∶3,车辆驶离公路后无法自行返回,但冲出路外的车辆通常能得到有效控制;路段视线诱导设施可视性、连续性良好,设置密度较合理,标志牌可视性良好,设置距离、位置较合理,标线清晰。 |
| III级 | 路侧净区宽度不足,一般不大于1.5 m;路侧边坡较陡,深度不低于3 m;行车道边缘外存在宽大边沟、崖壁等危险物,车辆误入边沟,发生翻车事故的概率较大;路段视线诱导设施可视性、连续性、设置密度能满足需求;标志牌可视性良好,设置距离、位置满足行车需求,标线较清晰。 |
| IV级 | 路侧净空宽度严重不足,通常在1 m以下;路侧地形一般为陡崖、深沟或高度在4 m以上的高填方边坡、挡墙等;行车道外侧边缘一定区域内多存在河流、湖泊等,车辆驶出公路,容易发生重大、特大交通事故;路段视线诱导设施可视性、连续性、设置密度达不到规范规定;标志牌可视性、设置距离、位置满足不了行车安全需求,标线有损,不清晰。 |
国际上研究较多的事故预测模型是泊松分布模型,在单位时间内观测到发生ni次事故的概率P(ni) 用泊松分布模型表示如下:
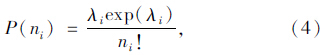
期望事故次数可被定义为事故影响因素的函数即
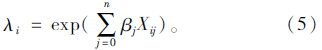
因此,考虑平纵横因素的事故率预测模型如下
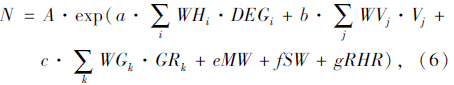
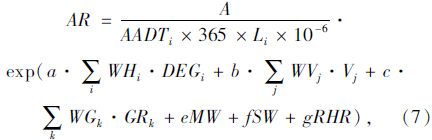
对西潼、西阎、西安咸阳机场高速收集的线形资料及事故资料进行分析,得到17组数据,对17组数据进行回归分析得到的拟合参数见表 2。
| 模型 | 非标准化系数 | 标准 系数 试用版 |
t | Sig. | B的95.0% 置信区间 |
||
| B | 标准 误差 |
下限 | 上限 | ||||
| (常量) | 2.438 | 2.341 | 1.042 | 0.322 | -2.777 | 7.653 | |
| 平面要素 | -0.518 | 0.268 | -0.521 | -1.935 | 0.082 | -1.116 | 0.079 |
| 竖曲线 | -3.332 | 2.010 | -0.570 | -1.657 | 0.128 | -7.811 | 1.147 |
| 坡度 | 1.086 | 0.568 | 0.469 | 1.912 | 0.085 | -0.179 | 2.351 |
| MW | -0.380 | 0.295 | -0.288 | -1.287 | 0.227 | -1.038 | 0.278 |
| SW | 0.533 | 0.400 | 0.295 | 1.332 | 0.212 | -0.358 | 1.424 |
| RHR | 0.461 | 0.214 | 0.429 | 2.157 | 0.056 | -0.015 | 0.937 |
| 注: 因变量为ln N | |||||||
对回归方程需要进行统计检验。相关系数为0.854,说明变量ln N与其他变量之间具有高度显著的线性关系。统计量F=4.473,F>F0.025(6,17-6-1),因此,在0.975的置信概率下,模型的关系显著成立。t>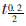 17-1,则在0.8的置信概率下变量对事故的影响是显著的。模型中所有系数都有统计学意义。由残差分析得残差分布是正态的,样本是来自正态的总体,满足回归分析的正态性假设。
17-1,则在0.8的置信概率下变量对事故的影响是显著的。模型中所有系数都有统计学意义。由残差分析得残差分布是正态的,样本是来自正态的总体,满足回归分析的正态性假设。
综上所述,得到道路条件对高速公路安全性的事故预测模型为:

模型通过评价和各项检验,具有良好回归效果。 1.2 交通条件对高速公路安全性影响的评价模型 1.2.1 模型变量的确定
V/C是指路段交通量与相应通行能力之比,V/C比交通量能更好地反映出道路交通状况,反映出道路拥挤程度,与事故的关系也较为密切[7]。V/C综合考虑了车道数、车辆组成修正系数、车道宽度修正系数、路肩宽度修正系数。当研究道路包含多个路段,且道路条件及交通组成变化较大,比较复杂时,采用V/C建立事故预测模型说服力更强。 1.2.2 模型形式的选择
本文选用高速公路单向N条车道的路段实际通行能力进行计算,如下式所示:
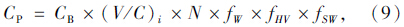
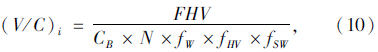
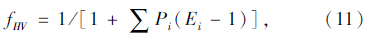
| 车型编号 | 代表车型 | 折算系数 | 车型说明 |
| 1 | 小客车 | 1.0 | ≤19座的客车和载重量≤2 t的货车 |
| 2 | 中型车 | 1.5 | >19座的客车和2 t<载重量≤7 t的货车 |
| 3 | 大型车 | 2.0 | 7 t<载重量≤14 t的货车 |
| 4 | 拖挂车 | 3.0 | 载重量>14 t的货车 |
通过分析大量数据,拟合(V/C)i与事故的关系,得出相应的事故预测模型。 1.2.3 事故预测模型的建立
对3条高速交通量、交通组成与事故率数据整理,将数据做成散点图,通过SPSS统计软件,进行曲线拟合,模型汇总及参数表如表 4所示。
| 方程 | 模型汇总 | 参数估计值 | ||||||
| R2 | F | df1 | df2 | Sig. | 常数 | b1 | b2 | |
| 线性 | 0.433 | 23.693 | 1 | 31 | 0.000 | 0.545 | -0.567 | |
| 对数 | 0.456 | 26.004 | 1 | 31 | 0.000 | 0.032 | -0.334 | |
| 二次 | 0.508 | 15.486 | 2 | 30 | 0.000 | 1.442 | -3.695 | 2.685 |
| 指数 | 0.402 | 20.871 | 1 | 31 | 0.000 | 0.906 | -2.537 | |
| 注:自变量为 V/C。 | ||||||||
由表 4可看出,二次方程拟合程度最高,因此,选用二次方程作为事故预测模型。百万车事故率与V/C的关系为
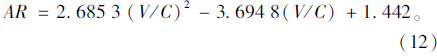
相关系数R2为0.508,说明事故率与V/C之间相关性强。统计量F=15.486,F0.005(1,33-1-1)=9.18,F>F0.05,因此,在0.995的置信概率下,模型的关系显著成立。
1.3 互通式立体交叉对高速公路安全性影响的评价模型 1.3.1 立交间距对高速公路安全性影响的事故预测模型
国外关于立交间距对道路安全性的影响研究较为透彻,美国联邦公路局(FHWA)通过对加利福尼亚州95个不同立交间距5 a的事故数据进行分析,得到以下事故预测模型[9]:
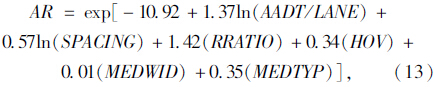
该模型通过华盛顿州的数据检验,表明具有良好的适应性。本文结合我国道路实际情况,对此模型进行修正。通过前文3条高速相关资料及事故资料,采用SPSS软件统计回归,得到立交间距对高速公路安全性影响评价模型为:
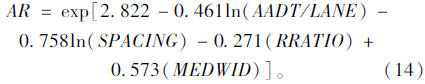
用前文方法对模型进行检验,得到模型关系显著成立,通过检验。 1.3.2 立交匝道对高速公路安全性影响的事故预测模型
研究表明,立交匝道安全性的首要影响因素是主线和匝道的两个交通流变量,其次是匝道位置、匝道类型、高速公路和匝道设计速度之间的差异和变速车道长度。本论文参照Hauer的方法进行立交匝道事故预测模型的建立,即每个变量依次进入模型,判断其在模型中的贡献率。具体操作过程为将事先选择的变量逐一地引入方程中,对于可量化变量,绘制引入变量的方程的经验积分函数(EIF)图,与常规函数的累计函数进行对照,若积分函数曲线基本呈直线,与各种函数都不相符,则表明变量不显著,剔除该变量;对于不可量化变量,判断其相关性R2,确定是否保留在方程中,直到检验了每个变量的显著性为止,确保方程中仅保留显著性高的变量[10]。
(1)主线AADT
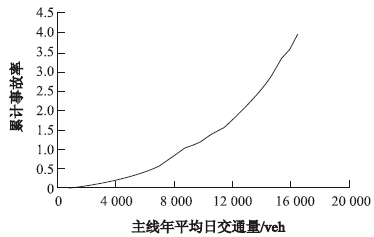
图 1显示了主线AADT变量的EIF,对EIF与已知的函数进行比较来检测事故和主线AADT之间的适应关系。
|
| 图 1 主线AADT对应事故率的经验积分函数图 Fig. 1 EIF of main AADT for accident rate |
与常用的f(x)(密度函数)和F(x)(累积函数)的一般函数形式对照,认为伽玛函数和幂函数比较相符。为确定哪个函数更适合用来描述事故率和主线AADT之间的关系,表 5给出了估计的伽玛函数拟合度和幂函数拟合度。
| 函数 | 模型 | 拟合优度 |
|
伽玛 函数 |
y=0.637×(MainAADT/10000)0.517· exp[0.09×(MainAADT/10000)] |
2log Λ=1 874.1 AIC=1 882.1 |
| 幂函数 | y=0.438×(MainAADT/10 000)1.069 |
2log Λ=1 880.3 AIC=1 886.3 |
表中似然比检验定义为:
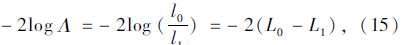
除了似然比检验,还采用赤池信息准则AIC(Akaikes information criterion)来表征拟合优度。AIC的定义是:
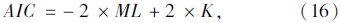
AIC由两部分组成,第一部分显示了回归模型的拟合精度,值越小越好;第二部分显示了回归方程建立过程中变量数的多少,即模型的复杂程度,值也是越小越好,这一部分实际上也是对自变量个数或模型中参数个数的“惩罚”。因而,AIC越小越好[11]。表 5可得,伽玛函数的拟合优度比幂函数更好。
(2)匝道AADT
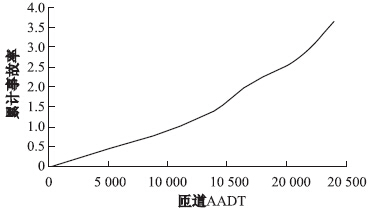
图 2示出了匝道AADT变量的EIF,用所观察到的事故与在上一步中建立的模型预测的事故的比率。图 2显示,匝道交通量高达10 000 veh/d之前,事故不依赖于匝道交通量,因为EIF是一条直线。但是,交通量达到10 000 veh/d之后,EIF是指数函数或幂函数的形式。
|
| 图 2 匝道AADT对应事故率的经验积分函数图 Fig. 2 EIF of ramp AADT for accident rate |
表 6显示了估计的指数函数和幂函数的匝道交通量超过10000 veh/d时的拟合优度。指数函数的拟合优度似乎比幂函数更好。
| 函数 | 模型 | 拟合优度 |
| 指数函数 |
y=0.706×{(MainAADT/10000)0.488 exp[0.069(MainAADT/10000)]}× exp[0.479(RampAADT/10000)] |
2LogΛ=1838.8 AIC=1848. |
| 幂函数 |
y=0.711×{[(MainAADT/10000)0.438 exp[0.082(MainAADT/10000)]}× (RampAADT/10000)1.591 |
2LogΛ=1842.9 AIC=1852.9 |
(3)匝道位置和类型
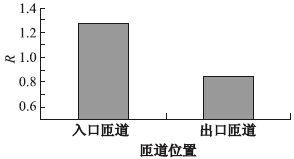
匝道位置分为出口匝道和入口匝道,匝道类型分为左转匝道和右转匝道。首先,通过已有模型估计匝道位置与事故关系的R比率,见图 3。因为出口、入口匝道的事故显著不同,因此匝道位置变量应该被引入到事故预测模型中。因为匝道位置是二进制因子,对于出、入口匝道,选用一阶线性形式是比较合适的。模型中添加了匝道位置变量的线性函数后,模型的参数被重新估计。
|
| 图 3 SCB试验原理图 Fig. 3 Principle diagram of SCB test |
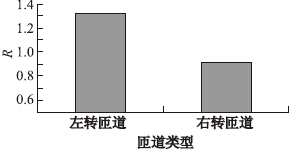
接着,匝道类型,图 4显示了事故和匝道类型之间的R比率关系。可以看出,R比率与左、右转匝道之间的关系是显而易见的,因此,匝道类型也用一阶的线性形式添加到模型中,因为匝道类型也是一个二进制因子。
|
| 图 4 匝道类型相关的事故的R比率 Fig. 4 R-ratios of accidents related to ramp types |
(4)高速公路主线和匝道设计速度之间的差异(Diff)
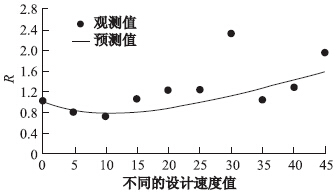
估计了高速公路主线和匝道的设计速度之间差与事故的R比率,先前已定义的函数形式有主线AADT、匝道AADT、匝道位置和类型。设计速度差与R-比率之间的关系见图 5。
|
| 图 5 设计速度差相关的事故的R比率 Fig. 5 R-ratios of accidents related to designed speeds |
R-比率图似乎是一个非对称关系。也就是说,在设计速度差10 kg/h,事故似乎减少,然后不断增加。关系是由式(17)的函数形式表示:
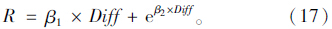
(5)变速车道长度
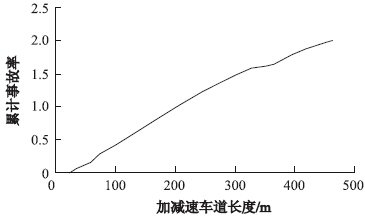
使用前面步骤创建的模型估计变速车道长度变量的EIF。因为EIF和变速车道长度之间的关系变量基本呈直线关系,见图 6,这与常用的累计函数曲线均不相符,即该变量与事故之间不存在一个显著的关系。因此,变速车道长度在最终的模型中被排除。
|
| 图 6 变速车道长度对应事故率的经验积分函数图 Fig. 6 EIF of accident rate corresponding to speed-change lane length |
因此,最终得到的预测模型如下式:

如果是右转匝道,则b2=1;如果是左转匝道,b2=1.712;
如果是出口匝道,则b3=1;如果是入口匝道,b3=1.359。
此外,豪尔模型估算出左转匝道是右转匝道的碰撞事故的2.71倍,入口匝道是出口匝道事故的2.36倍。
对模型进行验证,参数和似然比统计如表 7所示。
| 步骤 | 估计参数 | 统计量 | |||||||||
| K | Con | 主线AADT | 匝道AADT | 匝道位置 | 匝道类型 | 速度差 | df | Log | AIC | P-value | |
| 1 | 0.735 | 2.766 | 72 | -1 028.4 | 2 060.8 | <0.001 0 | |||||
| 2 | 0.329 | 0.639 |
0.515 0.090 | 70 | -937.1 | 1 882.2 | <0.001 0 | ||||
| 3 | 0.252 | 0.706 |
0.488 0.065 | 0.475 | 69 | -919.4 | 1 848.4 | <0.001 0 | |||
| 4 | 0.209 | 0.694 |
0.282 0.110 | 0.350 | 0.567 | 68 | -907.6 | 1 827.2 | <0.001 0 | ||
| 5 | 0.175 | 0.591 |
0.311 0.101 | 0.367 | 0.558 | 0.356 | 67 | -899.0 | 1 811.9 | <0.001 0 | |
| 6 | 0.153 | 0.575 |
0.339 0.097 | 0.342 | 1.712 | 1.359 |
-0.082 0.035 | 65 | -892.1 | 1 802.1 | 0.001 0 |
表 7显示了豪尔方法在模型建立过程中的参数和似然比统计。正如预期的那样,主线AADT是主导因素,其次是匝道AADT,匝道位置,类型和速度差变量。 2 交通环境对高速公路运营安全性的综合影响评价
评价一条高速公路交通安全水平涉及到道路线形、安全设施、交通量、交通组成、立交间距等很多方面的因素,片面地选取一个或几个指标进行评价达不到交通安全评价的目的,因此,需要建立一套完整的评价体系对道路安全进行综合分析和评价。 2.1 综合评价体系
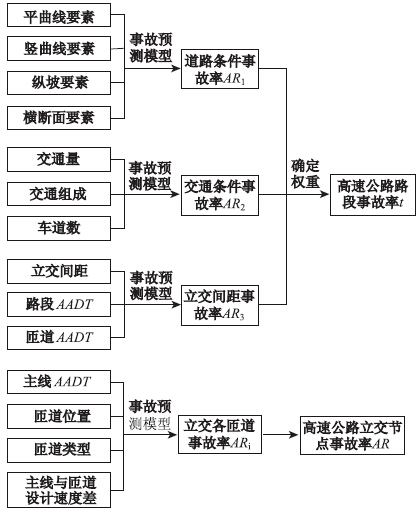
高速公路综合安全评价体系是一个多因素、多层次的复杂系统,本文交通环境对高速公路运营安全影响的综合评价体系结构如图 7所示。
|
| 图 7 高速公路运营安全性综合评价体系图 Fig. 7 Expressway operation safety comprehensive evaluation system |
(1)高速公路路段综合评价模型
本文采用层次分析法确定道路条件、交通条件和立交间距对高速公路安全性影响的权重,进而建立综合评价模型。
① 构造判断矩阵
AHP法在对指标的相对重要性进行评价时,引入了九分位的比例标度,见表 8。判断矩阵M中元素bij为i行指标相对j列指标进行重要性比较后的值[12]。
| 甲指标比 乙指标 |
极 重要 |
很 重要 | 重要 |
略 重要 | 同等 |
略 次要 | 次要 |
很 次要 |
极 次要 |
| 甲指标评价值 | 9 | 7 | 5 | 3 | 1 | 1/3 | 1/5 | 1/7 | 1/9 |
| 注:取8,6,4,2,1/2,1/4,1/6,1/8为上述评价值中间值 | |||||||||
构建高速公路安全性评价因子判断矩阵M,道路条件、交通条件、立交间距分别为B1,B2,B3。则判断矩阵M为:
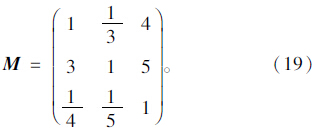
② 权重向量的计算
用几何平均法计算权重向量ω。
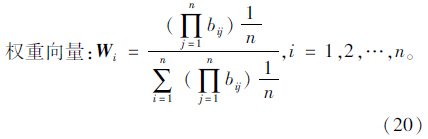
计算步骤:M的元素按行相乘得一新向量;将新向量的每个分量开n次方;将所得向量归一化即为权重向量。
权重向量计算表见表 9。
| 判断矩阵 | 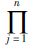 bij bij |
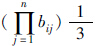 |
权重ω | |||
| B1 | B2 | B3 | ||||
| B1 | 1 | 1/3 | 4 | 1.333 333 3 | 1.100 642 | 0.279 688 |
| B2 | 3 | 1 | 5 | 15 | 2.466 212 | 0.626 696 |
| B3 | 1/4 | 1/5 | 1 | 0.050 000 0 | 0.368 403 | 0.093 616 |
计算特征根λmax=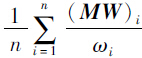 =3.085 766 7。
=3.085 766 7。
③ 一致性检验
根据特征值计算CI=λmax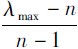 =0.042 883 35,三阶判断矩阵的RI值为0.58,因此计算CR=CI/RI=0.07393<0.1,表明该判断矩阵具有令人满意的一致性。
=0.042 883 35,三阶判断矩阵的RI值为0.58,因此计算CR=CI/RI=0.07393<0.1,表明该判断矩阵具有令人满意的一致性。
因此,根据计算的权重值,得到高速公路路段综合评价模型为:
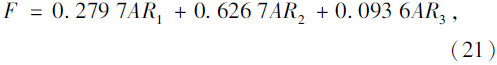
(2)节点立交综合评价模型
对于互通式立交节点处的事故率,采用各个匝道上事故率的均值来评价节点立交的安全性,即:

根据收集的设计资料、道路行车条件与交通量相似的多条具有代表性的高速公路的交通事故数据,采用数理统计法建立了高速公路基于事故预测的评价标准。通常认为某一路段发生的事故次数近似服从正态分布,定义随机变量:

随机变量Z服从正态分布,取置信度为98%,则当Z>2.33时,路段安全水平为差;当Z<-2.33时,路段安全水平为好;当-2.33≤Z≤2.33时,路段安全水平为中等。按照上述思路,针对高速公路路段及立交节点提出了事故预测模型的评价标准,如表 10、表 11所示。
| 安全水平 |
事故率AR评价标准/ [次·(×106 veh·km)-1] | 评价标准描述 |
| 好 | AR<0.61 | 较安全 |
| 中 | 0.61≤AR≤1.16 | 可接受 |
| 差 | AR>1.16 | 较差 |
| 安全水平 |
事故率AR评价标准/ [次·(×106 veh·km)-1] | 评价标准描述 |
| 好 | AR<0.86 | 较安全 |
| 中 | 0.86≤AR≤2.91 | 可接受 |
| 差 | AR>2.91 | 较差 |
(1)采用系统工程,统计回归的方法,建立了路段的道路条件事故预测模型、交通条件事故预测、立交间距事故预测模型、立交匝道事故预测模型,并对模型进行了验证,具有良好的适用性。
(2)建立了交通环境对高速公路运营安全性影响综合评价体系,结合层次分析法提出高速公路路段及立交节点的综合评价方法及评价标准。
(3)论文采用的事故预测模型是从国内外研究成果中经过分析修正得到的,利用事故预测模型计算得到的结果与实际情况可能存在一定差异,需进一步收集大量实际数据,进而对模型中的参数进行优化。
(4)影响高速公路安全性的因素众多,本文只研究了道路条件、交通条件、互通式立体交叉口对高速公路运营安全性的影响,需进一步分析气象资料、路面资料,研究天气、路面条件对公路安全性的影响,对已有模型进行补充。
| [1] | DEACON J A,ZEGEER C V,DEEN R C. Identification of Hazardous Rural Highway Locations[J].Transportation Research Record,1975,543:6-33. |
| [2] | TANNER J. Accidents at Rural 3-way Junctions[J]. Journal of the Institute of Highway Engineers,1953,2(11): 56-67. |
| [3] | HAKKERT A S,MAHALEL D. Estimating the Number of Accidents at Intersections from the Knowledge of Traffic Flows from the Approaches[J]. Accident Analysis and Prevention,1978,10(1): 69-79. |
| [4] | 周晓光. 青海省长大下坡交通事故预测模型的建立[D]. 西安: 长安大学,2007.ZHOU Xiao-guang. Establishment of Forecast Model of Traffic Accidents on Long and Steep Downgrades in Qinghai Province[D]. Xi'an: Chang'an University,2007. |
| [5] | 韩跃杰. 道路横断面因素对自由流车辆行驶速度及交通安全影响研究[D]. 西安: 长安大学,2006.HAN Yue-jie. Effect of Highway Transect Factors on Free Flow Vehicle Speed and Traffic Safety [D]. Xi'an: Chang'an University,2006. |
| [6] | 苏英平. 双车道二、三级公路纵断面线形与交通安全的关系[D]. 西安: 长安大学,2006.SU Ying-ping. Relationship of Two-lane Second Grade and Third Grade Highway Profile Alignment with Traffic Safety[D]. Xi'an: Chang'an University,2006. |
| [7] | 吉小进,方守恩. 高速公路基本路段V/C比与事故率的关系[J]. 公路交通科技,2003,20(1):122-123. JI Xiao-jin,FANG Shou-en. Relationship Between V/C and Accident Rates at Basic Expressway Section[J]. Journal of Highway and Transportation Research and Development,2003,20(1):122-123. |
| [8] | 王海燕. 高速公路交通安全评价体系研究[D]. 西安: 长安大学,2009.WANG Hai-yan. Study on Expressway Traffic Safety Evaluation System [D]. Xi'an: Chang'an University,2009. |
| [9] | PETER P,JOE G. Safety Assessment of Interchange Spacing on Urban Freeways[R]. McLean: Highway Research Center of Turner-Fairbank,2007. |
| [10] | JAE P M. Comparing Operation and Safety between a New Nano Interchange and Conventional System Interchange [D]. Raleigh: North Carolina University,2007. |
| [11] | 孙瑜. 道路安全设计模型(IHSDM)的应用研究[D]. 南京: 东南大学,2009.SUN Yu. Application of Highway Safety Design Model(IHSDM) [D]. Nanjing: Southeast University,2009. |
| [12] | 汪应洛. 系统工程[M]. 北京: 机械工业出版社,2003. WANG Ying-luo. Systems Engineering [M]. Beijing: China Machine Press,2003. |
 2014, Vol. 31
2014, Vol. 31
