扩展功能
文章信息
- 李长城, 文涛, 刘小明, 荣建
- LI Chang-cheng, WEN Tao, LIU Xiao-ming, RONG Jian
- 基于高速公路收费数据的行程时间可靠性模型研究
- Study on Reliability Model of Travel Time Based on Expressway Toll Data
- 公路交通科技, 2014, Vol. 31 (12): 110-115
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 110-115
- 10.3969/j.issn.1002-0268.2014.12.018
-
文章历史
- 收稿日期:2014-02-21
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
随着我国公路交通网络日益完善,公众出行活动日益频繁,社会公众对出行信息服务的需求更强,要求也越来越高,传统的静态路径导航、反映交通拥堵的红黄绿运行状态显示、路况事件信息发布等已难以满足公众对动态、深层次出行信息的需求。行程时间信息可以为出行者出行前的出行计划决策和途中的提示与诱导提供重要参考,为出行者提供更及时、准确、可靠的行程时间服务,是智能交通系统提供的重要服务内容之一,也是提高公众出行满意度的主要途径。
目前,国内各级高速公路联网收费中心都存有海量的历史收费数据,收费数据中蕴含着大量有价值的信息,通过对这些数据的挖掘,除可以为区域路网OD出行分布、交通需求时空变化、路网拥堵分析与改扩建扩容等提供决策外,还可以挖掘路网运行态势、行程时间预测等信息,为公众提供更多潜在价值信息。然而,目前按国内对海量收费数据的挖掘利用重视程度不够,针对海量收费数据的知识挖掘技术研究也相对较少。本文正是在此背景下,从行程时间预测角度,研究利用高速公路收费数据建立行程时间可靠性模型,以期为出行者提供行程时间参考信息。需要补充的是,收费数据与其他交调或车检器数据相比具有数据质量高、实效性强、格式统一等诸多优点,且能够反映车辆路径即含有OD信息,此外,现阶段我国高速公路上车检器布局总体而言还相对稀疏,仅靠交调或车检器数据还难以满足路网运行状态研判和出行信息服务的需求,因此,在利用收费数据挖掘交通运行信息方面,与交调或车检器数据是互为补充的。 1 文献综述
行程时间可靠性描述了交通出行能够在某一时间范围内完成的概率,反映了行程时间的稳定性、波动性以及出行者在预期行程时间内完成出行的可能性,是交通管理者和出行者都最为关心的指标之一。国内外的许多专家学者开展了行程时间可靠性的研究工作。
Asakura于1991年提出了行程时间可靠度的概念,定义行程时间可靠度的概念为:对于给定的一个OD对,出行者能在规定时间内顺利完成出行的概率[1]。Bell等人于1999年提出一种基于Logit的Sue分配方法的路径流量估计模型(The path flow estimator,PFE)。通过PFE可得到路径流量、路段流量、出行时间和路网的OD矩阵,并以此为依据估计道路交通系统的运行时间可靠度[2]。Inouye根据SUE均衡分配模型的特点,提出利用该模型分配得到的路径行程时间均值和方差、路段流量等计算行程时间可靠度[3],将行程时间的不同变化范围进行划分,对交通流状态服务水平进行了分级讨论。William等人提出了交通流模拟器模型TFS(Traffic Flow Simulator)[4]计算运行时间可靠度,该模型假定路段和路径的运行时间服从正态分布,路段出行时间的均值和方差可通过多次模拟得到。Wakabayashi对非常态下路网行程时间可靠度进行了相关研究[5],建立了在不确定的雨雪天气下的行程时间可靠度计算方法的框架,得到不同天气状况和交通控制策略下路网的行程时间可靠度。Arezoumandi[6]通过分析伽马分布、最大极值分布、Log-logistic概率分布、对数正态分布及威布尔分别与24 h行程时间数据的拟合程度,得到了可变限速情形下行程时间的分布服从对数正态分布。
裴玉龙等用行程时间可靠性对公路网运营可靠度进行了分析,并利用蒙特卡洛模拟法(Monte Carlo)进行了模拟计算[7]。刘海旭等通过分析随机路网中行程时间的随机变动,将OD交通量和路段通行能力作为离散随机变量,基于用户平衡分配模型,用近似算法求解行程时间可靠度[8]。李先等2007年以北京市出租汽车IC卡采集到的行程时间数据为基础,研究提出了新的单位距离行程时间可靠性评价指标和方法[9]。2004年熊志华针对路段之间的相互影响模式分析了路网行程时间可靠性[10]。熊志华、邵春福等认为道路网在正常状态与失效状态之间存在过渡过程,提出模糊行程时间可靠性的概念,并将其理论应用扩大到能同时处理随机和模糊这两种现象[11]。陈小鸿等针对正态分布或对数分布不能有效地描述小间隔行程时间分布的问题,提出基于浮动车数据的行程时间经验分布[12]。陈琨等[13]通过曲线拟合建立了路段行程时间的正态分布模型,并利用统计学理论,分别考虑路段相关和路段独立两种情况,建立了基于对数正态和分布的路径行程时间可靠性评价模型。朱彦等[14]以城市快速路为研究对象,使用浮动车数据计算出路段在不同时段的行程时间,再采用统计分析方法得出目标路段在相同时段下行程时间的分布规律,并对相同时段不同路段、相同路段不同时段的行程时间分布测度进行对比分析。
从国内外已有研究来看,研究人员从不同角度、针对不同研究对象、利用不同研究数据对行程时间可靠性进行了大量研究。但利用收费数据研究行程时间可靠性较少,且已有研究在简便性、可操作性方面还有待改进。 2 行程时间可靠性定义及研究思路
本文将行程时间可靠度定义为在一定条件下,出行者由A点到达B点的行程时间小于特定时间阈值的概率,也可以理解为在一定条件下,在给定的置信水平下,出行者由A点到达B点所需要的行程时间。其基本表达公式为:
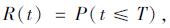
公路网络是由具有特定属性的路段和节点组成的复杂网络系统,A点与B点之间可能存在多条可行的路径,而路径可能又是由多个路段单元组成的,因此,要获得路网中任意两点间的行程时间可靠性结果,需要对问题进行分解,从研究和分析最为基本的路段行程时间分布特性及可靠性确定方法着手,进而研究路径行程时间可靠性分析方法,最后,基于路径行程时间可靠性分析方法,结合路径概率选择模式,得到路网中任意A点与B点间,也即OD对间的行程时间可靠性确定方法,这也是本文研究行程时间可靠性的思路。 3 路段行程时间可靠性建模 3.1 路段行程时间分布及统计拟合
(1)数据来源
研究所用数据为甘肃省平定高速公路西段部分收费站的收费数据,时间范围为2010年5月至8月逐日单车数据。原始数据主要包括以下字段信息:入口时间、入口站点、出口时间、出口站点、出口车道、车型、车情、客货标识、轴数、车重、ETC标识等。可以从收费数据中,提取路段行程时间信息,作为研究分析的样本。
(2)数据处理、剔除和筛选方法
① 选择路段单元。本文路段单元是指高速公路两个相邻收费站之间的路段,需要结合路段构造物和沿线设施分布,剔除存在隧道、服务区/停车区等构造物和设施的路段。
② 筛选车辆数据。设S,E分别为相邻两个互通/收费站,U为S->E方向上游互通,D为S->E方向下游互通,路段单元行程时间样本数据可能来自四种情况的数据,如表 1所示。
| 入口 | 出口 | (S->E)路段行程时间 |
| S | E | 直接提取 |
| U | E | 计算提取 |
| S | D | 计算提取 |
| U | D | 计算提取 |
③车型考虑。数据提取过程中,剔除了军车、超时车辆等部分车辆数据。依据收费数据中的车型字段,将数据分类客车与货车两类,主要是考虑客车与货车间速度差异明显,且客车和货车的实际需求也不同。
④ 天气因素。低能见度、降雨、降雪、路面冰雪等气象与路面条件对实际通行能力和行驶速度均有影响,利用公路沿线气象监测设施的监测数据,通过时间与样本数据匹配,将天气因素纳入影响变量。本研究分析样本为良好天气条件下的数据,即能见度大于500 m,无降水现象,路面无冰雪。
(3)路段行程时间统计分布拟合
① 以不同月份内的单个路段行程时间作为总体,对总体采用等距随机抽样得到数据样本,做路段行程时间的统计频率直方图,对路段行程时间的概率分布特性进行初步分析。
② 利用正态分布、伽玛分布、威布尔分布,对路段行程时间进行曲线拟合,得到路段行程时间的概率密度函数f(x)图形。
③ 利用决定系数R2、残差平方和SSE(sum of squares Error)等统计指标来衡量分布曲线的拟合效果。
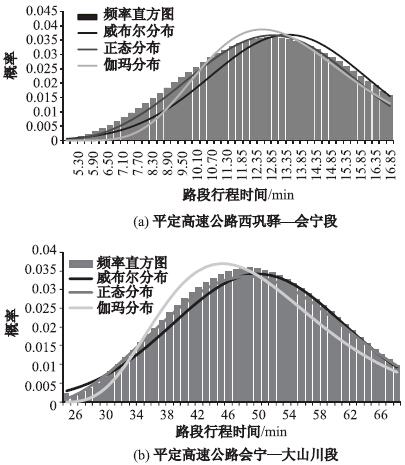
图 1为甘肃平定高速公路西段会宁所2010年5月部分路段行程时间频率直方图和统计分布拟合情况。通过SSE和决定系数R2对3种概率分布进行比较,正态分布相较于威布尔分布和伽玛分布具有更好的拟合效果,判定指标如表 2所示。
|
| 图 1 客车行程时间概率分布 Fig. 1 Probability distribution of travel time |
| 路段 |
西巩驿— 会宁 |
会宁— 大山川 |
大山川— 静宁 |
静宁— 司桥 | |
| 正态分布 | SSE | 0.005 4 | 0.006 3 | 0.012 7 | 0.003 1 |
| R2 | 0.999 8 | 0.999 8 | 0.999 7 | 0.999 9 | |
| 威布尔分布 | SSE | 0.031 0 | 0.009 6 | 0.036 5 | 0.038 3 |
| R2 | 0.999 1 | 0.999 7 | 0.999 1 | 0.999 1 | |
| 伽玛分布 | SSE | 0.023 4 | 0.029 1 | 0.025 9 | 0.023 5 |
| R2 | 0.999 3 | 0.999 0 | 0.999 4 | 0.999 4 | |
④ 为验证路段行程时间服从正态分布合理性,利用假设检验方法,对路段行程时间是否符合正态分布进行了检验。在显著性水平为0.05的条件下,临界值χ2α(DF)大于统计量χ2,通过了H0假设,具体过程从略。 3.2 路段行程时间可靠性模型
由3.1节统计分析结果可知,路段行程时间服从正态分布,因此,路段行程时间的概率密度函数可以由正态分布模型来描述,见式(1)。由概率密度函数可以得到路段行程时间的概率分布函数,即路段行程时间可靠性模型,见式(2)。
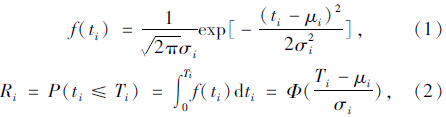
由式(2)可知,路段行程时间可靠性模型求解的关键是标定路段行程时间的期望μi和标准差σi这两个参数。采用矩估计法求解这两个参数[15]:
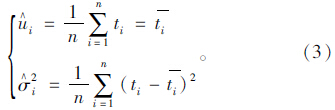
路径一般都是由多个路段单元组成,因此路径行程时间的概率分布模型为一组正态随机变量之和的函数。根据正态分布函数的性质,当随机变量服从正态分布时,正态随机变量之和也服从正态分布,即:
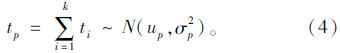
类似地,路径行程时间可靠性模型为:
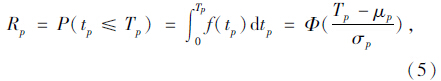
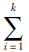 =1(ti·δi); ti为路段i行程时间,δi取0或1,当路段i在路径p上,则取l,否则取0。
=1(ti·δi); ti为路段i行程时间,δi取0或1,当路段i在路径p上,则取l,否则取0。由上可知,路径行程时间概率分布服从正态分布,路径行程时间可靠性模型求解的关键是确定路径行程时间的期望μp和标准差σp。假设路段行程时间是相互独立的,根据正态分布矩估计和数据期望的基本原理和性质[15],可以得到μp和σp的估计量:
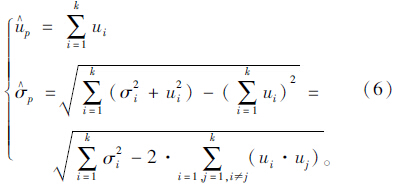
本文中第2节给出的行程时间可靠度定义在一定条件下,出行者由A点到达B点的行程时间小于特定时间阈值的概率,实质上就是指OD对间行程时间可靠性。下面探讨如何基于路径行程时间可靠性来确定OD对间行程时间可靠性。
假设OD对S,E之间包含m条有效路径,路径集合为PSE=p1,p2,…,pm,1≤j≤m,各条路径的行程时间可靠性为Rpj。根据全概率计算公式[15],OD对S,S之间的行程时间可靠性RSE为:
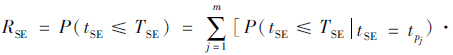
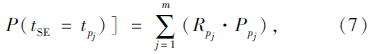
利用多项式Logit模型计算驾驶人选择路径的概率,只要能够列出OD对S,E之间的所有有效路径,并对有效路径上的实际阻抗进行计算就可以得到路径选择概率。路径阻抗可以用路径长度、行程时间、出行费用等指标来进行描述,目前广泛采用的是路径行程时间。结合实际路网拓扑结构以及可获取数据情况,采用实测路径平均行程时间来代表路径的实际阻抗值是比较合理的。对Logit基本模型加以改进,得到Logit路径选择模型如下:
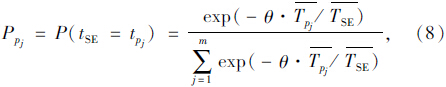
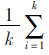 =1Ti; Ti为路径pj路段i的平均行程时间;TSE为OD对S,E之间的所有路径的平均出行阻抗,即所有路径的平均行程时间,其计算公式为:TSE=
=1Ti; Ti为路径pj路段i的平均行程时间;TSE为OD对S,E之间的所有路径的平均出行阻抗,即所有路径的平均行程时间,其计算公式为:TSE= =Tpj; θ为无量纲的分配参数,与可供选择的有效出行路径数有关。根据已有研究成果对出行者选择模型分析发现,有效出行路径数为2条时,θ取值为3.00~3.50;有效出行路径数为3条及以上时,θ取值为3.00~3.75,其取值比较稳定,因此实际应用时,θ可取3.00~3.50。
=Tpj; θ为无量纲的分配参数,与可供选择的有效出行路径数有关。根据已有研究成果对出行者选择模型分析发现,有效出行路径数为2条时,θ取值为3.00~3.50;有效出行路径数为3条及以上时,θ取值为3.00~3.75,其取值比较稳定,因此实际应用时,θ可取3.00~3.50。6 结论与展望 6.1 主要结论
提出了利用高速公路收费数据研究和建立路网中OD对间行程时间可靠性建模的方法,基于历史收费数据分析建模后,可以得到适用于本地的行程时间可靠性模型,可用于公路运营管理部门分析和研判路网运行态势,预测行程时间,为出行者制订出行计划与在途出行提示与路径诱导提供实用性的方法。
所建立的模型回答了以下几类问题:(1) 出行者由A点到达B点的行程时间小于特定时间阈值的概率;(2) 在给定的置信水平下,出行者由A点到达B点所需要的行程时间;(3) 在指定的时间内,出行者能够完成由A点到B点出行的概率等。需要指出的是,行程时间可靠性的概率模型是有条件的,均是指在特定的道路、交通、天气、事件等条件下。
具体结论如下:(1)利用高速公路收费数据,分析了路段行程事件概率分布特征,通过利用已知的多种分布拟合及分布假设检验,通常条件下路段行程时间是符合正态分布特征的;(2)基于路段行程时间符合正态分布前提,建立了路段行程时间可靠性模型,并给出了模型参数估计方法;(3)在路段行程时间可靠性模型的基础上,基于路段间的行程时间分布相互独立的假设,建立了路径行程时间可靠性模型,并给出了模型参数估计方法;(4)在路径行程时间可靠性模型的基础上,利用概率论的全概率原理和交通分配模型中的Logit路径选择模型,建立的OD对间的行程时间可靠性模型。 6.2 研究展望
本文中的路径行程时间可靠性模型是基于路段时间可靠性模型建立,前提假设是路段行程时间分布相互独立,这一假设与简化处理需要在后续研究中具体分析;由于样本量所限,本文仅针对客车在通常条件下(天气良好、无事件等)的行程时间进行了分析和建模。实际上,影响行程时间的因素涉及道路线形、交通流量及组成、限速等交通管理控制、交通事件等,且不同车型速度存在显著差异,需要在后续研究中对影响因素分类加以研究。
| [1] | ASAKURA Y,KASHIWADANI M. Road Network Reliability Caused by Daily Fluctuation of Traffic Flow[C]// Proceedings of the 19th PTRC Summer Annual Meeting. Brighton:University of Sussex,1991:73-84. |
| [2] | BELL M G H,CASSIR C,LIDA Y,et al. A Sensitivity Based Approach to Network Reliability Assessment[C]// l4th International Symposium on Transportation and Traffic Theory. Jerusalem:Elsevier,1999:283-300. |
| [3] | INOUYE H. An Evaluation of the Reliability of Travel Time in Road Network Based on Stochastic User Equilibrium[C]// Proceedings of the First International Symposium on Transportation Network Reliability. Kyoto: Pergamon Press,2001:79-91. |
| [4] | LAM W H K,XU G. A Traffic Flow Simulator for Network Reliability Assessment[J]. |
| [5] | WAKABAYASHI H. Travel Time Reliability on Expressway Network under Uncertain Environment of Snowfall and Traffic Regulation[J].Faculty of Urban Science,2004,3(3):156-160. |
| [6] | AREZOUMANDI M. Estimation of Travel Time Reliability for Freeways Using Mean and Standard Deviation of Travel Time[J]. Journal of Transportation Systems Engineering and Information Technology,2011,11 (6):75-84. |
| [7] | 裴玉龙,盖春英.公路网络运营可靠度研究[J].公路交通科技,2005,22(5):119-123.PEI Yu-long,GAI Chun-ying. Study on Operation Reliability of Highway Network[J]. Journal of Highway and Transportation Research and Development,2005,22(5):119-123. |
| [8] | 刘海旭,卜雷,蒲云.随机路网的行程时间可靠性[J].土木工程学报,2004,37(8):102-105.LIU Hai-xu,BU Lei,PU Yun. Travel Time Reliability on Stochastic Road Network[J]. China Civil Engineering Journal,2004,37(8):102-105. |
| [9] | 李先,温慧敏,高永,等.北京市路网单位距离行程时间可靠性评价[J].交通系统工程与信息,2007,7(2):72-76.LI Xian,WEN Hui-min,GAO Yong,et al. Beijing Road Network Rate Travel Time Reliability Evaluation[J]. Journal of Transportation Systems Engineering and Information Technology,2007,7(2):72-76. |
| [10] | 熊志华,姚智胜,邵春福.基于路段相关的路网行程时间可靠性[J].中国安全科学学报,2004,14(10):81-84.XIONG Zhi-hua,YAO Zhi-sheng,SHAO Chun-fu. Travel Time Reliability in Road Network Associated with Road Section [J]. China Safety Science Journal,2004,14(10):81-84. |
| [11] | 熊志华,邵春福,马社强.基于模糊感知的道路网行程时间可靠性研究[J].中国人民公安大学学报:自然科学版,2006(6):90-93.XIONG Zhi-hua,SHAO Chun-fu,MA She-qiang. Study on Travel Time Reliability of Road Network Based on Fuzzy Perception [J].Journal of Chinese People's Public Security University:Science and Technology Edition,2006 (6):90-93. |
| [12] | 陈小鸿,冯均佳,杨超.基于浮动车数据的行程时间可靠度特征研究[J].城市交通,2007,5 (5):42-45. CHEN Xiao-hong,FENG Jun-jia,YANG Chao. Research on Travel Time Reliability Characteristics Based on Floating Car Data[J]. Urban Transport of China,2007,5 (5):42-45. |
| [13] | 陈琨,于雷.基于对数正态和分布的路径行程时间可靠性模型[J].北京交通大学学报,2009,33 (3): 35-39. CHEN Kun,YU Lei. Route Travel Time Reliability Model Based on Lognormal Sum Distribution[J]. Journal of Beijing Jiaotong University,2009,33 (3): 35-39. |
| [14] | 朱彦,曹彦荣,杜道生.城市快速路行程时间的统计分析与预测[J].交通运输工程与信息学报,2009 (1): 93-97.ZHU Yan,CAO Yan-rong,DU Dao-sheng. Travel Time Statistical Analysis and Prediction for the Urban Freeway[J]. Journal of Transportation Engineering and Information,2009 (1): 93-97. |
| [15] | 盛骤.概率论与数理统计 [M].第四版.北京:高等教育出版社,2008.SHENG Zhou. Probability and Mathematical Statistics [M]. 4th ed. Beijing: Higher Education Press,2008. |
 2014, Vol. 31
2014, Vol. 31
