扩展功能
文章信息
- 李周平, 韩景倜, 杨坚争, 肖宇
- LI Zhou-ping, HAN Jing-ti, YANG Jian-zheng, XIAO Yu
- 基于分层复杂网络的城际路网空间结构特征
- Spatial Structural Characteristics of Intercity Highway Network Based on Layered Complex Network
- 公路交通科技, 2014, Vol. 31 (12): 98-103
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 98-103
- 10.3969/j.issn.1002-0268.2014.12.016
-
文章历史
- 收稿日期:2014-04-10
2. 上海理工大学 管理学院, 上海 200093;
3. 上海财经大学 信息管理与工程学院, 上海 200433
2. School of Business, University of Shanghai for Science and Technology, Shanghai 200093, China;
3. School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai 200433, China
2013年发布的《国家公路网规划(2013—2030)》指出,截至2011年底,我国公路总里程达到 4.106×106 km,其中普通国道1.06×105 km,国家高速公路6.4×104 km。但仍有900多个县没有国道连接,人口在2×105人以上的18个城市和29个地级市未与国家高速公路连接。为适应社会经济及城乡协调发展的要求,《十二五综合交通运输体系规划》提出将进一步加大城际干线公路建设力度,建成由普通国、省道干线和国家高速公路构成的连通各级城市的城际公路网络。在2030年前建成总规模约2.65×105km的普通国道路网,全面连接县级及以上行政区。建成总规模约为 1.18×105 km的国家高速路网,全面连接地级行政中心和城镇人口超过2×105 人的中等及以上城市。
城际公路网络作为城市经济联系与发展的基础条件,研究其网络结构的复杂性特征,对于认识城市经济的空间联系、优化路网结构、分析交通动力学特征具有重要意义。从Gastner和Newman将复杂网络理论应用于美国高速公路网络研究以来[1],国外学者将该理论广泛应用于城市路网结构的复杂性测度、路网可靠性及其功能特征等方面的研究[2, 3, 4]。国内学者则主要通过局部路网的复杂网络建模分析,对网络拓扑结构特征、区域经济联系和路网演化模型进行了研究[5, 6, 7, 8]。
目前国内外文献多借助高速公路路网数据,在拓扑结构基础上分析公路路网的结构与功能特征。这不仅忽略了路网要素的空间属性所蕴含的物理结构特征,也未考虑城市节点间交通运输需求对路网结构的影响。另外,完全以高速公路路网数据建立的城际公路网络结构模型忽略了普通国省道干线公路的替代效应。针对以上问题和研究现状,本文在传统复杂网络理论基础上引入GIS分析方法,提出一种反映路网空间特征与节点逻辑联系的交通网络分层结构模型,并应用于我国城际路网空间结构特征的复杂性分析中。 1 数据处理与研究方法 1.1 数据来源
本文以我国城际公路交通系统作为研究对象。依据《中国基础地理信息数据库》提供的地理坐标数据,去除台湾、海南及与我国大陆地区无高速公路、国道及省道连通的城市,提取2 212个县、市、直辖市等行政区域中心位置的平面坐标作为网络节点坐标,并根据2011年《中国区域经济统计年鉴》取得其中330个地级行政区及4个直辖市的区域生产总值(GRP)数据。对照《2010年中国公路交通地图》,去除国家高速公路、普通国道、省道重合的公路路段,共提取反映2 212个城市节点间物理连通关系的4 136条公路路段数据。考虑节点间公路交通流量多为往返流量,因此将城际路网系统处理为无向网络。 1.2 城际路网的分层模型
Kurant在其复杂网络的分层结构模型[9]中指出,现实世界中的复杂网络系统大多可以分解为彼此依存的物理层Gφ=(Vφ,Eφ)、逻辑层Gλ=(Vλ,Eλ)、映射层M(Eλ)3层结构。基于该建模思想,城际公路网络依托于城市节点和节点间的公路路段,构成了物理空间上的连通关系Gφ,往返于城市间的公路运输需求则形成了节点间的逻辑联系Gλ。公路运输需求按照最小运输时间成本的路径选择规则,在城市节点与公路路段上形成的流量负载则构成公路交通的映射关系M(Eλ)。 1.2.1 物理层网络
物理层网络Gφ可通过四元组结构{n1,n2,da,va}来表示。其中n1,n2为路段a连接的两个城市的节点;da,va分别为路段a的长度与设计时速。为简化起见,将高速公路、国道、省道的设计时速分别统一为120,80,60 km/h。如节点间同时有多条公路连接,只建立一条物理连边,va取最高设计时速。 1.2.2 逻辑层网络
考虑难以取得国内各城市节点间的公路交通的OD数据,而公路货运OD相对稳定,且与城市间的经济联系成强正相关关系[10, 11],因此本文采用威尔逊经济引力模型,计算节点间的理论货运OD强度[12],见式(1)。gr,gs分别为城市节点r,s的GRP;pr,ps分别为r,s的人口规模;drs为城市节点间的欧式距离。为简化计算,本文认为县级行政区域的公路货运需求主要在与其所属的地级行政区域之间集中产生。因此,将县级城市节点的GRP统一并入其所属的地级或直辖市节点,从而将逻辑网络节点Vλ缩减为334个。根据王铮等人[13]的实证研究结论,设定调节系数K为1,距离阻抗参数β为0.003 2,并对55 611对城市节点r,s间的理论运输需求数据ODrs进行标准化处理。
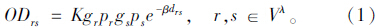
逻辑层上反映所有节点间理论运输需求的ODrs,按运输时间最小的路径选择机制完成配流,最终在物理层节点与边上形成的配流负载关系,即为映射层网络M(Eλ)。在计算过程中,某条路径的运输时间为该路径经过的所有路段的运输时间之和,其中各路段的运输时间ta=da/va。 1.3 网络结构复杂性的测度方法 1.3.1 节点运输需求强度
节点运输需求强度S(i)反映了逻辑层网络中,节点作为交通运输需求产生源的重要程度,见式(2):
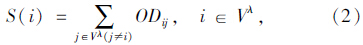
复杂网络统计方法将节点或边的介数定义为网络所有最短测地线路径中经过该节点或边的数量的比例[14]。相比节点间的测地线距离,在对公路网络物理层结构的统计分析中,两节点间的运输时间更具实际意义。因此,本文将运输时间引入介数指标,提出了节点交通介数BC(i),见式(3):
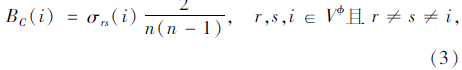
同理可计算边a的交通介数BC(a)。 1.3.3 负载介数
交通介数指标的设计是基于所有节点间运输需求等权的假设,即网络中任意两节点间的交通运输需求是相等的。但是在真实的交通运输系统中,任意两节点间的运输需求并不相同。本文在交通介数指标的基础上,提出了反映映射层网络节点或边负载程度的负载介数指标。指标值为任意两节点间的运输需求,按最小运输时间的配流规则,在节点或边上形成的OD负载量。节点的负载介数指标BL(i)见式(4),当OD节点r,s间的最小运输时间路径通过节点i时,条件概率P(r,s|i)值为1;否则P(r,s|i) 为0。同理可计算边a的负载介数 BL(a)。
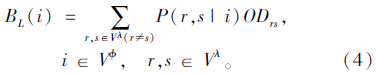
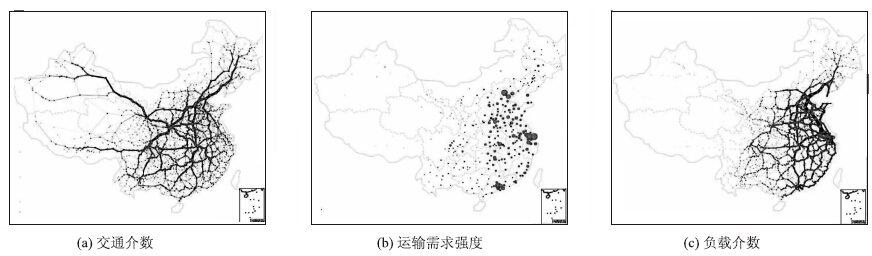
引入运输时间属性的交通介数指标,较好地反应了城际路网物理层结构在空间分布上的中心性特征。运用式(3)分别计算物理层网络2 212个节点与4 136条边的交通介数。其中交通介数值排名前20的城市见表 1。图 1(a)则揭示了节点与边交通介数值的空间分布,节点的大小与边的线宽分别表示城市与路段交通介数的相对大小。由表 1与图 1(a)可知,高交通介数的城市与路段呈明显的轴辐式分布。其中连霍高速公路的乌鲁木齐-西安段与福银高速公路的西安-武汉段,形成了贯穿西北与东南的交通介数中心线。京哈高速公路全线与途经石家庄、西安、广元、成都的京昆高速公路形成了贯穿东北与西南的交通介数中心线。而经过石家庄、郑州、武汉、广州的京珠高速公路则形成了贯穿我国南北的交通介数中心线。
| 物理层 | 逻辑层 | 映射层 | |||
| 节点和交通介数 | 节点和运输需求强度 | 节点和负载介数 | |||
| 西安 0.24 | 广元 0.12 | 上海 0.060 | 杭州 0.016 | 天津 0.113 | 郑州 0.058 |
| 石家庄 0.19 | 兰州 0.12 | 北京 0.048 | 东莞 0.015 | 无锡 0.112 | 唐山 0.057 |
| 武汉 0.19 | 汉中 0.11 | 苏州 0.047 | 合肥 0.015 | 济南 0.098 | 德州 0.057 |
| 郑州 0.15 | 长沙 0.11 | 广州 0.043 | 唐山 0.014 | 苏州 0.094 | 上海 0.056 |
| 天津 0.14 | 新乡 0.11 | 无锡 0.035 | 深圳 0.014 | 淮安 0.086 | 合肥 0.053 |
| 保定 0.14 | 秦皇岛 0.11 | 天津 0.024 | 长沙 0.011 | 南京 0.080 | 石家庄 0.051 |
| 晋中 0.13 | 锦州 0.10 | 常州 0.021 | 临沂 0.011 | 江都 0.078 | 杭州 0.051 |
| 成都 0.13 | 漯河 0.10 | 武汉 0.019 | 徐州 0.010 | 广州 0.070 | 锦州 0.048 |
| 六安 0.13 | 株洲 0.10 | 佛山 0.017 | 洛阳 0.008 | 江阴 0.067 | 北京 0.046 |
| 唐山 0.13 | 邯郸 0.10 | 郑州 0.017 | 宁波 0.008 | 武汉 0.060 | 徐州 0.044 |
|
| 图 1 路网结构测度指标的空间分布 Fig. 1 Spatial distribution of measurement indicators of road network |
城际路网物理层的空间分布相对均匀,但表现出不同层次的中心性特征。西安作为整个城际路网的交通介数中心轴,全网23.5%的最小运输时间路径都经过西安市。石家庄、兰州、成都、郑州、武汉等次级交通介数中心轴分别与我国东北、西北、西南及东部地区的城市连通。连霍、福银、京哈、京昆、京珠、沪蓉高速公路及312,102,108,107,318,307等普通国道,则作为串联这些中心轴的辐式干线公路,起到了连通各区域中心节点的关键作用。而全网70%以上的18个城市节点交通介数小于0.01,这些城市作为单边网络的终端或局部网络中心节点对城际路网整体的运输时间影响作用较小。 3 城际路网运输需求联系
3.1 需求联系的空间分布
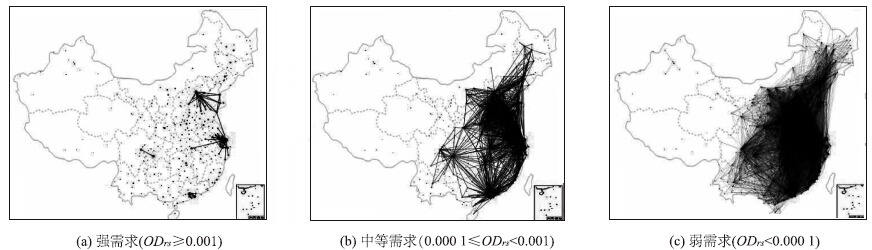
按式(1)计算逻辑层网络Gλ中334个地级以上城市节点之间的55 611对理论货运OD数据,按其强度值划分为强需求(ODrs≥0.001)、中等需求(0.000 1≤ODrs<0.001)、弱需求(ODrs<0.000 1)3种类型。3种类型的公路运输需求在城市节点间的空间分布见图 2,其中强运输需求主要分布在长三角、珠三角、环渤海、成渝等经济发达且区域聚集程度较高的地区。排序前20的强运输需求见表 2,其中上海—北京、北京—天津、广州—深圳的运输需求强度居前。中等运输需求分布区域较广,主要集中于较大规模城市之间的远距离运输。这些城市受惠于经济的规模优势,但相对较远的距离弱化了城际公路运输需求的联系,如北京—沈阳、苏州—青岛、上海—北京、广州—长沙等。弱运输需求则分布于中小规模城市之间的运输,如常州—聊城、九江—金华、衡阳—泉州、巢湖—绍兴等。
|
| 图 2 节点间的公路交通运输需求空间分布 Fig. 2 Spatial distribution of road transport demand between nodes |
| 逻辑层 | 映射层 | ||
| OD节点和运输需求强度 | 路段和负载介数 | ||
| 上海—苏州 0.005 3 | 北京—唐山 0.001 9 | 苏州—无锡 0.095 | 临沂—淮安 0.048 |
| 北京—天津 0.004 0 | 苏州—无锡 0.001 9 | 无锡—江阴 0.067 | 天津—廊坊 0.048 |
| 广州—深圳 0.003 3 | 深圳—佛山 0.001 7 | 唐山—天津 0.066 | 广州—佛山 0.047 |
| 上海—无锡 0.003 2 | 苏州—杭州 0.001 7 | 淮安—扬州 0.061 | 锦州—盘山 0.047 |
| 上海—杭州 0.003 1 | 广州—东莞 0.001 6 | 天津—沧州 0.056 | 北京—廊坊 0.046 |
| 上海—宁波 0.002 7 | 上海—常州 0.001 6 | 江阴—扬州 0.055 | 唐山—秦皇岛 0.044 |
| 上海—南京 0.002 2 | 上海—天津 0.001 5 | 沧州—德州 0.055 | 南京—溧阳0.043 |
| 广州—佛山 0.002 2 | 深圳—东莞 0.001 4 | 上海—苏州 0.053 | 济南—莱芜 0.042 |
| 北京—上海 0.002 1 | 北京—大连 0.001 4 | 济南—德州 0.053 | 锦州—葫芦岛 0.041 |
| 上海—南通 0.001 9 | 北京—青岛 0.001 4 | 新泰—临沂 0.050 | 苏州—吴江 0.040 |
应用式(2)分别计算逻辑层网络节点的运输需求强度S(i)值排名前20的城市节点(见表 1)。从图 1(b)来看,城市节点间运输需求强度的空间分布与交通介数对称的轴辐式分布不同,总体来看其存在明显的东西差异。以京哈高速与京珠高速这两条贯穿我国南北的高速公路为界,运输需求强度较高的城市节点主要集中在该条界限以东的地区。该界线以东(含该界限)的中东部地区共148个地级及直辖市节点,其运输需求强度总量占整个网络的76%,而该界限以西的187个地级及直辖市节点的占比仅为24%。究其原因,主要是该界限东西区域的经济规模与公路交通成本存在明显差异。中东部地区这148个城市2011年公布的GRP总值为2.346 52×1013元,该区域148个节点之间通过公路网络的平均到达时间为9.7 h。而西部地区187个城市2011年公布的GRP总值仅为1.339 12×1013元,该区域的187个节点间通过公路网络的平均到达时间为16.3 h。 3.2 运距分布
对理论货运OD数据的运输距离统计分析发现,我国地级以上城市之间的公路运距的平均值为697 km,其中运距小于200 km的短途运输占总量的13.5%,运距在200~1 000 km之间的中途运输需求量所占比例为63%,1 000~2 000 km的长途运输需求量占比为22.5%,而大于2 000 km的运输需求仅占比1%。该统计结果与杨铭等人[15]通过真实货运OD数据的实证研究结论相一致,进一步说明本文在计算我国城际公路货运需求时所采用的理论模型及参数设定是合理的。 4 城际路网交通负载 4.1 交通负载的空间分布
城际公路的映射层网络,是在城市节点间的运输需求与物理连通关系的共同作用下,所形成的反映网络系统节点与边负载关系的映射结构。通过式(4)计算映射层网络节点与边的负载介数。表 1与表 2分别列举了负载介数值排名前20的城市节点与公路路段,图 1(c)则反映了映射层网络节点与边的负载介数值的空间分布。
从负载介数的空间分布分析看,负载中心线呈两纵两横的空间分布形态。沿京哈高速、京台高速、京沪高速公路形成的串联锦州、秦皇岛、唐山、天津、北京、济南、淮安、苏州、无锡、上海等高负载介数城市的环渤海、长三角和京沪沿线负载中心线,其负载介数的中心性程度最高。另一条贯穿我国中部地区主要城市的京珠高速公路,则形成了连接北京、石家庄、郑州、武汉、长沙、广州等高负载介数节点的纵向负载中心线。而由沪蓉高速公路及连霍高速公路西安—徐州段形成了连接上海、南京、武汉、成都及西安、郑州、徐州等城市的横跨我国东西部地区的两条横向负载中心线。 4.2 交通负载的功能特征
从节点与公路路段承担交通负载的功能特征来看,高负载介数城市及公路路段主要分为两类:一类主要分布在环渤海、长三角、珠三角等经济发达且区域聚集程度较高的地区,这一类城市如北京、天津、唐山、上海、苏州、无锡、南京、广州、深圳、佛山,作为公路运输需求的源节点或目的节点,其本身的运输需求强度较高,而连接这些城市的高负载公路路段主要承担了较短运距的区域性运输功能,如杭州湾环线、珠三角环线、常台、日兰、京沪高速公路。另一类城市如济南、石家庄、徐州、郑州、武汉、西安、合肥、淮安,作为交通枢纽中转节点,其交通介数值较大,而连接这些节点的高负载公路主要为承担跨区域运输功能的干线公路如连霍、福银、京珠、沪渝、青银高速公路。 5 结论
在考虑空间位置属性与运输需求对网络结构特征影响作用的基础上,本文结合分层复杂网络模型,提出了交通介数、运输需求强度、负载介数等路网结构测度指标,并应用于我国内地城际路网的空间结构分析,得出如下结论:
(1)节点及边的交通介数分布以西安为轴中心,以连霍、福银、京哈、京昆、京珠、沪渝、青银高速公路及312,102,108,107,318,307等普通国道干线公路为辐,形成了向石家庄、武汉、郑州、成都、兰州5个次级中心成放射性分布的轴辐式交通介数中心线。(2)公路交通需求联系在空间分布上呈现出明显的区域特征与地区差异。强需求联系主要集中在以北京、上海、广州为中心的环渤海、长三角、珠三角地区。由于经济规模的聚集效应与公路运输时间成本因素的作用,城市节点的运输强度分布以京哈高速公路与京珠高速公路为界表现出明显的东强西弱的地区差异。(3)在强运输需求作用下,负载分布在环渤海、长三角及京沪高速公路沿线城市,形成了明显的区域中心性特征。在中等及弱运输需求作用下,交通介数较高的济南、石家庄、徐州、郑州、武汉等城市,作为公路交通的中转枢纽城市也具有较高的负载。
| [1] | GASTNER M T, NEWMAN M E J. The Spatial Structure of Networks [J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2006. 49(2): 247-252. |
| [2] | XIE F, LEVINSON D. Measuring the Structure of Road Networks [J]. |
| [3] | JENELIUS E, PETERSEN T, MATTSSON L. Importance and Exposure in Road Network Vulnerability Analysis [J]. |
| [4] | HU Y, ZHU D. Empirical Analysis of the Worldwide Maritime Transportation Network[J]. |
| [5] | 周恺. 长江三角洲高速公路网通达性与城镇空间结构发展[J]. 地理科学进展, 2010. 29(2): 241-248.ZHOU Kai. Expressway Network Accessibility Analysis and Structured Change of Urban System in Yangtze Delta Megalopolis[J]. Progress in Geography, 2010, 29(2): 241-248. |
| [6] | 杨成凤, 韩会然. 皖江城市带区际公路交通空间组织研究[J]. 经济地理, 2013. 33(3): 65-72.YANG Cheng-feng, HAN Hui-ran. Study on Interregional Road Traffic Spatial Organization in the Cities along the Yangtze River in Anhui Province[J]. Economic Geography, 2013, 33(3): 65-72. |
| [7] | 沈鸿飞, 贾利民, 王笑京,等. 基于公路网结构特性的关键节点评价指标与辨识方法[J]. 公路交通科技, 2012.29(9):137-142.SHEN Hong-fei, JIA Li-min, WANG Xiao-jing, et al.Evaluation Indexes and Identification Method of Key Nodes Based on Structural Characteristics of Road Network[J]. Journal of Highway and Transportation Research and Development, 2012,29(9):137-142. |
| [8] | 李周平, 韩景倜. 基于空间引力作用的复杂网络演化模型[J]. 计算机应用研究, 2011, 28(7):2625-2627, 2631.LI Zhou-ping, HAN Jing-ti.Modeling Evolution of Complex Networks Based on Spatial Gravitation[J]. Application Research of Computers, 2011, 28(7):2625-2627, 2631. |
| [9] | KURANT M, THIRAN P. Layered Complex Networks[J]. |
| [10] | JUNG W S, WANG F, STANLEY H E. Gravity Model in the Korean Highway[J]. Europhysics Letters, 2008, 81(4): 4805-4820. |
| [11] | 何远成, 李芳, 胡玉洲,等. 基于货运量引力模型的流域物流网络结构研究: 以珠江为例[J]. 物流技术, 2013, 32(3): 315-318.HE Yuan-cheng, LI fang, HU Yu-zhou, et al.Study on Structure of Watershed Logistics Network Based on Freight Volume Gravity Model: In the Case of Zhujiang [J]. Logistics Technology, 2013, 32(3): 315-318. |
| [12] | WILSON A G. Entropy in Urban and Regional Modeling[M]. London: London Pion, 1970. |
| [13] | 王铮. 理论经济地理学[M]. 北京: 科学出版社, 2002.WANG Zheng. Theoretical Economic Geography [M]. Beijing: Science Press, 2002. |
| [14] | FREEMAN L C. A Set of Measures of Centrality Based on Betweenness[J]. |
| [15] | 杨铭, 秦华容. 公路货运平均运距分析与实证研究[J]. 物流技术, 2009,28(6): 22-24, 49.YANG Ming, QING Hua-rong.Field Survey and Analysis on Average Transport Distance of Road Freight[J]. Logistics Technology, 2009, 28(6): 22-24, 49. |
 2014, Vol. 31
2014, Vol. 31
