扩展功能
文章信息
- 吕慎, 田锋, 莫一魁
- LÜ Shen, TIAN Feng, MO Yi-kui
- 轨道交通枢纽地铁换乘接运公交乘客平均候车时间研究
- Average Waiting Time of Passengers Transferring from Subway to Feeder Bus at Rail Transit Hub
- 公路交通科技, 2014, Vol. 31 (12): 92-97
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 92-97
- 10.3969/j.issn.1002-0268.2014.12.015
-
文章历史
- 收稿日期:2014-01-08
2. 深圳城市交通规划设计研究中心有限公司, 广东 深圳 518031
2. Shenzhen Urban Transportation Planning Center Co., Ltd., Shenzhen Guangdong 518031, China
轨道交通枢纽地铁与接运公交间换乘乘客平均候车时间是制订和优化接运公交运营调度策略和方案,评估地铁与接运公交一体化运营水平的重要指标,直接决定公交乘客出行的连续性、可靠性和舒适性,影响公交系统的吸引力和对小汽车交通方式的竞争力。
当前,对接运公交与轨道交通协调调度优化方面进行了大量地研究。Lee[1, 2]和Schonfeld[3]建立了协调调度发车间隔优化的方法;Shoaib[4]进一步拓展到轨道交通线路为主轴线的公共交通系统的协调调度,按此思路,张宇石[5]、陈旭梅[6]、何波[7]、滕靖[8]对轨道交通与常规公交之间的协调调度发车间隔优化进行了研究。在上述这些研究中,换乘乘客的平均候车时间主要采用的是Welding的公式[9]:
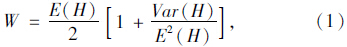
由于公式(1)是针对一般站点候车乘客建立,且需要满足以下假定:乘客的到站服从均匀分布,乘客总是可以乘坐第一辆车离开。但是,当前关于换乘乘客到站分布规律的研究不支持其服从均匀分布的结论[10, 11, 12]。由此利用公式(1)计算换乘乘客平均候车时间可能与实际存在较大偏差,因此,有必要基于换乘乘客的实际到站分布研究换乘乘客的平均候车时间。S.K. Jason Chang[13]基于接运公交换乘乘城际轨道交通乘客到站行为规律的分析,建立了接运公交换乘城际轨道交通的乘客平均候车时间模型。郭淑霞[11]通过实地调查,将北京市地铁13号线换乘公交的乘客分为固定客流和随机客流分别确定其到站分布模型,并建立换乘乘客平均候车时间模型。综上所述,当前换乘乘客平均候车时间的研究相对较少,更多的是借用一般站点公交乘客的研究成果,且少量的关于换乘乘客平均候车时间研究都是针对特定类型的或者某个具体的换乘枢纽,缺乏对轨道交通枢纽内轨道交通与接运公交运营特性、换乘乘客行为与平均候车时间的关系的深入和系统性的研究。
因此,本文在深入剖析影响换乘乘客平均候车时间影响因素的基础上,建立换乘乘客平均候车时间模型,并系统地研究在上述影响因素变化的条件下,换乘乘客平均候车时间的变化规律,为制订和优化接运公交调度方案提供科学、合理的依据。 1 换乘乘客平均候车时间主要影响因素
由于轨道交通可靠性高,且对地铁系统而言,其发车间隔一般在5 min左右,接运公交换乘地铁的乘客候车时间一般较短。相对而言,接运公交发车间隔较长且可靠性差,即使接运公交的发车频率较高,也存在换乘乘客候车时间很长的问题。因此,换乘出行效率低下的问题集中地表现为地铁换乘接运公交。因此,本文以地铁换乘接运公交的乘客为研究对象,其平均候车时间主要受换乘乘客到站时间分布、接运公交发车间隔、接运公交发车时刻和接运公交运营可靠性等因素的综合影响。
(1)换乘乘客到站时间分布
轨道交通枢纽内地铁换乘接运公交的乘客可以分为两类,一类是地铁下车后直接换乘接运公交的乘客,另一类是地铁下车后,在枢纽站内进行了购物、简单餐饮等活动之后再换乘接运公交的乘客,从目前的调查的结果来看,尤其是早、晚高峰期,直接换乘乘客的比例高达90%以上[11]。因此,本文采用直接换乘乘客作为换乘乘客到站时间分布。依据当前的研究成果可以认为直接换乘乘客到站时间分布服从正态分布[10, 11, 12]。即:
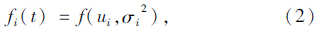
(2)接运公交的发车间隔
为了利用先进的公共交通系统(Advanced Public Transport System,APTS)实现接运公交与轨道交通的协调调度,以减少换乘乘客的候车时间,接运公交的发车间隔通常取轨道交通的整数倍(一般不超过3)[1, 2, 3]。

(3)接运公交发车时刻
由于换乘乘客在枢纽内个体行为上的差异,换乘乘客到达站点的时间是随机的。因此,即使接运公交采用相同的发车频率和运营可靠性,如果其发车时刻不同的话,换乘乘客平均候车时间也有很大的差异。
(4)接运公交运营可靠性
接运公交运营可靠性直接决定换乘乘客实际的候车时间。现时接运公交的调度主要控制发车频率,本文采用接运公交车头时距的方差和发车间隔比值描述接运公交的可靠性的高低。

综上所述,换乘乘客平均候车时间是上述四因素综合作用的结果。其中换乘乘客到站时间分布属于换乘乘客行为方面的因素,接运公交发车间隔、发车时刻以及接运公交运营可靠性属于接运公交运营调度方面的因素。 2 换乘乘客平均候车时间模型
首先假定的理想运营情况条件为:接运公交与轨道交通发车间隔相同,即Hb=Hs;接运公交车头时距的方差σH=0。基于换乘乘客到站时间服从正态分布,当接运公交处于不同的发车时刻时,建立换乘乘客平均候车时间模型。
(1)换乘乘客平均候车时间模型
第i辆地铁换乘接运公交乘客到站时间符合正态分布如图 1所示,由于接运公交与轨道交通发车间隔相同,即Hb=Hs=H,建立第i辆地铁换乘接运公交乘客平均候车时间模型为:
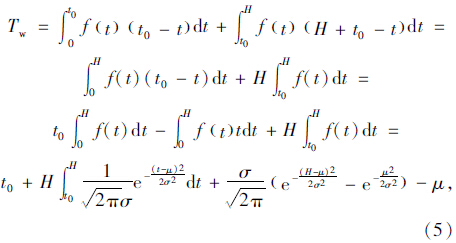
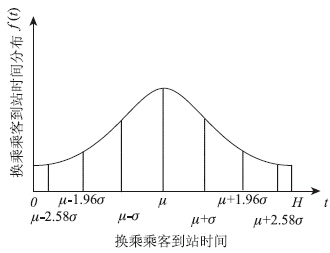
|
| 图 1 换乘乘客到站时间正态分布图 Fig. 1 Normal distribution of transfer passengers' arriving time |
(2)换乘乘客平均候车时间的变化规律
对上述换乘乘客平均候车时间模型取一阶偏导,可以确定换乘乘客平均候车时间取极值时的接运公交发车时刻。
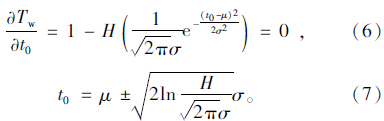
当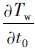 >0,即t0>μ+
>0,即t0>μ+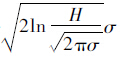 或t0<μ-
或t0<μ-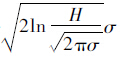 ,Tw为增函数;
,Tw为增函数;
当
当
因此,可以确定换乘乘客平均候车时间随发车时刻的变化规律如图 2所示,其中发车时刻为t0=
以下分析换乘乘客平均候车时间处于最大值和最小值时接运公交的发车时刻与正态分布特征点(μ±2.58σ,μ±1.96σ,μ±σ和μ)间的位置关系。通常接运公交的发车间隔一般在3~10 min,在无缝换乘的枢纽内,换乘步行距离一般不超过10 min,换乘乘客到站时间的标准差一般不超过5 min(尤其是高峰时段)。基于上述现状比较公式(6)确定的t0和正态分布特征点的大小,平均候车时间取最大值和最小值时t0分别位于区间μ-1.96σ,μ和区间μ,μ+1.96σ。进一步分析,可以确定若接运公交发车间隔较大,换乘乘客到站时间方差较小,则t0位于区间μ-1.96σ,μ-σ和区间μ+σ,μ+1.96σ;若接运公交间隔较小,换乘乘客到站时间方差较大,则t0位于区间μ-σ,μ和区间μ,μ+σ。
以深圳市为例,通常高峰时段Hb=Hs=H=5,且通过地铁换乘枢纽换乘乘客到站时间分布规律的调查,换乘乘客到站时间均值取μ=H/2=2.5;由于乘客步行速度的差异不是很大,相应地换乘乘客到站时间的方差也不大,一般小于均值的一半,本文以σ/μ=0.35为例,分析换乘乘客平均候车时间随接运公交发车时刻的变化规律,具体如表 1所示。
从表中结果可以发现:(1)换乘乘客平均候车时间与利用welding公式计算乘客平均候车时间存在较大差异,因为在σH=0的前提下,利用公式(1),计算其平均候车时间为2.5 min。因此,利用Welding公式计算换乘乘客平均候车时间存在较大偏差。(2)接运公交不同的发车时刻对于换乘乘客平均候车时间有较大的影响,其最大值和最小值之间相差1.8 min,因此,应改变当前仅注重接运公交发车间隔优化的做法,发车时刻优化应成为接运公交协调调度优化的重要内容。3 敏感性分析
换乘乘客平均候车时间受换乘乘客到站时间分布、接运公交与轨道交通的发车间隔以及接运公交运营可靠度的等因素的综合影响。因此,以下研究当上述因素发生变化时,换乘乘客平均候车时间的变化规律。
(1)换乘乘客到站时间分布的敏感性
在换乘乘客到站时间符合正态分布的前提下,换乘乘客到站时间的均值和方差是影响换乘乘客平均候车时间的关键因素。以上例数据为基准,当换乘乘客到站时间的均值和方差发生变化时候,换乘乘客平均候车时间的变化率如图 3和图 4所示。
从图 3中可以发现:换乘乘客平均候车时间(最大值和最小值)随换乘乘客到站时间均值的增大而增大,减少而减少,但相对于均值的变化率而言,换乘乘客到站时间平均候车时间的变化率较小。当均值变化率在±20%时,平均候车时间变化率不超过±2%,基本可以忽略。因此,可以不考虑乘客到站时间均值的变化对换乘乘客平均候车时间的影响。从图 4可以发现:换乘乘客平均候车时间的最大值变化率与换乘乘客到站时间方差变化率成反比,与之相反,其最小值变化率与方差的变化率成正比,且平均候车时间最小值变化率随方差变化率的斜率要大于最大值随方差变化率的斜率。由于方差对平均候车时间的影响大于均值对平均候车时间的影响,因此,通常不能忽略换乘乘客到站时间方差的波动对换乘乘客平均候车时间的影响。
(2)接运公交发车间隔的敏感性
换乘乘客平均候车时间模型(公式5)假定条件之一为:Hb=Hs=H。以下分析接运公交发车间隔Hb为2H或3H时,换乘乘客平均候车时间的变化规律。
当Hb=2H时:
假定接运公交发车间隔为H时,换乘乘客平均候车时间为Tw,H,μ和σ的取值同上例,则接运公交发车间隔为2H和3H时,换乘乘客平均候车时间如图 5所示。从图 5中可以发现:换乘乘客平均候车时间的增加明显大于接运公交发车间隔的增加,发车间隔增加一倍,平均候车时间要增加2倍多,因此应尽量采用与轨道交通相同的发车间隔,而不是整数倍。
(3)接运公交可靠度的敏感性
按照上文中论述的接运公交可靠度,分别取不同的接运公交车头时距方差与发车间隔比值σH/H,以σH/H=0时换乘乘客平均候车时间为基准,研究换乘乘客平均候车时间随可靠度的变化,具体如图 6所示。
从图 6可以发现,当接运公交运营由可靠(σH=0)转为不可靠(σH≠0)时,换乘乘客平均候车时间有明显的增加,并随着运营可靠性的降低,平均候车时间增加,但增加的幅度降低。因此,接运公交运营调度重要工作之一是应尽可能保证接运公交运营的可靠性。
4 结论
本文通过对换乘乘客平均候车时间影响因素的分析,基于换乘乘客到站时间符合正态分布,建立了换乘乘客平均候车时间模型,由该模型计算出的换乘乘客平均候车时间与Welding公式确定的平均候车时间有很大的差异。应用微分理论,绘出平均候车时间随接运公交发车时刻变化关系曲线,发现接运公交发车时刻是影响平均候车时间的关键因素,且存在使得平均候车时间最小的发车时刻。接着研究平均候车时间随主要影响因素变化的敏感性,结果表明:(1)平均候车时间受换乘乘客到站时间均值影响很小,基本可以忽略,但随方差变化较大;(2)平均候车时间增大倍数超过接运公交发车间隔的增大倍数的2倍;(3)当接运公交运营由可靠(σH=0)转为不可靠(σH≠0)时,换乘乘客平均候车时间有明显的增加,并随着运营可靠性的降低,平均候车时间增加,但增加的幅度降低。
综上所述,当前简单采用Welding公式计算换乘乘客平均候车时间有很大的误差,应基于换乘乘客到站时间分布建立合理的平均候车时间模型,从而保证接运公交调度方案制定和优化的科学性;应改变当前仅注重发车间隔优化而忽视发车时刻优化的做法,发车时刻优化应成为接运公交调度优化重要内容;在配车数足够的前提下,应尽可能采用与接运公交相同的发车间隔,同时注重提高接运公交运营可靠性。以上研究成果可以为接运公交调度和优化提供方向和决策依据。
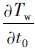 <0,即μ-
<0,即μ-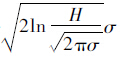
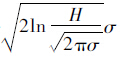 ,Tw为减函数;
,Tw为减函数;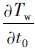 >0,即t0>μ,Tw为凸函数;
>0,即t0>μ,Tw为凸函数;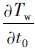 <0,即t0<μ,Tw为凹函数。
<0,即t0<μ,Tw为凹函数。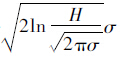 时,换乘乘客平均候车时间取最大值;发车时刻为t0=μ+
时,换乘乘客平均候车时间取最大值;发车时刻为t0=μ+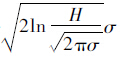 ,换乘乘客平均候车时间取最小值。因此,合理优化接运公交发车时刻,可以使得换乘乘客平均候车时间最小。
,换乘乘客平均候车时间取最小值。因此,合理优化接运公交发车时刻,可以使得换乘乘客平均候车时间最小。
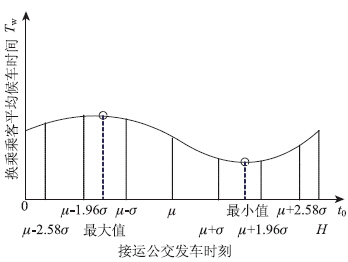
图 2 SCB试验原理图
Fig. 2 Principle diagram of SCB test
正态分布特征点 0.5%换乘乘客
到站时刻2.5%换乘乘客
到站时刻候车时间为
最大值的时刻16%换乘乘客
到站时刻50%换乘乘客
到站时刻84%换乘乘客
到站时刻候车时间为最小
值的时刻97.5%换乘乘
客到站时刻99.5%换乘乘客
到站时刻
接运公交发车时刻距离地铁到站时刻的时间 0.243 0.785 1.38 1.625 2.5 3.375 3.62 4.215 4.758
平均候车时间 2.739 3.181 3.418 3.343 2.511 1.678 1.616 1.841 2.28
注:0.5%,2.5%,16%,50%,84%,97.5%和99.5%换乘乘客到站时刻分别对应为μ-2.58σ,μ-1.96σ,μ-σ,μ,μ+σ,μ+1.96σ,μ+2.58σ
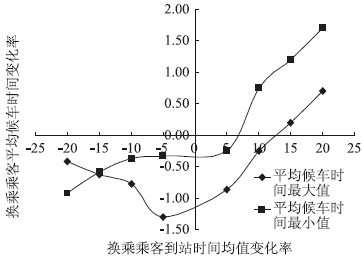
图 3 平均候车时间随均值变化关系图(单位:%)
Fig. 3 Average waiting time varying with average value(unit:%)
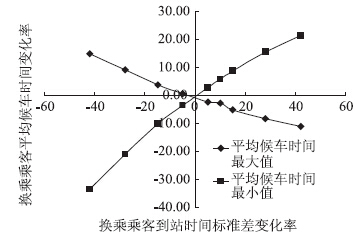
图 4 平均候车时间随方差变化关系图(单位:%)
Fig. 4 Average waiting time varying with variance(unit:%) 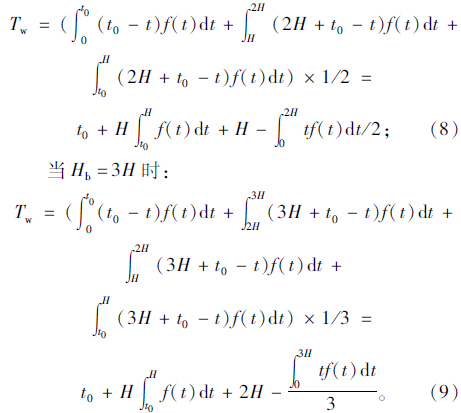
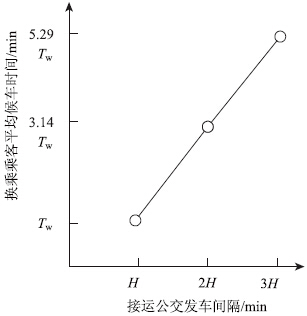
图 5 平均候车时间随发车间隔变化关系图
Fig. 5 Average waiting time varying with
departure interval
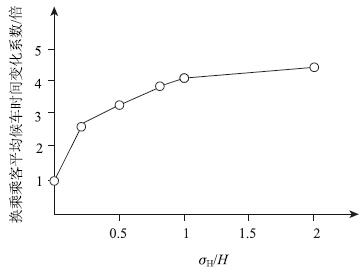
图 6 平均候车时间随发车间隔变化关系图
Fig. 6 Average waiting time varying with
departure interval
| [1] | LEE K K T, SCHONFELD P. Optimal Slack Time for Timed Transfers at a Transit Terminal [J]. |
| [2] | LEE K K T, SCHONFELD P. Real-time Dispatching Control for Coordinated Operation in Transit Terminals [J]. Transportation Research Record,1994,1433:3-9. |
| [3] | SCHONFELD P. Optimization of Timed Transfers in Transit Terminals [D]. Washington, D.C.: University of Maryland,1993. |
| [4] | SHOAIB C M,CHIEN S I. Optimization of Transfer Coordination for Intermodal Transit Networks [C/CD]// The 80th Annual Meeting of Transportation Research Board.Washington, D.C.:TRB,2001. |
| [5] | 张宇石,陈旭梅,于雷,等.基于换乘站点的轨道交通与常规公交运营协调模型研究 [J].铁道学报,2009,31 (3):11-19. ZHANG Yu-shi,CHEN Xu-mei,YU Lei,et al. Study on Model of Coordinated Operation between Urban Rail and Bus Systems at Transfer Stations [J]. Journal of the China Railway Society,2009,31 (3):11-19. |
| [6] | 陈旭梅,林国鑫,于雷.常规公共交通与轨道交通运营调度协调模型 [J].系统工程理论与实践,2009,29 (10):165-173.CHEN Xu-Mei,LIN Guo-Xin,YU Lei. Modeling Operation Scheduling Coordination between Urban Rail System and Bus System [J]. Systems Engineering-Theory & Practice,2009,29 (10):165-173. |
| [7] | 何波.城市轨道交通与常规公交运营协调优化技术研究[D].北京:北京交通大学,2009.HE Bo. Study on Coordinated Optimization of Urban Rail Transit and Bus Service [D]. Beijing:Beijing Jiaotong University, 2009. |
| [8] | 滕靖,杨晓光.APTS下城市公交枢纽调度问题的实用优化方法研究 [J].系统工程,2004,22 (8):78-82. TENG Jing,YANG Xiao-guang. A Study on Optimizing Method for Dispatching Problem of Public Transit Hub under the Condition of APTS [J]. Systems Engineering,2004,22 (8):78-82. |
| [9] | WELDING P I. The Instability of Close Interval Service [J]. |
| [10] | 常丹.地铁行人微观行为参数量化研究[D].北京:北京交通大学,2010.CHANG Dan. Quantified Study of Parameters of Microscopic Pedestrian Behavior in Subway [D]. Beijing:Beijing Jiaotong University,2010. |
| [11] | 郭淑霞,陈旭梅,于雷,等. 轨道交通换乘常规公交平均候车时间模型[J]. 交通运输系统工程与信息,2010,10(2):143-147. GUO Shu-xia,CHEN Xu-mei,YU Lei,et al. Average Waiting Time Model for Transfer from Rail Transit to Buses [J]. Journal of Transportation Systems Engineering and Information Technology,2010,10 (2):143-147. |
| [12] | 吕慎,田峰. 轨道交通枢纽换乘乘客到站时间均值特征的研究 [J]. 交通标准化,2013 (21):21-25.LÜ Shen,TIAN Feng. Means Characteristics of Transfer Passenger Arrival Time at Rail Transit Station [J]. Transportation Standardization,2013 (21):21-25. |
| [13] | CHANG S K J, HSU Chun-Lin. The Modeling of Passenger Waiting Time for an Intermodal Transit Station [C]//The 80th Annual Meeting of Transportation Research Board. Washington, D. C.:TRB, 2001: 69-79. |
 2014, Vol. 31
2014, Vol. 31
