扩展功能
文章信息
- 桂水荣, 刘律, 万水, 陈水生
- GUI Shui-rong, LIU LÜ, WAN Shui, CHEN Shui-sheng
- 简化建模方法对空心板桥力学性能的影响
- Effect of Simplified Modeling Method on Mechanical Performance of Hollow Slab Bridge
- 公路交通科技, 2014, Vol. 31 (12): 50-57,66
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 50-57,66
- 10.3969/j.issn.1002-0268.2014.12.009
-
文章历史
- 收稿日期:2014-03-11
自20世纪50年代以来,装配式预应力混凝土空心板桥在我国得到了广泛的应用[1]。目前,研究企口缝式装配式空心板桥的活载效应时,常采用忽略桥面铺装作用的铰接板法[2]、或精确的企口缝混凝土有限元模型研究空心板桥空间受力行为[3],铰接板法忽略了混凝土企口缝对横向连接的影响,而精确有限元模型过于复杂,不利于推广运用。陈记豪[4]基于铰接板梁法,研究了不同材料、截面的空心板桥汽车荷载横向分布求解问题;葛俊颖[5]研究了梁格法分析铰接板梁法的虚拟横梁刚度取值,解决了空心板桥企口缝混凝土对横向刚度的影响及计算可行问题;同时,国内学者[6, 7, 8]认为空心板桥的桥面铺装类型及质量显著影响主梁受力性能,分析空心板桥空间受力时需考虑桥面铺装的影响。研究汽车荷载对空心板桥的冲击效应,文献[9]考虑桥面铺装的影响,采用铰接板桥有限元模型研究汽车荷载对空心板桥的动力响应,忽略了空心板横向连接刚度的影响。本文以一座3跨20 m装配式预应力混凝土简支空心板桥为研究背景,建立空心板桥三维铰接梁模型和梁壳组合模型,根据实测与数值计算,对比分析空心板桥动力特性、静载响应及车桥耦合振动响应,提出适于研究空心板桥静、动力响应的有限元方法。
1 工程概况
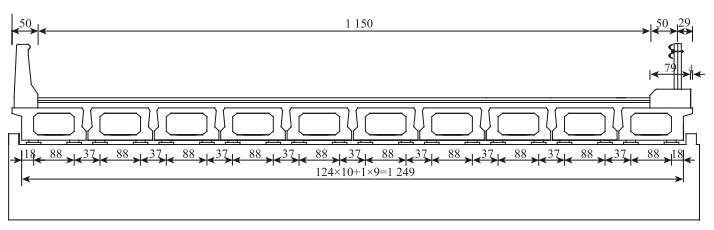
位于江西奉铜高速公路某三跨装配式预应力混凝土简支空心板桥,单幅桥由10片空心板组成,空心板高0.95 m,宽1.24 m,跨径布置为(20+20+20)m,桥梁全长64.4 m。横向布置:0.5 m(防撞栏)+11.5 m(行车道)+0.83 m(隔离带)。桥面铺装层采用4 cm厚改性沥青混凝土抗滑层+6 cm 厚中粒式改性沥青混凝土+3层FYT-1改性防水层+10 cm厚C50混凝土桥面铺装层。下部结构采用桩柱式桥墩,肋式桥台,嵌岩桩基础。设计荷载为公路-I级,横断面图如图 1所示。
|
| 图 1 空心板梁桥横截面布置示意图(单位:cm) Fig. 1 Schematic diagram of cross-section layout of hollow slab beam bridge (unit: cm) |
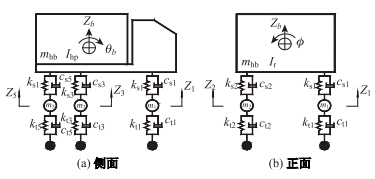
考虑动载试验需要,选取三轴自卸汽车作为研究对象。根据汽车结构特性,车辆模型简化为车体、钢板弹簧悬架支撑系统、车轴和轮胎。考虑车体竖向振动、纵向点头、侧翻以及车轮的振动特性,车辆模型简化为三维九自由度振动体系,车辆结构尺寸及动力特性参数与文献[10]一致。车辆模型见图 2。
|
| 图 2 车辆模型 Fig. 2 Vehicle model |
根据达朗贝尔原理,建立车辆振动方程:
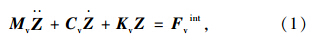
(1)梁壳组合有限元模型
根据空心板桥结构特点,空心板截面采用plan82单元进行划分,并用beam44单元模拟空心板,空心板梁纵向每米一个单元,主梁采用与企口缝混凝土刚度等效的横梁刚接;桥面铺装现浇混凝土采用shell63板单元模拟,不考虑桥面铺装层及面层沥青混凝土对横向连接刚度的影响(因沥青混凝土弹性模量较C50砼弹性模量小一个数量级),仅以质量单元分摊至全桥各节点空心板。主梁截面的预应力钢筋及普通钢筋对截面刚度的影响,通过换算截面弹性模量进行考虑,运用ANSYS建立空心板桥三维空间梁壳组合有限元模型,全桥有限元模型如图 3所示。

|
| 图 3 梁壳组合有限元模型 Fig. 3 Beam and shell composite FE model |
(2)铰接梁有限元模型
空心板截面采用plan82单元进行划分,纵向采用beam44单元模拟空心板梁,每米一个单元。主梁横向铰接,运用ANSYS建立空心板桥铰接梁有限元模型。与梁壳组合模型一致,钢筋对截面刚度的影响,通过换算截面弹性模量予以考虑。桥面铺装的层、面层及底层现浇混凝土均不考虑刚度影响,仅以质量单元分摊至全桥各节点,铰接梁有限元模型如图 4所示。

|
| 图 4 铰接梁有限元模型 Fig. 4 Hinged girder FE model |
对空心板桥进行模态分析,可得空心板桥各阶振型和频率,根据振型分解法及振型规格化,桥梁竖向和扭转运动可分别示为:
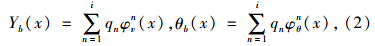
模态空间取r阶模态,桥梁结构振动方程可以写成
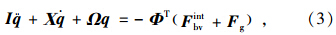
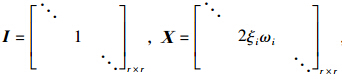
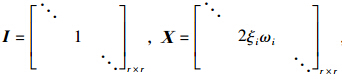 ,
式中,Φ为r阶振型向量矩阵;ξi为第i阶阻尼比;ωi为第i阶自振频率;q为振型广义坐标列阵。
,
式中,Φ为r阶振型向量矩阵;ξi为第i阶阻尼比;ωi为第i阶自振频率;q为振型广义坐标列阵。2.3 桥面不平顺激励
路面不平顺的模拟,采用三角级数叠加法模拟,桥面不平顺样本按下式产生[11]:
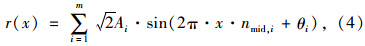
2.4 车-桥耦合模型
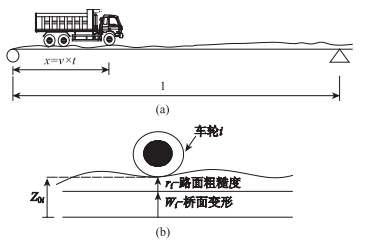
将车辆与桥梁视为整体系统,考虑车辆与桥梁空间相互作用关系,假设车轮与桥面始终保持不脱离,车辆与桥梁通过车轮与桥面接触处的位移协调和相互作用力平衡条件相联系,车辆荷载与桥面板接触如图 5所示,考虑桥面不平顺的影响,车辆与桥面接触如图 6所示,第i个车轮与桥梁之间相互作用力可示为[12]:
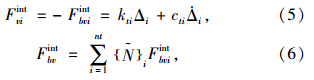
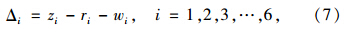
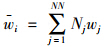 为j节点形函数; wj为i车轮处位移量;ri为i车轮处的桥面不平顺幅值。
为j节点形函数; wj为i车轮处位移量;ri为i车轮处的桥面不平顺幅值。
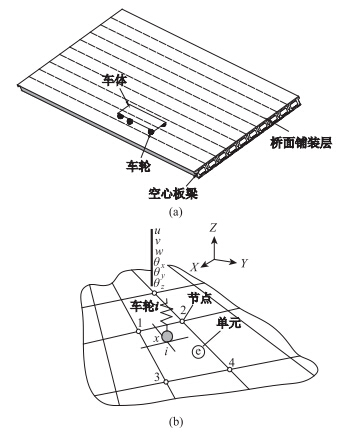
|
| 图 5 车辆荷载与桥面板单元接触示意图 Fig. 5 Schematic diagram of interaction between bridge deck and vehicle |
|
| 图 6 车辆与桥面接触示意图 Fig. 6 Schematic diagram of a vehicle running on bridge deck |
以车轮与桥面接触点处不脱离为条件,联立(1)、(3)及(5)式可得时变耦合振动方程:
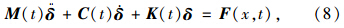
3 试验工况及测点布置 3.1 试验工况
(1)车辆与桥梁动力特性
为分析空心板桥及试验车辆动力特性,采用无障碍匀速激振和环境激振两种方法,测试桥梁和车辆振动特性。试验过程中,采用三轴自卸汽车,该车前轴与中轴间距4.2 m,中轴与后轴间距1.4 m,前轴轴重64.6 kN,中轴和后轴轴重为263.6 kN。试验测试前,车架上固定一个加速度传感器,给车辆施以初始激励,测试车辆振动响应并对其进行功率谱密度分析。使用1个高灵敏度加速度传感器,传感器布置于边梁跨中,对桥梁施加初始激励,测试桥梁振动加速度信号,并对其进行功率谱密度分析,分析桥梁结构自振频率。
(2)最不利极限承载能力布载
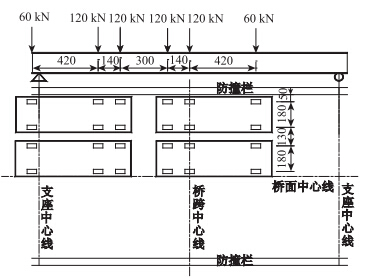
按铰接板梁法设计空心板桥,横向分布系数1号梁最大,为0.425,按照荷载等效、保证荷载效率系数大于85%小于105%,以1号梁跨中汽车荷载最大弯矩值进行荷载等效布置。极限承载力试验研究跨中截面最大正弯矩、最大竖向挠度及支点截面最大剪力3种工况,荷载布置如图 7所示。
|
| 图 7 承载能力等效荷载布置(单位:cm) Fig. 7 Layout of equivalent load bearing capacity(unit: cm) |
(3)单车静、动载试验
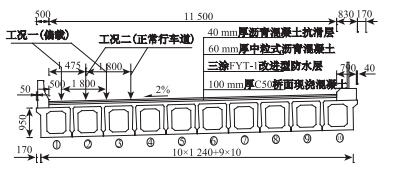
为测试车辆以不同速度、行车道位置对空心板桥各片梁的位移、应变冲击效应,车辆加载时,按图 8所示工况加载:工况一(偏载),车辆按最不利位置行驶(距路缘石0.5 m),车辆荷载作用于1、3号梁;工况二(正常行车道),车辆荷载按标准车道位置行驶,车辆荷载作用于2、3号梁。测试时,采用东华测试系统DHDAS 5 920配合电涡流位移传感器及应变测试系统,测试单车荷载按偏载及正常行车道,以10~50 km/h速度行驶时的各片梁动态位移和应变时程响应。
|
| 图 8 车辆荷载工况(单位:cm) Fig. 8 Positions of vehicle loads (unit: cm) |
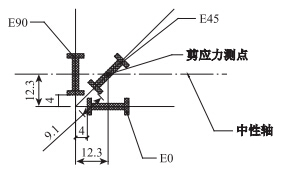
极限承载力最大正应力,在跨中弯矩控制截面布置20个应变测点,每片空心板梁底板各布置2个应变片,测点布置如图 9所示。支点截面主要测试剪应力和主拉应力,在腹板中性轴附近的面布置1组直角形应变花,直角形应变花由3个呈45°间隔分布的传感器组成。3个传感器编号分别为E0、E45、E90,腹板面应变花测点构造见图 10。

|
| 图 9 应变测点布置图 Fig. 9 Layout of strain measuring points |
|
| 图 10 应变花构造图(单位:cm) Fig. 10 Structure of strain rosette (unit: cm) |
空心板桥车桥耦合振动主要分析跨中和1/4位置的动位移和动应变响应。在1~5号梁跨中梁底及1~3号梁1/4位置各布置一个电涡流位移传感器;在1~3号梁跨中梁底各布置两个应变片,4、5号梁跨中及1~5号梁1/4位置各布置一个应变片。全桥共布置8个动位移测点,13个动应变测点。
4 试验与理论结果对比分析 4.1 空心板桥动力特性对比分析
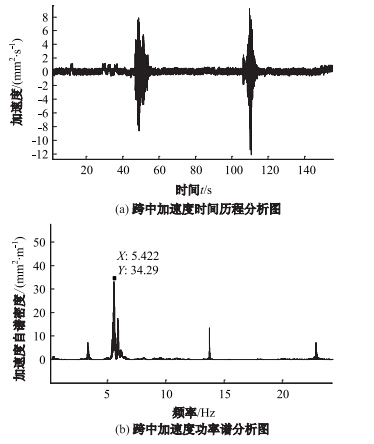
实测试验车辆的一阶频率和二阶频率分别为1.60 Hz 和2.63 Hz,本文选取车辆模型理论基频1.65 Hz,实测车辆基频与本文选取车辆模型理论基频误差为3.03%。实测空心板桥跨中自振加速度时程响应曲线及功率谱密度曲线见图 11。1为梁壳组合模型与铰接梁模型的频率及振型对比分析。从图 11和1中可以看出,实测空心板桥一阶频率为5.422 Hz,梁壳组合模型理论频率为5.116 Hz,铰接梁模型理论频率为4.876 Hz,梁壳组合模型和铰接梁模型的一阶频率接近,均为竖向正对称振型;二阶频率,实测值为13.293 Hz,梁壳组合模型为11.864 Hz,铰接梁模型为9.872 Hz,二阶振型梁壳组合模型为竖向翘曲振型,铰接梁模型现出明显的横向翘曲振动,梁壳组合模型横向连接刚度大于铰接梁模型,梁壳组合模型二阶频率大于铰接梁模型二阶频率;随着频率阶数增加,铰接梁模型横向扭转效应较梁壳组合模型明显。实测一、二阶频率均大于理论频率,空心板梁桥实际刚度大于理论刚度。
|
| 图 11 跨中加速度振动响应分析图 Fig. 11 Analysis diagram of mid-span accelerate vibration response |
| 频率阶数 | 梁壳组合模型 | 铰接梁模型 | 实测 | |||
| 频率/Hz | 振型特点 | 频率/Hz | 振型特点 | 频率/Hz | ||
| 一 | 5.116 | 竖向正对称 | 4.877 | 竖向正对称 | 5.422 | |
| 二 | 11.864 | 竖向翘曲 | 9.872 | 横向扭转翘曲 | 13.293 | |
| 三 | 19.647 | 竖向反对称 | 15.663 | 横向扭转 | — | |
| 四 | 28.324 | 竖向反对称扭转 | 18.716 | 竖向反对称 | — | |
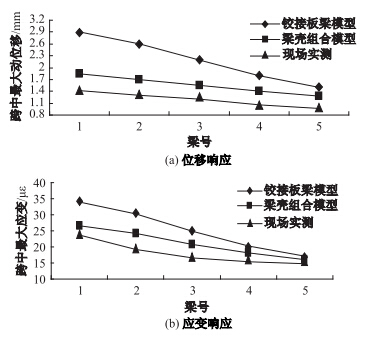
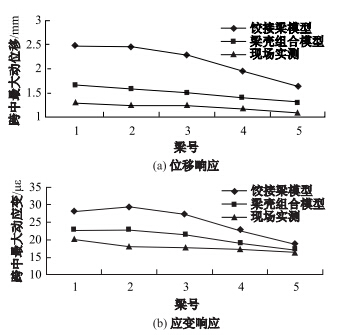
空心板桥采用铰接与刚接两种有限元模型,单车按偏载和正常行车道加载于跨中,铰接梁法、梁壳组合法及实测跨中应变、位移关系对比见图 12和图 13。从图中可以看出,现场实测及梁壳组合模型计算的1~5号梁跨中位移和应变,横向变化现出明显的线性关系;车辆按正常行车道行驶时,铰接梁法跨中静响应横向变化现明显非线性关系;梁壳组合模型计算单车荷载作用下,各片梁静态响应及横向变化规律与实测值更接近。
|
|
图 12 偏载工况各片梁跨中最大静载响应
Fig. 12 Maximum static responses of different beams at mid-span (unbalance loading) |
|
| 图 13 正常行车道工况各片梁跨中最大静载响应 Fig. 13 Maximum static responses of different beams at mid-span (normal lane) |
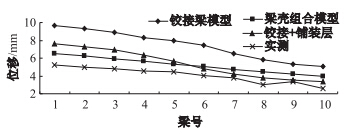
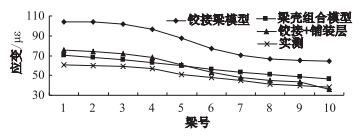
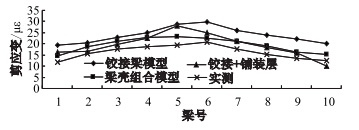
按承载能力等效加载时,空心板桥1~10号梁跨中梁底竖向位移和应变横向变化关系见图 14和图 15;图 16为支点剪应变横向变化关系图。从位移和应变横向变化可以看出,铰接梁法现出明显的非线性;考虑铺装层参与受力的铰接梁模型,位移和应变横向变化处于铰接梁模型和梁壳组合模型之间;实测位移和应变均比3种模型理论值小,但响应横向变化规律与梁壳组合模型更接近,这一结论与文献[3],[6]一致,空心板桥受载时,各片梁横向相互作用,且桥面铺装层参与受力。从支点剪应变横向变化关系可以看出,3种模型理论值与现场实测值横向变化现出明显的非线性,且5、6号梁剪应变最大,实测剪应变与梁壳组合模型更接近。
|
| 图 14 跨中最大位移变化关系图 Fig. 14 Variation of maximum displacement at mid-span |
|
| 图 15 跨中最大应变变化关系图 Fig. 15 Variation of maximum strain at mid-span |
|
| 图 16 支点最大剪应变变化关系图 Fig. 16 Variation of maximum shear strain at supporting point |
为研究空心板桥建模方法对车桥耦合振动响应的影响,2分析汽车荷载按偏载和正常行车道两种工况加载时,空心板桥分别按梁壳组合法和铰接梁法建模,跨中和1/4位置各片梁的最大静挠度和冲击系数关系对比。从中可以看出,铰接梁法车轮直接接触各片梁跨中最大静载响应明显大于梁壳组合法,各片梁跨中位移横向变化幅值大于1/4位置。从两种模型的冲击系数来看,偏载光滑路面工况下,铰接梁模型冲击系数大于梁壳组合模型冲击系数,车辆按正常行车道行驶时,两者冲击系数相差不大,车轮直接接触的空心板冲击系数,铰接梁模型略小于梁壳组合模型;考虑桥面不平顺的影响,B级路面工况下,铰接梁模型的偏载跨中位移冲击系数明显大于梁壳组合模型;正常行车道工况下两者冲击系数相差不大,铰接梁模型冲击系数略大于梁壳组合模型;车辆按偏载和正常行车道行驶时,铰接梁模型1/4位置的冲击系数均大于梁壳组合模型冲击系数,且铰接梁模型冲击系数横向变化幅度大于梁壳组合模型冲击系数。
| 响应位置 | 力学指标 | 荷载工况 | 梁壳组合模型 | 铰接梁模型 | ||||||||
| 1号梁 | 2号梁 | 3号梁 | 4号梁 | 5号梁 | 1号梁 | 2号梁 | 3号梁 | 4号梁 | 5号梁 | |||
| 跨中位置 |
最大静挠度 /mm | 偏载 | 2.038 5 | 1.879 5 | 1.718 7 | 1.564 4 | 1.421 5 | 3.438 | 3.141 | 2.677 2 | 2.234 3 | 1.915 7 |
| 正常行车道 | 1.858 7 | 1.767 3 | 1.665 2 | 1.552 6 | 1.439 4 | 3.297 | 3.302 | 3.075 | 2.667 | 2.262 1 | ||
|
冲击系数μ (光滑) | 偏载 | 0.056 6 | 0.066 6 | 0.078 3 | 0.087 8 | 0.097 6 | 0.092 9 | 0.138 6 | 0.221 5 | 0.292 9 | 0.311 3 | |
| 正常行车道 | 0.083 6 | 0.078 6 | 0.078 5 | 0.083 9 | 0.090 8 | 0.025 7 | 0.037 7 | 0.058 7 | 0.067 5 | 0.082 0 | ||
|
冲击系数μ (B级) | 偏载 | 0.106 0 | 0.114 9 | 0.125 3 | 0.131 8 | 0.132 4 | 0.132 7 | 0.129 3 | 0.237 7 | 0.342 5 | 0.339 2 | |
| 正常行车道 | 0.083 6 | 0.078 6 | 0.078 5 | 0.083 9 | 0.090 8 | 0.101 5 | 0.055 4 | 0.099 4 | 0.140 9 | 0.140 0 | ||
| 1/4位置 |
最大静挠度 /mm | 偏载 | 1.369 3 | 1.272 4 | 1.175 4 | 1.081 4 | 0.992 3 | 2.103 2 | 1.905 2 | 1.598 9 | 1.313 5 | 1.117 2 |
| 正常行车道 | 1.293 4 | 1.201 5 | 1.136 5 | 1.068 1 | 0.995 1 | 1.786 2 | 1.799 3 | 1.670 0 | 1.430 0 | 1.195 6 | ||
|
冲击系数μ (光滑) | 偏载 | 0.138 0 | 0.136 9 | 0.134 7 | 0.134 4 | 0.140 1 | 0.313 9 | 0.391 1 | 0.537 1 | 0.664 4 | 0.737 1 | |
| 正常行车道 | 0.086 9 | 0.117 5 | 0.125 1 | 0.136 5 | 0.154 5 | 0.409 0 | 0.391 4 | 0.443 9 | 0.481 8 | 0.532 2 | ||
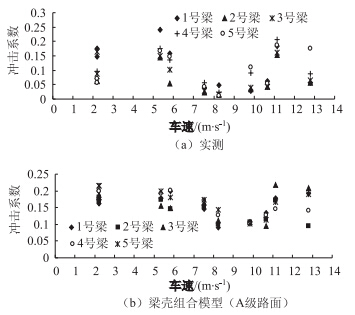
图 17为偏载工况下,现场实测和梁壳组合模型计算空心板桥1~5号梁跨中位移冲击系数离散图。从图中可以看出,实测车轮直接接触的空心板梁跨中位移冲击系数略小于A级路面模拟的冲击系数。远离车轮直接接触的空心板梁跨中位移冲击系数,实测值小于数值模拟,且实测冲击系数随速度变化离散程度大于数值模拟。实测最大冲击系数为0.241 7,最小冲击系数接近于0;理论最大冲击系数0.214 4,最小冲击系数0.090 9。实测冲击系数变化幅度范围大于理论值,这说明路面不平顺是一个非平稳随机过程,移动车辆作用于桥梁上的振动过程是一个离散的随机过程, 即使同一辆车按相同位置行驶,汽车荷载对桥梁的冲击系数也不尽相同,路面不平顺幅值大小决定桥梁振动响应的大小。同时可以看出,车轮直接接触的空心板梁冲击系数略小于非车轮直接接触空心板梁的冲击系数;实测空心板梁冲击系数和数值模拟冲击系数均能反映出车 辆随速度节拍效应,车辆以车速6 m/s和12 m/s行驶在20 m空心板梁桥时,冲击系数均有明显的增幅。
|
| 图 17 跨中位移冲击系数离散图(偏载工况) Fig. 17 Discrete diagram of displacement impact coefficient at mid-span (unbalance load) |
以20 m装配式空心板桥为背景,考虑空心板横向连接方式及桥面铺装影响,运用ANSYS建立空心板桥的梁壳组合和铰接梁两种有限元模型并与试验对比分析,可以得出以下结论:
(1)实测空心板桥一、二阶振型均为竖向振型,铰接梁模型二阶振型呈横向翘曲振动,实测空心板桥动力特性与梁壳组合模型更接近;
(2)承载能力等效荷载作用下,桥面铺装及混凝土企口缝与空心板桥共同工作,空心板桥未出现裂缝,各片梁跨中位移和应变横向变化,梁壳组合模型与实测值更接近;
(3)跨中位移冲击系数,铰接梁模型大于梁壳组合模型,实测值与梁壳组合模型更接近;横向各片梁跨中位移冲击系数变化范围,铰接梁模型明显大于梁壳组合模型;
(4)实测空心板桥静力、动力响应均与梁壳组合模型更接近,桥面铺装层与混凝土企口缝均参与受力,建议空心板桥设计时,适当考虑桥面铺装层及混凝土企口缝参与受力。
| [1] | 陈记豪,赵顺波,姚继涛.既有预应力空心板桥加宽设计的荷载横向分布计算方法[J]. 工程力学,2012,29(9):265-271.CHEN Ji-hao,ZHAO Shun-bo,YAO Ji-tao. Method for Calculating Vehicle Load Transverse Distribution in Widening Design of Existing PCHS Bridge[J]. Engineering Mechanics,2012,29(9):265-271. |
| [2] | 项贻强,邢强,邵林海,等. 铰接预应力混凝土空心板梁桥的空间受力行为及加固分析[J].东南大学学报,自然科学版,2012,42(4):734-738. XIANG Yi-qiang,XING Qiang,SHAO Lin-hai,et al. Spatial Behavior and Strengthening Analysis of Fabricated PC Hollow Slab Beam Bridge with Hinge Joints[J]. Journal of Southeast University:Natural Science Edition,2012,42(4):734-738. |
| [3] | 许国平. 空心板桥桥面铺装对主梁受力性能影响分析[J]. 公路工程,2012,7(3):111-115.XU Guo-ping. Bridge Deck Pavement on the Main Girder Performance Analysis of Hollow-slab[J]. Highway Engineering,2012,7(3):111-115. |
| [4] | 周艳清,陈志刚. 汽车荷载作用下铰接板梁桥的空间动力响应分析[J].暨南大学学报:自然科学与医学版,2012,33(3):323-328. ZHOU Yan-qing,CHEN Zhi-gang. Spatial Dynamic Response of Hinge Joint Voided Slab Bridge due to Moving Vehicles[J]. Journal of Jinan University:Natural Science & Medicine Edition,2012,33(3):323-328. |
| [5] | 王解军,张伟. 汽车荷载作用下梁桥的动力冲击效应研究[J]. 振动与冲击,2007,26(6):125-128.WANG Jie-jun,ZHANG Wei. Study of Dynamic Impact Effects of Moving Vehicle Loading on Beam Bridge[J]. Journal of Vibration and Shock,2007,26(6):125-128. |
| [6] | 唐国斌,项贻强,管品武. 桥面铺装对中小跨径桥梁力学性能影响研究[J]. 公路交通科技,2012,27(12):94-98.TANG Guo-Bin,XIANG Yi-qiang,GUAN Pin-wu. Effect of Deck Pavement on Mechanical Performance of Medium-span and Short-span Bridges[J]. Journal of Highway and Transportation Research and Development,2012:27(12):94-98. |
| [7] | 陈记豪,赵顺波,姚继涛. 装配式简支空心板桥上部结构整体性的评价[J]. 混凝土,2012,(11):113-118. CHEN Ji-hao,ZHAO Shun-bo,YAO Ji-tao. Analysing of the Integrity of the Superstructure of the Assembled Simply-supported Hollow Slab Bridge[J]. Concrete,2012,(11):113-118. |
| [8] | 张蓓,徐天昭,王复明,等. 预应力混凝土空心板梁桥承载能力实桥试验研究[J].公路,2008,(6):1-5.ZHANG Bei,XU Tian-zhao,WANG Fu-ming,et al. Experiment and Study on Bearing Capacity of Actual Prestressed Concrete Hollow Slab Beam Bridge [J]. Highway,2008,(6):1-5. |
| [9] | 贺君,雷俊卿,肖长礼. 装配式空心板混凝土桥面结构计算分析与试验研究[J]. 北京交通大学学报,2005,29(4):57-61.HE Jun,LEI Jun-qing,XIAO Chang-li. Computational Analysis and Experimental Research of Assemble Type Concrete Cellular Slab Bridge Deck[J]. Journal of Beijing Jiaotong University,2005,29(4):57-61. |
| [10] | 桂水荣,陈水生,赵辉,等. 基于LS-DYNA公路桥梁车桥耦合振动模型[J].公路交通科技,2013,30(7):40-45.GUI Shui-rong,CHEN Shui-sheng,ZHAO Hui,et al. Model of Highway Bridge Subjected to Vehicle-bridge Coupled Vibration Based on LS-DYNA[J]. Journal of Highway and Transportation Research and Development,2013,30(7):40-45. |
| [11] | 桂水荣,陈水生,唐志军. 基于Fourier逆变换法的桥面不平度模拟及测试分析[J].公路工程,2007,32(6):39-43.GUI Shui-rong,CHEN Shui-sheng,TANG Zhi-jun. Numerical Simulation Based on Fourier Inverse Transform and Analysis of Testing of Road Surface Roughness on Bridge[J]. Highway Engineering 2007,32(6):39-43. |
| [12] | HENCHI K,FAFARD M,TALBOT M, et al. An Efficient Algorithm for Dynamic Analysis of Bridges under Moving Vehicles using a Coupled Modal and Physical Components Approach[J]. |
| [13] | 王运金,桂水荣,陈水生.连续梁桥车桥耦合振动分析的数值解法[J]. 华东交通大学学报,2007,24(4):25-29.WANG Yun-jin,GUI Shui-rong,CHEN Shui-sheng. An Efficient Algorithm for Coupled Vibration Analysis of Continuous Bridges under Moving Vehicle[J]. Journal of East China Jiaotong University,2007,24(4):25-29.. |
 2014, Vol. 31
2014, Vol. 31

 ,
,