扩展功能
文章信息
- 张东, 黄晓明, 田飞
- ZHANG Dong, HUANG Xiao-ming, TIAN Fei
- 级配碎石动三轴试验离散元模拟
- Simulation of Dynamic Triaxial Test of Graded Crushed Stone by Discrete Element Method
- 公路交通科技, 2014, Vol. 31 (12): 39-42,49
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (12): 39-42,49
- 10.3969/j.issn.1002-0268.2014.12.007
-
文章历史
- 收稿日期:2013-09-10
2. 东南大学 交通学院, 江苏 南京 210096
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
级配碎石是一种常见的筑路材料,广泛用于道路底基层以及沥青面层和半刚性基层之间。在荷载作用下,级配碎石的力学响应依赖于加载历史,在荷载作用后会有残余的塑性变形。基于此,研究人员提出了回弹模量来表征级配碎石的这种特性。设级配碎石试件承受的偏应力为σd,加载后的回弹应变为ε1,则在这样的应力状态下级配碎石的回弹模量可由式(1)计算。

岩土工程行业最先引入三轴试验岩土力学问题,并通过实践证明了这个试验的有效性。道路工作者把三轴试验原理引入公路工程中并对其进行了一定的改进,通过研究证明重复加载的动三轴试验能够取得更好的效果,利用动三轴试验可以测定级配碎石的回弹模量。在级配碎石动三轴试验中,首先对级配碎石试样施加恒定的侧向围压,然后对试样施加正弦波动荷载。研究发现[1],采用周期为1.0 s 的正弦波荷载最接近级配碎石在实际道路中所承受的应力状况,其中,加载时间为0.1 s,卸载时间为0.9 s。但是,动三轴试验需要依赖昂贵精密的仪器设备。利用数值方法模拟级配碎石的动三轴试验可以极大地节省科研成本和时间。
1 离散元方法的基本原理
Cundall在1971年提出了离散元方法,用于分析岩石力学问题[2],并在之后将离散元方法运用于岩土材料的研究[3]。自从商用离散元软件PFC (Particle Flow Code)[4, 5]推出以来,离散元方法被广泛用于分析颗粒材料体系和以颗粒材料为主的复合材料的力学行为[6, 7, 8, 9]。在离散元模拟中,颗粒间相互独立,只在接触点处相互作用。颗粒间的受力和运动遵从牛顿第二定律。在离散元软件PFC中,使用力-位移方程和运动方程描述颗粒的受力和运动:力-位移方程描述了颗粒间接触处的相对位移和作用在颗粒上的接触力之间的关系;运动方程描述了单个颗粒的平动和转动。采用计算时步算法(timestepping algorithm),在每个颗粒上反复使用运动方程,在颗粒间的接触处反复使用力-位移方程,并持续更新墙体的位置。计算循环如图 1所示。在每个时间步开始时,更新颗粒之间和颗粒与墙体之间的接触,使用力-位移方程更新接触力;然后,使用运动方程更新颗粒的速度和位置,同时根据指定的墙体速度,更新墙体的位置。

|
| 图 1 PFC中的计算循环 Fig. 1 Calculation cycle in PFC |
本文使用二维离散元软件PFC2D模拟级配碎石的动三轴试验。按照下述方法生成级配碎石离散元试件:
(1) 指定试件的高度、宽度、初始孔隙率以及颗粒的最大和最小半径,并在给定初始信息的基础上计算需要生成的各种粒径碎石的颗粒数量。
(2) 按照给定的缩放比例控制系数mult缩小每个颗粒的半径,在试件范围内按照缩小后的半径生成基本颗粒,颗粒生成后再将颗粒半径扩大mult倍。
(3) 给颗粒赋予一定的刚度,使用CYCLE命令运行程序,消除颗粒间的重叠。
级配碎石在最佳含水量时成型。在含水状态时,粒径为0.075~1.18 mm的细颗粒起到一定的黏结作用,并且小于1.18 mm的颗粒数目巨大,在模拟时无法全部生成。基于此,本文将粒径小于1.18 mm的碎石颗粒简化为黏结力来等效替代。此外,本文假定各档碎石的质量比近似等于二维离散元试件中对应尺寸圆盘的面积比。这和实际情形在一定程度上有所差别。图 2是生成的级配碎石离散元试件。

|
| 图 2 级配碎石离散元试件 Fig. 2 Discrete element sample of graded crushed stone |
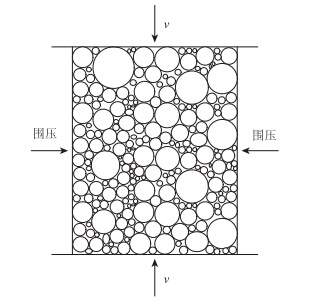
如图 3所示,在模拟级配碎石动三轴试验时,在级配碎石试件两端和两侧生成墙体。两端的墙体用于模拟加载压头,侧面的墙体用于模拟围压。在试验过程中,两端的墙体通过指定的速度向试样施加荷载,侧面墙体通过不断调整径向速度对试样施加恒定的围压。侧面墙体的径向速度使用一种数值伺服机制(numerical servo-mechanism)自动控制。这种伺服机制采用下述算法[4, 5, 10]。
|
| 图 3 虚拟动三轴试验示意图 Fig. 3 Schematic diagram of virtual dynamic triaxial test |
墙体的速度方程为:
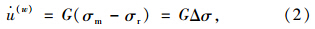
在一个时间步中,由于墙体运动引起的墙体上力的最大增量为:
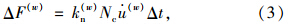
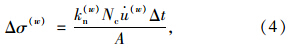
为了保证计算的稳定性,墙体上应力变化的绝对值必须小于墙体设定应力和实际应力的差的绝对值。在实际程序中,使用安全系数α来确保计算的稳定性:
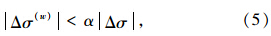
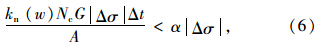
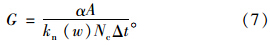
由于级配碎石动三轴试验需要施加轴向正弦波荷载,该正弦波荷载周期为1 s,其中加载时间为0.1 s,卸载时间为0.9 s。为了模拟正弦波荷载,本文通过PFC2D中的FISH语言编写了用户子程序。其中,加载卸载的控制是通过设置控制变量con_time来实现的。当con_time小于0.1 s时对试件进行加载;当con_time大于0.1 s时对试件进行卸载。需要注意的是,轴向正弦波荷载的施加也是通过上述伺服控制机制来实现的。通过伺服控制机制将需要施加的轴向正弦波荷载转化为速度施加到墙体上,实时对比应力误差并调整墙体速度。
4 离散元模型微观参数的计算和校正
根据级配碎石中颗粒之间的接触性质,本文选择线性刚度模型、滑动模型和点连接模型来模拟颗粒之间的相互作用。线性刚度模型可以模拟碎石的刚度特性,滑动模型可以模拟碎石之间的相对运动和摩擦,而点连接模型可以模拟粒径小于1.18 mm的矿料在试件中的黏结作用。
与线性刚度模型、滑动模型和点连接模型对应的微观参数分别是颗粒的法向刚度Kn和切向刚度Ks、颗粒间的摩擦系数μ以及法向连接强度n_bond和切向连接强度s_bond。离散元微观参数一般无法直接获得,通常利用微观参数与宏观参数之间的关系计算得到。但通过这种方式得到的微观参数一般需要经过校正才能用于离散元模拟。校正方法是:(1)首先利用计算得到的微观参数模拟室内试验,然后将模拟结果同室内试验结果进行对比。(2) 如果两组结果大致吻合,则可以使用这组微观参数;否则,调整微观参数的取值,重新模拟,直到两组结果吻合为止。
参考文献[5, 11, 12],可以利用式(8)、(9)计算碎石颗粒的法向刚度和切向刚度:
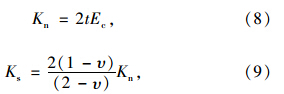
通过模拟级配碎石动三轴试验的一组试验结果,经过反复调整,本文最后得到的一组微观参数如表 1所示。
| 参数名称 | 参数值 |
| 颗粒密度 /(kg·m-3) | 2.6×103 |
| 接触杨氏模量Ec /GPa | 0.5 |
| 切向刚度Ks /Pa | 1×1010 |
| 法向刚度Kn /Pa | 1.05×1011 |
| 摩擦系数μ | 0.5 |
| 切向连接强度s_bond/N | 6.7×102 |
| 法向连接强度n_bond/N | 7.4×102 |
5.1 级配碎石回弹模量测试
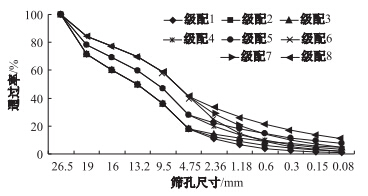
选取8组级配碎石,进行室内回弹模量测试,这8种级配碎石的级配如图 4所示。级配碎石为轧制石灰岩。为了减小脱模对级配碎石试件的影响,采用对开的模具成型试件,如图 5所示。按照最佳含水量加水,并拌和均匀,在模具内套一层乳胶套,然后将级配碎石分5次倒入模具击实。级配碎石试件的直径为100 mm,高度为200 mm。动三轴试验设备为澳大利亚IPC公司生产的综合测试仪UTM-25。试验时,围压为20.7 kPa,竖向重复正弦波荷载的幅度为50.8 kPa。正弦波荷载的周期为1 s,其中加载时间为0.1 s,卸载时间为0.9 s。回弹模量测试结果如图 6所示。
|
| 图 4 八种级配碎石的级配 Fig. 4 Gradations of 8 types of graded crushed stone |

|
| 图 5 对开模具 Fig. 5 Folio mould |
|
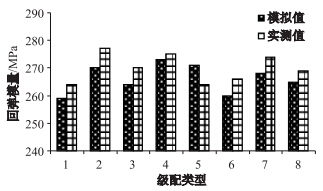
| 图 6 回弹模量模拟结果和实测结果 Fig. 6 Simulation result and laboratory test result of resilience modulus |
按照图 4中的8组级配,使用本文所述方法建立级配碎石离散元模型,模拟级配碎石的动三轴试验,并根据模拟结果计算回弹模量。图 6是这8组级配碎石回弹模量的离散元模拟结果和实测结果。由图 6可知,利用离散元模拟得到的回弹模量和实测结果非常吻合,误差都在3%以内。此外,除了第5组级配碎石,其余级配碎石的回弹模量的离散元模拟结果都比实测结果小。这主要是由两种原因造成的:第一是因为本文使用了二维离散元方法,在二维离散元模拟中,碎石颗粒被简化成平面圆盘,减少了颗粒间的接触点数目,从而使回弹模量有所减少;第二是因为本文将碎石颗粒直接简化为圆盘,没有考虑碎石颗粒的不规则形状和棱角性,从而也在一定程度上影响了模拟精度。 6 结论
本文使用离散元方法模拟了级配碎石的动三轴试验,提出了级配碎石离散元试件的生成方法、虚拟围压和正弦波动荷载的实现方法以及离散元微观参数的校正方法。对比了8组级配碎石回弹模量的离散元模拟结果和实验室实测结果,比较结果表明,利用离散元模拟得到的回弹模量和实测结果非常吻合,误差都在3%以内。
| [1] | 袁峻.级配碎石基层性能与设计方法的研究[D].南京: 东南大学,2004.YUAN Jun. Study of Performance of Graded Crushed Stone Base and Design Method[D]. Nanjing: Southeast University,2004.[2] CUNDALL P A. A Computer Model for Simulating Progressive Large-scale Movements in Blocky Rock Systems[C]//Proceedings of the International Symposium on Rock Fracture. Nancy,France: International Society of Rock Mechanics,1971. |
| [3] | CUNDALL P A,STRACK O D L. A Discrete Numerical Model for Granular Assemblies [J]. |
| [4] | Itasca Consulting Group. PFC 2D [M]. Ver.3.1. Minneapolis: Itasca Consulting Group,2004. |
| [5] | Itasca Consulting Group. PFC 3D [M]. Ver.3.1. Minneapolis: Itasca Consulting Group,2004. |
| [6] | KHATTAK M J,ROUSSEL C. Micromechanical Modeling of Hot-Mix Asphalt Mixtures by Imaging and Discrete Element Methods [J]. |
| [7] | CAI W,MCDOWELL G R,AIREY G D. Discrete Element Modelling of Uniaxial Constant Strain Rate Tests on Asphalt Mixtures [J]. |
| [8] | HUANG Zhi-yi,YANG Zhong-xuan,WANG Zhen-yu. Discrete Element Modeling of Sand Behavior in a Biaxial Shear Test [J]. |
| [9] | ZHANG D,HUANG X,ZHAO Y. Algorithms for Generating Three-dimensional Aggregates and Asphalt Mixture Samples by the Discrete Element Method [J]. |
| [10] | 张东. 沥青混合料粗集料的形态特征研究和力学性能的离散元模拟 [D]. 南京: 东南大学,2013.ZHANG Dong. Simulation of Morphology of Coarse Aggregates and Its Mechanical Performance by Discrete Element Method[D]. Nanjing: Southeast University,2013. |
| [11] | LIU Y,DAI Q,YOU Z. Viscoelastic Model for Discrete Element Simulation of Asphalt Mixtures [J]. |
| [12] | 陈俊. 基于离散元方法的沥青混合料虚拟疲劳试验研究 [D]. 南京: 东南大学,2010.CHEN Jun. Virtual Fatigue Tests of Asphalt Mixture Based on Discrete Element Method[D]. Nanjing: Southeast University,2010. |
 2014, Vol. 31
2014, Vol. 31

 ,
,