扩展功能
文章信息
- 张润初, 杜倩云, 俞祝良, 刘浩, 张可
- ZHANG Run-chu, DU Qian-yun, YU Zhu-liang, LIU Hao, ZHANG Ke
- 一种利用参考图象与路面信息的道路监控摄像机标定方法
- A Calibration Method for Road Monitoring Cameras Exploiting Reference Images and Roadway Information
- 公路交通科技, 2014, Vol. 31 (11): 137-141
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (11): 137-141
- 10.3969/j.issn.1002-0268.2014.11.022
-
文章历史
- 收稿日期:2014-2-17
2. 北京市交通信息中心, 北京 100161;
3. 北京市交通运行监测调度中心, 北京 100161
2. Beijing Transportation Information Center, Beijing 100161, China;
3. Beijing Transportation Operation Coordination Center, Beijing 100161, China
近几十年来,智能交通系统(Intelligent Transpor-tation System,ITS)中基于机器视觉的研究得到了越来越多科研人员的重视[1,2]。图像识别技术在交通领域的应用也日益广泛,道路监控摄像机的标定一直是一个热门课题[3,4]。通过对道路摄像机的标定,可以构建起2-D图像平面与3-D实际场景的对应关系,从而获取到更为准确的交通参数,如车辆平均速度[5]、车辆类型[6]、路面占有率和车流量[7]等信息。
摄像机的标定从广义上可以分为:传统标定和自标定[8]。传统标定具有标定精度高的特点,但需要在场景中放置标定参照物;自标定不需要标定参照物,但需要获取同一场景不同角度的图像信息。
针对交通场景的摄像机标定,研究者们提出了各种不同的解决方法。这些方法可以归结为:(1)已知某些摄像机的参数,如摄像机的高度或者俯角等[9,10]。当摄像机的高度已知时,可以通过道路标志线的动态检测来实现摄像机参数的动态校正,但是对于高度比较难测量或者高度信息未知情况,这种方法就不适用了。(2)使用消失点[11,12]或者消失线[13] 。一般都需要附加已知的先验知识,如车道宽度、平行于车道的一条线段的实际长度、摄像机距离车道边线的最短水平距离和摄像机离地面的高度等,这些先验知识中有的是易于测量的,有的则不然,而车道的宽度则可以依据道路标准来得到;而且,当使用的消失点数目多于一个时,有可能出现其中的一个消失点趋于无穷的“病态条件”[15],这时就不能单纯通过消失点的值来计算摄像机的参数。(3)使用场景中的已知几何模型,如文献[14]使用交通标线端点构成的矩形框。该方法在测量精度和抗噪上有较好的效果,但需要找到实际场景中的矩形框,对于单车道或者双车道中缺乏两组白色虚线的情况要找到这样的矩形框是较难的,需要人工放置标志物,而且摄像机在监控的过程中,人工操作可能使得摄像机视野发生改变,因此标志物需要一直放置在场景中才能实现动态的校正。
本文研究了基于两个消失点的摄像机标定,并提出了“病态条件”下的可行解决方法。在一般情况下,只需要利用场景中两条已知宽度的车道标线以及一条垂直于车道标线的线段即可恢复出摄像机的参数,如焦距、俯角、与车道方向的水平夹角和距离地面的高度等。而当垂直于车道标线的线段在图像上与水平坐标轴平行或者趋于平行时,在这种病态条件出现的情况下,垂直方向的消失点在图像上将趋于无穷远,此时,无法直接通过获取消失点的值来计算摄像机的参数。为解决这一情况下的摄像机标定问题,本文提出在焦距保持不变的情况下,通过旋转摄像机来获取一组合适的参考图像,再通过参考图像来实现“病态条件”下的标定。
1 摄像机空间模型
摄像机标定的本质是为了确定内部和外部的摄像机参数,从而构建出图像坐标和世界坐标的对应关系。其中内参数包括焦距、主点、倾斜角和纵横比等;外参数包括旋转矩阵和转移向量[7,14],表示摄像机坐标与世界坐标之间的相对位置。与大部分文献一样,为了简化模型计算,本文作了一个合理的假设:主点与图像中心重合,成像平面与光轴垂直,内参数只有焦距是未确定的,其他量都是已经校正好的。
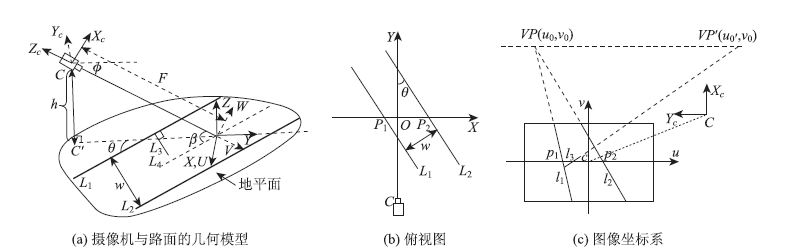
图 1(a)为摄像机与道路的几何模型,它与文献[5, 7, 16]是类似的,图 1(b)为摄像机与路面的俯视图。
|
| 图 1 摄像机与路面的坐标图 Fig. 1 Coordinate graphs of camera and road pavement |
摄像机架设在道路旁的支柱上,离地面的高度为h,俯角为Φ,与车道标志线的水平夹角为θ,光轴与道路平面交于点O,两条水平道路边线L1和L2的实际距离为w,L3垂直于L1,L4过坐标原点O并与L1平行。摄像机的坐标原点标记为点C,它在水平面的垂直投影记为点C′,CO与L4夹角为β。由图 1(a)可知,世界坐标系O-XYZ和摄像机坐标系C-XCYCZC都是服从右手定则的,其中X轴和Y轴平行于路面并且Y轴与C′O共线,Z轴垂直于路面向上。辅助坐标系O-UVW的U轴与X轴重合,坐标系绕着U轴旋转使得W轴和Z轴夹角为。摄像机坐标系的XC轴与W轴同向,YC轴和ZC轴分别与U,V轴反向,CO的实际距离记为F。
由针孔摄像机原理以及射影几何可以得到摄像机坐标与图像坐标的关系,如式(1)所示:
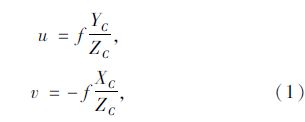
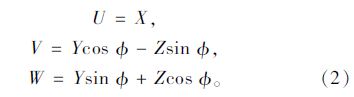
由摄像机坐标系C-XCYCZC与辅助坐标系O-UVW的平移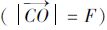 和反转关系以及式(2)可以得到摄像机坐标与世界坐标的关系,如式(3)所示:
和反转关系以及式(2)可以得到摄像机坐标与世界坐标的关系,如式(3)所示:
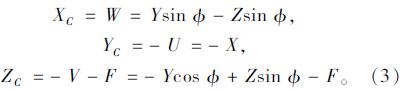
另外,由于我们研究的对象都是在路面上运动的,因此可以假设Z=0,使得模型的运算更简便。此时,将式(3)和Z=0代入(1),可以得到如下式(4):
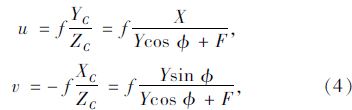
由上述公式可知,坐标平面X-O-Y与图像平面u-c-v具有一一对应的关系,因此可以通过图像坐标得到道路平面的世界坐标X,Y的值,将F=hcscΦ代入式(4)可得:
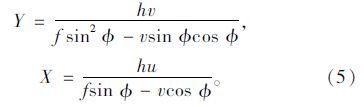
由式(5)可知,为了从图像坐标重构实际场景的坐标,需要求取h,f和值,我们引入两个消失点来求取。由文献[11, 12]可以知道,消失点指的是实际场景中的一组平行线在图像上的交点。如图 1(c)所示,l1和l2分别对应实际场景中的车道边线L1和L2,l3对应垂直于车道边线L1且与路面平行的线段L3。L1和L2在无穷远处的消失点在图像上的投影为l1和l2的交点VP(u0,v0)。由(4)可知,Y与v是一一对应的,所以一组与车道边线垂直的平行线的消失点将落在消失线v=v0上,见图 1(c)上的点VP′(u0′,v0)。
2.1 考虑θ≠0的情况令X=Ytan θ,可得:
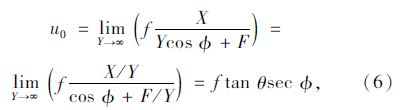
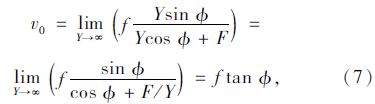
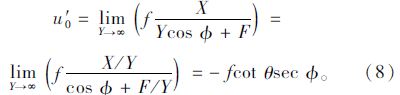
由式(6),(7),(8)这三个方程可以解出f,θ和三个未知量,如式(9)所示:
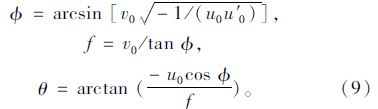
为了得到摄像机的高度h,假设车道边线L1和L2分别与OX轴交于点P1(X1,Y1,0)和P2(X2,Y2,0),图像上分别对应点p1(u1,0)和p2(u2,0)。由(4)可以得到u1和u2:
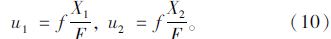
又由图 1(b)的几何关系可以得到:
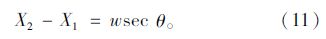
记Δu=u2-u1,则由式(10),式(11)以及h=Fsin Φ可以得到:
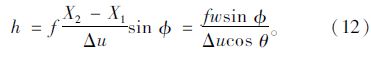
由式(8)可知,当θ=0°时,u′0趋于无穷大,此时要获取车道线垂直方向上的消失点在图像上的坐标是不可能的,因此不能直接通过消失点的值来计算摄像机的参数,而由式(6)和(8)相乘可以得到:
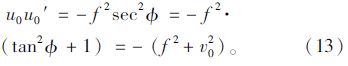
从上述公式可以看到,u0u0′是与θ无关的,且可以通过平行于车道线方向的消失点和焦距来计算得到,所以可以间接通过u0u0′的值来解式(9)中的摄像机参数。鉴于道路监控系统中广泛采用云台摄像机,可以通过远程控制来实现摄像机焦距和旋转角度的调整,因此可以在焦距保持不变的情况下,通过旋转摄像机的角度(水平偏角和俯角)来获取一组合适的参考图像,这些参考图像都是可以方便得到水平和垂直于车道方向的消失点的,然后再利用这些参考图像来得到病态条件下的摄像机参数。根据式(9)可以方便计算得到这些参考图像下的摄像机焦距,再通过均值处理,用均值作为病态条件下的焦距,从而可以计算出其他的摄像机参数。
2.3 光轴与车道线方向的夹角如图 1所示,光轴与车道线方向的夹角为β。由几何关系和三角函数变换可以得到β与Φ,θ的关系为:cos β=cosΦcos θ。所以,当θ=0°时,β=Φ;而当θ=90°时,β=90°。图 2为图 1(a)中光轴CO与L4的侧视图。

|
| 图 2 光轴与车道平行线L4的侧视图 Fig. 2 Side view of optical axis and line L4 which parallel to lane |
由图 2可以看到,摄像机观察到的一段长为l、端点在O点的线段的实际大小应为该线段在垂直于光轴方向的投影,长度为lsin β,所以,当θ由0°增大到90°时,β则由Φ增大到90°,摄像机观察到的物体的长度将会变长。此时,若通过的实际车速为V,则摄像机观察到的速度应为:VS=Vsin β,所以摄像机观察到同一速度下沿不同方向运动的物体的速度也会不同,纵向运动的物体速度最小,而横向运动的物体速度最大。
3 试验在试验前,需要找到场景中两组互相垂直的平行线,但是,由于实际场景间会存在较大差别,因此,提取的方法也有所不同。可以归结为以下两种情况:
3.1 场景中可以找到与车道线垂直的情况这种情况常见于多车道路段中有两组或以上白色虚线,可以通过相应的虚线端点来找到与车道方向垂直的线,如图 3所示。当场景中有相应的人行斑马线时,也可以利用斑马线来进行提取。此外,还有公交站路段中出现的白色虚线块也能够提取到垂直车道方向的一组平行线。

|
| 图 3 实际的交通场景 Fig. 3 Real traffic scene |
在这种情况下可以考虑人工现场标志和非人工的方式。人工现场标志可以通过放置T形架的方式来实现,将T形架的底边与车道线平行,则另一端线即为车道方向的垂直线;非人工方式可以通过提取直线的方式[12],或者通过车辆的对称性来提取,如车窗的角点、车灯、车牌和车辆的底部边缘[16]等。
本文对两幅场景(图 3 (b)和(c))进行了试验,并对场景中两条已知长度的线段进行了验证,结果如表 1所示。
| 参数 | 场景1:图 3 (b) | 场景2:图 3 (c) |
| 已知 | 车道宽度w=3.5 m; 白色虚线(图中粗线)长度l=6 m | 车道宽度w=3.35 m; 公交站白色虚线(图中粗线)长度l=5 m |
| 中间量 | 消失点的坐标: u0=-5181.3v0=3661.3u′0=8379.7Δu=1122.5 | 消失点的坐标:u0=2493 v0=2845.7u0′=-3097.1Δu=1125.7 |
| 恢复值 | 摄像机参数: f=20512.79 pixelsΦ=10.12°θ=-13.96° h=11.58 m | 摄像机参数: f=8313.5 pixelsΦ=18.90°θ=15.84°h=8.33 m |
| 测试值 | l=6.29 m,相对误差为:4.83% | l=5.22 m,相对误差为:4.4% |
由上述试验结果可以看到,该方法具有较高的精度,而且操作方便,因此,在交通场景中具有广泛的适用性。本文的校正目前采用的是人工提取标线的方法,因此存在较大的人为误差,而为了提高系统的精度和实现智能化处理,后期的研究将通过车辆的对称信息和运动光流来实现消失点的提取。
| [1] | COIFMAN B, BEYMER D, MCLAUCHLAN P, et al. A real-Time Computer Vision System for Vehicle Tracking and Traffic Surveillance[J]. |
| [2] | BUCH N, VELASTIN S A,ORWELL J. A Review of Computer Vision Techniques for the Analysis of Urban Traffic[J]. |
| [3] | MASOUD O,PAPANIKOLOPOULOS N P. Using Geometric Primitives to Calibrate Traffic Scenes[J]. |
| [4] | CATHEY F W,DAILEY D J. One-parameter Camera Calibration for Traffic Management Cameras[C] // Proceedings of the IEEE 7th International Conference on Intelligent Transportation Systems. Washington,D.C.: IEEE, 2004: 865-869. |
| [5] | SCHOEPFLIN T N, DAILEY D J. Algorithms for Calibrating Roadside Traffic Cameras and Estimating Mean Vehicle Speed[C] // Proceedings of the IEEE 10th International Conference on Intelligent Transportation Systems. Seattle, USA: IEEE, 2007: 277-283. |
| [6] | HUANG L. Roadside Camera Calibration and Its Application in Length-based Vehicle Classification[C] // 2010 2nd International Asia Conference on Informatics in Control, Automation and Robotics (CAR). Wuhan, China: IEEE, 2010: 329-332. |
| [7] | WANG K, HUANG H, LI Y, et al. Research on Lane-marking Line Based Camera Calibration[C] // 2007 IEEE International Conference on Vehicular Electronics and Safety. Beijing, China: IEEE, 2007: 1-6. |
| [8] | 邱茂林,马颂德,李毅. 计算机视觉中摄像机定标综述[J]. 自动化学报, 2000, 26(1): 43-55. QIU Mao-lin, MA Song-de, LI Yi. Overview of Camera Calibration for Computer Vision[J]. Acta Automatica Sinica, 2000, 26(1): 43-55. |
| [9] | BAS E K,CRISMAN J D. An Easy to Install Camera Calibration for Traffic Monitoring[C] // 1997 IEEE Conference on Intelligent Transportation Systems. Boston, USA: IEEE, 1997: 362-366. |
| [10] | CHAUSSE F, AUFRERE R, CHAPUIS R. Recovering the 3D Shape of a Road by On-board Monocular Vision[C] // Proceedings of the 15th International Conference on Pattern Recognition. Barcelona, Spain: IEEE, 2000: 325-328. |
| [11] | KANHERE N K, BIRCHFIELD S T. A Taxonomy and ANALYSIs of Camera Calibration Methods for Traffic Monitoring Applications[J]. |
| [12] | ZHENG Y,PENG S. A Practical Roadside Camera Calibration Method Based on Least Squares Optimization[J]. |
| [13] | WANG L L,TSAI W H. Camera Calibration by Vanishing Lines for 3-D Computer Vision[J]. |
| [14] | FUNG G S, YUNG N H,PANG G K. Camera Calibration from Road Lane Markings[J]. |
| [15] | ZHUANG H, WU W C. Camera Calibration with a Near-parallel (Ill-conditioned) Calibration Board Configuration[J]. |
| [16] | SCHOEPFLIN T N,DAILEY D J. Dynamic Camera Calibration of Roadside Traffic Management Cameras for Vehicle Speed Estimation[J]. |
 2014, Vol. 31
2014, Vol. 31
