扩展功能
文章信息
- 王晓宁, 吴志涛
- WANG Xiao-ning, WU Zhi-tao
- 低密度区高速公路平直段交通流速度和流量关系研究
- Research of Speed-volume Relationship of Expressway Straight Section in Low-density Area
- 公路交通科技, 2014, Vol. 31 (11): 130-136
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (11): 130-136
- 10.3969/j.issn.1002-0268.2014.11.021
-
文章历史
- 收稿日期:2013-10-24
基本路段交通流速度和交通量之间的关系模型是道路通行能力和服务水平划分研究的基础,能为确定单车道的基本通行能力、服务水平等级提供理论支持。而单车道通行能力和服务水平分级标准是车道数决策的关键依据,对高速公路和快速路这样建设成本高的干道尤为重要。在基本路段中,平直段(高速公路平直段是指纵坡小于3%的直线段或纵坡小于3%且半径大于1 000 m的圆曲线段)由于线形指标高,交通流速度不受线形条件约束且便于数据采集,同时视距良好开阔,车辆的行驶速度受驾驶员技术影响较小。三种优点使得平直段的速度-流量模型具有很好的代表性,其他线形处的模型可在平直段模型的基础上进行相应修正。因此,速度-流量模型是交通流理论研究中的热点问题之一,研究平直段的模型是基本路段模型的基础。从最早格林希尔治模型开始,对该模型的研究不断深入,既有成果丰硕。
格林希尔治模型是利用交通流三参数之间的数学关系,在速度和密度线性模型的基础上,推导出速度关于流量的一个二次函数。一些学者对BPR函数作数学变换后用实测数据拟合速度-流量关系模型[1,2,3],建立了速度关于流量的非整数幂函数(非分段函数)。部分学者也提出了向量自回归模型[4]。
张亚平在研究广佛高速的流量-速度关系时,指出速度和流量之间是分段的二次曲线关系[5],常成利在高速公路通行能力研究中也得出相同的结论[6]。Tracz Marian等人分析了各种条件对速度-流量模型的影响,在对比分析既有模型基础上得到了模型对其他道路交通流拟合效果差的结论[7]。美国交通工程人员根据高速公路速度-流量散点图,提出流量从零增大到实际通行能力的过程中,速度随流量的增大而线性减小;从实际通行能力减小到零的过程,速度是流量的二次函数的观点[8]。英国道路研究实验室针对高速公路提出的模型是流量从零增大到一定流量之前,速度为常数(自由流),之后随着流量的增加,速度线性减小[9]。德国交通部门进行的研究表明高速公路流量从零增大到实际通行能力的过程中,速度和流量的关系是变斜率的线性关系,不是单一斜率的线性关系,随着流量的增大,速度呈分段式线性减小趋势[8]。我国《公路通行能力手册》推荐的高速公路速度和流量关系模型为在稳定流状态下,速度是流量的二次函数;在非稳定流状态下,交通流处于紊乱状态,流量和速度之间没有必然的关系,无法用数学模型表达。
从既有研究成果来看,高速公路交通流速度和流量之间的关系模型研究逐渐向分段的函数发展。大部分研究在流量从实际通行能力减小至零(高密度、拥挤流,非稳定流状态)过程中,得到相同的结论,即速度是流量的二次函数。在流量从零增大至实际通行能力(低密度、稳定流)过程中,则出现了两种不同观点:一种认为速度随流量的增大而线性减小,另一种认为速度随着流量的增大呈二次曲线减小趋势。因此,分析低密度区速度-流量的关系模型形式具有必要性。
由于速度-流量关系模型是利用回归分析法对大量实测数据进行拟合得到的,所以存在回归模型可移植性不佳的普遍问题,这在既有研究中可以看到(各模型参数大小差异明显),利用一条高速公路的实测数据建立的模型对另一条高速公路的数据拟合效果较差。因此,为分析不同高速公路速度-流量模型的具体差异性,需选取具有代表性的不同类型高速公路平直段作为研究对象。
基于此,本文拟选取不同类型的高速公路平直段上的交通流进行研究。采集速度和流量数据后,利用统计分析手段分别建立不同类型高速公路平直段上的速度-流量模型,以研究低密度区模型具体形式,并根据不同类型高速公路平直段的模型形式和参数大小,分析高速公路类型对模型的影响。
1 速度调查和数据处理 1.1 调查地点选择及取样条件高速公路根据设计速度、所处自然地理条件、路面类型、车道数等差异可分为很多种类型。为简化研究,本文以所处自然地理条件差异为分类标准,将高速公路分为平原区高速、山岭重丘区高速和山岭微丘区高速三种类型,同时控制其他条件尽量一致,包括路面类型和车道数。平直段交通流特性不受设计速度影响,增大了目标高速公路的选取面。
经过对比分析,选取了广东省三条高速作为典型代表,分别为开阳高速(平原区高速)、京珠高速粤北段(简称京珠北高速,山岭重丘区高速)和粤赣高速(山岭微丘区高速)。三条高速公路均为双向四车道,沥青混凝土路面且路面平整度高,无影响交通流速度的破损现象,设计速度分别为120,100 km/h和100 km/h。通过查阅三条高速公路的施工图文件,在开阳高速K3197+900、京珠北高速K1933+180、粤赣高速K101+000处有上跨人行天桥,且这些桩号处于平直段,既符合研究需要,又便于数据采集。开阳高速在该段为半径是5 200 m的圆曲线,纵坡为1.5%;京珠北高速在该段为直线段,纵坡为0.3%;粤赣高速在该段为半径是4 500 m的圆曲线,纵坡为2.0%。三条高速调查断面如图 1所示。

|
| 图 1 三条高速公路调查断面照片 Fig. 1 Photos of survey sections of 3 expressways |
研究人员于2012年8月21日至25日分别在上述三个断面取样,在人行天桥上架设摄像机录制视频,连续录制时间为9:00—16:00。取样时天气晴朗,视距良好,天气状况对驾驶员的正常驾驶行为不产生影响。录制的交通流为低密度下的常态交通流,可用于后续数据提取。
1.2 统计间隔确定速度调查外业采用摄像机录制视频的方法,内业提取数据时利用premiere软件编辑录制的视频,使视频逐帧播放。提取每条车道上每辆车通过调查断面的点速度及前后相邻两辆车的车头时距,同时提取同方向两条车道上的数据。具体实施如下:在软件中为视频画面设定两个断面,以车行道分界线(高速公路车行道分界线为虚线,每段实线长度为6 m,实线间长度为9 m)长度为依据计算出两个断面间距离,根据车辆通过两个断面的时间差计算出车辆在两断面之间的平均速度,并以此平均速度作为调查断面的点速度;同车道上相邻两辆车到达指定断面的时间差即为车头时距。
建立速度-流量关系模型前,先要确定交通流参数的统计间隔。若统计间隔选取过大,会使调查时间长、工作量大;若统计间隔选取过小,会出现在一个统计间隔内的交通量仅有1辆或为0的情况,提取的数据拟合效果差,回归模型精度低。交通流参数常用的统计间隔是15 min,HCM手册推荐的最小间隔为5 min,国内关于速度-流量模型研究的文献也有以20 s,1 min,3 min,10 min作为统计间隔的。考虑到在一定范围内采用的统计间隔越短,得出的流率取值区间越大,扩大了样本的取值范围,更有利于速度-流量关系模型的建立。若无限制地缩小统计间隔,则会使流率取值范围减小,流率值变得更加集中,不利于速度-流量关系模型建立。
本次速度调查采用摄像法,可反复播放视频提取样本,时间充裕,为增大样本量,采用20 s作为统计间隔。
1.3 数据分析处理因为来车的组成状况是变化的,而速度-流量关系模型中的参数v和q却是指交通流中仅有标准小汽车时的交通流参数,所以数据处理时需要将其他车型车辆折算为标准小汽车,其他车型车辆的速度也需做相应处理。车辆的折算系数(PCE)采用《公路通行能力手册》推荐的基本路段折算系数,小型车为1.0,中型车为1.5,大型车为2.0,特大型车为3.0。速度调查时注意到,高速公路在一段比较短的时间内,通过某断面的所有车辆可以看作一个车辆组团,同时近似认为组团内的车辆都是以该组团内小型车的速度通过调查断面的。车辆组团的行驶速度采用组团内所有小型车的平均速度。若无小型车,则此样本记为无效样本,予以舍弃。
双向四车道高速公路单方向行车道的功能是靠近路肩的车道作为行车道,靠近中间带的车道作为超车道,大型车不能长时间占用超车道行驶。这种交通组织方式会使不同车道上的交通流特性不同。以开阳高速行车道和超车道上的大型车速度为例,对每条车道的大型车速度作K-S检验,检验结果如表 1所示,对应概率均大于0.05,表明在95%置信水平下两车道上大型车速度均服从正态分布。然后利用PASW软件作方差分析,结果如表 2所示。
| 单样本 Kolmogorov-Smirnov 检验 | |||
| 行车道大型车速度 | 超车道大型车速度 | ||
| N(样本量) | 201 | 202 | |
| 正态参数a,b | 均值 | 98.940 9 | 114.378 5 |
| 标准差 | 16.489 4 | 8.741 9 | |
| 最极端差别 | 绝对值 | 0.072 | 0.101 |
| 正 | 0.065 | 0.055 | |
| 负 | -0.072 | -0.101 | |
| Kolmogorov-Smirnov Z | 0.908 | 0.633 | |
| 渐近显著性(双侧) | 0.382 | 0.528 | |
| 注:a. 检验分布为正态分布;b. 根据数据计算得到。 | |||
| 车道名 | 样本量N | 速度均值 | 速度标准差 | 均值标准误 | ||
| 大型车速度 | 行车道 | 201 | 98.94 | 16.49 | 1.16 | |
| 超车道 | 202 | 114.38 | 8.74 | 0.62 | ||
| 方差方程Levene检验 | 均值方程的t检验 | |||||
| F | Sig | t | df | Sig(双侧) | ||
| 速度 | 假设方差相等 | 95.35 | 0.000 | -11.750 | 401 | 0.000 |
| 假设方差不等 | -11.733 | 303 | 0.000 | |||
从检验结果表 2知,行车道和超车道上的大型车速度方差不相等,对应的t统计量概率小于0.05,说明了在95%的置信水平下两车道的大型车速度均值存在显著性差异。同理,对开阳高速不同车道上的其他车型车辆速度和京珠北高速、粤赣高速不同车道上相同车型车辆速度进行方差分析,结果如表 3所示(3条高速公路不同车道上的每种车型车辆速度都通过K-S检验,均服从正态分布)。
| 车型 | 内容 | 开阳高速 K3197+900 | 京珠北高速 K1933+180 | 粤赣高速 K101+000 |
| 小型车 | 方差差异性 | 相等 | 不相等 | 不相等 |
| 速度均值差异性 | 无差异 | 有差异 | 有差异 | |
| 中型车 | 方差差异性 | 相等 | 不相等 | 相等 |
| 速度均值差异性 | 有差异 | 有差异 | 有差异 | |
| 大型车 | 方差差异性 | 不相等 | 相等 | 不相等 |
| 速度均值差异性 | 有差异 | 有差异 | 有差异 | |
| 特大型车 | 方差差异性 | 相等 | 相等 | 相等 |
| 速度均值差异性 | 有差异 | 有差异 | 无差异 |
表 3说明了3条高速公路不同车道上同种车型车辆速度均值大部分存在显著性差异,只有开阳高速的小型车和粤赣高速的特大型车速度均值不存在车道差异性,从侧面表明不同车道上的交通流特性不同。因此,行车道和超车道上的交通流特性存在显著性差异,速度-流量关系模型应分车道建立,即不能用同一模型表征两车道上的速度-流量关系。
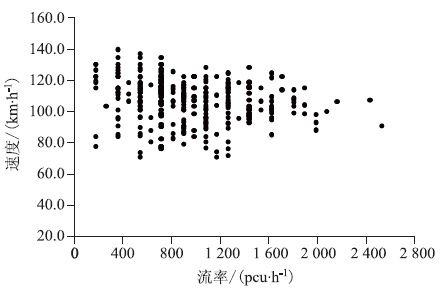
2 速度和流量关系模型建立 2.1开阳高速依据20 s的统计间隔提取速度和流量数据,统计得到行车道上速度-流量有效样本300个,超车道312个。在把20 s流量转化为小时流率后,将这些点标定在横坐标为小时流率(pcu/h)、纵坐标为速度(km/h)的坐标系上,得到数据散点图 2和图 3。
|
| 图 2 开阳高速行车道速度-流率散点图 Fig. 2 Scattergram of relation between speed and flow rate of lanes of Kaiping-Yangjiang expressway |
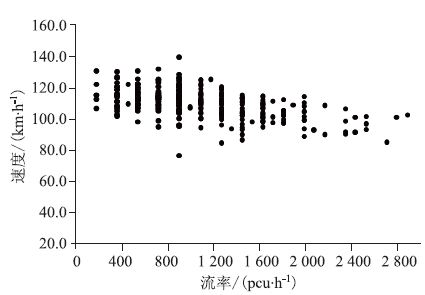
|
| 图 3 开阳高速超车道速度-流率散点图 Fig. 3 Scattergram of relation between speed and flow rate of overtaking lanes of Kaiping-Yangjiang expressway |
从图 2和图 3可以看出:
(1)行车道流率从0增大到600 pcu/h的过程中,速度的变化区间逐渐增大,且流率越小,速度的取值区间越小;流率从600增大到1 600 pcu/h的过程中速度的变化区间逐渐减小,且流率越小,速度的取值区间越大。这是因为流率很小时,车辆行驶的任意性很高,车辆速度完全取决于驾驶员的习惯及车辆性能。随着流率逐渐增大,车辆之间的干扰程度开始增大,此时仍未达到影响驾驶员习惯驾驶速度的程度,然而跟驰现象时有发生,超车现象出现频率增加,速度离散程度增大。随着流率进一步增大到实际通行能力附近,车流形成稳定流,超车变得很困难,车辆间的行驶速度和步调逐渐趋于一致。
(2)行车道车流从0增大到实际通行能力的过程中,速度取值区间中点一直在110 km/h上下浮动。
(3)超车道流率从0增大到900 pcu/h的过程中,速度的变化区间逐渐增大,且流率越小,速度的取值区间越小;流率从900增大到2 000 pcu/h的过程中速度的变化区间逐渐减小,且流率越小,速度的取值区间越大。比起行车道,超车道车辆速度取值区间长度变化程度相对较小。随着流率的增大,两车道车辆速度取值域的最大值均在变小。
(4)超车道流率从0增大到实际通行能力的过程中,速度取值区间中点从120 km/h逐渐减小为100 km/h。
(5)图 2和图 3中均出现小时流率大于车道基本通行能力的点,这是因为取20 s作统计间隔会出现瞬间某些大流率的车辆组团以较高速度通过调查断面的现象(该车辆组团与前一车辆组团无跟驰现象)。当把20 s流量放大时,流率会出现大于车道基本通行能力的现象。
(6)由于调查断面处交通流状态一直是自由流或稳定流,所以散点图中没有非稳定流的点。
经过上述分析可知,开阳高速车辆速度均值从交通量为0增大到实际通行能力的过程中一直能保持较高的水平,速度随流量的增加近似呈线性减小趋势。因此,用一次函数拟合速度和流量关系模型。利用统计软件Eviews,方法为加权最小二乘法(WLS),结果如表 4所示。
| 车道名称 | 速度-流量关系表达式 | 备 注 |
| 行车道 | v1=-0.005 835q1+112.545 8 (R2=0.91) | v1为行车道速度q1为行车道流量 |
| 超车道 | v2=-0.009 108q2+120.171 4(R2=0.97) | v2为超车道速度q2为超车道流量 |
从表达式可以看出,行车道的自由流速度为113 km/h,小于开阳高速的设计速度(120 km/h);超车道自由流速度为120 km/h,大于行车道的自由流速度,与设计速度相等。
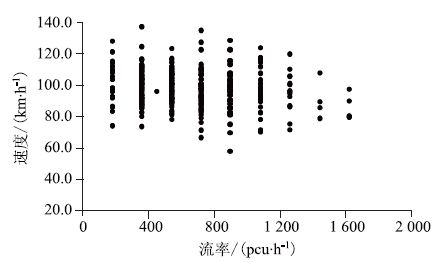
2.2 京珠北高速 统计得到行车道上速度-流率有效样本280个,超车道355个。作数据散点图 4和图 5。
|
| 图 4 京珠北高速行车道速度-流率散点图 Fig. 4 Scattergram of relation between speed and flow rate of lanes of Beijing-Zhuhai north expressway |
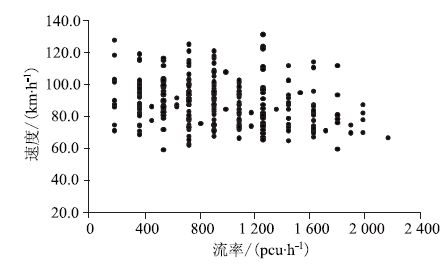
|
| 图 5 京珠北高速超车道速度-流率散点图 Fig. 5 Scattergram of relation between speed and flow rate of overtaking lanes of Beijing-Zhuhai north expressway |
从图 4和图 5可以看出:
(1)行车道流率在200 pcu/h左右时,车辆的行驶速度取值区间非常大,但以过大或过小速度行驶的车辆数量占总车辆数的比例很小。若舍弃这些速度偏离过大的点,则可以得到和开阳高速一样的趋势,即速度的取值区间长度先随着流率的增大而逐渐增大,之后又随流率的增大而逐步减小。这个极值点在600~800 pcu/h之间。
(2)超车道速度取值的离散程度较行车道小,随着流率的逐渐增大,速度取值区间长度先逐渐增大,后逐渐减小,极值点在800~1 000 pcu/h之间。
(3)流率从0增大到实际通行能力的过程中,行车道和超车道车辆速度取值在很长一段区间内可以保持自由流水平,仅在接近实际通行能力的一小段区间出现较快的减小。
经分析可知,京珠高速粤北段上车辆速度在交通量从0增大到实际通行能力的过程中能一直保持较高的速度,速度随着流量的增大而减小趋势很慢。与开阳高速的方法一样,用一次函数拟合速度-流量模型,结果如表 5所示。
| 车道名称 | 速度-流量关系表达式 | 备 注 |
| 行车道 | v1=-0.008 068q1+96.135 1(R2=0.84) | v1为行车道速度q1为行车道流量 |
| 超车道 | v2=-0.007 462q2+103.942 7(R2=0.89) | v2为超车道速度q2为超车道流量 |
从表达式可以看出,行车道的自由流速度为96 km/h,小于京珠北高速的设计速度(100 km/h);超车道自由流速度为104 km/h,大于行车道的自由流速度,稍大于设计速度。
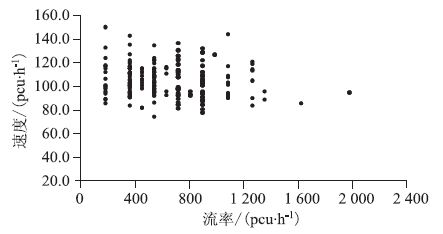
2.3 粤赣高速统计得到行车道上速度-流量有效样本203个,超车道245个。作数据散点图 6和图 7。
|
| 图 6 粤赣高速行车道速度-流率散点图 Fig. 6 Scattergram of relation between speed and flow rate of lanes of Guangdong-Jiangxi expressway |
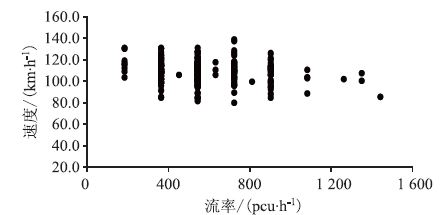
|
| 图 7 粤赣高速超车道速度-流率散点图 Fig. 7 Scattergram of relation between speed and flow rate of overtaking lanes of Guangdong-Jiangxi expressway |
从图 6和图 7可以看出:
(1)行车道在低流率状况下(小于200 pcu/h)的速度离散程度最大,但速度值过大或过小的点数量很少。若舍弃偏离较大的点,速度取值区间的长度先随流率增大而增大,后随流率的继续增大而减小,极值点在600~800 pcu/h之间。
(2)相同流率下,超车道车辆速度取值范围较行车道集中,速度取值区间的长度先随流率增大而增大,后随流率的继续增大而减小,极值点在800~1 000 pcu/h之间。
(3)在采集到的流率范围内,车辆在行车道和超车道上的速度都能保持在较高水平。经分析可知,粤赣高速上车辆速度在交通量从0增大到实际通行能力的过程中一直能保持较高的车速,速度随流率的增加而减小趋势很慢。与开阳高速的方法一样,用一次函数拟合速度-流量模型,结果如表 6所示。
| 车道名称 | 速度-流量关系表达式 | 备注 |
| 行车道 | v1=-0.005 980q1+109.231 8(R2=0.91) | v1为行车道速度q1为行车道流量 |
| 超车道 | v2=-0.008 465q2+114.023 7(R2=0.93) | v2为超车道速度q2为超车道流量 |
从表达式可以看出,行车道的自由流速度为109 km/h,大于粤赣高速的设计速度(100 km/h);超车道自由流速度为114 km/h,大于行车道的自由流速度。自由流速度比设计速度大的现象说明了低设计速度的高速公路在某一段的线形指标可能和高设计速度高速公路的相同。
3 综合分析综合对开阳高速、京珠北高速、粤赣高速这三条典型高速公路速度-流量关系的分析,低密度区高速公路平直段速度-流量之间的关系有如下特点:
(1)三条高速公路低密度区速度-流量关系均表现出速度随流量增大呈缓慢减小(斜率很小)的趋势,说明该趋势与高速公路类型(平原区高速、山区重丘高速、山岭微丘区)无关。速度-流量线性关系模型拟合优度R2均较大,拟合优度较好,回归通过显著性检验,说明了低密度区不同高速公路速度-流量关系可用线性模型表达,即低密度区高速公路速度-流量关系模型形式为线性模型。
(2)三条高速公路行车道和超车道上速度-流量关系模型形式虽然一致,但模型参数不相同,说明了同一高速公路不同车道上速度-流量关系模型不同,不同高速公路相同车道速度-流量关系模型也不同。不同类型高速公路速度-流量关系模型不同。
(3)超车道速度减小的斜率值呈现按平原区高速、山岭微丘区高速和山岭重丘区高速的顺序依次减小的规律,即增加同样的流量,平原区高速的速度减小值最大,山岭重丘区高速的速度减小值最小;行车道的规律与之相反。
(4)行车道自由流速度比超车道小。在达到单车道实际通行能力时,开阳高速交通流速度约为100 km/h;京珠北高速的约为80 km/h;粤赣高速的约为95 km/h。
(5)速度的取值区间长度随流量的增大而先增大后减小,行车道的极值点在600~800 pcu/h之间,超车道的极值点在800~1 000 pcu/h之间。
4 结论本文研究了三种典型四车道高速公路平直段低密度区的速度-流量关系,得到了不同高速公路模型均为线性模型,具体模型表达式有差异的结论。表明了不同高速公路平直段速度-流量模型不能用同一的表达式表征。对于同一高速公路平直段,不同车道上速度-流量关系模型表达式不同,表明了交通组织方式对关系有较大影响。上述结论在基本路段其他线形处以及在六车道、八车道高速公路上是否也成立有待于下一步研究。拥挤流的速度-流量关系模型形式为二次函数,其参数值是否与高速公路类型无关也需开展研究。
| [1] | 王文英,崔磊. 城市干道路段速度-流量模型及通行能力研究[J]. 交通标准化,2011(3):50-52. WANG Wen-ying, CUI Lei. Speed-flow Model and Traffic Capacity on Urban Arterial Roads[J]. Communications Standardization, 2011(3):50-52. |
| [2] | 任刚,刘晓庆,全林花. 大型车比例对城市道路机动车速度-流量模型的影响分析[J]. 土木工程学报,2010,43(2):133-137. REN Gang, LIU Xiao-qing, QUAN Lin-hua. Analysis of Heavy Vehicles Proportion upon Modeling Speed-flow Relationship on Urban Roads[J]. China Civil Engineering Journal, 2010, 43(2): 133-137. |
| [3] | 景鹏,孟祥海. 冰雪融冻期城市道路行车速度和流量及其关系模型研究[J]. 森林工程,2006,22(5):24-27. JING Peng, MENG Xiang-hai. The Development of Speed-Flow Model on Urban in the Period of the Melts Ice Snow[J]. Forest Engineering, 2006, 22(5):24-27. |
| [4] | CHANDRA S R, AL-DEEK H. Predictions of Freeway Traffic Speeds and Volumes Using Vector Autoregressive Models[J]. |
| [5] | 张亚平,张起森. 高速公路速度—流量模型研究[J]. 中国公路学报,2000,13(3):73-77. ZHANG Ya-ping, ZHANG Qi-sen. A Study of Models of Speed-flow for Freeways[J]. China Journal of Highway and Transport, 2000, 13(3):73-77. |
| [6] | 常成利,周刚. 高速公路路段通行能力分析方法的探索与实践[J]. 公路交通科技,2003,20(2):68-72. CHANG Cheng-li, ZHOU Gang. Research and Practice of Expressway Section Capacity Analysis Method[J]. Journal of Highway and Transportation Research and Development, 2003, 20(2):68-72. |
| [7] | TRACZ M, GACA S. Influence of Various Restrictions on Speed-flow Models[J]. |
| [8] | Transportation Research Board. Highway Capacity Manual[M].Washington, D. C.:TRB, 2010. |
| [9] | ARDEKANI S A, GHANDEHARI M, NEPAL S. Macroscopic Speed-flow Models for Characterization of Freeway and Managed Lanes[J]. Bulletin of the Polytechnic Institute of Jassy, 2011, 57(1):1224-1235. |
 2014, Vol. 31
2014, Vol. 31
