0 引言

我国城市道路交叉口信号控制中，单点信号控制仍处于主导地位^{[1,2,3,4,5,6]}，其重要特性之一即机动车、非机动车和人流构成的混合交通流相互影响，交通冲突点较多，致使国外先进的交通信号控制系统使用性能受限，因此研究适合我国城市的单点信号交叉口混合交通控制模型及方法，是改善城市道路交通拥堵问题的关键^[6]。

国内外现有道路交叉口信号控制方法主要包括三类^{[1,2,3,4,5,6]}：(1) 静态或多时段的定时控制；(2) 感应控制；(3) 智能控制。由于实际交通系统具有随机性、非线性、模糊性等特点，存在数学模型建立困难、算法设计复杂、控制效果及实时性较差等问题，因此智能控制是解决交叉口信号控制的最佳选择，也是目前国内外智能交通领域的研究热点。

现有交叉口智能信号控制方法主要包括专家系统、模糊控制、人工神经网络和进化算法等，其中模糊控制在控制器设计过程中存在模糊规则及隶属度函数选取困难的问题，而人工神经网络控制存在黑箱式学习、训练时间长、可移植性差等缺陷，相比之下进化算法具有并行性、分布式、速度快等优势，更适合于实际交通信号控制。目前国内用于交叉口智能信号控制的进化算法主要为单目标进化算法，包括遗传算法^{[1,2,3,4,5,6,7,8,9]}、梯度算法^[6]、混沌搜索算法^[7]、粒子群优化算法^[10,11]等算法以及其混合算法。沈峰^[12]等首次将第2代经典的多目标进化算法NSGA-II(Non-dominated Sorting Genetic Algorithm)用于交叉口多目标信号控制，取得了较好的优化结果。然而，国内现有智能交通信号控制方法仍存在一定缺陷：(1)遗传算法等单目标智能进化算法仅能对单项交通性能指标，如机动车平均延误或最大通行能力进行最优化控制，即使采用NSGA-II由于算法性能限制也仅能对两项性能指标同时进行优化控制，无法满足实际环境中多项性能指标的控制需求。(2) 现有智能控制方法主要针对交叉口机动车流进行信号控制，没有考虑非机动车和行人的影响，无法适应实际交叉口混合交通流的信号控制需求。(3) 交叉口信号优化控制中当交通性能控制指标个数大于等于3时即属于高维多目标优化问题(Many-Objective Optimization Problems,MOPs)，求解难度极大，目前普遍采用的单目标进化算法和NSGA-II等传统多目标进化算法无法适应求解需求，存在收敛精度低、时耗高甚至求解失败等问题。

针对上述问题，本文设计了综合机动车平均最小延误、平均最小停车次数、最大通行能力、非机动车最小平均延误及行人最小平均等待时间5项交通性能指标的城市道路交叉口高维多目标信号优化控制模型。为成功且高效求解模型,本文设计了基于非Pareto支配的全局排序高维多目标差分进化算法GRMODE (Global Ranking Based Multi-objective Differential Evolution)，通过支配排序策略、密度估计、个体适应度评价等多项关键技术的综合改进，提升国内外现有多目标进化算法的求解精度和运行速度。在南京市某实际交叉口信号控制中的仿真结果表明，本文提出的模型及算法能够获得高峰小时流量水平下更优的信号控制方案，使交通性能指标得到大幅提升，其快速的收敛速度为智能交通信号控制系统的开发及实际应用提供有力保障。

1 交叉口混合交通流模型

交叉口交通信号控制问题就是根据各相位车流量大小及相对绿灯信号的优先权，实现对各相位信号配时和相序安排的合理设置。交叉口信号控制的主要参数为周期时长和每个相位的绿灯时长，通常作为控制系统的输入变量，控制效果一般由交叉口车辆的延误时间、停车次数、通行能力、等待时间等性能指标决定，通常作为控制系统的输出变量^{[1,2,3,4,5,6]}。

1.1 交叉口机动车延误

信号交叉口延误是由于交叉口处信号控制引起交通流间断而损失的车辆行驶时间，目前应用最广的交叉口延误计算方法为美国道路通行能力手册HCM2 000的数学分析模型^[13]。我国常用的交叉口延误计算方法中，须分别估算车道组的每车平均信控延误。进口道每车平均信控延误是进口道中各车由于信号控制而引起车辆在交叉口的延误之加权平均值。整个交叉口的每车平均信控延误是各进口道的每车平均信控延误之加权平均值^[6]。车道组每车的延误估算公式如式(1)所示：

式中，d为车道组每车平均信控延误；d₁为车辆均匀到达时的控制延误，计算公式见式(2)~式(5)： 式中，d_s和d_u分别为饱和延误及非饱和延误;参数C为周期时长;λ为绿信比;X为饱和度;T为分析时段所持续时长;t_u为T中积余车辆的持续时间;Q_b为实测分析期初始积余车辆;C_p为车道通行能力;f_a为绿灯期车流到达校正系数。

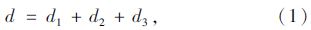
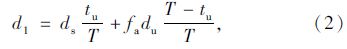
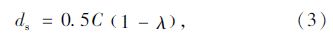
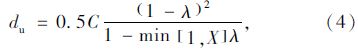
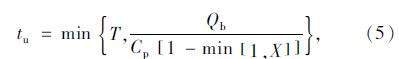
d₂为随机附加延误，即车辆随机到达并引起超饱和周期所产生的附加延误，计算公式如式(6)所示，其中参数e为单个交叉口信号控制类型校正系数，取值为0.5。

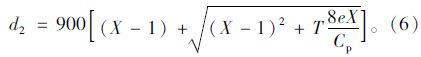
d₃为初始排队附加延误，即在延误分析期初停有上一时段留下积余车辆的初始排队使后续车辆经受的附加延误，计算公式如式(7)所示:

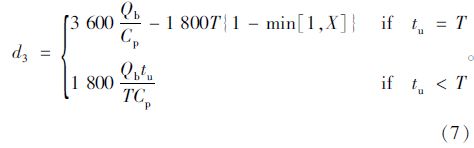
在进口道中车道组延误d基础上加权平均可估算得到进口道的平均信控延误d_A，如式(8)所示：

式中，d_i为进口道中第i车道每车的平均信控延误;q_i为进口道中第i车道的小时交通量换算为其中高峰15 min的交通流率。

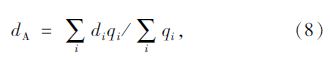
在各进口道延误d_A基础上加权平均可估算得到整个交叉口每车的平均信控延误，如式(9)所示：

式中q_A为进口道的高峰15 min交通流率。

1.2 交叉口机动车停车次数

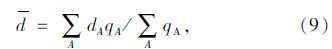
选择通用的Akcelik平均停车率模型^[1]计算进入交叉口每辆车辆的平均停车次数，如式(10)所示：

式中，y为流量比率，即相位对应实际到达流量q与相位饱和流量S的比值；N_s为滞留车辆数，可用式(11)计算得到；C_p为各相位允许通过能力。

1.3 交叉口机动车通行能力

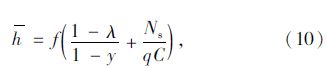
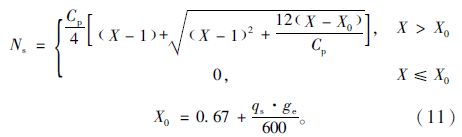
通行能力是指在一定时间内通过交叉口所有进口道停车线车辆数之和。在计算交叉口机动车通行能力时，须分别估算各进口道的机动车通行能力，即进口道中直行、右转、左转车道的机动车通行能力之和。本文采用停车线法计算通行能力^[6]，一条直行车道的通行能力计算公式如式(12)所示：

式中，t_G为直行相位绿灯时间；t_L为一个周期内的绿灯损失时间；t_I为前后两车接连通过停车线的平均间隔时间。

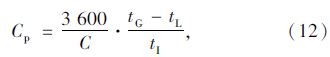
左转专用车道和右转专用车道的通行能力计算公式分别如式(13)、式(14)所示：

式中，t_Gl为一个周期内左转车通过的绿灯时间；v_l和a_l为左转车的通过速度及平均加速度；t_hl为左转车通过停车线断面时的车头时距。 式中，t_Ir为前后两车右转连续通过停车线断面的间隔时间；t_Gr为右转车相位绿灯时间；t_Lr为一周期内右转车的绿灯损失时间。

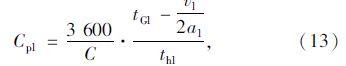
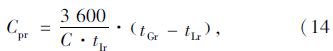
交叉口机动车通行能力为东西南北进口道机动车通行能力之和，计算公式见式(15)：

1.4 交叉口非机动车延误

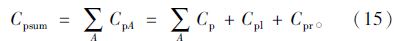
目前我国大中城市的非机动车以自行车为主，我国混合交通流条件下的自行车平均延误计算公式如式(16)所示：

式中，q^b为交叉口自行车的到达流量；q^b_s为车辆驶出停车线的饱和流量；t^b_G为信号绿灯时间；t^b_R为信号红灯时间^[6]。

1.5 交叉口行人过街等待时间

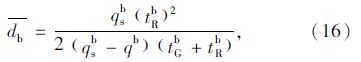
假设交叉口行人的到达是均匀的，则行人过街平均等待时间只与行人过街信号的红灯时间有关，计算公式如式(17)所示:

式中参数t^p_R为行人过街信号的红灯时间^[6]。

2 交叉口高维多目标信号优化控制模型 2.1 高维多目标信号优化控制模型建立

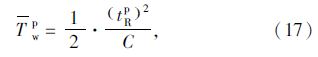
上述交叉口机动车平均延误、平均停车次数、通行能力、非机动车平均延误及行人过街平均等待时间等五项交通信号控制评价指标从不同角度反映了交叉口的服务水平。最佳的信号控制策略应使得五项指标在同一信号控制方案下尽可能同时达到最优，该问题本质上可归结为高维多目标优化问题。国内现有交叉口信号多目标优化控制方法多采用加权求和或乘积^[9,11]的方式将多目标优化问题转化为单目标优化问题进行求解，但容易造成部分指标的局部最优，无法在所有目标上最佳的信号控制方案。

针对这一问题本文设计了交叉口信号控制高维多目标优化模型，输入变量x+[λ₁,λ₂,…，λ_n，C]，包含交叉口n个相位的绿信比及周期，输出变量即效率控制目标函数综合考虑交叉口的机动车平均延误、平均停车次数、通行能力、非机动车平均延误及行人过街等待时间五项指标，对应MOP的五个目标函数分别为：

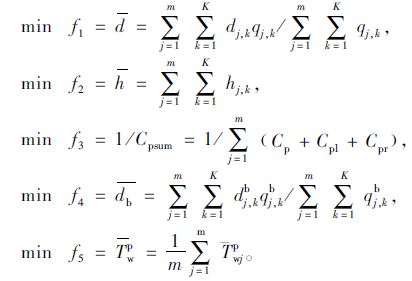
对应的约束条件包括：

(1) 周期约束

式中，C_min为到达车辆全部通过交叉口的周期时间最小值，取值为100 s；C_max为最长信号周期，取值为200 s。

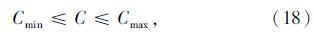
(2) 总时长约束

交叉口各相位有效绿灯时间之和应小于总周期。

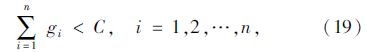
(3) 行人过街等待时间约束

式中^pj_w为交叉口第j方向行人过街平均等待时间。行人过街的平均等待时间应小于某一阈值^p_m，据实际观测取值为180 s。

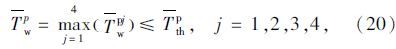
(4) 最大饱和度约束

各相位车流最大饱和度X_i小于1，即：

式中，q_i为第i相位车辆实际流量;k_i为第i相位车道数;q_si为第i相位饱和流量。

2.2 高维多目标信号优化控制模型求解

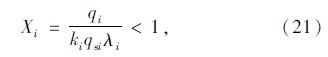
本文针对交叉口混合交通设计的五相位信号优化控制模型包含五项最优化目标，属于高维多目标优化问题，由于计算复杂度高且搜索空间较大，该类问题是目前国内外智能优化领域最难解决的优化问题之一，现有主流解决方法为采用MOEAs。本文在前期MOPs研究基础上设计并提出一种基于非Pareto支配排序的高维多目标进化算法GRMODE，利用其高效的收敛性能求解交叉口交通信号高维多目标控制模型。

高维多目标优化问题求解困难的关键原因在于目标维数的增加导致MOEAs中非支配个体数目急剧上升，精英选择压力减弱，无法从当代种群中选择出优秀的个体进入下一代进化，导致进化过程停滞，表现出随机搜索的特点。GRMODE针对上述问题采用一种新的非Pareto支配排序方法^[14]，即全局排序(Global Ranking,GR)，应用新的评价准则对种群个体进行比较与排序，有效提升选择压力，此外通过全局密度估计、精英选择等多方面的综合改进提升GRMODE的整体求解性能。

(1)GRMODE全局支配排序改进

GRMODE采用新的全局排序机制，个体两两在目标空间中进行比较，定义每个个体X_i的全局排序值GR(X_i)等于该个体在所有目标上与种群中其他个体相应目标值的差值之和，计算公式如式(22)所示：

式中，m为目标维数；f_m为个体在第m个目标上的归一化函数值。根据GR排序机制，对于个体X_i和X_j，若X_i在第m个目标上优于X_j，即f_m(X_i)<f_m(X_j)，则二者差值取值为0，否则差值等于f_m(X_i)-f_m(X_j)。只有当X_i与种群中所有其他个体相比，在所有目标上的差值之和GR (X_i)小于X_j与种群中所有其他个体相比，在所有目标上的差值之和GR(X_j)时，才能够称X_i的收敛性优于X_j。全局排序GR能够综合衡量个体在种群中同其他所有个体之间在各维目标上的差异，只有当某个体在各维目标上的适应度值同其他个体相比整体较优时才被视为优秀个体。该方法能够精确定位种群中每个个体的优劣程度并为其确定全局唯一的排序值，大幅提升了个体等级多样性，有效增强了精英选择压力。

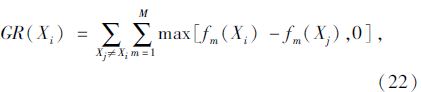
(2)GRMODE全局密度估计改进

GRMODE采用Harmonic平均距离^[15]对种群个体进行全局密度估计，即个体密度值的估计需考虑种群中所有个体的影响。对于种群中的个体X_i，假设目标空间中与其距离最近的k个个体的欧式距离分别为d_i,1,d_i,2,d_i,3，…，d_i,k，则个体X_i的Harmonic平均距离Hd(X_i)见式(23)

为保证在全局范围内对个体拥挤程度进行精确估计，式(23)中的k取值为NP-1，即个体X_i的密度估计考虑种群中除自身外所有个体的影响，由此提高高维情况下个体拥挤密度估计的精确性，促进种群多样性提升。

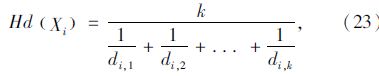
(3)GRMODE精英选择策略改进

GRMODE设计了新的精英选择策略及相应的个体适应值评价方法，综合考虑收敛性指标和分布性指标以决定精英个体的选择。对于种群中个体X_i，假设其在所有目标函数上与种群中其他个体相应目标值的差值之和为GR(X_i)， 且其Harmonic平均距离Hd(X_i)，则其全局适应度值fitness(X_i)如式(24)所示：

式中w₁和w₂为取值{0,1}之间的权系数，用于协调收敛性及分布性的权重。

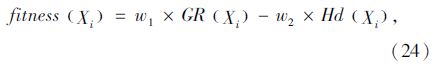
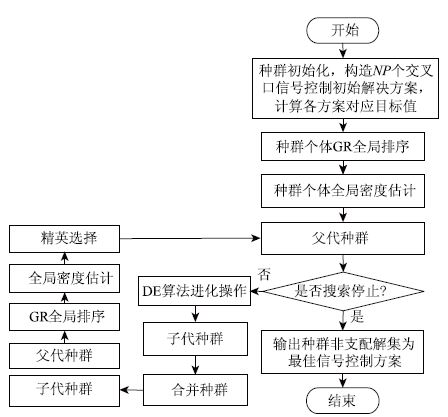
应用GRMODE算法求解交叉口5目标信号优化控制问题的整体流程如图 1所示，具体操作步骤如下：

步骤1：随机生成种群规模为NP初始种群POP1，种群中每一个体向量x=[λ₁,λ₂,…，λ_n,C]代表一组初始信号控制方案，向量x维数为交叉口信号控制相位数目n加1，x中各维变量根据约束条件随机生成。计算种群个体在f₁- f₅上的适应度值。确定算法最大迭代次数Gen。

步骤2：根据2.2节对种群个体进行GR全局排序及全局密度估计。

步骤3：将当前种群作为父代种群。判断是否满足终止条件，若不满足则转到步骤4，否则输出当前种群最优个体集合，即非支配解集作为最终的信号控制方案。

步骤4：对父代种群进行DE进化操作，包括变异、交叉、选择，生成规模为NP的子代种群POP2。

步骤5：合并父代、子代种群，规模为2NP。

步骤6：根据2.2节对合并后种群进行GR全局排序及全局密度估计操作。

步骤7：根据个体排序及密度对合并种群进行精英选择操作，剪切种群至规模NP。转至步骤3。

3 试验设计及结果分析

为测试基于GRMODE算法的交叉口信号控制方法在我国城市交叉口混合交通流情况下的信号控制效果，采用文献^[6]中的实际交叉口案例，即南京市太平北路—珠江路交叉口，在机动车车流高峰小时进行信号控制，该交叉口几何尺寸参数、流量、原始相位绿信比如表 1、表 2、表 3所示。

根据2.1节所述及上述参数建立交叉口5目标信号优化控制模型，利用GRMODE算法对模型进行求解，确定交叉口5目标最优的信号优化控制方案，通过优化交叉口5个相位的绿信比λ₁,λ₂,λ₃,λ₄,λ₅及周期C，实现交叉口机动车平均延误d、平均停车次数h、通行能力C_psum、非机动车平均延误d_b及行人过街平均等待时间T^p_w共5项控制目标的同时最优化。GRMODE算法中种群规模NP取值为10，最大迭代次数Gen取值200，周期C取值范围为[100, 180]，DE算法中变异因子F取值0.5，交叉因子CR取值0.4。

表 4所示为GRMODE算法对交叉口5目标信号优化控制模型的求解结果，由于多目标优化问题的最优解不是单个解而是最优解集，因此表中10项互为非支配的最优解代表交叉口5目标信号优化控制中最优的10项参数设置方案及对应控制目标值。表中，λ₁,λ₂,…,λ₅，分别为第1,2,3,4,5相位的绿信比优化值，C为优化后的信号周期时长，该部分参数为算法GRMODE对模型求解后给出的最优信号控制方案，而每项信号优化控制方案对应的五项控制目标值分别为：d为交叉口机动车的平均延误；h为交叉口机动车的平均停车次数；C_psum为交叉口机动车的通行能力；d_b为交叉口自行车的周期总延误；T^p_w为交叉口行人的平均等待时间。

为衡量本文算法GRMODE与现有其他智能优化算法在同一交叉口上的信号优化控制性能，将GRMODE算法求解5目标信号优化控制模型10次独立运行结果的平均值，与文献^[6]中的多种先进混合算法进行对比，包括遗传算法与梯度法、遗传算法与混沌优化算法、混沌优化算法与梯度法等，试验结果如表 5所示。

从表 5中计算结果可以看出，一方面，GRMODE算法对应的，d，h,C_psum， d_b及 T^p_w等五项信号优化控制目标值不同幅度地优于其他优化算法，说明基于GRMODE算法的5目标信号优化控制方法能够在一定程度上提高交叉口高峰小时流量水平下的机动车通行能力，减小机动车平均延误、平均停车次数、自行车平均延误及行人过街平均等待时间，使交叉口的信号控制效率得到有效提升。另一方面，时效性是衡量交通信号优化控制方法的重要指标，现有遗传算法等传统智能优化算法因在高维多目标优化问题求解上精度低、速度慢，因此无法适应多目标环境下的实际交通信号控制需求，在一定程度上影响了智能交通信号控制系统的开发和应用。本文设计算法GRMODE充分考虑了运算速度对于算法性能的影响，在上述交叉口的五项目标信号优化控制计算中，能够保证在获得全局最优解集的条件下，算法独立运行统计平均耗时仅4.81 s，有效提升了现有智能优化算法在高维多目标优化问题求解中的运算速度，有利于本文设计模型及算法在实际交通工程中的应用。

4 结论

针对我国城市道路交叉口现有混合交通流智能信号控制方法控制效率较低的问题，提出了一种交叉口高维多目标信号优化控制模型，通过交叉口信号配时实现机动车平均延误、停车次数、通行能力、非机动车平均延误及行人等待时间等多项性能指标的同时最优化控制。为高效求解模型的高维多目标优化控制问题，本文设计了新的高维多目标进化算法，包括新的高维多目标进化算法模型及改进Pareto支配排序等多项关键技术改进，克服国内外现有同类算法求解精度低、计算时耗大、不适用于实际工程优化等缺陷。在交叉口环境下的信号控制仿真试验结果表明，本文方法能够大幅提升交叉口混合交通流高峰小时流量水平下的智能信号控制效率且具有较短的运行时间，为交叉口智能系统的开发与研究提供了必要的理论支持。