扩展功能
文章信息
- 李生杰, 杨晓华, 李玄哲
- LI Sheng-jie, YANG Xiao-hua, LI Xuan-zhe
- 乌鞘岭公路隧道破碎岩体段结构可靠性评价
- Evaluation of Structural Reliability of Broken Rock Mass Section of Wushaoling Highway Tunnel
- 公路交通科技, 2014, Vol. 31 (11): 96-102
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (11): 96-102
- 10.3969/j.issn.1002-0268.2014.11.016
-
文章历史
- 收稿日期:2013-8-14
2. 甘肃路桥公路投资有限公司, 甘肃 兰州 730000;
3. 陕西省电力设计院, 陕西 西安 710054
2. Gansu Luqiao Highway Investment Co., Ltd., Lanzhou Gansu 730000, China;
3. Shaanxi Electric Power Design Institute, Xi'an Shaanxi 710054, China
隧道施工和运营中环境复杂,地质条件,材料性能,几何参数及荷载均具有随机不确定性,对隧道结构的可靠性有很大影响。目前,对铁路隧道结构可靠性已经有了较多研究,文献[1, 2, 3, 4]研究了铁路隧道衬砌结构可靠指标计算的原则和方法。景诗庭全面总结了地下结构概率极限状态设计方面的研究。文献[5, 6]将可靠度理论引入铁路隧道结构设计,使隧道结构设计方法实现了由半概率法向近似概率法的过渡,但对于公路隧道设计有一定局限性,基于可靠度理论的概率极限状态设计方法尚不成熟[7]。尤其针对公路隧道穿过围岩条件差的结构可靠性的研究相对较少。公路隧道在穿过破碎岩体段时,围岩自稳能力更差,本文针对乌鞘岭隧道破碎岩体段,以可靠性理论为基础,对施工过程中试验所得的围岩,初期支护和二次衬砌的物理力学参数进行统计分析,得到每个参数的均值,方差和分布类型,结合ANSYS有限元软件建立模型进行随机有限元分析得到结构可靠度,并对其进行灵敏度分析评价,得到对类似工程设计有意义的结论。
1 建立计算模型乌鞘岭隧道局部区段,通过区域逆断层,断层破碎带宽度300 m,与隧道轴线近直交,断层倾向与洞线前进方向基本一致,上盘为奥陶系变质岩,下盘为三叠系砂岩、砾岩,组成物主要为压碎岩、角砾岩及靡棱岩,围岩级别属于Ⅴ级。在断裂与下盘地层接触地带,隧道开挖过程中洞身岩体易产生较大塑性变形,本文研究段隧道最大埋深189 m;隧道开挖轮廓为15.53 m×11.35 m,施工采用短台阶法。
目前,隧道结构分析所采用的模型主要有荷载-结构模型,连续介质模型,工程类比法和以现场量测和实验室试验为主的实验室模型试验,收敛约束模型等分析方法。其中,对于本文围岩破碎段支护类型,喷锚支护和复合式衬砌比较适合的理论方法是连续介质模型,《公路隧道设计结构规范》(JTGD70—2004)指出,复合式衬砌的二次衬砌理论上应按地层结构法计算。因而,以连续介质模型为基础,进行公路隧道结构可靠性分析是合理的[8]。
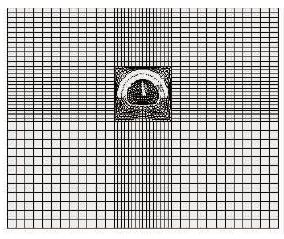
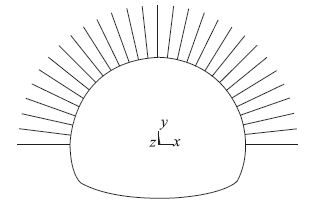
本文在连续介质模型的计算方法中选择有限元法(FEM),将衬砌和围岩作为一个统一承载系统,一起承受外界载荷,根据隧道设计的支护衬砌的形式,认为岩体受力和变形为弹塑性的,衬砌材料视为弹性体,使用Drucer-Prager屈服准则,按照非线性弹塑性有限元模型模拟开挖和支护过程,由于围岩极为破碎,设计采用锚喷支护,分析隧道结构非线性受力和变形特征,模拟计算模型如图 1、图 2所示。
|
| 图 1 整体模型 Fig. 1 Integrated model |
|
| 图 2 锚喷支护模型 Fig. 2 Model of bolt-shotcrete support |
建立计算模型后,对隧道结构不确定性因素量化时,本文选用的变量为随机变量,不确定变量描述选用的模型为概率模型。由于初支钢拱架是提前制作完成,其性能可控性较强,在建立计算模型时,将钢拱架(I20a型钢支护间距75 cm)作为定量,经过对施工时试验数据统计计算,根据文献[1],本文所考虑的各随机变量的均值,标准差分布类型见表 1。
| 项目 | 均值 | 标准差 | 分布类型 | |
| 围岩 | 变形模量/Pa | 1.11e9 | 0.249 1e9 | 正态分布 |
| 密度/(kg·m-3) | 250 0 | 65.22 | 正态分布 | |
| 泊松比 | 0.38 | 0.356~0.410 | 均匀分布 | |
| 黏聚力/Pa | 0.125e6 | 0.0167e6 | 正态分布 | |
| 内摩擦角/(°) | 25 | 1.43 | 正态分布 | |
| 初支 | 密度/ (kg·m-3) | 2 200 | 386 | 正态分布 |
| 弹性模量/Pa | 29.3e9 | 3.96e9 | 正态分布 | |
| 厚度/m | 0.26 | 0.0614 | 对数正态分布 | |
| 泊松比 | 0.2 | 0.192~0.220 | 均匀分布 | |
| 锚杆 | 弹性模量/Pa | 210e9 | 13.1e9 | 正态分布 |
| 泊松比 | 0.31 | 0.277~0.322 | 均匀分布 | |
| 密度/ (kg·m-3) | 7 800 | 204 | 正态分布 | |
| 二衬混凝土 | 弹性模量/Pa | 31.105e9 | 1.661e9 | 正态分布 |
| 密度/(kg·m-3) | 2 402 | 71 | 正态分布 | |
| 厚度/m | 0.5 | 0.062 | 对数正态分布 |
在实际工程中,所做的室内试验数据和现场试验的数据是非常有限的,根据文献[9]的分析,本文在随机有限元结构可靠度分析方法中选用蒙特卡罗法。文献[10]证明,Latin hypercube抽样比伪随机数法所得到的计算结果稳定且效率高,统计量方差小,在抽样计算中选择Latin hypercube抽样方法。在得到各个随机变量概率分布类型和数字特征(表 1)之后,将随机变量特征值和分布类型输入已建立好的计算模型后,样本尺寸取3 000个,模型抽样计算后获得进行结构可靠度计算时所需的主要随机变量样本值,生成输出随机变量样本的直方图。
|
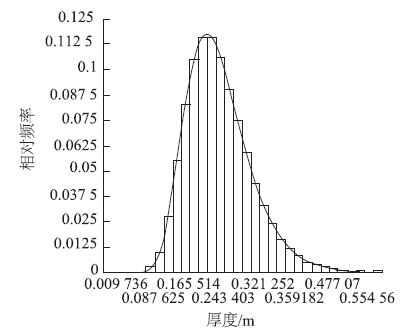
| 图 3 初支厚度的直方图 Fig. 3 Histogram of primary support thickness |
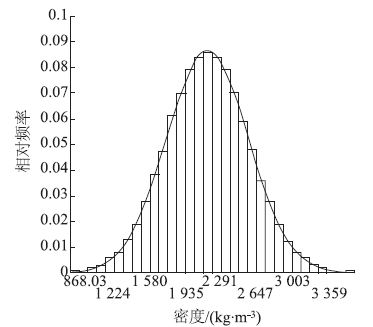
现以喷射混凝土厚度和喷射混凝土密度为例,其直方图分别为图 4和图 5。
|
| 图 4 初支密度直方图 Fig. 4 Histogram of primary support density |
|
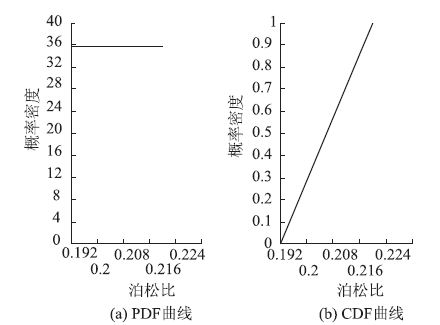
| 图 5 围岩泊松比PDF和CDF曲线 Fig. 5 PDF and CDF curves of Poissons ratio of surrounding rock |
由图 3和图 4可以看出,拟合曲线均比较光滑,而且抽样数据各个子序列均有数据且无间隙,表明所进行的随机抽样的样本量充分,可作为进行结构可靠性计算的随机变量样本,其余随机变量直方图拟合曲线均光滑满足要求。
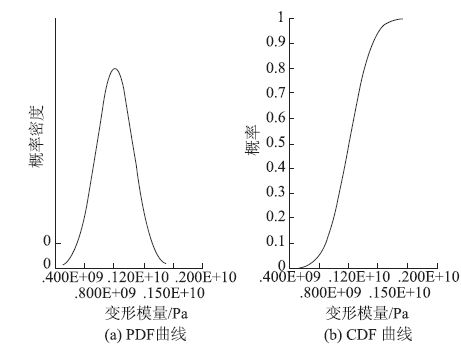
围岩,喷射混凝土,二次衬砌的泊松比均服从均匀分布,上下界是已知的,以围岩的泊松比为例,其概率密度曲线(PDF)和概率分布曲线(CDF)图如图 5所示;喷射混凝土和二次衬砌的厚度均服从对数正态分布,以喷射混凝土厚度为例,其PDF和CDF图如图 6所示;其他随机变量均服从正态分布,以围岩变形模量为例,其PDF和CDF曲线,如图 7所示。

|
| 图 6 初支厚度PDF和CDF曲线 Fig. 6 PDF and CDF curves of primary support thickness |
|
| 图 7 围岩变形模量PDF和CDF曲线 Fig. 7 PDF and CDF curves of deformation modulus of surrounding rock |
结构可靠度是表征结构在规定时间内和规定的条件下完成预定功能的概率[11],其中的预定功能通常以极限状态作为标志,极限状态可用极限状态方程来描述:
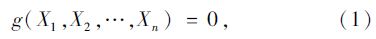

在ANSYS软件概率计算模块中,将随机变量样本带入结构功能函数,得到功能函数解的样本,统计隧道结构失效的次数[12]。根据Bernoulli大数定理,n重Bernoulli试验中,当趋于无穷时,随机事件发生的频率fn依概率收敛于p,即:
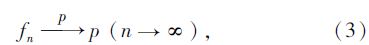
因此,可以将大量随机抽样中结构失效发生的次数占总抽样数的频率作为隧道结构失效概率,从而得到可靠度。随机有限元模型计算后可以得到锚杆轴力、初期支护喷射混凝土、二次衬砌混凝土内力的分布直方图,概率分布曲线并计算出可靠度,同时分析了每一个应力的灵敏度。
4.1 初支可靠度及灵敏度计算
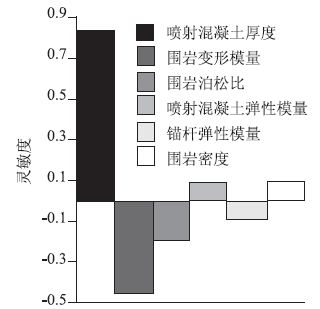
喷射混凝土最大弯曲拉应力直方图和喷射混凝土最大弯曲拉应概率分布曲线如图 8和图 9所示,根据《公路隧道设计规范》(JTG D70—2004),C25喷射混凝土最大弯曲拉应力容许值为0.5 MPa,经计算小于该值的概率为74.827 6%,失效概率为25.172 4%,即喷射混凝土最大弯曲拉应力可靠度为74.827 6%,图 10纵轴为Spearman秩相关系数rs(显著性水平取2.5%),横轴是各随机变量对喷射混凝土最大弯曲拉应力的影响程度,即灵敏度,从左至右依次减小,分别是喷射混凝土厚度,围岩变形模量,围岩泊松比,喷射混凝土弹性模量,锚杆弹性模量,围岩密度,且喷射混凝土的厚度对初期支护最大弯曲拉应力的影响最大。

|
| 图 8 初支最大弯曲拉应力直方图 Fig. 8 Histogram of maximum bending tensile stress of primary support |

|
| 图 9 初支最大弯曲拉应力概率分布曲线 Fig. 9 Probability distribution curves of maximum bending tensile stress of primary support |
|
| 图 10 初支最大弯曲拉应力灵敏度 Fig. 10 Sensitivity of maximum bending tensile stress of primary support |
|
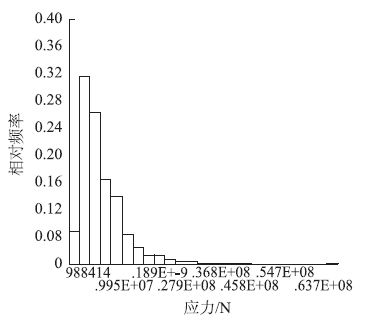
| 图 11 初支最大弯曲及偏压应力直方图 Fig. 11 Histogram of maximum bending and bias stress of primary support |
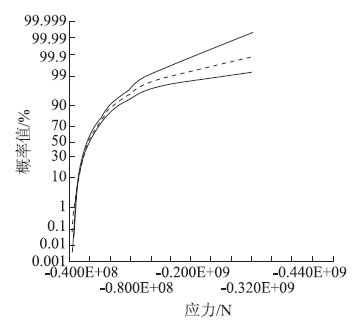
C25喷射混凝土最大弯曲及偏压应力容许值为9.6 MPa,经计算,如图 12和图 13所示,小于该值的概率为76.58%,即可靠度为76.58%,失效概率为23.42%。表明本段隧道喷射混凝土最大弯曲及偏压应力可靠度较低。图 13纵轴为Spearman秩相关系数rs(显著性水平取2.5%),横轴是各随机变量对喷射混凝土最大弯曲及偏压应力的灵敏度,从左至右依次减小,分别是喷射混凝土厚度,围岩变形模量,喷射混凝土弹性模量,围岩密度,围岩泊松比,且喷射混凝土的厚度对初期支护最大弯曲及偏压应力的影响最大。
|
| 图 12 初支最大弯曲及偏压应力概率分布曲线 Fig. 12 Probability distribution curves of maximum bending and bias stress of primary support |

|
| 图 13 初支最大弯曲及偏压应力灵敏度 Fig. 13 Sensitivity of maximum mending and bias stress of primary support |
锚杆最大轴力容许值为230 MPa,经计算,如图 14、图 15所示,锚杆最大轴力失效概率为21.854 9%,可靠度为78.145 1%。锚杆所受的应力较大,这与本段隧道穿过破碎岩体有直接关系,由此也可以看出,锚杆在本段隧道的支护中所发挥的作用也是非常显著的。图 16纵轴为Spearman秩相关系数rs(显著性水平取2.5%),横轴是各随机变量对锚杆最大轴力的灵敏度,从左至右依次减小,分别是喷射混凝土厚度、喷射混凝土弹性模量、锚杆弹模、喷射混凝土泊松比。

|
| 图 14 锚杆最大轴力直方图 Fig. 14 Histogram of maximum axial force of anchor |

|
| 图 15 锚杆最大轴力概率分布图 Fig. 15 Probability distribution curves of maximum axial force of anchor |

|
| 图 16 锚杆最大轴力灵敏度 Fig. 16 Sensitivity of maximum axial force of anchor |
如图 17~图 20所示,C30二次衬砌最大弯曲拉应力和最大弯曲及偏心受压应力容许值分别为0.5 MPa 和11.2 MPa,计算后,最大弯曲拉应力和最大弯曲及偏心受压应力计算值全部远远小于容许值,在计算过程中所取的置信度水平为0.95,因此二衬最大弯曲及偏心受压应力和弯曲及偏心受压应力的可靠度均为95%,表明二次衬砌所受相对较小,隧道处于安全状态。

|
| 图 17 二衬最大弯曲拉应力直方图 Fig. 17 Histogram of maximum bending tensile stress of secondary lining |

|
| 图 18 二衬最大弯曲拉应力概率分布曲线 Fig. 18 Probability distribution curves of maximum bending tensile stress of secondary lining |

|
| 图 19 二衬最大弯曲及偏心受压应力直方图 Fig. 19 Histogram of maximum bending and bias stress of secondary lining |

|
| 图 20 二衬最大弯曲及压应力概率分布曲线 Fig. 20 Probability distribution curves of maximum bending and bias stress of secondary lining |
(1)建立随机有限元分析模型的基础上,得到随机变量的直方图,PDF和CDF曲线,验证了抽样规模满足分析的需要。
(2)通过随机有限元的计算分析,得到本段隧道初期支护结构可靠度为76.580 0%,锚杆可靠度为78.145 1%,所受应力均较大,其可靠度相对较低,灵敏度分析中表明喷射混凝土厚度,围岩变形模量对二者的影响最为显著,这与本段隧道围岩破碎有直接关系。
(3)计算结果表明,二次衬砌可靠度为95%,二衬为安全储备,所受应力相对较小,拉应力和压应力均在容许值范围之内,所以本段隧道整体处于安全状态。
(4)由于隧道在建设过程中,不管是从地质环境、隧道设计还是施工过程中都有很多不确定因素影响着隧道结构的可靠性大小,通过本文的计算为后期隧道的建设和运营维护提供科学依据。
| [1] | 宋玉香,景诗庭,刘勇.单线电气化铁路隧道衬砌结构目标可靠指标的试算分析[J].岩石力学与工程学报,1999,18(1):46-49. SONG Yu-xiang,JING Shi-ting,LIU Yong. Calculation of Object Reliability Index of Tunnel Lining Structure for Single Track Electrification Railway[J]. Chinese Journal of Rock Mechanics and Engineering,1999,18(1):46-49. |
| [2] | 高波,蔺安林,赵万强.隧道衬砌结构可靠指标计算方法的研究[J].西南交通大学学报,1996,31(6):584-589.GAO Bo,LIN An-lin,ZHAO Wan-qiang.Research on Computation Methods for Structural Reliability Index of Tunnel Lining[J]. Journal of Southwest Jiaotong University,1996,31(6):583-589. |
| [3] | 谭忠胜,高波,关宝树.偏压隧道衬砌结构可靠度分析[J].西南交通大学学报,1996,31(6):595-601.TAN Zhong-sheng,GAO Bo,GUAN Bao-shu.The Structural Reliability Analysis of Bias Tunnel Lining[J]. Journal of Southwest Jiaotong University,1996,31 (6):595-601. |
| [4] | GB50216-94,铁路工程结构可靠度设计统一标准[S].GB50216-94,Unified Design Standard for Reliability of Railway Engineering Structures[S]. |
| [5] | TB 10003—2001 J117—2001,铁路隧道设计规范[S].TB 10003—2001 J117—2001,Code for Design of Railway Tunnel[S]. |
| [6] | TB 10003—2005,铁路隧道设计规范[S].TB 10003—2005,Code for Design on Tunnel of Railway[S]. |
| [7] | 魏新欣,丁文其.公路隧道概率极限状态设计方法[J].公路交通科技,2011,28(10):75-79.WEI Xin-xin,DING Wen-qi. Probabilistic Limit State Design Method of Highway Tunnel[J].Journal of Highway and Transportation Research and Development,2011,28(10):75-79. |
| [8] | 杨建国,谢永利,李俊升,等.隧道结构可靠性研究进展[J].现代隧道技术,2009,46(6):1-7.YANG Jian-guo,XIE Yong-li,LI Jun-sheng,et al. Progress in Research on Tunnel Structural Reliability[J].Modern Tunnelling Technology,2009,46(6):1-7. |
| [9] | 梅刚.基于非线性随机有限元的结构可靠度问题研究[D].北京:清华大学,2005.MEI Gang. Research on Structure Reliability Based on Nonlinear Stochastic Finite Element[D].Beijing:Tsinghua University,2005. |
| [10] | 张清,王东元,李建军.铁路隧道衬砌结构可靠度分析[J].岩石力学与工程学报,1994,13(3):209-218. ZHANG Qing,WANG Dong-yuan,LI Jian-jun. Reliability Analysis of Lining Structures in Chinese Railroad Tunnels[J].Chinese Journal of Rock Mechanics and Engineering,1994,13(3):209-218. |
| [11] | 李飞.钢管混凝土柱的可靠度与优化分析[D].西安:西安理工大学,2008.LI Fei. Analysis of Reliability and Optimization of Concrete Filled Steel Tubular Column[D].Xi'an:Xi'an University of Technology,2008. |
| [12] | 武清玺.结构可靠性分析及随机有限元-理论、方法、工程应用及程序设计[M].北京:机械工业出版社,2005.WU Qing-xi.Structural Reliability Analysis and Stochastic Finite Element: Theory,Method,Engineering Application and Program Design[M].Beijing:China Machine Press,2005. |
 2014, Vol. 31
2014, Vol. 31
