扩展功能
文章信息
- 陈宇, 贾艳敏
- CHEN Yu, JIA Yan-min
- 预应力混凝土T梁在施工阶段的挠度和边界条件分析
- Analysis on Deflection and Boundary Conditions of PC T-beam in Construction Phase
- 公路交通科技, 2014, Vol. 31 (11): 78-84
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (11): 78-84
- 10.3969/j.issn.1002-0268.2014.11.013
-
文章历史
- 收稿日期:2014-3-8
后张法预应力混凝土预制装配梁在完成张拉预应力钢筋以前,构件必须放置在施工平台上,若在张拉前事先设置支座支撑,跨度较大的混凝土梁会由于截面上恒载弯矩较大而底缘开裂[1]。Mircea I. PSTRAV [2]对预应力混凝土T形梁进行了全面的试验,所测挠度是预应力钢筋张拉完毕后设置支座的简支梁。梁智殷、薛伟辰[3]在体外预应力混凝土组合梁受力性能研究中采用的是简支体系,为防止混凝土上表面在预应力张拉阶段出现反拱开裂,试验加载过程分为三个阶段,所测挠度是简支梁跨中位置。
曾丁[4]等对后张有黏结预应力混凝土梁做了疲劳预应力钢筋损失试验,是在简支情况下进行的。梁体在使用阶段的边界条件为简支,但这与构件在施工时所处的实际受力状态有所差别。国内实际施工时的情况是张拉前构件底面与施工平台紧密接触,在张拉过程中梁底面逐渐脱离施工平台,经吊装就位后形成简支体系。所以本文针对预加力阶段梁的边界条件以及其受力状态展开分析和讨论。
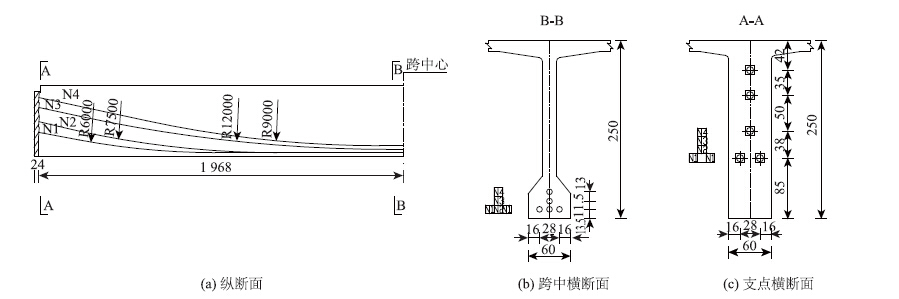
1 试验梁本试验桥是在建的内蒙古宝贝河桥,采用简支转连续结构。根据试验桥设计资料,已知:后张法一端张拉一端锚固;施工梁长39.28 m,梁自重集度(包括横隔板)取平均值g=28.1 kN/m;预应力钢筋采用1×7股d=15.2 mm的钢绞线;N3,N4束形为圆曲线,N1,N2束形为圆曲线与直线组合,钢绞线布置如图 1所示;张拉控制力Ncon=193.9 kN,试验梁分批张拉:N3 50%→N2 50%→N1右50%→N1左100%→N1右100%→N2 100%→N3 100%→N4 100%。
|
| 图 1 预应力钢筋布置(单位:cm) Fig. 1 Layout of prestressed rebars(unit:cm) |
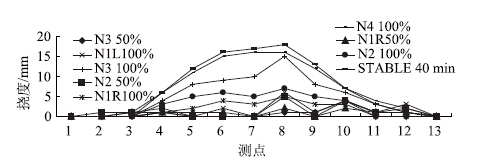
图 2为试验桥施工现场试验准备,在梁顶板、腹板等位置布置了应变片,在试验梁纵向布置13个挠度测点,各个张拉阶段的测点挠度如图 3所示。

|
| 图 2 试验梁 Fig. 2 Test beam |
|
| 图 3 张拉阶段反向挠度 Fig. 3 Reverse deflection in tensioning phase |
梁与施工平台的接触,属于面与面的摩擦接触问题,摩擦力阻止两个物体的切向滑动。接触面的相互作用包括两个部分:一是接触面的法向作用,即压力;另一个是接触面的切向作用,即摩擦力。只有当两个表面发生接触时才会产生约束,当两个表面分离时约束瞬间消失,而且在此瞬间接触间隙由闭到开,接触压力会发生剧烈变化,所以摩擦接触的约束是不连续的[5]。
即使在有限元计算当中,也必须假设出一个初始状态,若计算时发生与初始条件不符,将重新假设初始状态,反复迭代直至符合:在接触迭代过程中,由于接触单元的接触状态及接触面上的应力和变形都是未知的,因此,开始计算时,要假定一种初始接触状态,计算此状态下的应力和变形。如果计算得到的应力和变形与假定的接触状态不符,则修改接触状态,进行下一步迭代,直至应力与变形相符则此加载级计算收敛,可进行下一加载级的迭代计算[6]。
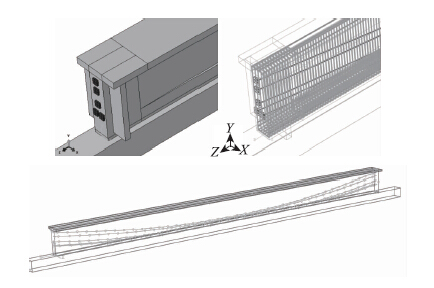
2.2 有限元模型为了分析梁与施工平台摩擦接触,利用ABAQUS建立有限元模型:混凝土本构关系由Concrete Damage Plastic来定义[, ],各参数根据施工实测值换算代入;混凝土梁采用实体单元C3D8R,为使得计算收敛,与台座接触面层的实体单元采用C3D8I[6];预应力钢筋采用T3D2只受拉力的弹性单元,并定义温度膨胀系数,利用降温法施加预应力[12];普通钢筋采用T3D2并定义既能受压又能受拉的塑性单元。施工平台定义为C3D8I单元,弹性模量为钢材的100倍,台座刚度很大,几乎不发生变形;利用Interaction模块中Contact定义摩擦接触。预加力阶段梁ABAQUS有限元模型如图 4所示。
|
| 图 4 预加力阶段梁ABAQUS有限元模型 Fig. 4 ABAQUS finite element model of beam in prestressing phase |
在张拉阶段,混凝土梁承受的作用有施工平台的反向压力、自重和预加力。梁的边界条件为有压力的摩擦接触,施工平台底面固结。梁底面与台施工平台顶面的接触定义为小滑移,分别试算了光滑接触和摩擦接触,计算结果表明,由于混凝土和钢板这两种材料之间的摩擦系数较低(一般为0.035),摩擦力对梁的水平位移影响甚微。
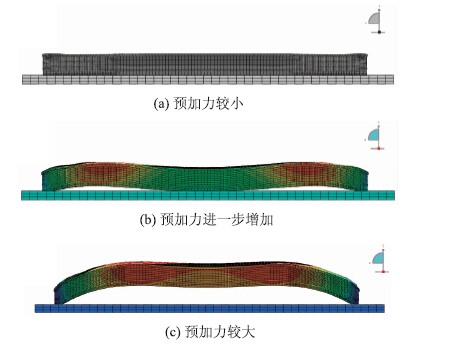
计算时采用多步分析,荷载分级施加,得到了各级荷载下的几种典型的接触状态:一是预加力较小时,接触面无间隙变化,梁与施工平台紧密接触,节点微小的竖向位移是由于混凝土弹性压缩引起,见图 5(a);二是预加力进一步增加后,接触面一部分由闭到开,脱离台面的梁段反向挠曲变形,但由于跨中区域的恒载弯矩较大梁被压回平台,张拉及锚固端预应力钢筋在截面形心轴上方将梁压在平台上,见图 5(b);三是预加力较大时,张拉及锚固端布置在截面形心轴下方的预应力将梁顶起,除了端点一个单元长度范围内的梁体与台座接触,其他区域均离开台座,此时边界条件近似为简支,见图 5(c)。
|
| 图 5 预加力阶段梁与台座的接触状态 Fig. 5 Contact status between beam and construction platform in prestressing phase |
ABAQUS standard隐式分析计算代价很高,而ABAQUS explicit显式分析对接触分析是高效的,不需要迭代计算[13],但利用显式分析计算要求定义施荷速度,经过大量的试算,预应力钢筋张拉时的加载速度对计算结果影响极大。所以在预应力钢筋张拉过程中,要精确判断梁与施工平台的接触细节是十分困难的,但是张拉稳定后平衡状态下的接触状态是可以确定的。
3 基本假设为了进一步分析平衡状态下边界条件的规律,在预加力瞬间,假设一个初始状态。根据上述有限元计算的各个接触状态,作如下基本假设:
(1)预加力阶段梁为弹性体;
(2)小变形,无几何非线性;
(3)梁在预加力瞬间可发生挠曲变形,初始状态为简支,而后在预加力、自重作用下边界条件重分布,并在台座反力的作用下变形稳定并达到平衡;
(4)变形后的梁是否与台座接触取决于初始状态下挠度。
后张法预加力阶段混凝土和预应力筋未形成有效的黏结,为无黏结预应力构件,可用等效荷载来分析混凝土梁的受力。等效荷载是一个自平衡力系,从构件中脱离出来的预应力钢筋处于静止的平衡状态,预应力钢筋受到一个平衡力系的作用,预应力钢筋对结构的反作用必是一个自平衡力系[, ]。
在施预加力前,放置于平台上的梁处于自重和平台反力的平衡状态,施预加力后相当于对构件叠加一个自平衡力系,所以梁仍处于平衡状态。但在预加力瞬间,平台反力与接触域会重分布,若在某个区域接触面由闭到开,自重弯矩随即发生作用。所以从预加力开始到平衡可分为三个阶段。
第一阶段:预加力突施打破原有平衡,梁发生变形,瞬间的边界条件为简支;
第二阶段:边界条件突变重分布,梁脱离台座的那部分自重弯矩发生作用;
第三阶段:梁在预加力、自重和台座反力的作用下重新平衡。
重新平衡后边界条件的最终结果有三种情况:
(1)预加力较小,由预加力产生的梁挠曲变形部分与自重作用产生的变形平衡,表面上梁没有挠曲变形;
(2)预加力增大一定程度时,在跨中至梁端一部分区域由预加力作用产生挠曲,而跨中附近由于自重弯矩作用较大由预加力作用产生挠曲压回平台;
(3)预加力较大,梁端与平台接触,全梁产生挠曲变形。
4 张拉阶段挠度分析根据参考文献[1, 16, 17]中梁挠曲变形与构件截面上的总弯矩值的关系,建立预加力阶段的挠度计算表达式。
若存在区间(x1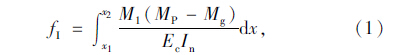
本文以直线配筋和曲线配筋为例,以梁左端形心轴处为坐标系原点,施工梁长设为l,规定使梁发生向上变形的弯矩为正,若梁与台座之间存在接触长度,定义为lf,运用参考文献[14]中关于等效荷载的基本性质,分析构件的边界约束条件。
4.1 直线配筋一般地,如图 6(a)所示,存在x=x1,使得在此处Mp(x1)=Mg(x1)。设跨中有区域lf与平台接触,重分布后在接触区lf内M1=0,除端点以外的其他截面M1>0,则:
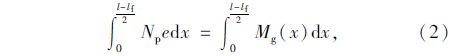
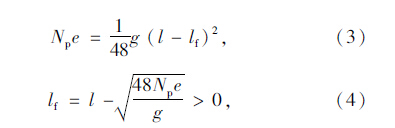
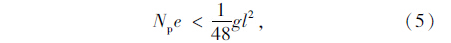
当预加力较大,打破原有平衡后全梁能够维持反向挠曲变形,M1>0。则:
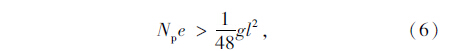
综上所述,直线配筋情况下,构件的边界条件为:
当Npe>148gl2,梁的两端点简支;
当Npe<148gl2,梁的梁端点简支,跨中存在lf与平台接触。
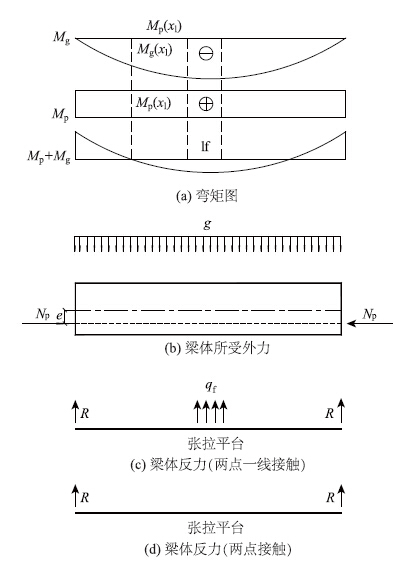
|
| 图 6 直线配筋 Fig. 6 Straight linetype reinforcement |
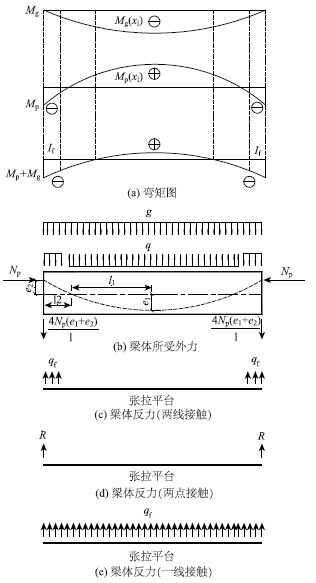
一般地,如图 7(a)所示,存在x=x1,使得在此处Mp(x1)= Mg(x1), 设端点附近有区域lf与平台接触,重分布后在接触区lf内M1=0,除lf区域以外的其他截面M1>0,则:
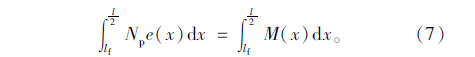
式(7)是关于的一元三次方程,通过编制程序可解得lf。该式成立的条件为:
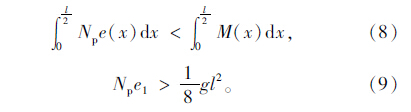
当同时满足式(8)、式(9),平衡后的边界条件为两端点附近lf与平台接触,即两线接触,见图 7(c); 若不满足式(8),平衡后的边界条件为两端点简支,即两点接触,见图 7(d);若不满足式(9),平衡后构件整个底面与平台接触,即一线接触,见图 7(e)。
|
| 图 7 曲线配筋 Fig. 7 Curve linetype reinforcement |
计算时考虑三种典型工况: 工况1,N3 50%; 工况2,N1右50%,N2 50%,N3 50%; 工况3,全部张拉100%并稳定40 min;
张拉过程中在锚固端一侧,由于管道摩阻力产生的预应力损失较大,计算值与实测值均取用张拉端一侧的数值,并且不考虑由于分批张拉对边界条件产生的影响。圆曲线束形近似按二次抛物线处理。并设:
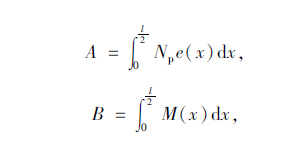
计算结果列于表 1~表 3。通过理论计算确定的边界条件,有限元计算结果以及实测结果基本吻合,验证了计算基本假设的合理性,故运用静力分析和挠曲变形规律得到的计算方法是可行的。
| 工况1 | Ai | ∑Ai | B | 边界条件 | lf/m | ||
| 理论值 | 有限元 | 实测值 | |||||
| N1左 | 0 | ||||||
| N1右 | 0 | ||||||
| N2 | 0 | 18 595 | 141 918 | III | 39.28 | 39.28 | 39.28 |
| N3 | 18 595 | ||||||
| N4 | 0 | ||||||
| 工况2 | Ai | ∑Ai | B | 边界条件 | lf/m | ||
| 理论值 | 有限元 | 实测值 | |||||
| N1左 | 0 | ||||||
| N1右 | 35212 | ||||||
| N2 | 31645 | 85 452 | 141 918 | I | 2.8 | 2.3 | 1.6 |
| N3 | 18 595 | ||||||
| N4 | 0 | ||||||
| 工况2 | Ai | ∑Ai | B | 边界条件 | lf/m | ||
| 理论值 | 有限元 | 实测值 | |||||
| N1左 | 70424 | ||||||
| N1右 | 70424 | ||||||
| N2 | 63290 | 277 116 | 141 918 | II | 0 | 0.2 | 0.5 |
| N3 | 37190 | ||||||
| N4 | 35788 | ||||||
通过直线配筋和曲线配筋情况下的受力分析,推导了梁的接触约束情况及其边界条件。在预加力阶段,预应力混凝土梁的边界条件主要与预应力钢筋线型、纵断面位置,预加力大小以及构件自重集度有关。由于受力分析过程中初始状态是基于接触分析中的基本假设,并且等效荷载对梁的效应只是近似的,本文进行实例计算来验证基本假设在受力分析中的合理性,比较边界条件中的接触长度lf的理论计算值、有限元计算值与实测值。
本文讨论的预应力混凝土梁在预加力阶段的边界条件分析中得到如下结论:
(1)梁与台座有三种典型的接触状态:一是预加力较小时,接触面无间隙变化;二是预加力进一步增加后,一部分梁体脱离台面的梁段能维持反向挠曲变形;三是预加力较大时,除了梁端处的区域与平台接触,其他区域均离开平台。
(2)梁的边界条件主要与预应力钢筋线型、纵断面位置,预加力大小以及构件自重集度有关。
(3)通过分析推导,得到了直线配筋和曲线配筋情况下的边界条件。
| [1] | 贾艳敏,高力. 结构设计原理[M]. 北京: 人民交通出版社,2004. JIA Yan-min,GAO Li. Principle of Structure Design[M]. Beijing: China Communications Press,2004. |
| [2] | PSTRAV M I. Full Scale Test of a Prestressed Concrete T-Beam[J]. Acta Technica Napocensis: Civil Engineering & Architecture,2011,54(1): 50-59. |
| [3] | 梁智殷,薛伟辰. 体外预应力 FRP-混凝土组合梁受力性能研究[J]. 公路交通科技,2013,(12): 241- 244. LIANG Zhi-yin,XUE Wei-chen. Research for Force Capacity of External Prestressed FRP-Concrete Composite Beam[J]. Journal of Highway and Transportation Research and Development,2013,(12): 241-244. |
| [4] | 曾丁,王国亮,谢峻,等. 预应力混凝土梁疲劳预应力损失探索性试验[J]. 公路交通科技,2012,29(12): 79-83. ZENG Ding,WANG Guo-liang,XIE Jun,et al. Exploratory Experiment of Fatigue Prestress Loss of Prestressed Concrete Beam[J]. Journal of Highway and Transportation Research and Development,2012,29(12): 79-83. |
| [5] | 庄茁,张帆,岑松. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社,2005. ZHUANG Zhuo,ZHANG Fan,CEN Song. Nonlinear Finite Element Analysis and Instance of ABAQUS[M]. Beijing: Science Press,2005. |
| [6] | 汪召华,高莲士,宋文晶. 三维摩擦接触的有限元分析[J]. 清华大学学报:自然科学版,2002,42(增1):93-96. WANG Zhao-hua,GAO Lian-shi,SONG Wen-jing. Finite Element Analysis of 3-D Friction-contact Problems[J]. Journal of Tsinghua University: Science and Technology Edition,2002,42(S1): 93-96. |
| [7] | 石亦平,周玉蓉. 有限元分析实例详解[M]. 北京:机械工业出版社,2006. SHI Yi-ping,ZHOU Yu-rong. Finite Element Analysis Example Explanation[M]. Beijing: China Machine Press,2006. |
| [8] | 沈新普,王琛元,周琳. 一个钢筋混凝土损伤塑性本构模型及工程应用[J]. 工程力学,2007,24(9): 122-128. SHEN Xin-pu,WANG Chen-yuan,ZHOU Lin. A Damage Plastic Constitutive Model for Reinforced Concrete and Its Engineering Application[J]. Engineering Mechanics,2007,24(9): 122-128. |
| [9] | 聂建国,王宇航. ABAQUS 中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学,2013,30(4): 59-67. NIE Jian-guo,WANG Yu-hang. Comparison Study of Constitutive Model of Concrete in ABAQUS for Static Analysis of Structures[J]. Engineering Mechanics,2013,30(4):59-67. |
| [10] | Dassault Systems Simulia Corp. ABAQUS Documentation[M]. Ver. 6.11. Pawtucket,USA: ABAQUS Inc,2011. |
| [11] | Dassault Systems Simulia Corp. ABAQUS/CAE User's Manual[M]. Ver. 6.8. Pawtucket: ABAQUS,Inc,2008. |
| [12] | 李平,王家林. 预应力钢筋混凝土构件有限元模拟方法对比[J]. 重庆交通大学学报:自然科学版,2010,29(1): 27-29. LI Ping,WANG Jia-lin. Comparison of FEM Simulation Methods of Prestressed Reinforced Concrete Members[J]. Journal of Chongqing Jiaotong University:Natural Science Edition,2010,29(1): 27-29. |
| [13] | 王素裹,韩小雷,季静. ABAQUS显式分析方法在钢筋混凝土结构中的应用[J]. 科学技术与工程,2009,9(16): 4688-4692. WANG Su-guo,HAN Xiao-lei,JI Jing. Application of ABAQUS/Explicit in Reinforced Concrete Structures[J]. Science Technology and Engineering,2009,9(16):4688-4692. |
| [14] | 杨海旭,刘晚成. 无粘结预应力筋等效荷载的特性与应用[J]. 哈尔滨工业大学学报,2005,137(18): 1087-1089. YANG Hai-xu,LIU Wan-cheng. Characteristics and Applications of Equivalent Loads in Unbonded Prestressed Tendons[J]. Journal of Harbin Institute of Technology,2005,137(18): 1087-1089. |
| [15] | 薛伟辰. 现代预应力结构设计[M]. 北京: 中国建筑工业出版社,2003. XUE Wei-chen. Modern Prestressed Structure Design[M]. Beijing: China Building Industry Press,2003. |
| [16] | 徐伟炜,吕志涛,丁汉山. 无粘结智能预应力简支梁的力学性能研究[J]. 工程力学,2008,25(7): 142-146. XU Wei-wei,LV Zhi-tao,DING Han-shan. Study on Mechanical Behavior of Unbonded Smart Prestressed Beam[J]. Engineering Mechanics,2008,25(7): 142-146. |
| [17] | 胡成,方诗圣,吴文清. 预应力T梁反拱控制"挠度平衡法"的研究[J]. 合肥工业大学学报:自然科学版,1999,10(22): 42-47. HU Cheng,FANG Shi-sheng,WU Wen-qing. Research in "Deflection Balancing Method" for the Negative-arch Control of Prestressed Concrete T-beam. Journal of Hefei University of Technology: Natural Science Edition,1999,10(22): 42-47. |
 2014, Vol. 31
2014, Vol. 31
