扩展功能
文章信息
- 曾丁, 谢峻, 郑晓华, 任红伟, 王国亮
- ZENG Ding, XIE Jun, ZHENG Xiao-hua, REN Hong-wei, WANG Guo-liang
- 桥梁短期实测数据修正高强混凝土收缩徐变模型与长期挠度预测
- Prediction of Long-term Deflection and Correction of Shrinkage and Creep Model of High-strength Concrete of Bridge Based on Measured Short-term Data
- 公路交通科技, 2014, Vol. 31 (11): 72-77
- Journal of Highway and Transportation Research and Denelopment, 2014, Vol. 31 (11): 72-77
- 10.3969/j.issn.1002-0268.2014.11.012
-
文章历史
- 收稿日期:2013-12-10
收缩徐变是混凝土材料本身所固有的特性,简单地讲混凝土的收缩是指混凝土在硬化过程中,随时间增长而发生的体积改变,主要有自发收缩、干燥收缩、碳化收缩等。混凝土的徐变是指在长期荷载作用下,随时间增长发生的可恢复或不可恢复的附加变形。
经过几十年的试验研究与实践经验的积累,人们对混凝土收缩徐变的认识取得了很大进步,目前许多国家、组织提出的混凝土工程设计规范及理论,如英国的BS540规范﹑美国混凝土学会209委员会的ACI209建议﹑欧洲混凝土协会—国际预应力协会的CEB—FIP等都详细考虑了混凝土的收缩徐变效应。但各个国家和组织对混凝土收缩徐变机理的认识尚存在分歧,不仅计算模型繁简各异,且基本原理上也有不同,即经过多年的研究,混凝土的收缩徐变仍没有被人们充分认识和掌握。
造成上述局面的主要原因有两方面:(1)混凝土收缩与徐变是一个复杂的过程,影响因素很多,如混凝土的组成成分与配合比、结构几何尺寸、外加剂等内部因素及养护条件﹑环境温度、湿度等外部因素都影响混凝土的收缩徐变,之外,加载龄期、受力状态、应力水平﹑持荷时间也是影响混凝土徐变行为的因素;(2)绝大多数研究是在实验室特定环境下对小试件进行的,与实际混凝土结构物及所处环境差别较大。
相关科研人员除了对混凝土的收缩徐变进行实验室内标准试件的试验及理论研究之外,少数人员也进行了实际环境下的各种试验研究。一些研究者[1, 2, 3]通过试件短期试验建立了不同形式的混凝土长期徐变预测模型;有研究者[4, 5, 6, 7, 8]认为混凝土的徐变预测模型受材料本身及环境的影响,通过试件短期试验数据来修正预测模型,可以极大地提高预测模型的精度;也有研究者[9, 10, 11]通过配筋混凝土试件研究配筋对混凝土收缩徐变的影响,修正预测模型预测实桥的长期徐变变形。个别学者研究了循环荷载对高强混凝土徐变的影响[12]及混凝土收缩徐变的不确定性问题[13]。国际材料与结构研究实验联合会(RILEM)也推荐在重大工程中进行专门的徐变试验研究,通过短期试验修正收缩徐变模型,提高模型对长期收缩徐变预测的精度[14]。由于标准室内或现场的试件试验除了试验误差及环境影响之外仍与实际结构的应用存在着较大差异,如实际结构的受力状态﹑构造特点、尺寸效应等,导致其实际结构的收缩徐变参数与规范推荐模型有一定的差别。
本文针对当前混凝土梁桥收缩徐变估算方面存在的问题,通过在预应力混凝土梁桥上埋置测量不同应变的传感器元件,直接测量混凝土的收缩应变,按照运算理论[15]将恒载作用下的预应力混凝土的徐变应变分离出来,采用实桥短期实测数据修正具体桥梁的收缩徐变模型,并进行了验证及长期挠度的预测。
1 收缩徐变辨识系统简介如图 1所示,预应力混凝土梁桥收缩徐变辨识系统由测量系统﹑数据采集系统及数据处理系统三部分组成。
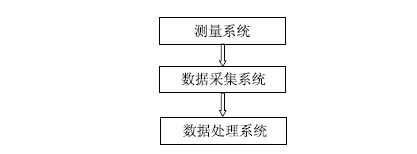
|
| 图 1 预应力混凝土梁桥收缩徐变辨识系统组成框图 Fig. 1 Block diagram of identification system of shrinkage and creep of prestressed concrete girder bridge |
应变测量系统由混凝土无应力测量及预应力混凝土应力测量两个子系统组成。其中无应力测量子系统主要由特制的夹层圆锥式无应力筒﹑含有温度测量的振弦式应变计及滑动材料三部分组成,用以测量混凝土的收缩应变。预应力混凝土应力测量子系统由一个或若干个含有温度测量的振弦式应变计组成,用以测量预应力混凝土的应变。
预应力箱梁顶底板埋置测量系统时,各传感器应位于同一水平面上,且纵桥向处于同一位置,筒外传感器与筒外壁应保持适当的间距。对于悬臂施工的预应力混凝土箱梁桥,测量系统一般应埋置在上部结构的合龙段内的顶﹑底板的适当位置。
数据采集系统由采集单元﹑控制单元及数据采集控制软件组成。数据采集单元必须与测量传感器配套。控制单元由计算机实现,其与数据采集控制软件一起实现数据的采集与控制。
数据处理系统由计算机﹑数据运算理论及软件部分组成。
此套系统的实施目的就是通过各类传感器的实测应变数据,经过科学运算自动分离预应力混凝土箱梁结构随时间变化的收缩应变与徐变应变。
2 收缩徐变模型的修正 2.1 应用桥梁简介及测点布置该研究实测工作位于之江大桥的东侧引桥上。如图 2所示,之江大桥东侧非通航引桥为双幅变截面三向预应力混凝土连续箱梁桥,主梁采用跨径(60+11×86+60)m一联形式,混凝土为C55高强混凝土。单幅断面形式为单箱双室斜腹板箱梁,箱梁顶板宽度18.55 m,底板宽9.0~10.256 m,两翼悬臂长3.75 m。桥面设置2.0%的向外单向横坡,由两侧腹板高差调整。混凝土箱梁根部断面梁高5.986 m,跨中和边跨现浇梁段梁高2.686 m,支点段外顶板厚28 cm;箱梁悬浇梁段至合拢段区间各梁段底板上、下缘按2.0次抛物线变化。下部结构采用现浇墩+矩形承台(或八边形承台)+钻孔灌注桩基础。
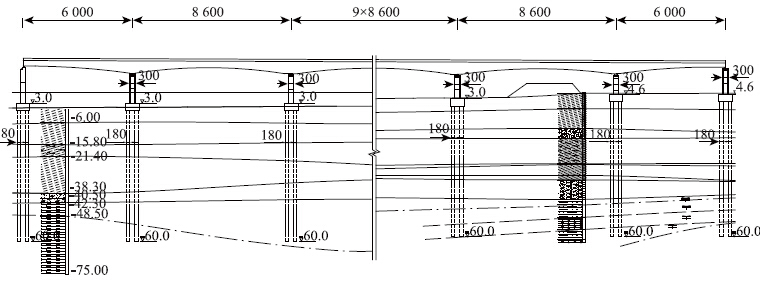
|
| 图 2 之江大桥东侧引桥桥型布置图(单位:cm) Fig. 2 Layout of eastern approach bridge of Zhijiang bridge(unit:cm) |
分别将两套测量系统埋置在右幅主桥侧起第三跨跨中合龙段的顶板和底板上,图 3是跨中截面测量系统埋置位置示意图,图 4是测量系统埋置照片。
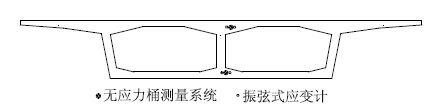
|
| 图 3 跨中截面传感器布置示意图 Fig. 3 Schematic diagram of layout of embedded sensors at mid-span |

|
| 图 4 测量传感器埋置照片 Fig. 4 Photo of embedded sensors |
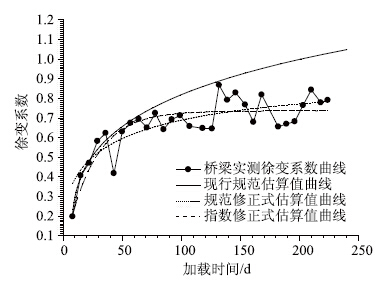
该桥箱梁短期实测混凝土收缩应变﹑现行规范收缩应变计算式及依据短期实测数据修正的收缩应变计算式估算曲线绘于图 5中,短期实测箱梁混凝土的徐变系数﹑现行规范徐变系数计算式及依据短期实测数据修正的徐变系数计算式估算曲线绘于图 6中。由图 5可知对于该桥箱梁C55混凝土,约25 d龄期内实测收缩应变小于现行规范的估算值,之后的实测收缩应变明显大于现行规范的估算值。由图 6可知加载初期(加载龄期约60 d)实测徐变系数与规范估算值相一致,之后徐变系数的实测值明显小于现行规范的估算值。即对于该桥上部结构使用现行规范的收缩徐变模型,总体上会低估C55高强混凝土的收缩作用,而高估徐变作用,这与文献[13]采用标准试件进行标准试验得到的结果一致。
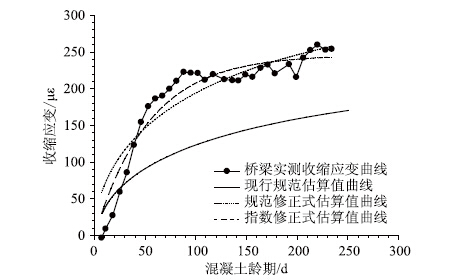
|
| 图 5 实桥混凝土收缩应变测量数据﹑理论值及拟合曲线 Fig. 5 Measured data,theoretical values and fitted curves of shrinkage strain of concrete of bridge |
|
| 图 6 实桥混凝土徐变系数测量数据﹑理论值及拟合曲线 Fig. 6 Measured data,theoretical values and fitted curves of creep coefficient of concrete of bridge |
现行规范中混凝土收缩应变计算式的修正式可以简化为:
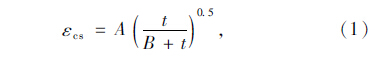
现行规范中混凝土徐变系数计算式的修正式可以简化为:
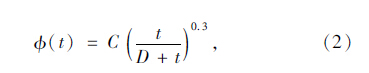
由之江大桥引桥连续箱梁短期实测收缩应变数据,按式(1)对现行规范收缩应变计算式修正后的收缩应变计算式:
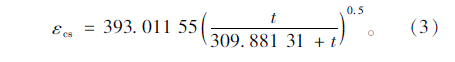
由之江大桥引桥连续箱梁短期实测徐变系数数据,按式(2)对现行规范徐变系数计算式修正后的徐变系数计算式是:
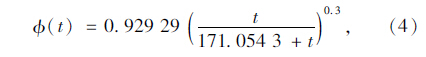
拟合参数A,B,C和D的标准差列于表 1中。
| 参数 | A | B | C | D |
| 标准差 | 72.161 79 | 164.650 07 | 0.088 27 | 89.661 8 |
由表 1可知拟合参数的标准差明显偏大,由图 5和图 6发现实测数据更接近于指数函数的分布形式。
对于高强混凝土文献[16]制作试件,进行收缩徐变试验,拟合得到指数函数徐变预测模型,通过实桥验证了该指数型收缩徐变模型比现有徐变模型具有更高的预测精度。因此,根据实测数据的变化趋势与指数函数较一致的情况,在此用下式表示混凝土的收缩应变发展规律:
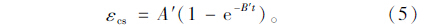
使用短期实测混凝土收缩应变数据对式(5)进行拟合得:
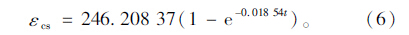
根据短期实测数据的变化趋势按指数函数:
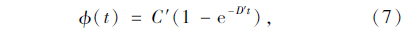
使用短期实测数据拟合的混凝土徐变系数发展规律为:
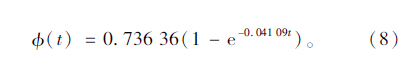
该桥预应力混凝土指数式收缩徐变模式拟合参数的标准差列于表 2中。
| 参数 | A′ | B′ | C′ | D′ |
| 均方差 | 7.150 16 | 0.001 80 | 0.017 4 | 0.005 27 |
比较表 1与表 2,可见依据实桥短期实测数据的混凝土收缩应变及徐变系数的两种拟合曲线中,指数函数模式的拟合参数的标准差远小于现行规范修正式的拟合参数的标准差。相对而言在图 5和图 6中,实测收缩应变及徐变系数与指数函数的拟合曲线吻合的更好一些。
3 修正模型的验证及跨中长期挠度预测
前文给出了根据实测短期数据拟合的两种形式混凝土收缩﹑徐变预测估算式,现在将其应用于恒载作用下的之江大桥东引桥(60+11×86+60) m 一联,通过跨中挠度实测数据对混凝土收缩徐变修正式进行验证及长期变形的预测。
按施工过程建立的之江大桥东引桥的有限元计算模型共由350个梁单元﹑553个节点﹑202个弹性连接元件组成,悬臂浇注节段施工分三个过程模拟,模拟施工计算由83个阶段组成。
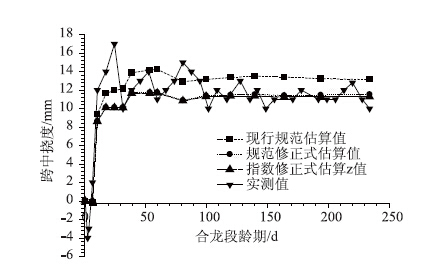
图 7是第三跨(埋置收缩﹑徐变辨识传感器的桥跨)跨中实测挠度与采用规范公式及依据实桥短期实测收缩徐变数据修正规范式﹑指数拟合收缩徐变模式的有限元计算结果的比较。由图可知该跨合龙后短期内理论预测结果与实测数据在趋势上基本一致,三种收缩﹑徐变模式的预测趋势也相一致,现行规范收缩徐变模式的估算值在后期明显偏高,而两个依据短期实测收缩徐变数据修正的收缩徐变模式的估算值与实测值吻合较好。特别是在短期内由实测数据修正规范式与指数拟合式的估算数据绘制的曲线基本一致。
|
| 图 7 短期实测跨中挠度与不同收缩徐变预测模型的理论计算跨中挠度 Fig. 7 Short-term measured deflection and calculated deflections of mid-span obtained by different shrinkage and creep prediction models |
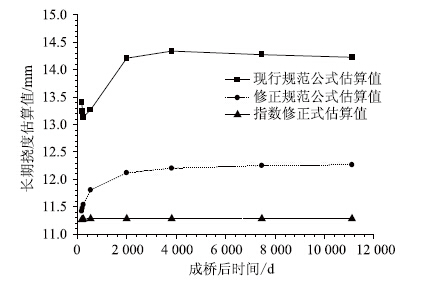
图 8是成桥后(铺装层完成)恒载作用下三种收缩﹑徐变模型的长期挠度预测结果示意图。现行规范收缩徐变模式对预埋传感器桥跨跨中的长期变形预测结果为:铺装层完成后,在大约1 a的时间内跨中挠度随时间的增加略有下挠,约在成桥后1~10 a 间跨中挠度又随时间的增加向上移动,成桥10 a 之后又随时间的增加缓慢地下挠。
修正规范式的预测结果为:在成桥后跨中以极小的速率一直在向上移动,30 a间跨中向上移动了0.845 mm。
指数拟合式的预测结果为:成桥后5 a之内随时间的增加跨中以极低的速率向上移动,5 a内向上移动了约0.022 mm;成桥5 a之后跨中又以极低的速率向下移动,25 a向下移动了约0.001 2 mm。
综合图 7和图 8可知,该桥在恒载作用下现行规范使用的收缩徐变模式对跨中的长期变形的估算偏大一些。
|
| 图 8 成桥后不同收缩徐变预测模型的长期理论计算跨中挠度 Fig. 8 Long-term deflections of mid-span after completion obtained by different shrinkage and creep prediction models |
(1)我国现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)的混凝土收缩与徐变计算模型是基于现行CEB-FIP模型结合我国的具体情况而建立的。混凝土收缩、徐变预测模型是大量实验室试件收缩、徐变试验数据拟合的结果,代表了标准试验条件下混凝土材料的共性,由于混凝土收缩徐变既受内因又受外因的影响,特别是具体到某一座桥梁其实际环境条件和桥梁的受力特征会明显影响到混凝土的时变性能,使用规范推荐模式估算桥梁在恒载作用下的长期变形可能会产生较大的偏差,因此,利用试件短期实测数据,特别是实桥短期实测数据修正已有收缩徐变模型来预测桥梁的长期变性是一种有效的方法。
(2)使用短期实测数据修正混凝土收缩徐变模式来预测桥梁恒载作用下的长期变形,其预测精度受实测数据的完整性﹑测量精度及修正式与实测数据的吻合程度的影响。
| [1] | 陈灿明,黄卫兰,陆采荣,等.桥用高性能混凝土的徐变与应用[J].水利水运工程学报,2007,2:1-9. CHEN Can-ming,HUANG Wei-lan,LU Cai-rong,et al. Creep of High-performance Concrete for Bridges and Its Application[J].Hydro-Science and Engineering,2007,2:1-9. |
| [2] | BROOKS J J,NEVILLE A M. Estimating Long-Term Creep and Shrinkage from Short-term Test[J]. |
| [3] | SIRVIVATNANON V. Predicting Long-Term Creep from Short-Term Creep Test[J]. ACI Special Publication,2005,229:49-62. |
| [4] | BAZANT Z P,PANULA L,KIM J K,et al.Improved Prediction Model for Time-dependent Deformations of Concrete:Part6—Simplified Code-type Formulation[J]. |
| [5] | BAZANT Z P,XI Yun-ping,BAWEJA S. Improved Prediction model for Time-dependent Deformations of Concrete: Part7—Short Form of BP-KX Model Statistics and Extrapolation of Short Time Data[J]. |
| [6] | 许航,彭小明,邹立群. 基于短期试验的桥梁混凝土长期徐变预测研究[J].重庆交通大学学报:自然科学版,2010,29(4):518-520.XU Hang,PENG Xiao-ming,ZOU Li-qun. Prediction Research of Long-term Creep for Bridge Concrete Based on Short-term Test[J].Journal of Chongqing Jiaotong University: Natural Science Edition,2010,29(4):518-520. |
| [7] | OJDROVIC R P,ZARGHAMEE M S. Concrete Creep and Shrinkage Prediction from Short-term Tests[J].ACI Materials Journal,1996,93(2):169-177. |
| [8] | 王辉,钱春香. 基于苏通大桥混凝土短期试验结果的徐变预测模型修正[J].桥梁建设,2010[DK] (2):32-36. WANG Hui,QIAN Chun-xiang. Modification of Creep Prediction Models Based on Short-term Concrete Test Data of Sutong Bridge[J]. Bridge Construction,2010(2):32-36. |
| [9] | 孟少平,潘钻峰,王辉,等.苏通大桥辅桥高性能混凝土收缩和徐变试验及分析[J].现代交通技术,2009,6(5):15-20.MENG Shao-ping,PAN Zuan-feng,WANG Hui,et al. Creep and Shrinkage Experiments and Analysis on High-performance Concrete of Sutong Bridge[J]. Modern Transportation Technology,2009,6(5):15-20. |
| [10] | 张运涛,孟少平,惠卓,等.苏通大桥连续刚构桥主梁混凝土徐变试验研究[J].公路交通科技,2010,27(4):101-104.ZHANG Yun-tao,MENG Shao-ping,HUI Zhuo,et al. Experimental Research on Concrete Creep for Main Girder of Continuous Rigid Frame Bridge of Sutong Bridge[J]. Journal of Highway and Transportation Research and Development,2010,27(4):101-104. |
| [11] | 张运涛,孟少平,惠卓.配筋高性能混凝土收缩徐变试验研究[J].建筑科学,2010,26(3):1-5.ZHANG Yun-tao,MENG Shao-ping,HUI Zhuo. Experimental Study on Creep and Shrinkage of High-performance Reinforced Concrete[J]. Building Science,2010,26(3):1-5. |
| [12] | 赵启林,陈立,翟可为,等.复杂状态下桥用高强混凝土收缩徐变性能试验[J]. 解放军理工大学学报:自然科学版,2011,12(5):459-465.ZHAO Qi-lin,CHEN li,ZHAI Ke-wei,et al. Creep and Shrinkage of High Strength Concrete for Bridges under Complex Condition[J].Journal of PLA University of Science and Technology: Natural Science Edition,2011,12(5):459-465. |
| [13] | 潘钻峰,吕志涛,刘钊,等.苏通大桥连续刚构收缩徐变效应的不确定性分析[J].工程力学,2009,26(9):67-73.PAN Zuan-feng,LV Zhi-tao,LIU Zhao,et al. Uncertainty Analysis of Creep and Shrinkage Effect in Continuous Rigid Frame of Sutong Bridge[J]. Engineering Mechanics,2009,26(9):67-73. |
| [14] | RILEM Technical Committees. Guidelines for Characterizing Concrete Creep and Shrinkage in Structural Design Codes or Recommendations[J]. |
| [15] | 谢峻,曾丁,郑晓华.基于收缩徐变自辨识的大跨径梁桥长期挠度预测[J].公路交通科技,2013,30(8):88-91.XIE Jun,ZENG Ding,ZHENG Xiao-hua. Long-term Deflection Prediction of Long-span Beam Bridge Based on Shrinkage Creep Self-identification[J].Journal of Highway and Transportation Research and Development,2013,30(8):88-91. |
| [16] | 柯敏勇,刘海祥,陈灿明,等. 高强混凝土指数型收缩徐变预测模型及工程应用[J].桥梁建设,2011(4):49-52.KE Min-yong,LIU Hai-xiang,CHEN Can-ming,et al.Prediction Model of Index Type Shrinkage and Creep for High-Strength Concrete and Its Engineering Application[J].Bridge Construction,2011(4):49-52. |
 2014, Vol. 31
2014, Vol. 31
