扩展功能
文章信息
- 胡骥, 胡万欣, 蒋晶尧
- HU Ji, HU Wan-xin, JIANG Jing-yao
- 放松规制下的出租车服务定价博弈模型
- Game Model of Taxi Service Pricing Based on Deregulation
- 公路交通科技, 2014, 31(10): 148-153
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 148-153
- 10.3969/j.issn.1002-0268.2014.10.024
-
文章历史
- 收稿日期:2013-9-11
2. 武汉铁路职业技术学院, 湖北 武汉 430205;
3. 玉林市城乡规划设计院, 广西 玉林 537000
2. Wuhan Railway Vocational College of Technology, Wuhan Hubei 430205, China;
3. Yulin Urban and Rural Planning & Design Institute, Yulin Guangxi 537000, China
随着经济的发展和人们出行结构的变化,出租车已成为城市公共交通系统的重要组成部分。其中,出租车行业的经济规制问题受到普遍关注,不同程度地放松或解除对它的经济规制成为可能的趋势。目前我国出租车行业处于严格规制的状态,已出现许多规制失灵的现象,如行业利润在出租车经营企业和出租车司机之间的畸形分配,消费者与经营者间的供需矛盾等[1]。出租车运价是分配客运资源和协调行业参与者利益需求的重要手段,也是近年来各方研究的焦点。Douglas[2]分析了乘客平均候车时间与出租车空载率的反比关系,提出了出租车市场需求量与平均出行费用和平均等车时间的集合模型。Cairns等[3]指出了出租车服务的价格规制对产生均衡的重要性,认为次优定价只有在出行费用和出租车使用强制管制下才能实现。Chang[4]建立了灵活起步价的随机最优控制模型,在一定程度上降低了空载率。王俊等[5]对出租车定价形式进行了分析,得出应按社会福利最大化的定价原则来制订费用。杨海[6]探讨了不同出租车市场结构运营条件和出租车静态市场的平衡机制。陈茜等[7]通过分析出租车供需关系,提出了总量控制下出租车价格及相关费用制订的推算方法。杨忠振等[8]使用Logit型PSM函数建立了具有竞争力的租价体系下的市场规模模型,得到了出租车两公里内的起步价。郭晶伟[9]分析了出租车、公交车、地铁三种交通方式的实际效能,计算了三种交通方式的效能价格比及推荐范围值。周和平等[10]综合考虑驾驶员与出行者利益,以出行者时间费用成本最小为目标函数,构建了出租车合乘路径选择与费率优化模型。劳潮惠等[11]从数量、价格、服务和行为四个方面探讨了政府规制体系,但并未提出具体合适的价格制订方法。慕晨等[12]用多Agent技术研究了城市出租车运营系统定价问题,设定了分担率线性加权的价格优化目标,并运用仿真优化方法求解。以上研究都没有考虑在规制过程中如何制订出租车价格的问题。鉴于此,本文使用经济学的方法,从社会福利和行业成本等角度对我国城市出租车行业规制进行研究,通过分析价格规制过程中政府与出租车公司的博弈关系,建立价格规制博弈模型,从而为政府对出租车行业的规制决策提供理论依据,为出租车行业的改革提供一定的思路和方法。 1 放松规制条件下价格模型的基本设定 1.1 问题描述
考虑到我国出租车行业的发展现状和不充分的行业市场竞争条件,结合其他国家的规制发展经验,可以发现实行价格上限的规制(即规制者针对本地区的出租车价格设定一个上限,行业经营者可以在这一上限下自由定价,这样既允许一定程度的价格竞争,又可以保护消费者利益并提升社会福利)是当前我国出租车行业可以选择的一种定价模式。在出租车行业规制中,政府的目标是社会福利最大化,出租车公司的目标是自身收益最大化。政府对出租车通过一些价格管制手段(决策变量)来进行规制,以规范出租车行业。 1.2 模型基本假设
通过分析,可以认为政府与出租车公司之间存在主从决策关系的斯坦克尔伯格博弈。两者间的博弈关系可以描述为:规制者(政府)首先采取行动,实施相应的规制手段(价格规制手段);出租车公司后行动,依据规制者(政府)的行动调整企业的营运策略。同时认为出租车公司与出租车司机都是为乘客服务,可忽略二者之间的内部利益分配矛盾,将两者利润收益统一考虑。
假定政府对出租车行业的规制手段为政府通过财政税收对出租车行业按营运里程q进行补贴,设每营运公里费用为m(即决策变量为m),相应的转移支付为mq。
根据经济学的相关理论,在出租车行业供需均衡且考虑转移支付及影子成本时,消费者(乘客剩余)效用U(q)可以表示为:
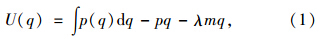
依据微观经济学成本为凸函数,假设出租车公司的成本为:

出租车公司的利润表示为:
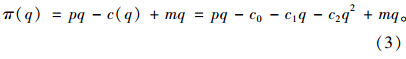
政府规制的目标函数为:
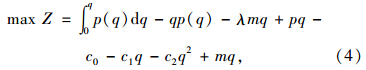
出租车公司目标函数为:
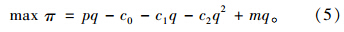
政府与出租车公司之间的博弈分为两个阶段。阶段一:规制者调整决策变量m以实现社会福利最大;阶段二:出租车公司采取行动,改变自身运营方案(运营里程q)实现出租车公司利润最大化。政府在出租车公司利润最大化的基础上考虑社会福利最大化做出最优决策,这一过程可用双层规划形式来描述,政府与出租车公司之间的博弈用数学模型表示如下:
上层规划(U1):
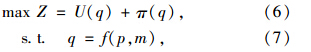
下层规划(L1):
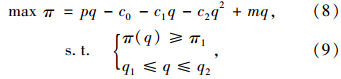
2 考虑出租车实载里程的博弈模型分析
上述模型为出租车价格规制的基本模型,在现实行业运行模式中,有诸多因素影响出租车的行业价格,其中实载里程是最重要的因素之一,本文就以此来建立模型。在现实模式中,出租车在实载和空载两种状态间变换,假设需求函数与出租车的实载里程和空载里程相关,乘客的需求函数Qi=f(p,k),式中,p为单位运营里程的服务价格;k为出租车实载率,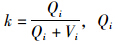 为出租车实载里程数,Vi为出租车空载里程数。
为出租车实载里程数,Vi为出租车空载里程数。
依据经济学原理,乘客的需求函数可表示为:

乘客的逆需求函数为:

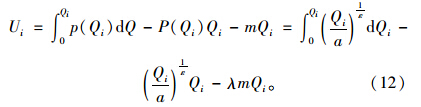
乘客效用总和为:
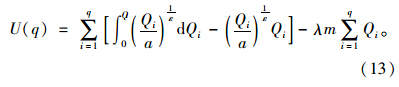
考虑实载里程和空载里程,单辆出租车的成本可以表示为:
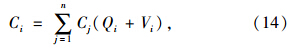
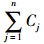 为出租车每营运公里的平均成本;n为不同的成本构成数目。
为出租车每营运公里的平均成本;n为不同的成本构成数目。出租车公司的营运总成本可以表示为:
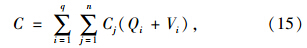
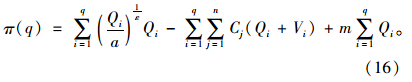
政府最优规制的目标函数可以表示为:
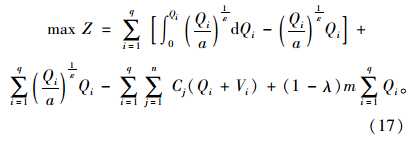
政府与出租车公司之间存在主从博弈。假定政府在保证社会福利最大化的基础上考虑出租车公司利润最大化做出最优决策,政府与出租车公司之间的博弈可用数学模型表示如下:
上层规划(U1):为式(17),
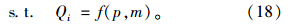
下层规划(L1):
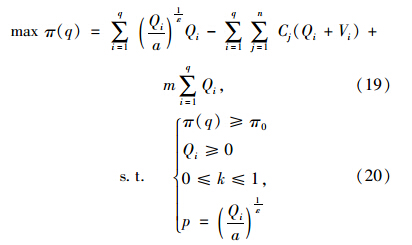
3 模型求解
前文建立的模型可以采用遗传算法求解,遗传算法的基本思路是:
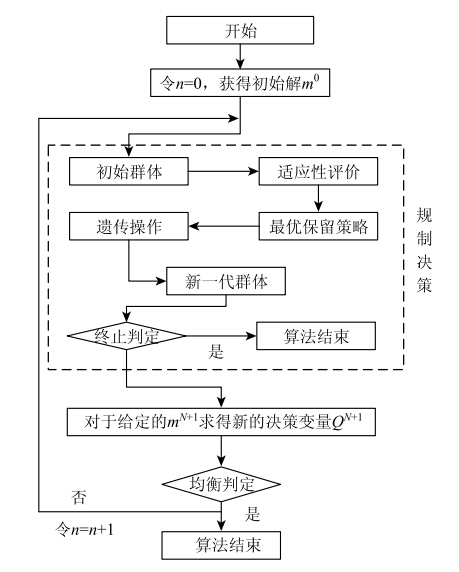
(1)上层采用多目标遗传算法,提供一个有效的解集;(2)按照偏好对解排序;(3)把上层规划所得到的解传递给下层规划;(4)下层规划采用相关算法,逐步靠近上层规划的满意可行解;(5)上层规划依据偏好最终取得双层规划的满意可行解。具体设计思路见图 1。
|
| 图 1 遗传算法设计思路 Fig. 1 Route for designing genetic algorithm |
对于上述模型进行遗传算法的初步设计:
(1)编码。此过程是算法设计过程的第一步,许多情况下以二进制形式进行编码。
(2)适应值函数的定义。适应值函数关系到种群的进化,在算法流程中适应值为非负,对于算法来说适应值越大越好。
(3)控制参数确定。杂交概率pc:pc越高,种群中引入的速度越快,但丢失已获得优良基因的速度也会相应提高,pc变低,则可能使搜索遇到障碍,一般取pc=0.4~0.99。群体规模n:n大时,会增加计算难度;n小时,搜索空间受限,可能出现未收敛的情况。专家建议n=20~200。变异概率pm:为了使种群稳定,个体变异后不会与父代产生过大的差异,pm取值要小,一般情况下pm=0.001~0.1。
(4)产生初始群体。一般为随机产生初始群体。产生的个体需要检查是否满足约束,不满足需要则重新生成初始种群。
(5)遗传操作。①选择。从父代中选取适应值较大的几个个体,让其不参与遗传操作,用来取代下一代适应值较小的几个个体。在剩下的个体中将适应值较大的遗传到子代。②杂交。将父代的优良基因传给下一代,并生成包含更复杂基因的新个体。③变异。对于每次产生的子代,以一定的pm进行变异。
(6)算法终止判定。当群体进化处于稳定状态时,结束群体进化过程。
依据上述遗传算法设计求解模型的具体算法步骤为:
第0步:
(1)确定上层目标函数Z到个体适应度转换规则
适应度函数G(m)为:
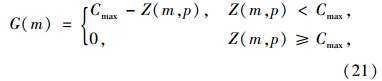
(2)确定个体进行选择规则[13]
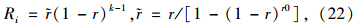
第一步:指定出租车定价策略的上、下限p0,pp,随机产生一个初始定价的原始群体(确定一组初始价格解集P(k)=(p1,p2,…,pk)),设置进化代数计数器,令n=0,最大迭代步数为MaxIter。
第二步:将上层规划的目标函数转化为式(19)中的适应度函数G(m),对G(m)的约束条件用罚函数法处理。
第三步:对每个个体解码,用P(k)n计算上层问题U1的目标函数值Z(P(k)n),将P(k)n代入下层问题L1并对其求解,求得对应的不同规制信息下的m,进而求解上层目标函数值p,得到各个个体的适应度值。
第四步:根据个体适应度值和式(20)对个体进行选择,从P(n)中选择优良的个体,复制到下一代群体P(n+1)中,然后按照杂交概率pc交换它们的部分染色体,最后得到个体变异概率pm并产生新的个体。
第五步:如果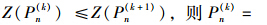
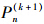 ,令n=n+1,转至第3步。
,令n=n+1,转至第3步。
第六步:当n=MaxIter时,即满足终止条件,则算法结束,否则转至第5步。
第七步:输出最优解结果。 4 算例分析
下面进行简单的算例分析,算例选取的基础数据为某市的实际调查数据,如表 1、表 2所示。
| 日均营运天数/d | 日均营运时间/h | 日均运营里程/km | 日均载客里程/km | 日均载客率/% |
| 28 | 18 | 342.66 | 237.61 | 69.34 |
| 成本类型 | 成本构成 | 成本费用/(元·月-1) |
| 直接成本 | 车辆折旧费、燃料费、车辆规费、车辆维修费、车辆保险费、智能管理系统服务费、事故损失费、司机社会保险费和其他 | 10 608.94 |
| 间接成本 | 管理人员的工资、车辆牌照经营权使用费分摊、办公费、水电费、招待费、低值易耗品、租赁费、通讯费、会议费、广告费、无形资产和长期资产摊销、保险费、其他管理费用 | 2 764.98 |
计算模型所需的相应值如下。
单位车辆运营成本:10 608.94+2 764.98=13 373.92元/月。
单位里程运营成本:13 373.92/(28×237.61)=2.01元/km
价格弹性系数ε:依据相关文献可知一般情况为1.0~1.4,此处取中间值1.25。
影子成本λ:一般取值为1.1~1.5,这里取1.25。
因此,可得相应所需数据如表 3所示。
| 空载率/% | 单位里程运营成本/(元·km-1) | 价格弹性系数 | 影子成本 | 出租车总量/veh |
| 30.66 | 2.01 | 1.2 | 1.25 | 18 858 |
对于算法做如下设定:
(1)模型中编码形式为二进制,采用最优存储策略与轮盘赌方式相结合的方式使算法收敛;(2)群体规模n=50,杂交概率pc=0.5,变异概率pm=0.005;(3)模型交叉形式选择为双点交叉,交叉每次选取两个父代,以0.5的概率进行杂交;(4)算法随机生成60个初始个体,检查是否能满足模型对应的约束,如不能满足约束条件,则需返回重新生成初始群体。
依据遗传算法求得出租车单位服务价格p为2.51,即单位里程平均运价为2.51元/km。
通过上述分析计算,可得单位里程平均运价为2.51元/km时,能够实现政府社会福利最大化和出租车公司自身利益最大化的规制目标,从而达到一个稳定的均衡状态。分析模型可知,影响出租车价格的因素除了市场因素外,政府通过适当措施(增加补贴、引入竞争)调节价格,亦可使出行者与出租车公司的效益最大化。调查可知,2009年至2010年间,该市出租车的实际平均运价约为2.66元/km,出行者满意度为80%。在模型计算时如果加大财政补贴,引入市场竞争,所得的价格与政府严格规制下的价格相比会有所下降,同时有利于在出租车行业发挥价格机制,增加社会福利。
通过算例,对放松规制定价博弈模型进行了研究,计算结果能够有效地反应定价过程,表明该模型与算法是有效的。同时,政府可以调整财政补贴,增减出租车投放量,引入竞争发挥价格机制来提高出行者满意度,同时提高社会福利。
5 模型推广
在放松规制的条件下考虑时间因素,价格规制是一个长期动态的过程。本文研究[0,t]时间内政府与出租车公司的连续动态决策。可以建立一个价格规制的动态博弈模型,政府通过对决策变量m的动态控制,达到对价格的动态规制,为出租车行业放松规制提供借鉴。鉴于此,可以把出租车实载里程的价格规制模型推广为如下情况:
上层规划(U1):
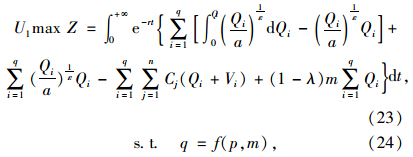
下层规划(L1):
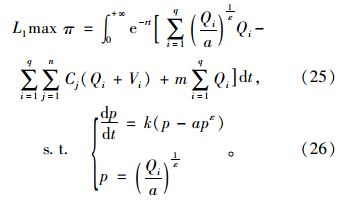
鉴于我国出租车行业发展现状和不充分的行业市场竞争条件,政府采取合理的价格规制手段,允许一定程度的价格竞争,可以保护消费者不受价格欺诈并提升社会福利。目前我国出租车行业规制过于严格,出租车行业管理未来发展的方向是放松规制。通过基于双层规划理论得到的规制价格分析结果,采取设定的规制价格是一种可行的手段,可以为政府制订政策提供借鉴,具有实际意义。对于政府价格规制来说,是一个长期的动态过程,文中只是对单一静态的价格规制问题进行了讨论,对于动态价格规制并未做深入探讨,这也是以后研究方向之一。
| [1] | 周璨.出租车市场政府管制问题研究[D].重庆:西南政法大学,2010. ZHOU Can. Governmental Regulation on Taxi Market[D].Chongqing: Southwest University of Political Science and Law,2010. |
| [2] | DOUGLAS G W. Price Regulation and Optimal Service Standards: The Taxicab Industry[J]. Journal of Transport Economics and Policy, 1972, 6(2): 116-127. |
| [3] | CAIRNS R D, LISTON-HEYES C. Competition and Regulation in the Taxi Industry[J]. |
| [4] | CHANG T H, CHU T S. Optimal Taxi Market Control Operated with a Flexible Initial Fare Policy[C]//2004 IEEE International Conference on Networking, Sensing and Control. [s. l.] : IEEE, 2004: 1335-1340. |
| [5] | 王俊,陈学武.用经济学理论分析出租汽车服务定价机制[J].交通运输工程与信息学报,2004,2(4): 99-104. WANG Jun,CHEN Xue-wu. Analyzing the Pricing Mechanism of the Taxi Service with Economics Theory[J]. Journal of Transportation Engineering and Information, 2004,2 (4): 99-104. |
| [6] | YANG H, YE M, TANG W H, et al. Regulating Taxi Services in the Presence of Congestion Externality [J]. Transportation Research Part A, 2005, 39(1): 17-40. |
| [7] | 陈茜,王炜,黄娟.需求控制下的出租车计程定价问题研究[J] .城市交通,2005,3(3):14-18. CHEN Qian, WANG Wei, HUANG Juan. The Study of Distance-accounting Taxi Price under Demand Control [J]. Urban Transport of China, 2005,3(3):14-18. |
| [8] | 杨忠振,王璐.城市客运出租车起步价格模型分析[J].大连海事大学学报,2006,32(1):38-41. YANG Zhong-zhen, WANG Lu. Model Analysis of the Taxi Starting Price in a City[J]. Journal of Dalian Maritime University, 2006,32(1):38-41. |
| [9] | 郭晶伟,马兰,过秀成, 等. 基于效能价格的出租车合理比价研究[J]. 交通标准化,2009(2): 52-57. GUO Jing-wei,MA Lan,GUO Xiu-cheng, et al. Reasonable Price Ratio of Taxi Based on Efficiency Price[J]. Transportation Standardization, 2009 (2): 52-57. |
| [10] | 周和平,钟璧樯,彭霞花,等.出租车合乘路径选择与费率优化模型[J].长沙理工大学学报:自然科学版),2011,8(1):20-24. ZHOU He-ping, ZHONG Bi-qiang, PENG Xia-hua,et al. The Route Choice and Rate Optimization Model of Taxi-pooling[J]. Journal of Changsha University of Science and Technology: Natural Science Edition, 2011,8(1):20-24. |
| [11] | 劳潮惠,吴群琪.城市出租客运行业特性与政府规制分析[J].公路交通科技,2013,30(6):132-135. LAO Chao-hui,WU Qun-qi. Analysis on Characteristics and Government Regulation of Taxi Industry[J].Journal of Highway and Transportation Research and Development, 2013,30(6):132-135. |
| [12] | 慕晨,赵祥模.基于多主体技术的出租车定价仿真优化方法[J].电子测试, 2013(13):39-42. MU Chen,ZHAO Xiang-mo. Agent Based Simulation Methods of Pricing Taxi Operation System[J].Electronic Test, 2013(13):39-42. |
| [13] | 肖剑,但斌,张旭梅.供货商选择的双层规划模型及遗传算法求解[J]. 重庆大学学报:自然科学版,2007,30(6):155-158. XIAO Jian, DAN Bin, ZHANG Xu-mei. Bi-level Programming Model and Genetic Algorithms for the Selection of Vendors[J]. Journal of Chongqing University: Natural Science Edition, 2007,30(6):155-158. |
 2014, Vol. 31
2014, Vol. 31
