扩展功能
文章信息
- 税文兵, 何保红, 何民
- SHUI Wen-bing, HE Bao-hong, HE Min
- 连续需求下整合关税成本的选址-库存模型
- A Location-inventory Model Integrating Duty Cost with Sequential Demand
- 公路交通科技, 2014, 31(10): 141-147
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 141-147
- 10.3969/j.issn.1002-0268.2014.10.023
-
文章历史
- 收稿日期:2013-8-26
随着经济的全球化和我国实施走出去的发展战略,越来越多的企业开始走向国际化发展道路,纷纷在技术人才密集的地区设立研发机构,在成本较低的地区建立生产基地,在资源丰富的地区选择供应商,在主要的顾客区设立配送中心。因此,全球供应链管理就成了企业走向国际化发展道路必须面对的挑战。和单一国家范围内的供应链管理相同,物流网络设计仍然是全球供应链管理战略层次的决策问题,对企业跨国经营绩效有着重大的影响。然而,由于全球供应链跨越了国家界限,涉及到关税、汇率等传统供应链没有的因素,使得全球供应链网络设计变得更加复杂。
由于关税对全球供应链的利润有重要影响,所以对国际物流网络设计的研究大多考虑了关税成本。Arntzen[1]以某公司的全球供应链为背景,从如何利用关税退税来降低关税成本的角度,建立了多周期、多产品、多层级和多运输方式的国际物流网络设计模型,并对设施的位置、生产、运输和库存量进行决策。虽然所建立的模型考虑了三种形式的关税退税,却没有将正常关税包含在目标函数中,因此对关税影响的考虑是不全面的。另外,该模型对库存成本的计算是基于需求瞬时发生的假设,因此其应用有一定的限制。Ricardo[2]针对由原材料供应商、工厂、配送中心和需求点构成的全球供应链,建立了单周期、多产品、四层级的国际物流网络设计模型。模型考虑了配送中心的增值税、从供应商到成品工厂的关税退税和工厂的库存持有成本,同时对配送中心是否打开、产品的生产位置、层级之间的运输量进行决策。模型虽然考虑了部分节点的增值税和关税退税,但作为计算基础的产品价值被假定为已知参数,没有与产品在供应链中的价值增值过程联系起来。而在供应链网络确定前,产品的价值是很难确定的。另外,该模型在计算库存成本时,假定平均库存天数是已知的,没有与平均库存量同步优化。Tsiakis[3]针对由工厂、配送中心和顾客构成的三级全球供应链,将关税的计算与产品在供应链中的价值增值过程联系起来,建立了多产品、三层级的国际物流网络设计模型。模型明确考虑了产品的关税,同时对设施是否建立、设施之间的分配关系、配送中心与顾客的分配关系、工厂的产量以及层级之间的运输量进行决策,基于产品在供应链中的价值增值过程来计算关税,体现了供应链网络结构对关税的影响。然而,模型在计算从配送中心到顾客的关税时,忽略了产品从工厂到配送中心的价值增值。Bassett[4]针对由原材料供应商、工厂和顾客构成的三级全球供应链,建立了单产品、多周期、三层级的国际物流网络设计模型。模型考虑了关税成本、工厂和顾客的库存持有成本,同时对工厂是否建立、工厂和顾客的库存量、产品的生产和销售路径进行决策。由于模型设立了产品从原材料到成品再到顾客手中路径的跟踪变量,因此能够精确地反映产品在供应链中的价值增值过程并合理地计算关税。然而,跟踪变量的引入大大增加了模型的复杂程度,对模型的求解带来一定困难。
除了考虑关税成本的国际物流网络设计外,另外一些学者研究了考虑汇率波动的国际物流网络设计。Huchzermeier[5]针对由供应商、工厂和市场构成的全球供应链,建立了考虑汇率波动的单产品、单周期、三层级的国际物流网络设计模型。模型以工厂所在国的货币为基准,对供应商和市场所占国的货币进行转换,同时对工厂是否打开、层级之间是否建立供应关系和层级之间的运输量进行决策。Das[6]针对配送中心和顾客在同一个国家的全球供应链,分别建立了战略层面的供应链网络设计模型和运营层面的库存控制模型,对网络结构变量和库存控制参数进行决策。然而,论文采用先选址再库存的传统方法,没有考虑选址与库存之间的影响关系。
从上述文献可以看出,对国际物流网络设计的研究无论是考虑关税成本还是汇率波动,都是基于传统的设施选址模型或动态选址模型,忽视了连续需求下库存成本的影响。一方面,国际物流具有地理范围大、运输距离长的特点,为了满足顾客的需求往往需要保管更多的库存;另一方面,基于选址与库存的相互影响,理论和实践都已经证明在设施选址模型中考虑库存成本的重要性。Baumol[7]首先提出应该在选址模型的目标函数中包含库存成本。McCann等[8]建立了确定环境下基于经济订货批量的连续选址-库存模型。Nozick[9]等研究了连续(S-1,S)补货策略下的选址-库存模型。Shen[10]、Snyder[11]、唐凯[12]、税文兵[13]等从不同的角度研究了(Q,R)库存策略下的选址-库存模型。然而,这些模型都只考虑了单一国家物流环境,缺乏对关税、汇率等国际因素的考虑,还不能用于国际物流网络设计。
本文针对现有研究的不足,以原材料供应商、工厂、配送中心和需求点构成的四层级全球供应链为对象,基于产品在供应链中的价值增值过程计算各节点的关税成本,利用梯级库存持有成本概念,建立连续需求下整合关税成本的多层级选址-库存模型。模型以选址成本、库存成本、运输成本和关税成本最小为目标,实现多种成本的平衡,弥补现有研究仅限于需求瞬时发生的情况。由于所建立的模型较为复杂,常规的算法难以在有限时间内求解,因此,设计了基于粒子群优化的智能优化算法,通过多个算例,验证模型的有效性和算法的可行性。 1 建立模型
本文所研究的供应链由分布在不同国家或地区的供应商、工厂、配送中心和顾客构成。供应商向工厂提供原材料,工厂根据配送中心的订单进行生产,产品生产出来之后通过配送中心运往顾客。配送中心通过成品库存满足若干顾客的确定需求,工厂分别通过原材料库存和成品库存满足生产和配送中心的需要。原材料运往工厂时,需要向工厂所在国上缴进口关税,同样产品运往配送中心和顾客时,需要向所在国上缴进口关税。 1.1 模型符号
(1)符号参数
I为顾客的集合;i为某位顾客;J为配送中心的集合; j为某个配送中心;P为工厂的集合;p为某个工厂;S为供应商的集合;s为某个配送中心;di为顾客的需求(单位/a);DDj为配送中心的需求(单位/a);DMp和DPp分别为工厂原材料仓库和成品仓库的需求(单位/a);FDj,ODj,HDj,EDj,DHj分别为配送中心的打开成本(元/a)、订货成本(元/次)、库存持有成本(元/单位)、梯级库存持有成本(元/单位)、单位成品平均库存成本(元/单位);FPp,OPp,OMp,HPp,HMp,EPp,EMp,MPp,MHp,PHp分别为工厂的打开成本(元/a)、成品订货成本(元/次)、原材料订货成本(元/次)、成品库存持有成本(元/单位)、原材料库存持有成本(元/单位)、成品梯级库存持有成本(元/单位)、原材料梯级库存持有成本(元/单位)、单位产品生产成本(元/单位)、单位原材料平均库存成本(元/单位)、单位成品平均库存成本(元/单位); FSs,PSs分别为供应商的选择成本(元/a)、单位原材料售价(元/单位); TSsp,TPpj,TDji分别为供应商到工厂、工厂到配送中心以及配送中心到顾客的单位运输成本(元/单位); RSsp,RPpj分别为供应商s到工厂p和工厂p到配送中心j的运输比例;adssp,adppj,addjc分别为供应商到工厂、工厂到配送中心以及配送中心到顾客的进口关税税率;DCSsp,DCPpj,DCDjc分别为供应商到工厂、工厂到配送中心以及配送中心到顾客的单位关税成本(元/单位);BOM为成品和原材料之间的数量关系;B为大的正数。
(2)决策变量
XDj为配送中心是否打开的二元变量,如果打开取1,否则取0;XPp为工厂是否打开的二元变量,如果打开取1,否则取0;XSs为供应商是否被选用的二元变量,如果被选用取1,否则取0;YDji为配送中心和顾客之间是否建立运输关系的变量,如果建立服务关系取1,否则取0;YPpj为工厂和配送中心之间是否建立运输关系的变量,如果建立服务关系取1,否则取0;YSsp为供应商和工厂之间是否建立服务关系的二元变量,如果建立服务关系取1,否则取0;QPpj为工厂到配送中心的运输量(单位/a);QSsp为供应商到工厂的运输量(单位/a);OQDj为配送中心订货批量(单位/次);OQMp为工厂原材料订货批量(单位/次);OQPp为工厂成品订货批量(单位/次)。 1.2 单位产品关税的计算
进口关税以产品的价值为征收基础[14],因此,计算产品的关税时,产品的价值必须得到正确的反映。原材料从供应商运输到工厂时,产品的价值包括原材料的采购成本和运输成本。单位产品的关税计算如下:
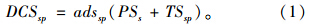
产品从工厂运往配送中心时,产品的价值增值部分包括生产成品、工厂的平均库存成本和运输成本,因此,单位产品的关税计算如下:
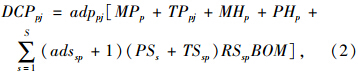
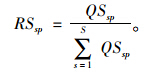
产品从配送中心运往顾客时,产品的价值增值部分包括配送中心的平均库存成本和运往顾客的运输成本,单位产品的关税计算如下:
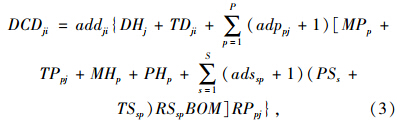
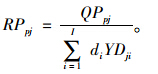
式(2)和式(3)中,平均库存成本等于总的库存成本除以处理量,其计算表达式如下:
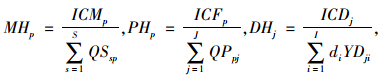
基于梯级库存持有成本概念,可以得到配送中心和工厂的库存持有成本。在此基础上融合设施的打开成本、运输成本、生产成本和关税成本,考虑各种约束条件,形成如下的选址-库存模型。
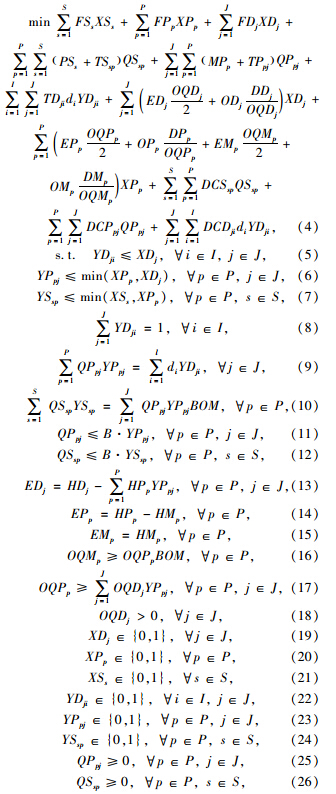
所建立的模型属于混合整数非线性规划模型,同时也是典型的NP困难问题。传统的精确算法难以在有限的时间求解较大规模的问题,因此,本文采用智能优化算法求解。在众多的智能优化算法中,鉴于粒子群优化(Particle Swarm Optimization,PSO)算法具有简单、易于实现、没有过多的参数需要调整等优点[15],本文选择PSO算法求解所建立的模型。 2.1 粒子群初始化
粒子群初始化包括粒子的编码和粒子群的生成。通过对模型的分析发现:一旦供应商的选择、工厂和配送中心的打开变量取值确定后,可以通过求解最小成本网络流问题和EOQ模型得到运输量和订货批量。因此,本文采用局部二进制编码策略,即仅对决策变量中的节点位置变量进行编码。在上述编码规则下,每个粒子的长度为候选供应商、工厂和配送中心的数量之和,粒子群采用随机的方法生成。 2.2 适应度函数的确定
适应度函数由四部分组成。第一部分为根据每个粒子计算得到的选址成本LocaC;第二部分为总的运输成本TrafficC。该运输成本通过最小费用增广路径算法[16]求解如下的最小成本网络流问题得到:
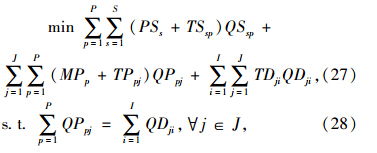
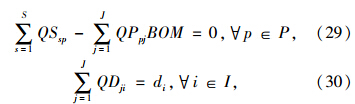
第三部分为库存成本InvetC。在已知上述选址变量和运输量后,通过EOQ模型计算最初订货批量,再结合约束条件进行调整,进而得到满足约束的订货批量和总的库存成本InvetC。
第四部分为关税成本DutyC。以得到的运输量和库存成本为输入数据,利用所建立的关税计算模型,得到各层级的关税成本和总的关税成本DutyC。
按照上述求解思路,可有效地消除所有的约束。因此,适应度函数为:
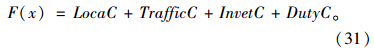
适应度函数确定后,计算各个粒子的适应度值,并对个体极值和群体极值更新,然后对粒子速度和位置更新。针对二进制的离散粒子编码,采用离散空间下的速度和位置更新,公式如下[17]:
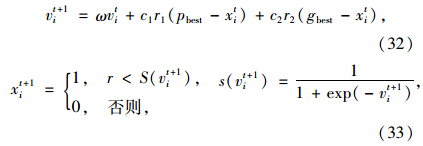
粒子群算法的终止条件为连续20次迭代,适应函数没有明显的改进。 3 算例分析
本文通过一系列算例来验证所建模型的有效性和PSO算法的可行性,分析关税对国际物流网络设计的影响。粒子群算法程序用Matlab 7.10中的M语言编写,测试用的计算机处理器为Intel(R) Core(TM) i5-2410 CPU,单核频率为2.30 GHz,2.0 GB的内存,操作系统为Windows 7家庭普通版。计算时间单位为s。 3.1 算例数据
算例总共有25个:10个算例针对不同的供应链节点数,例如算例“5-10-15-20”表示该算例有5个供应商、10个工厂、15个配送中心和20个工厂;另外15个算例针对在相同供应链节点数下需求大小、单位运输成本和单位库存成本增加不同的比例。
各算例的数据均采用随机方式产生,具体规则如下:供应商的固定选择成本FS和设施(工厂和配送中心)的打开成本FP和FD服从参数为[5 000,15 000]的均匀分布;供应商到工厂的单位运输成本TS服从参数为[5,15]的均匀分布,工厂到配送中心的单位运输成本TP服从参数为[20,50]的均匀分布,配送中心到顾客的单位运输成本TD服从参数为[100,200]的均匀分布,供应商的原材料采购成本PS服从参数为[200,300]的均匀分布,工厂单位生产成本MP服从参数为[1 000,1 500]的均匀分布;工厂成品一次订货成本OP服从参数为[1 500,2 000]的均匀分布,工厂原材料一次订货成本OM服从参数为[2 000,2 500]的均匀分布,工厂成品单位库存持有成本HP服从参数为[150,200]的均匀分布,工厂单位原材料库存持有成本MH服从参数为[50,100]的均匀分布,配送中心订货成本OD服从参数为[3 000,4 000]的均匀分布,配送中心单位库存持有成本HD服从参数为[500,800]的均匀分布;顾客需求d服从参数为[1 000,3 000]的均匀分布。从供应商到工厂和从工厂到配送中心的进口关税税率为相应单位运输成本的0.01倍,从配送中心到顾客的进口关税税率为相应单位运输成本的0.001倍;BOM取值为2。 3.2 算例仿真结果
不同规模测试算例的运算结果如表 1所示。第一列“测试算例”表明了每一个算例中候选供应商、工厂、配送中心和顾客的数量;第二列是每一个算例总的节点数;第三、四和五列是“两阶段网络设计”结果,即先通过网络设计模型得到供应链的网络结构、工厂产量、运输量和库存量等参数后,再计算相应的关税以及总成本(关税成本+网络设计成本);第六、七和八列是“一体化网络设计”结果,即利用本文所建立的考虑关税影响的一体化网络设计模型得到网络设计参数和总成本(关税成本+网络设计成本);第九和十列是两种方法的比较,“节约数”等于第五列的“总成本”减去第八列的“总成本”,节约比例等于“节约数”除以第五列的“总成本”。
| 测试算例 | 总节点数 | 两阶段网络设计 | 一体化网络设计 | 总成本节约 | |||||
| 运算时间 | 关税成本 | 总成本 | 运算时间 | 关税成本 | 总成本 | 节约数 | 节约比例 | ||
| 5-10-15-20 | 50 | 35 | 29 245 642 | 96 395 079 | 102 | 24 981 244 | 92 377 268 | 4 017 811 | 4.17 |
| 5-10-15-30 | 60 | 37 | 45 092 971 | 149 857 565 | 120 | 39 010 476 | 143 975 923 | 5 881 642 | 3.92 |
| 5-10-15-40 | 70 | 39 | 59 538 268 | 197 624 640 | 137 | 52 434 129 | 190 772 316 | 6 852 325 | 3.47 |
| 5-10-15-50 | 80 | 53 | 70 796 148 | 237 092 306 | 113 | 62 837 795 | 229 573 374 | 7 518 933 | 3.17 |
| 5-10-20-50 | 85 | 75 | 68 793 069 | 235 001 587 | 168 | 61 707 800 | 228 694 620 | 6 306 967 | 2.68 |
| 5-10-25-50 | 90 | 68 | 68 202 042 | 234 305 741 | 181 | 58 732 580 | 225 515 692 | 8 790 048 | 3.75 |
| 5-10-30-50 | 95 | 62 | 63 447 350 | 229 475 754 | 217 | 56 602 717 | 223 285 440 | 6 190 315 | 2.70 |
| 5-10-40-50 | 105 | 88 | 62 793 739 | 228 666 413 | 186 | 60 893 084 | 227 322 539 | 1 343 875 | 0.59 |
| 5-20-40-50 | 115 | 94 | 61 748 502 | 227 212 618 | 274 | 56 777 906 | 223 256 416 | 3 956 202 | 1.74 |
| 5-30-40-50 | 125 | 116 | 58 862 369 | 223 429 892 | 399 | 55 470 989 | 220 780 202 | 2 649 689 | 1.19 |
从表 1可以看出,“一体化的网络设计”可以明显降低关税成本和总成本。节约比例最大的算例是“5-10-15-20”,关税成本和总成本的减少都超过4 000 000,节约比例达到4.17%;节约比例最小的算例是“5-10-40-20”,总成本节约数达到1 343 875,节约比例为0.59%。从运算时间来看,本文所建立模型的运算时间明显要长,这是由于考虑关税影响后,模型的复杂度有所增加,但从时间的绝对长度来看是可以接受的。另外,无论采用哪种方法,关税成本占总成本的比例都超过25%,说明关税在供应链网络设计中是一个非常值得重视的因素。
针对算例“5-10-15-20”,需求、单位运输成本和单位库存成本从10%到50%增长情况下的测试结果如表 2所示。可以看出,随着需求、单位运输成本和库存成本的增加,总成本的节约会增大。例如,当需求增加幅度从10%增加到50%时,总成本的节约比例从4.18%增加到4.25%。而且,单位运输成本的增加所带来的总成本节约比例大于需求增加所带来的总成本节约比例。虽然随着单位库存成本的增加,总长成本节约比例有所波动,但总体趋势是增大的。当企业面对需求增大、单位运输成本和库存成本增加时,考虑关税成本的国际网络设计给企业带来的成本节约会更加明显。
| 变化参数 | 增加幅度/% | 不考虑关税影响的网络设计 | 考虑关税影响的网络设计 | 总成本节约 | |||
| 关税成本 | 总成本 | 关税成本 | 总成本 | 节约数 | 节约比例/% | ||
| 需求居中 | 10 | 32 158 226 | 105 958 335 | 27 468 443 | 101 527 712 | 4 430 624 | 4.18 |
| 20 | 35 070 302 | 115 518 634 | 29 955 883 | 110 666 929 | 4 851 705 | 4.20 | |
| 30 | 37 981 931 | 125 076 339 | 32 442 945 | 119 803 252 | 5 273 086 | 4.22 | |
| 40 | 40 893 165 | 134 631 744 | 34 930 714 | 128 929 453 | 5 702 291 | 4.24 | |
| 50 | 43 804 046 | 144 185 092 | 37 412 691 | 138 062 768 | 6 122 324 | 4.25 | |
| 单位运输成本 | 10 | 29 415 032 | 97 228 807 | 24 813 288 | 92 928 675 | 4 300 132 | 4.42 |
| 20 | 29 584 423 | 98 062 534 | 24 942 206 | 93 706 455 | 4 356 079 | 4.44 | |
| 30 | 29 753 813 | 98 896 261 | 25 071 323 | 94 486 021 | 4 410 240 | 4.46 | |
| 40 | 29 923 203 | 99 729 989 | 25 199 672 | 95 278 018 | 4 451 971 | 4.46 | |
| 50 | 30 092 593 | 100 563 716 | 25 328 337 | 96 070 768 | 4 492 948 | 4.47 | |
| 单位库存成本 | 10 | 29 257 065 | 96 461 506 | 24 987 868 | 92 454 613 | 4 006 893 | 4.15 |
| 20 | 29 267 979 | 96 524 976 | 25 056 030 | 92 698 546 | 3 826 430 | 3.96 | |
| 30 | 29 278 447 | 96 585 853 | 25 007 748 | 92 603 834 | 3 982 019 | 4.12 | |
| 40 | 29 288 519 | 96 644 429 | 25 014 607 | 92 658 722 | 3 985 707 | 4.12 | |
| 50 | 31 583 308 | 98 984 389 | 25 022 868 | 92 721 787 | 6 262 602 | 6.33 | |
国际物流网络设计是全球供应链管理的战略决策问题,对跨国企业的利润和竞争力有重要影响。本文针对目前国际物流网络设计中缺乏综合考虑库存成本和关税影响的不足,以供应商、工厂、配送中心和顾客构成的供应链为对象,基于梯级库存持有成本概念,建立了连续需求下考虑关税成本的多层级选址-库存模型。针对模型NP困难特点,设计了PSO智能优化算法。多个算例的仿真运算表明:在国际物流网络设计中,整合关税成本的一体化选址-库存模型是非常有必要的,能够带来明显的成本节约,对于降低企业跨国经营的成本和提高国际竞争力有重要的意义;所建立的模型是有效的,可以用于多层级的国际物流网络设计;设计的PSO算法是可行的,能够在可接受的时间范围内求解较大规模的问题。
| [1] | ARNTZEN B C, BROWN G G, HARRISON T P, et al. Global Supply Chain Management at Digital Equipment Corporation[J]. |
| [2] | HAMAD R, GUALDA N D F. Model for Facilities or Vendors Location in A Global Scale Considering Several Echelons in the Chain[J]. Network Spatial Economies, 2008,8(2/3):297-307. |
| [3] | TSIAKIS P, PAPAGEORGIOU L G. Optimal Production Allocation and Distribution Supply Chain Networks[J]. |
| [4] | BASSETT M, GARDNER L. Optimizing the Design of Global Supply Chains at Dow AgroSciences[J]. |
| [5] | HUCHZERMEIER A, COHEN M A. Valuing Operational Flexibility under Exchange Rate Risk[J]. |
| [6] | DAS K, SENGUPTA S. A Hierarchical Process Industry Production-distribution Planning Model[J]. |
| [7] | BAUMOL W J, WOLFE P. A Warehouse-Location Problem[J]. |
| [8] | MCCANN P. The Logistics Cost Location-production Problem[J]. |
| [9] | NOZICK L K, TURNQUIST M A. Integrating Inventory Impacts into A Fixed-Charge Model For Locating Distribution Centers[J]. |
| [10] | SHEN Z J M. Efficient Algorithms for Various Supply Chain Problems[D]. Evanston, IL: Northwestern University, 2000. |
| [11] | SNYDER L V, DASKIN M S, TEO C P. The Stochastic Location Model with Risk Pooling[J]. |
| [12] | 唐凯, 杨超, 杨君. 带市场选择的联合库存选址模型[J].工业工程与管理,2007,12(5): 5-10.TANG Kai,YANG Chao, YANG Jun. Joint Inventory-Location Models with Market Selection [J]. Industrial Engineering and Management, 2007,12(5):5-10. |
| [13] | 税文兵, 何民, 何明卫. 基于协调补货策略的多产品选址库存联合决策模型[J]. 公路交通科技, 2012, 29(5): 134-139.SHUI Wen-bing, HE Min, HE Ming-wei. A Multi-product Location-inventory Model Based on Coordinated Replenishment Policy[J]. Journal of Highway and Transportation Research and Development, 2012, 29(5): 134-139. |
| [14] | FENG CM, WU P J. A Tax Savings Model for the Emerging Global Manufacturing Network[J]. |
| [15] | 杨维,李歧强.粒子群优化算法综述[J].中国工程科学, 2004, 6(5):87-94.YANG Wei, LI Qi-qiang. Survey on Particle Swarm Optimization Algorithm[J]. Engineering Science, 2004, 6(5):87-94. |
| [16] | AHUJA R, MAGNANTI T, ORLIN J. Network Flows: Theory, Algorithms, and Applications[M]. New York: Prentice Hall, 1993. |
| [17] | KENNEDY J,EBERHART R C. A Discrete Binary Version of the Particle Swarm Algorithms [C]//Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. Orlando: IEEE, 1997:4104-4108. |
 2014, Vol. 31
2014, Vol. 31
