扩展功能
文章信息
- 林志恒, 何兆成, 戴秀斌, 褚俊飞, 沙志仁
- LIN Zhi-heng, HE Zhao-cheng, DAI Xiu-bin, CHU Jun-fei, SHA Zhi-ren
- 考虑降雨影响的城市交通流车速多层线性模型研究
- Research on Urban Traffic Speed Hierarchical Linear Model Considering Rainfall Effect
- 公路交通科技, 2014, 31(10): 119-125
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 119-125
- 10.3969/j.issn.1002-0268.2014.10.019
-
文章历史
- 收稿日期:2013-10-10
2. 东莞中山大学研究院 智能交通工程中心, 广东 东莞 523000
2. Intelligent Transport Engineering Laboratory, Dongguan Institute of Sun Yat-sen University, Dongguan Guangdong 523000, China
平均行驶车速(以下简称车速)是城市道路交通流的主要参数之一,在交通流预测、评价、诱导控制等领域有着广泛的研究和应用。广州地处热带季风气候区,城市交通流受降雨天气的较大影响,因此结合降雨因素的交通流车速短时预测(不大于15 min)是一个重要的研究问题。
降雨天气对城市道路交通流所产生的影响主要表现在以下方面:(1)改变了驾驶员的行驶行为和特性,降雨、降雪和大雾天气降低驾驶员的能见度[1],并缩窄驾驶员的视野[2],使驾驶员的行为变得谨慎[3],从而改变了车辆的跟驰行为。驾驶员为了保持期望的车头间距,车速减慢使得车头时距增加[4]。(2)对交通流运行的通行能力和出行效率造成了负面的影响,降雨对交通强度的影响是显著而且负面的[5]。经研究发现,小雨导致通行能力降低4%~10%,速度降低5%~6.5%;大雨导致通行能力降低25%~35%,速度降低5%~6.5%[6]。(3)恶化了交通运行的安全性,潮湿使得路面的摩擦力下降,车辆容易滑移,直接增加了交通事故的危险[7]。有研究认为降雨天气引发的交通事故是一般天气的2~3倍,尤其是降雨发生在一段干燥天气后危险性更大[8];融合降雨信息可以改善时间序列方法对车速的短期动态预测[9];基于传统交通流理论可以发现降雨量与车速之间的指数模型,并可实现车速的长时预测[10]。但是,上述研究没有考虑到路段因素的影响,因此模型适用性较为有限。
本文的研究目的是将路段间的差异性信息,融进包括降雨量(或称降雨强度)在内的车速短时动态预测模型当中,使得模型具有普遍的适用性,以便于大规模应用。传统理论在考察交通流时,要么没有考虑气象因素或路段因素,要么将交通流因素与气象因素、路段因素并列一起进行分析。以上传统统计方法由于没有考虑数据的层次结构,有可能做出不合理的解释[11],这意味着传统的回归分析方法在分析具有层次结构的交通流数据时存在很大的局限性,即传统线性回归分析的普通最小二乘法估计并不适用于交通流问题的研究[12]。因此,需要采用新型统计技术——多层线性模型(Hierarchical Linear Models,HLM)[13]来研究交通流这种多层数据。多层线性模型或称分层线性模型,是针对具有嵌套、分层结构的数据而提出的一种新型统计技术,与传统统计回归方法相比具有模型假设与实际更为吻合、结果解释更为合理等特点[11]。HLM参数估计的方法是收缩估计(Shrinkage Estimates),优点是可以得到更为精确而有效的估计[14],近年来这一方法已逐渐应用于教育学、心理学、人口学、医学等等领域[15,16]。国外已经成功利用HLM来研究交通的驾驶行为[17]、安全、信号控制等问题,但是就我们所知,国内尚未引入过HLM来研究与交通流相关的问题。
交通流的信息具有嵌套、分层的数据结构:交通流嵌套于路段,而路段嵌套于路网,或者简单地将交通流看成是嵌套于路网。在此,代表数据结构第一层的是交通流,本文将该层称为交通流层,而代表数据结构第2层的是路段或路网,本文将该层分别称为路段层、路网层。例如,在探讨交通流车速的影响因素时,需要考虑的解释变量主要包括流量、密度、占有率等内部因素以及各种气象因素,和交通流所在路段的几何特征、长度、车道数、交叉口密度等路段因素。这些变量分别来自于两个不同的水平,即交通流水平或交通流层(包括交通流内部因素和气象因素)、路段水平或称路段层(路段因素)。这种存在嵌套结构的数据再用以前传统的回归方法,如多元回归分析,将可能得出误差较大甚至错误的分析结果。因为,传统的线性回归模型的基本假设是变量间存在直线关系,变量总体服从正态分布,方差齐性,个体间随机误差相互独立,后2个假设在分层嵌套试验设计中往往难以成立。例如,同一路段的交通流车速可以假设方差齐性,但是不同路段的交通流车速将很难保证方差齐性;不同路段的交通流车速可以假设相互独立,但同一路段的交通流车速由于受相同路段因素的影响,很难保证观察的独立性,而观察独立性正是经典统计技术的基础,显然不符合多层结构的数据。因此如果采用传统的回归分析方法,误差将会扩大。而HLM能够将不同层次的变量分层计算,将误差按层次分解为第一水平的变异和第二水平的变异,并假设第一水平交通流车速间的测量误差相互独立,第二水平由路段带来的误差在不同路段之间相互独立,这样有利于提高变异分解的精度。鉴于多层结构数据在交通流中的普遍性和HLM的优越性,可以将HLM运用于降雨对交通流车速影响的研究中。
本文引入多层线性模型,通过对广州市大约1.7万辆出租车的大规模交通流车速数据和降雨量数据的耦合研究,分析交通流车速的影响因素,并建立一个包括车速、降雨量、路段几何特征、交叉口绿信比等因素在内的短时动态预测新模型:车速-降雨量模型,并对该模型的有效性进行了验证分析,验证的结果说明新模型具有广泛的路段适用性,因而具有大规模应用的潜力。 1 数据采集
研究资料主要包括大规模的交通流平均行驶车速数据(根据准则剔除粗大误差之后的有效样本总量为1 668 634)、降雨量数据(有效样本量为93 462)、路段资料(25个路段)等3部分。25个研究路段离广州市中山大学自动气象检测站的距离都限制在3 km的范围之内,从而保证气象检测站测量出来的降雨量数据与交通流数据比较有效地融合。交通流平均行驶车速数据来源于广州市大约1.7万辆出租车的大规模GPS信号,每个路段每5 min估计一次平均行驶车速,车速估计的方法及精度见文献[18,19];降雨量数据来源于广州市中山大学自动气象检测站,每5 min检测一次降雨量,降雨量的检测单位是0.2 mm[20]。抽取了从2011年6月1日至2012年4月25日一共330 d的车速、降雨量数据,每天从06:00采集到23:55,间隔为5 min,每天216个样本。融合后每个样本记录了每个路段每个采集间隔的时间、平均行驶车速、降雨量、路段长度、车道数、等效交叉口数等信息。 2 考虑降雨影响的交通流车速预测模型的研究 2.1 车速动态影响的分析
已有研究发现,降雨对交通流参数例如车速的影响是显著且负面的[21,22]。很显然需要继续解答的问题就是:降雨显著影响下,车速将会如何变化?它包括如下两点:(1)车速变化量应该如何划分?(2)每一个部分又是如何变化的?
本文提出如下的基本假想来试图解答上述问题:降雨将会引起交通流的变化,车速变化量将由如下3部分来构成:(1)当前交通流的变化而引起的车速变化;(2)降雨的负作用;(3)目前忽略的误差项。
先来讨论车速变化量的第一部分,现有研究发现交通流具有周期性[23],并形成了一系列的研究成果[24],进而成功应用于交通控制[25]。这说明交通流车速将是周期相似变化的,因此在可允许的误差范围内,第一部分可以由每条道路对应历史时刻车速变化量的平均值来分别代表,该值将随着路段、时间的变化而变化。
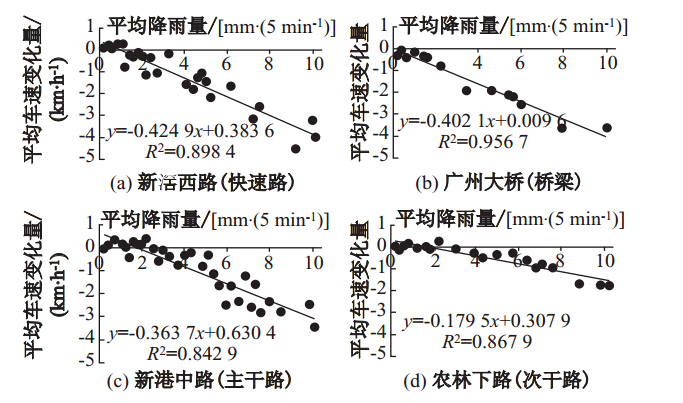
再来讨论车速变化量的第二部分,经观察发现,相同的降雨强度对不同物理特征的路段的交通流车速的影响是不同的。为了说明这一现象,分层抽样研究路网,绘制出如图 1所示的多个散点图,其中横坐标x表示观测时间内某个分组的平均降雨量,记为Rij,表示路段j第i降雨量分组的平均降雨量,其中i=1,2,…,Nj(Nj是路段j降雨量分组的总数),j=1,2,…,J(J为用于建模 的路段总数20);纵坐标y表示车速变化量的实测值与其对应历史平均值之差的平均值,记为ΔVij,表示路段j第i组降雨量对应的平均车速变化量。观察图 1易得:(1)从平均角度来看,可以用线性关系来近似表达降雨量与车速变化量的关系;(2)每条直线的斜率都是不同的,即降雨对车速的影响具有空间变异性;(3)每条直线的截距也是不同的。这说明交通流数据是多层的,因此运用多层线性模型来研究交通流车速问题是合理的。
|
| 图 1 不同类型道路的平均车速变化量与平均降雨强度的散点图 Fig. 1 Scattergram of average speed variation vs. average rainfall intensity of different types of road |
车速变化量的第3部分目前设为误差项。
2.2 考虑降雨影响的车速动态建模
首先建立适用于多层线性模型的多层数据。
层1(或称交通流层,将气象因素视为交通流运行的一部分):因变量是车速变化量ΔVij,第1层的解释变量是降雨量Rij,总共521个有效样本;
层2(或称路段层):第2层的解释变量是“路段长度×车道数”LjLnj、“等效交叉口数”Ij,建模用的路段一共20个(剩余的路段用作验证分析)。
为了统一量度信号控制交叉口对交通流的延误作用,本文引入等效交叉口数Ij的物理概念,记所有路段所有交叉口所有时刻的绿信比均值为λ0(经计算0=0.408),那么路段j的等效交叉口数为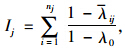 , 式中,Ij为路段j的等效交叉口数,nj为路段j的信号控制交叉口总数,ij为路段j第i个信号控制交叉口的平均绿信比。显然等效交叉口数Ij越大,那么路段j交叉口对整个路段的交通流的延误作用将会越大。
, 式中,Ij为路段j的等效交叉口数,nj为路段j的信号控制交叉口总数,ij为路段j第i个信号控制交叉口的平均绿信比。显然等效交叉口数Ij越大,那么路段j交叉口对整个路段的交通流的延误作用将会越大。
为了正确研究降雨对车速的影响,并考虑路段物理特征对降雨效应的调节作用,进而准确地预测降雨条件下的车速,按照多层线性模型的结构特征,现提出如下的数学假设模型。
模型1:(空模型)考虑不含任意解释变量的2水平模型,这一模型通常用作变量层次分析的基准模型,主要用来检验车速是否存在路段水平上的变异。
层1(或称交通流层、个体水平):
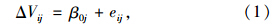
层2(或称路段层、路段水平):
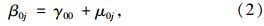
模型2:将交通流层的降雨量Rij纳入空模型以解释降雨引起的车速变化。
层1:
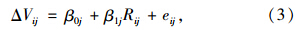
层2:
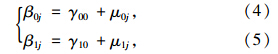
模型3:将路段层的解释变量“路段长度×车道数”(LjLnj)、“等效交叉口数”Ij纳入模型2,以表达降雨对车速影响的空间变异性,同时考虑第2水平解释变量对降雨和车速之间关系的调节作用。
层1:
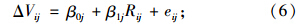

运用SAS的PROC MIXED程序对上述3个模型分别进行了建模。 3 试验结果分析
(1)空模型的估计结果表明,跨级相关系数ICC[26]=0.035 1/(0.035 1+0.561 8)=0.06,这说明约6%的车速变化量是路段之间的差异造成的,根据经验判断的准则,当ICC不小于0.06时,就需要在建模中考虑如何处理组间效应[27]。同时代表路段异质性的估计值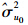 呈统计显著性(
呈统计显著性(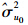 =0.035 1,P=0.026 9),所以利用多层线性模型来分析交通流问题是有必要的。
=0.035 1,P=0.026 9),所以利用多层线性模型来分析交通流问题是有必要的。
(2)模型2的估计结果见表 1。观察表 1的固定效应部分,得:降雨对车速的作用是显著且负面的(γ10=-0.192 6,P<0.000 1)。观察表 1的随机效应部分,得:降雨对车速的影响的确具有普遍的空间变异性(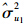 =0.001 503,P=0.002 3)。用RB方法[17]可以估计降雨量对车速变异的可解释比例,加入降雨量之后第1水平残差eij的方差由原来的0.561 8 减小到0.225 3,这说明除了交通流周期性影响之外,降雨强度平均解释了约为59.9%(1-0.225 3/0.561 8)的车速变异。
=0.001 503,P=0.002 3)。用RB方法[17]可以估计降雨量对车速变异的可解释比例,加入降雨量之后第1水平残差eij的方差由原来的0.561 8 减小到0.225 3,这说明除了交通流周期性影响之外,降雨强度平均解释了约为59.9%(1-0.225 3/0.561 8)的车速变异。
| 因变量 | 固定效应 | 随机效应 | |||||
| 参数 | 估计值 | 标准误 | P值 | 参数 | 方差 | P值 | |
| 车速变化量 | γ00 | 0.209 4 | 0.037 3 | <0.000 1 | Var(μ0j):00 | 0.000 01 | 0.000 0 |
| γ10 | -0.192 6 | 0.016 6 | <0.000 1 | Var(μ1j):11 | 0.001 503 | 0.002 3 | |
| 注:γ00为条件总体均数估计; γ10为降雨量的主效应。 | |||||||
(3)模型3的估计结果见表 2。值得注意的是,交通流层的降雨量对车速的负作用依赖于路段层的场景变量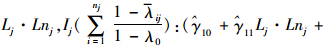
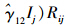 , 这说明交通流层与路段层之间的解释变量存在跨层交互效应,即
, 这说明交通流层与路段层之间的解释变量存在跨层交互效应,即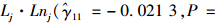
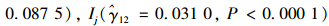 对降雨与车速之间的关系β1j具有边际显著或显著的调节作用,即路段长度越长或车道数越多,降雨对车速的负面效应越大;但是路段的等效交叉口数越大,降雨对车速的负面效应却越小。所以,降雨对车速影响存在空间变异性的根本原因就是:每个路段的几何特征和等效交叉口数都是不同的。同理,路段层的解释变量Lj·Lnj,Ij对车速的效应也分别依赖于交通流层的气象因素
对降雨与车速之间的关系β1j具有边际显著或显著的调节作用,即路段长度越长或车道数越多,降雨对车速的负面效应越大;但是路段的等效交叉口数越大,降雨对车速的负面效应却越小。所以,降雨对车速影响存在空间变异性的根本原因就是:每个路段的几何特征和等效交叉口数都是不同的。同理,路段层的解释变量Lj·Lnj,Ij对车速的效应也分别依赖于交通流层的气象因素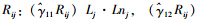 。这与传统认识是截然不同的:气象因素与交通流参数之间的关系是固定的。注:
。这与传统认识是截然不同的:气象因素与交通流参数之间的关系是固定的。注: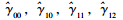 分别为γ00,γ10,γ11,γ12的估计值。eij方差的估计值(
分别为γ00,γ10,γ11,γ12的估计值。eij方差的估计值(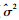 =0.228 3,P=0.000 0)统计上非常显著,表明还需要进一步解释个体变异eij(如交通流的动态变化或其他气象因素等)。
=0.228 3,P=0.000 0)统计上非常显著,表明还需要进一步解释个体变异eij(如交通流的动态变化或其他气象因素等)。
| 因变量 | 固定效应 | 随机成分 | |||||
| 参数 | 估计值 | 标准误 | P值 | 参数 | 估计值 | P值 | |
| 车速变化量 | γ00 | 0.205 8 | 0.040 4 | <0.000 1 | Var(eij):2 | 0.228 3 | 0.000 0 |
| γ10 | -0.216 3 | 0.038 2 | <.000 1 | Var(μ0j):00 | 0.004 9 | 0.313 4 | |
| γ11 | -0.021 3 | 0.012 4 | 0.087 5 | Var(μ1j):11 | 0.002 2 | 0.036 8 | |
| γ12 | 0.031 0 | 0.006 2 | <.000 1 | Cov(μ0j,μ1j):01 | -0.003 1 | 0.270 0 | |
(4)将模型3中的随机成分μ0j+μ1jRij+eij记为εj(t),表示路段j第t时段车速的随机变异。由于降雨对车速造成的影响是负面的,于是可将模型3中位于x轴上方的部分全部设为0。因此,若已知路段j第t-1时段车速的实测值为Vj(t-1),那么下一时段车速的预测值Vj(t)将可估计为:
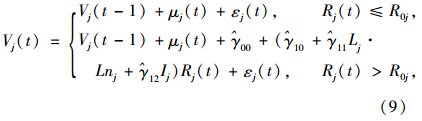
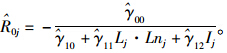 。
。式(9)即为本文构建的车速-降雨量模型。
(5)类似于R2指标,经计算车速-降雨量模型的可解释比例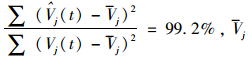 为路段j的平均车速,这说明新模型是有效的。为实证新模型的有效性,并与传统线性模型进行比较分析,挑选了代表性意义较强的某持续性降雨时段分别进行了动态预测。该持续性降雨时段为2012-05-27 14:00—17:40,具有如下特点: (1)囊括了交通流的平峰、高峰的2种状态;(2)囊括了各个降雨等级的样本;(3)存在降雨强度平稳变化的时段,也存在降雨强度突变的时段。
为路段j的平均车速,这说明新模型是有效的。为实证新模型的有效性,并与传统线性模型进行比较分析,挑选了代表性意义较强的某持续性降雨时段分别进行了动态预测。该持续性降雨时段为2012-05-27 14:00—17:40,具有如下特点: (1)囊括了交通流的平峰、高峰的2种状态;(2)囊括了各个降雨等级的样本;(3)存在降雨强度平稳变化的时段,也存在降雨强度突变的时段。
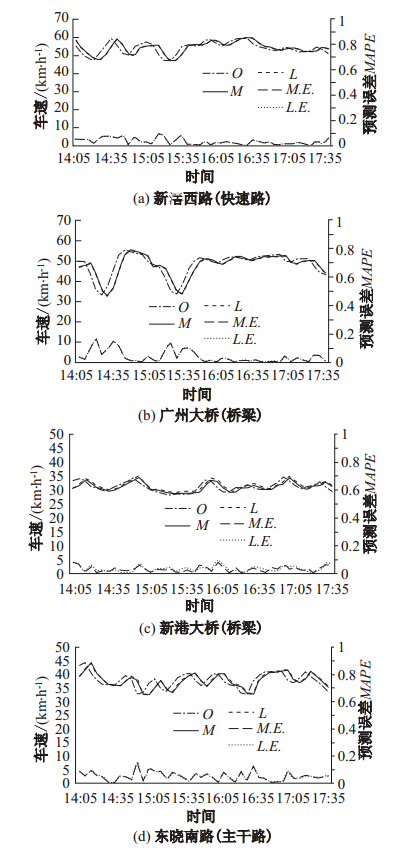
图 2是没参与建模的4个路段分别进行动态预测的曲线图,其中,横坐标为时间,左纵坐标为交通流车速的实测值或预测值,右纵坐标为预测相对误差的绝对值;O为车速的实测值,M为交通流车速-降雨量模型的预测值,L为每个路段分别建立的线性模型的预测值,M.E.为交通流车速-降雨量模型的预测误差,L.E.为每个路段的线性模型的预测误差。动态预测的结果见表 3,其中预测可靠性指的是绝对误差在5%以内的预测所占的比例。注:每个路段分别根据各自的降雨量与车速数据建立的线性模型只适用于本路段,即表 3的线性模型部分。
|
| 图 2 车速-降雨量模型与线性模型短时动态预测车速的对比图 Fig. 2 Comparison of short-term dynamic speeds predicted by speed-rainfall model and linear model |
| 路段名称 | 道路类型 | 车速-降雨量模型 | 线性模型 | ||
| 预测误差 MAPE | 预测可靠性 (<10%) | 预测误差 MAPE | 预测可靠性 (<10%) | ||
| 新滘西路 | 快速路 | 3.63 | 100 | 3.65 | 100 |
| 广州大桥 | 桥梁 | 4.28 | 88.63 | 4.31 | 86.36 |
| 新港西路 | 主干路 | 3.16 | 100 | 3.62 | 100 |
| 东晓南路 | 主干路 | 5.14 | 93.18 | 5.32 | 90.91 |
观察表 3得:(1)车速-降雨量新模型的平均预测误差为4.05%,平均可靠性为95.45%,这说明降雨条件下,新模型对车速的短时预测将非常有效。(2) 新模型与各个路段分别建立的线性模型相比较,多层模型都略微改善预测的精度。(3)不管快速路、桥梁还是主干道,新模型与各个路段各自的线性模型的预测时序图、预测误差图都几乎重叠,这说明相较于传统交通流模型,由于考虑了交通流的空间变异性,新模型具有较好的综合识别各个路段物理特征的能力,车速-降雨量模型具有路段适用性广的突出优点。这进一步说明,多层线性模型将有利于加深我们对交通流理论的认识。 4 结论
由于路段间的物理特征存在显著的差异,因此交通流信息存在嵌套、分层的数据结构,所以相比于传统交通流理论模型,采用多层模型(如HLM)来研究交通流问题将更为合理。而且从多层模型的估计原理可以看出,相对于传统回归方法,多层模型(如HLM)拥有众多优点,将有利于加深我们对道路交通流理论的认识。
多层线性模型的研究结果说明,交通流数据的多层性使得降雨对车速的影响具有普遍的空间变异性,因此应用HLM来构建的交通流车速-降雨量性模型具有路段适用性广的突出优点。
交通流层与路段层的变量存在跨层交互效应,例如降雨对车速的效应将随着路段几何特征、等效交叉口数的不同而不同。路段越长、车道数越多,降雨对车速的负面影响越大;但是,信号控制交叉口绿信比越小,降雨对车速的负作用将会越小。反之,路段几何特征、等效交叉口数对交通流的影响也依赖于气象因素(如降雨强度),这与交通流参数跟气象因素、路段因素具有同层关系的传统认识明显不同。
车速-降雨量新模型包括了车速、降雨量、路段几何特征、信号控制交叉口绿信比等诸多参数,较为成功地揭示了交通流影响因素之间的相互关系,并且具有大规模应用的潜力。但是多层线性模型的统计结果也表明:还需要考虑交通流的动态影响或其他气象因素的作用,因而该模型还需要改进。
| [1] | MORRIS R S, MOUNCE J M,BUTTON J W,et al. Visual Performance of Drivers during Rainfall [J]. Transportation Research Record, 1977, 628: 19-25. |
| [2] | VAN DER H M,ROTHENGATTER T,MEIJMAN T. The Effect of Reduced Visibility and Time Pressure on Drivers' Distance-keeping Behaviour [J]. Vision in Vehicle-VII, 1999,7: 311-318. |
| [3] | EISENBERG D. The Mixed Effects of Precipitation on Traffic Crashes [J]. |
| [4] | RAHMAN A, LOWNES N E. Spatially Compatible Rainfall-Speed Analysis [C] //Proceedings of the 89th Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board,2010. |
| [5] | COOLS M, MOONS E, WETS G. Assessing the Impact of Weather on Traffic Intensity [J]. |
| [6] | SMITH B L,BYRNE K G,COPPERMAN R B,et al. An Investigation into the Impact of Rainfall on Freeway Traffic Flow [C] //Proceedings of the 83rd Annual Meeting of the Transportation Research Board. Washington, D. C. : Transportation Research Board, 2004. |
| [7] | ANDREY J, MILLS B, VANDERMOLEN J. Weather Information and Road Safety[R]. Toronto: Institute for Catastrophic Loss Reduction, 2001. |
| [8] | BRODSKY H. Risk of a Road Accident in Rainy Weather [J]. |
| [9] | TSIRIGOTIS L,VLAHOGIANNI E I,KARLAFTIS M G. Does Information on Weather Affect the Performance of Short-term Traffic Forecasting Models[J]. |
| [10] | LAM W, TAM M, CAO X, et al. Modeling the Effects of Rainfall Intensity on Traffic Speed, Flow, and Density Relationships for Urban Roads [J]. |
| [11] | 雷雳, 张雷. 多层线性模型的原理及应用 [J]. 首都师范大学学报:社会科学版,2002,145(2):110-114. LEI Li, ZHANG Lei. Principle and Application of the Hierarchical Linear Models[J]. Journal of Capital Normal University: Social Sciences Edition, 2002,145(2):110-114. |
| [12] | BRYK A S,RAUDENBUSH S W. Hierarchical Linear Models: Applications and Data Analysis Methods [M]. London: Sage Publication,1992. |
| [13] | 张雷, 雷雳. 多层线性模型应用 [M]. 北京:教育科学出版社, 2005. ZHANG Lei, LEI Li. Application of Multilevel Linear Models[M]. Beijing: Education Science Press, 2005. |
| [14] | 蒋莉, 杨志明, 姚树桥. 学生高考语文成绩影响因素的多层线性分析[J]. 中国临床心理学杂志,2005,13 (4): 414-417. JIANG Li, YANG Zhi-ming, YAO Shu-qiao. Analysis of Influencing Factors on the Chinese Achivement Test in the College Entrance Examination: A Hierarchical Linear Model[J]. Chinese Journal of Clinical Psychology, 2005,13 (4): 414-417. |
| [15] | RAUDENBUSH S W,BRYK A S. Hierarchical Linear Models: Applications and Data Analysis Methods [M]. 2nd ed. Thousand Oaks, CA: Sage Publications,2002. |
| [16] | 蔡永红, 姜勤德. 统计在社会科学领域应用的新进展及反思 [J]. 统计研究,2006(2): 66-69. CAI Yong-hong, JIANG Qin-de. The Latest Development of Application of Statistics to the Field of Social Sciences and the Relevant Reconsiderations[J]. Statistical Research, 2006 (2): 66-69. |
| [17] | ROMAIN B,NOUR-EDDIN E F,FLORIAN D V. Multilevel Assessment of the Impact of Rain on Drivers' Behavior [J]. Journal of the Transportation Research Board,2009,2107(1): 134-142. |
| [18] | LONG CHEU R,XIE C,LEE D H. Probe Vehicle Population and Sample Size for Arterial Speed Estimation [J]. |
| [19] | ZENG W L,HE Z C,LU R Q,et al. Freeway Segment Speed Estimation Model based on Distribution Features of Floating Car Data [C] //Presented at 91rd Annual Meeting of the Transportation Research Board. Washington, D.C.:Transportation Research Board, 2011. |
| [20] | 刘永红, 冯婷, 蔡铭. 广州灰霾现象特征分析 [J]. 环境科学研究, 2011,24(10): 1081-1087. LIU Yong-hong, FENG Ting, CAI Ming. Characteristics of the Haze Phenomenon in Guangzhou[J]. Research of Environmental Sciences, 2011, 24(10): 1081-1087. |
| [21] | 叶佳缘, 杨赛霓, 刘浩. 降雨对高速公路小型车行程时间的影响 [J]. 公路交通科技, 2012, 29(11): 135-139. YE Jia-yuan, YANG Sai-ni, LIU Hao. Impact of Rainfall on Freeway Travel Time for Passenger Cars[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 135-139. |
| [22] | DARCIN A, VIRGINIA P S,ALEXANDER S. Impacts of Weather on Traffic Flow Characteristics of Urban Freeways in Istanbul [J]. Procedia Social and Behavioral Sciences, 2011(16): 89-99. |
| [23] | 欧晓凌, 裘刚, 张毅,等. 城市交通流信息相似性分析与研究 [J]. 中南公路工程, 2003,28(2): 4-7. OU Xiao-ling, QIU Gang, ZHANG Yi, et al. Analysis of Similarity for Urban Traffic Volumes[J]. Central South Highway Engineering, 2003, 28(2): 4-7. |
| [24] | 夏冰, 董菁, 张佐. 周相似特性下的交通流预测模型研究 [J]. 公路交通科技, 2003,20(2): 73-76. XIA Bing, DONG Jing, ZHANG Zuo. Study on the Prediction for Link Traffic Flow Based on Weekly Similarity[J]. Journal of Highway and Transportation Research and Development, 2003, 20(2): 73-76. |
| [25] | JIANG Xian-cai, SU Xiao-hong, MA Pei-jun. Delay Model of Actuated Signal Control Based on the Traffic Flow Running Similarity Principle[C] //Proceedings of the 3rd International Conference on Power Electronics and Intelligent Transportation System. Shenzhen: IITA Association, 2010: 262-265. |
| [26] | HOX J J. Multilevel Analysis, Techniques and Applications [M]. Mahwah, NJ: Lawrence Erlbaum Associates,2002. |
| [27] | 周皓, 巫锡炜. 流动儿童的教育绩效及其影响因素: 多层线性模型分析 [J]. 人口研究, 2008,32(4): 22-32. ZHOU Hao, WU Xi-wei. School Performance of Migrant Children and Its Determinants: A Hierarchical Linear Model Analysis [J]. Population Research, 2008,32(4): 22-32. |
 2014, Vol. 31
2014, Vol. 31
