扩展功能
文章信息
- 张驰, 郭鑫鑫, 崔卜心
- ZHANG Chi, GUO Xin-xin, CUI Bu-xin
- 不均匀积水条件对路面行车安全的影响
- Influence of Uneven Wet Pavement Surface Condition on Driving Safety
- 公路交通科技, 2014, 31(10): 104-111
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 104-111
- 10.3969/j.issn.1002-0268.2014.10.017
-
文章历史
- 收稿日期:2013-12-9
汽车在不均匀积水路面上行驶时,轮胎易产生打滑甚至水漂危险,汽车的操纵稳定性和刹车性能急剧下降,严重影响交通安全[1]。由水漂引起的侧滑等行车安全问题是目前雨天交通事故发生的最主要的原因[2]。因此,路面侧滑等横向稳定性问题是雨天事故研究的重点。
国外T. F. Fwa等人通过建立轮胎-水流-路面的三维有限元模型,应用CFD仿真方式证明了轮胎充气压力、轮胎花纹与车轮荷载对临界水漂速度有明显的影响,并在此基础上建立了不同影响因素条件下的临界水漂速度预测模型[3,4,5,6]。现在国内许多专家对湿滑路面稳定性进行了大量的研究。季天剑等人提出了基于人工神经网络的道路表面水膜厚度预测模型,并通过建立轮胎的三维有限元模型得到了积水路面的部分滑水附着系数、行车速度和路表水膜厚度间的相互关系[7,8,9]。徐进等人应用ADMAS仿真模型对直线段积水路面上的汽车行驶情况进行模拟,指出汽车在积水路段发生偏驶或者侧滑的主要是由轮胎在不同路面情况下(干燥路面和积水路面)的轮周接地线速度的差异所致,并以此对汽车在不同附着系数的路面工况下汽车的横向稳定性进行了研究[10]。李长城等人将积水路段上设计停车视距作为车辆安全性行驶速度的约束条件,以积水路面实际附着系数为变量,得到了车辆在不同设计速度与附着系数下的临界安全车速[11]。董斌等人通过FLUENT流体仿真方法建立了积水路面上轮胎与路面的三维有限元模型,从而得到了车速、水膜厚度与轮胎花纹深度对轮胎所受动水压强的影响[12]。现有的研究主要是对水漂的影响因素以及路面积水附着系数等水漂机理方面的研究,对于路面积水程度对汽车侧滑影响的研究仅是一些定性分析,而不同积水路面下车辆侧滑的定量研究相对较少。
本研究在建立轮胎-地面-水流的三维有限元模型的基础上,应用Fluent微观流体力学仿真软件模拟了轮胎在不同水膜厚度和不同汽车行驶速度条件下所受到动水压力的理论变化值,结合车辆动力学原理,从轮胎与地面的摩擦力和侧转角的角度定量地分析了轮胎在不同水膜厚度和行驶速度下车辆侧滑的严重程度,进而对积水路面车辆横向稳定性进行了研究和探讨。 1 车辆操纵横向稳定性机理分析
当汽车一侧行驶在积水路面上时,汽车左右驱动轮与地面间的摩擦力会出现差异,从而导致汽车发生侧滑甚至事故的产生。
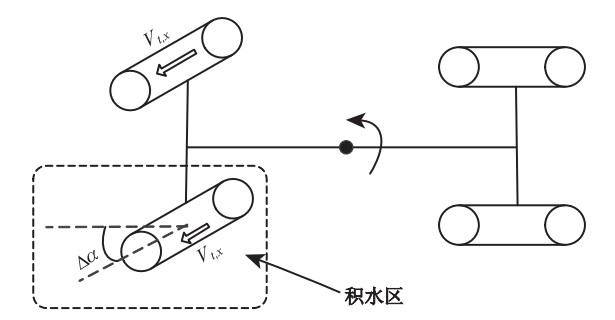
图 1所示为积水路面上的汽车行驶状况,假设汽车的前轮为驱动轮,且汽车左侧前轮以一定速度行驶在积水路面上,右侧前轮行驶在干燥路面上。此时浸水轮胎(左侧轮胎)的静摩擦力会减小,而汽车前轴为主动轴,轮胎摩擦力提供汽车前进的动力,而浸水轮胎摩擦力的减小导致其与路面的附着系数降低,浸水轮胎单位时间内相对于右侧轮胎做减速运动,导致汽车向左侧偏转,当侧转角差Δα大于90°时,汽车就会发生横向侧滑。以右侧轮胎为参照系,在某一段时间t内,浸水轮胎的相对侧滑为其原地打滑的长度,即为两个前轮的相对运动距离差。同时积水区越长,两个轮胎的速度差就越大,车轮侧滑的危险性就越高。事实上,浸水轮胎自身也会发生侧滑现象,而且运动过程十分复杂,此时轮胎的横向侧滑更为严重,危险性会更高。
|
| 图1 积水路面车辆行驶动力学模型 Fig.1 Dynamics model of vehicle on wet pavement |
假设浸水轮胎不产生横向侧滑,且右侧前轮的纵向加速度a为:
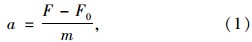
当汽车两侧驱动轮在干燥路面上匀速行驶时,F=F0,即纵向加速度a=0;而当汽车左侧驱动轮驶入积水区域时,由于汽车受到水流的动水压力的作用,F0开始减小,汽车左侧车轮开始产生纵向加速度(a0),这使得汽车左右前轮轮轴处的速度开始不同,定义轮周接地线速度为ωact[10],则:

随着汽车左侧前轮轮心速度的减小(如图 1所示),其轮周接地线速度也会相应减小,从而其在单位时间t内的位移也会减小,假设时间t内两侧轮胎位移分别为L1,L2,则:
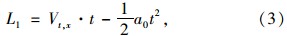

由此可以看出,汽车前轮部分将以浸水轮胎(左侧前轮)为圆心,前车轴为转动半径作圆周变加速运动,且t时刻轮胎的相对横向侧转角差Δα(图 1所示)为:
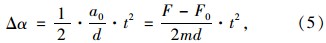
为防止产生惯性移动而失控,一般驾驶员打方向盘最好在一圈以内,即汽车偏转的角度左右各应保持在25°之内[13]。当汽车侧转角的相对差值超过驾驶员的最佳控制角度范围时,汽车的操纵稳定性会下降,导致汽车发生侧滑甚至发生事故。因此本文从积水路面轮胎-路面摩擦力及汽车在积水区的侧转角方面研究分析行车速度及路表水膜厚度对侧滑严重程度的影响,从而为驾驶员在积水路面上行驶时提供一些指导。
2 轮胎-路面-流体模型的建立 2.1 锁轮模型
在一般静止参考系里面,模型模拟的是车轮以一定的速度行驶在有一定厚度水流的路面上。为了模型的简化,可转化为以移动车轮为参考系,即模型可转化为一定厚度的流体(水流和空气)以一定的速度流向固定的车轮(锁轮)[5]。在本文中,外界温度为20 ℃,并且当车轮下的平均动水压力等于轮胎压力,即动水浮力等于车轮荷载时,可认为汽车发生水漂。
进行汽车操纵动力学模型分析选取的车型为目前我国的典型车型,前轮距为d=1 550 mm,单个车轮所受荷载为P=4 218.3 N。代表轮胎选用P225/55R14 95 V典型轮胎,轮胎内压为pi=200 kPa,轮胎半径r=326.95 mm,轮胎宽度为225 mm。
匈牙利学者G.Komandi根据不同尺寸轮胎在不同气压条件下在混凝土路面上进行的大量试验得到了轮胎变形模型的经验公式[14]:
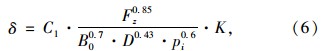
吉林大学汽车地面力学研究室与长春汽车研究所的试验研究指出,轮胎的接地形状大多介于矩形和椭圆形之间。为了简化数值分析,将接地面积简化为矩形,表 1为各种轮胎的s、t值,由此推导出了轮胎与地面的接触面积A的公式[15]:
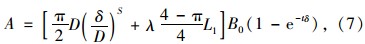

| 轮胎类型 | 5.60R16 | 5.60-16 | 5.00-10 | 4.00-12 |
| 结构类型 | 子午线 | 斜交 | 子午线 | 斜交 |
| 层级数 | 6 | 6 | 4 | 6 |
| s | 0.557 | 0.553 | 0.576 | 0.559 |
| t | 122.7 | 108.9 | 181.1 | 113.8 |
由上可得到轮胎胎面与地面间的接触面积A=391.3 cm2,轮胎的压平量为δ=16 mm。 2.2 路表面模型
本文将光滑平整路面模型作为本次研究的路面模型,即该路面上的平均构造深度为0。因为路表平均构造深度对水漂的影响要远远小于车辆行车速度和水膜厚度对水漂的影响[6],所以为简化模型的建立,采用平均构造深度为0的路表面,并以此应用Fluent有限元软件来建立k-ε湍流模型。
2.3 流体模型
由于在模拟过程中要考虑流体(水流和空气,表 2)的湍流作用,本文采用非定常三维可压缩黏性流动方程作为流体的控制方程。 2.3.1 流体连续性方程(守恒形式):
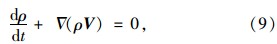
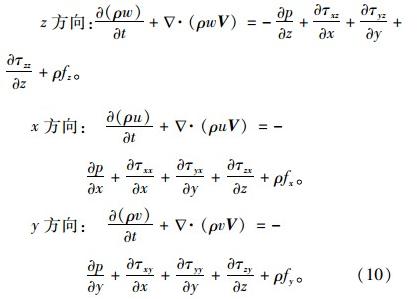

本文选取RNG k-ε模型作为湍流模型,通过在大尺度运动和修正后的黏度项体现小尺寸的影响,而使这些小尺寸运动有系统地从控制方程中去除,可以更好地处理高应变率及流线弯曲程度较大的流动:
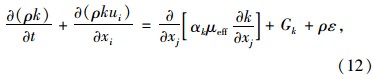
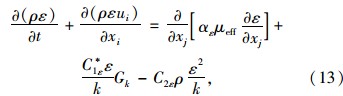
| 流体 | 参数 | ||
| 密度/(kg·m-3) | 动态黏滞度/ [(N·s)·m-2] |
运动黏度/ (m2·s-1) | |
| 水 | 998.2 | 1.002×10-3 | 1.004×10-6 |
| 空气 | 1.204 | 1.82×10-5 | 1.51×10-5 |
| 注:空气参数值是在标准大气压下测得。 | |||
本试验轮胎凹槽内水流的流动的Reynolds数大于8000,因此必定会发生湍流现象。湍流运动内部微观结构比层流复杂很多,其中存在大量作杂乱无章运动的微小漩涡,这些漩涡不断产生、发展、衰减和消失,使得液体质点在运动中不断地相互混掺,质点的流速矢量以及压强、切应力等其他运动物理量都在随时间不断变化,所以用一般的方程是难以对其进行模拟分析的。
基于以上原因,本文选取了VOF(Volume of Fluid)模型。VOF模型通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟两种或三种互不相容的流体(如水流和空气流),对分层的或自由表面流的模拟较为精准。
用各层流体相的连续性方程可以对相间的运动物理量进行模拟。对于第q相流体而言,Fluent运用的流体连续性方程为:
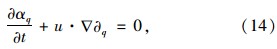
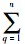 q=1。
q=1。2.3.3 流体边界条件
依据垂直应力及接地尺寸的特性,分析范围x,z边界尺寸为80 cm×100 cm,y方向深度尺寸为5 cm,空气的入口深度根据水膜厚度的不同进行调整。道路是水平和深度方向为无限、宽度方向为有限的三维结构,而Fluent只能计算有限尺寸下流体的力学反应值,但当将分析范围取到足够大时,计算结果应该是接近真实反应值的[15]。
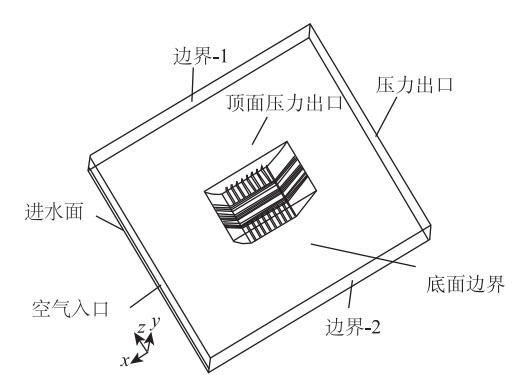
为了模型的简化,即将模型转化为车轮保持固定,流体(空气和水流)以一定的速度(90 km/h)相对于轮胎运动。在Fluent中设置了空气和水的速度入口(inlet-water、inlet-air),壁面wall-1和wall-2的粗糙高度KS为0,粗糙度常量CS为0.5。因为本文主要研究的是轮胎迎水面上的动水压力的变化情况,所以模型中将轮胎的后部、侧部及上部作为压力出口,并且定义wall-ground以一定的速度相对于轮胎运动(模型边界类型见图 2)。本试验模型中选取的车轮胎面花纹深度为7 mm来模拟一般轮胎,根据轮胎与地面的接触面积和模型的简化处理,将接地胎面纵、横向花纹作如图 3所示划分,并取轮胎胎面前端和地面-轮胎接触面处对水流流速和压强进行研究。但值得注意的是不同的边界条件对计算结果的迭代次数和收敛性是有影响的。
|
| 图2 模型边界条件的设置示意图 Fig.2 Schematic diagram of setting model boundary conditions |

|
| 图3模型网格划分示意图 Fig.3 Schematic diagram of model meshing |
由于轮胎与地面之间的部分网格尺寸和倾斜度变化较大,若用六面体网格对其划分较为复杂且计算量大。为将模型进行简化处理,本文采用了Tet/Hybrid网格单元,将四节点的四面体和六节点的楔形单元网格应用于该有限元体积模型,并且在轮胎与地面接触部分对其进行网格细化处理。本文中模型内总共含有769 562个网格单元,如图 3所示。 3 模型仿真及其结果分析
本文应用Fluent模拟汽车以不同的速度(80~120 km/h)在不同的水膜厚度(5~12 mm)上的行驶情况,以此得到雨天不同水膜厚度和汽车行驶速度对轮胎的动水压强大小和分布的影响情况,并根据轮胎所受的动水压强的变化研究轮胎抗滑性和汽车操纵稳定性。 3.1 水膜厚度和速度对轮胎动水压强的影响分析
通过改变水膜厚度和行驶速度两个参数,应用Fluent软件进行仿真,结果如图 4所示。从图中可以看出汽车行驶速度和路表水膜厚度均会引起轮胎所受动水压强的增大。当水膜厚度小于轮胎花纹深度(7 mm)时,如图 4中(a)、(d)和(g)所示,轮胎所受动水压强随汽车行驶速度的增大变化不明显;而当水膜厚度超过轮胎花纹深度时,轮胎所受动水压强会随汽车行驶速度的增大而明显增大(如图 4中(a)、(b)和(c)所示)。这是因为,当水膜厚度小于轮胎花纹深度(7 mm)时,轮胎沟槽内的积水能够及时排除,产生的动水压强增加较慢;但是当水膜厚度大于7 mm时,轮胎沟槽内产生积水,胎面花纹不能将轮胎下的水流及时排除,导致轮胎前端动水压强 增大,当动水浮力等于轮胎所受荷载时,轮胎与路面完全脱离接触,就会出现完全滑水状态。

|
| 图4不同水膜厚度和行驶速度下轮胎所受动水压强 Fig.4 Hydrodynamic pressure intensity that tire suffered in different water film thicknesses and vehicle speeds |
当汽车速度一定时,随着水膜厚度的增加,轮胎所处动水高压区的面积将增加,由图 4中的(d)、(e)和(f)图可以看出,动水高压区会由轮胎中间向轮胎边缘呈近似三角分布。当轮胎行驶在较深的水面上时,轮胎底面的中间部分会持续在动水高压区运动,所以将会首先发生水漂现象,同时因此会导致轮胎极易发生左右摆动而造成驾驶稳定性的下降。
|
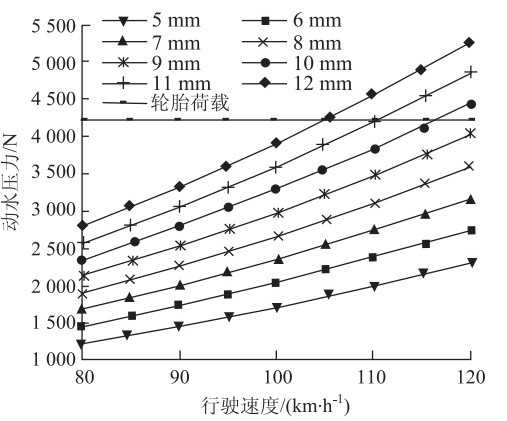
| 图5 轮胎所受动水压力随水膜厚度和速度的变化曲线 Fig.5Curves of hydrodynamic pressure varying with water film depth and speed |
由图 5可知,随着水膜厚度和行驶速度的增加,轮胎前端所受动水压力会逐渐增大。在相同速度条件下,水膜厚度每增加1 mm,轮胎所受动水压强会增加2 kPa,水膜厚度与动水压强表现为近似线性增加的关系,同时高压区域面积将会平均增加约600 mm2;而在一定水膜厚度上行驶时,行驶速度每增加10 km/h,轮胎所受动水压强平均增加81.5 kPa,行驶速度与动水压强同样表现为近似线性增加的关系。对数据进行二元回归分析,得到以下公式:
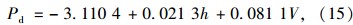

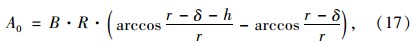
根据国内外文献[4]对临界水漂速度的影响研究,将文献中的实测条件输入至本模型进行分析计算,得到了在不同试验条件下的模拟临界水漂速度。本文将模拟临界水漂速度与真实测量临界水漂速度进行对比分析,如表 3所示:
| 数据来源 | 测试条件 | 实测水漂速度/ (km·h-1) |
模拟水漂速度/ (km·h-1) | |||||
| 轮胎类型 |
路表构造 深度/ mm |
水膜厚度/ mm |
轮胎花纹凹 槽深度/ mm |
轮胎充气 压力/kPa |
轮胎荷载/ N | |||
|
Horne,W. B. & U. T. Joyner. |
6.50-134 花纹轮胎 | 0 | 7.62 | 6.36 | 186.2 | 3 714 | 90.10 | 93.32 |
| Hayes,G. G.,D. L. Ivey & B. M. Gallaway |
ASTM E501 花纹轮胎 | 0 | 9.53 | 1.59 | 165.5 | 4 830 | 82.06 | 84.22 |
|
Balmer,G. G., & B. M. Gallaway |
ASTM E501 花纹轮胎 | 0 | 6.35 | 1.59 | 124.1 | 4 830 | 74.01 | 75.39 |
由表 3可以看出,计算机模拟的临界水漂速度与实地验证的临界水漂速度相差不大,误差率约为2%,由此可证明计算机水漂模型的正确性。由于实验室模拟的研究模型使用的轮胎为ASTM E501标准轮胎,属于美国标准试验轮胎,而考虑到该轮胎无法匹配本文所选车型,因此本文选用了目前汽车较为常用的P195/60 R14 86H型轮胎,然而临界水漂速度的预测结果却相差不大(5%),可以证明本试验的轮胎-流体-路面模型的准确性及适用性。 3.2 雨天汽车操纵稳定性分析
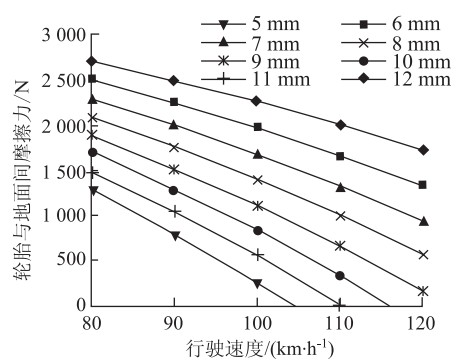
根据动水压力的仿真数据对积水路面上轮胎-路面间的摩擦力的计算结果如图 6所示。从图中可以看出随着路表水膜厚度和行车速度的增加,路面-轮胎间摩擦力非线性减小。当水膜厚度小于7 mm,汽车以低速(<100 km/h)行驶在积水路面上时,摩擦力随单位水膜厚度的变化值近似相等,约为 200 N;当行车速度介于100 km/h和120 km/h之间时,摩擦力减小率约为300 N/mm。当水膜厚度大于7 mm,汽车低速(<90 km/h)行驶在积水路面时,摩擦力减小率约为300 N/mm,车速介于90 km/h 与100 km/h之间时,摩擦力减小率约为400 N/mm;而当车速为100~120 km/h时,摩擦力随单位水膜厚度的变化值达到500 N。
|
| 图6 轮胎与地面间摩擦力随水膜厚度和速度的变化曲线 Fig.6 Curves of friction between tire and pavement varying with water film depth and speed |
一般新轮胎与干燥路面的附着系数为0.90[14],此时轮胎-路面间最大静摩擦力为3 796.47 N,从图 6中可以看出当车辆以120 km/h的速度行驶在水膜厚度为12 mm的路面时,轮胎所受的摩擦力小于500 N,这与干燥路面上轮胎所受的摩擦力相差很大,也就解释了汽车左右轮分别行驶在干燥和积水路面时,路表水膜厚度越大,行驶速度越大,发生侧滑的可能性就越高的原因。
左右轮所受摩擦力的不同导致车辆的横向稳定性下降,在此种情况下,驾驶员一般会控制方向盘对汽车侧偏进行调整,而驾驶员的反应时间一般为0.3 s,因此进入积水区2 s内车辆的相对侧转角差值Δα的大小很大程度上代表了车辆侧滑的危险性。经式(2)计算可得,汽车左右主动轮以不同速度分别在不同水膜厚度的积水路面和干燥路面上行驶时,其相对侧转角差Δα的变化情况如表 4所示。
| 速度/ (km·h-1) | 水膜厚度/mm | |||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 80 | 11.778° | 14.081° | 16.282° | 18.399° | 20.587° | 22.696° | 24.847° | 27.057° |
| 90 | 14.049° | 16.733° | 19.340° | 21.906° | 24.546° | 27.049° | 29.586° | 32.175° |
| 100 | 16.483° | 19.698° | 22.804° | 25.769° | 28.901° | 31.899° | 34.867° | 37.879° |
| 110 | 19.346° | 23.013° | 26.537° | 30.038° | 33.709° | 37.247° | 40.689° | 40.816° |
| 120 | 22.372° | 26.602° | 30.675° | 34.765° | 39.025° | 40.816° | 40.816° | 40.816 |
由表 4可以看出,汽车低速(<90 km/h)行驶在薄层积水路面上(水膜厚度<8 mm)时,1 s后汽车的相对侧转角差变化不大,驾驶员可以通过操纵方向盘来控制行车轨迹。但当车速大于90 km/h,积水区水膜厚度大于9 mm时,汽车的相对侧转角差已超过了最佳控制角度,此时汽车操纵稳定性开始下降,有发生侧滑的可能,驾驶员需要及时调整方向盘。因此,在积水路面行驶时,汽车最好以低速(<90 km/h) 行驶;当路面积水较厚时,车速不应高于80 km/h,并且要及时调整方向盘以保证汽车在可控范围内。
| 速度/(km·h-1) | 水膜厚度/mm | |||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 80 | 47.114° | 56.324° | 65.128° | 73.596° | 82.349° | 90.785° | 99.387° | 108.226° |
| 90 | 56.194° | 66.933° | 77.362° | 87.624° | 98.186° | 108.196° | 118.344° | 128.702 |
| 100 | 65.933° | 78.791° | 91.215° | 103.075° | 115.606° | 127.597° | 139.467° | 151.517 |
| 110 | 77.382° | 92.053° | 106.147° | 120.153° | 134.836° | 148.988° | 162.757° | 163.265 |
| 120 | 89.490° | 106.407° | 122.699° | 139.060° | 156.102° | 163.265° | 163.265° | 163.265 |
由表 5可以看出,当水膜厚度超过8 mm,且行驶速度大于90 km/h时,汽车的相对侧转角差已超过90°,即使水膜厚度小于9 mm,车辆以较高速度行驶时,也会产生这种情况。此时车尾甩动惯性力会使汽车发生过度转向,后轮因侧滑而使得车尾向前甩,从而使汽车滑离原有轨迹,汽车发生横向侧滑。驾驶员应及时将方向盘转至侧滑的一侧方向以减小车尾甩动惯性力,这样可以缓解转向过度,即方向盘的转动应该与车尾侧滑的方向相同。同时应当缓慢减小行车速度,直至汽车得到完全控制或者停下后,才可以继续慢慢加速行驶。由表 4、表 5还可以看出,当行驶速度一定时,相对侧转角差与水膜厚度呈近似线性关系;而当路表水膜厚度一定时,随着汽车行驶速度的增加,并且以增加率逐渐增大的非线性趋势增加。 4 结语
(1)随着路表水膜厚度的增加,动水高压区面积增大,且由轮胎中间向边缘呈近似三角分布。当水膜厚度小于胎面花纹深度7 mm时,汽车行驶速度对动水压强的影响较小;当水膜厚度大于7 mm时,随着行车速度的增加,动水压强呈非线性的趋势增大。
(2)随着路表水膜厚度和行车速度的增加,路面-轮胎间摩擦力非线性减小。当汽车以100~120 km/h 的车速行驶在积水路面上时,摩擦力随单位水膜厚度的变化值达到500 N。因此汽车左右轮行驶在干燥和积水路面时,路表水膜厚度越大,行驶速度越大,发生侧滑的可能性就越高。
(3)采用侧转角指标定量地衡量车辆侧滑危险性,结果表明在无驾驶员操控情况下,汽车高速(>90 km/h)行驶在厚层积水路面上(水膜厚度为9~12 mm)时,1 s后汽车的相对侧转角差超过最佳控制角度(25°),此时汽车操纵性开始下降;2 s后汽车相对侧转角差已超过90°,车辆发生侧滑,易发生交通事故。
| [1] | 沙庆林. 高速公路沥青路面早期破坏现象及预防. 北京:人民交通出版社,2008. SHA Qing-lin. Premature Damage and Its Preservative Measures of Bituminous Pavement on Expressway.Beijing: China Communications Press, 2008. |
| [2] | 公安部交通管理局.中华人民共和国道路交通事故统计年报 (2010年度) [R]. 无锡:公安部交通管理科学研究所, 2011. Traffic Management Bureau of Ministry of Public Security. RoadTraffic Accident Statistics Annual Report of the People's Republic of China (2010)[R]. Wuxi: Traffic Management Research Institute of Ministry of Public Security, 2011. |
| [3] | ONGG P, FWA T F. Prediction of Wet-Pavement Skid Resistance and Hydroplaning Potential[J]. |
| [4] | FWAT F, KUMAR S S, ONG G P, et al. Analytical Modeling of Effectsof Rib Tires on Hydroplaning[J]. |
| [5] | ONGG P, FWA T F. Wet-pavement Hydroplaning Risk and Skid Resistance: Modeling[J]. |
| [6] | FWAT F, ONG G P. Wet-pavement Hydroplaning Risk and Skid Resistance: Analysis[J]. |
| [7] | 季天剑,黄晓明,刘清泉. 部分滑水对路面附着系数的影响[J]. 交通运输工程学报, 2003, 3(4): 10-12. JI Tian-jian, HUANG Xiao-ming, LIU Qing-quan. PartHydroplaning Effect on Pavement Friction Coefficient[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4), 10-12. |
| [8] | 季天剑,黄晓明,刘清泉,等. 道路表面水膜厚度预测模型[J]. 交通运输工程学报, 2004, 4(3): 1-3. JI Tian-jian, HUANG Xiao-ming, LIU Qing-quan, et al. Prediction Model of Rain Water Depth on Road Surface[J]. Journal of Traffic and Transportation Engineering, 2004, 4(3): 1-3. |
| [9] | 季天剑,高玉峰,陈荣生. 轿车轮胎动力滑水分析[J]. 交通运输工程学报, 2010, 10(5): 57-60. JI Tian-jian, GAO Yu-feng, CHEN Rong-sheng. Dynamic Hydroplaning Analysis of Car Tire[J]. Journal of Traffic and Transportation Engineering, 2010, 10(5): 57-60. |
| [10] | 徐进,彭其渊,邵毅明.直线路段积水路面车辆事故产生机理分析[J]. 中国公路学报, 2009, 22(1): 97-103. XU Jin, PENG Qi-yuan, SHAO Yi-ming. Mechanism Analysis of Vehicle Accident on Surface Gathered Water in Straight Sections[J]. China Journal of Highway and Transport, 2009, 22(1): 97-103. |
| [11] | 李长城, 刘小明, 荣建. 路面湿滑指数开发及其在交通运行管理中的应用[J]. 公路交通科技, 2010, 27(11): 132-136. LI Chang-cheng, LIU Xiao-ming, RONG Jian. Development of Pavement Slippery Index and Its Application in Traffic Operation Management[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 132-136. |
| [12] | 董斌,陈明磊,唐伯明,等. 基于FLUENT软件的雨天轮胎动水压强的影响因素研究[J]. 公路交通科技, 2012, 29(4): 120-125. DONG Bin, CHEN Ming-lei, TANG Bo-ming, et al. Influencing Factor of Hydrodynamic Pressure on Tire in Wet Weather Based on Fluent[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 120-125. |
| [13] | GILLESPIET D. 车辆动力学基础[M]. 赵六奇,金达锋, 译. 北京:清华大学出版社, 2006. GILLESPIET D. Fundamentals of Vehicle Dynamics [M]. ZHAO Liu-qi, JIN Da-feng, translated. Beijing: Tsinghua University Press, 2006. |
| [14] | 庄继德.汽车轮胎学[M]. 北京:北京理工大学出版社, 1999. ZHUANG Ji-de. Principles of Automobile Tire[M]. Beijing: Beijing Institute of Technology Press, 1999. |
| [15] | 董斌. 部分滑水条件下高速公路车辆行驶安全性研究. 重庆:重庆交通大学, 2011. DONG Bin.Study of Safety Driving on Expressway under Partly Hydroplaning . Chongqing: Chongqing Jiaotong University, 2011. |
 2014, Vol. 31
2014, Vol. 31
