扩展功能
文章信息
- 赵明华, 刘涛, 杨超炜, 尹平保, 赵衡
- ZHAO Ming-hua, LIU Tao, YANG Chao-wei, YIN Ping-bao, ZHAO Heng
- 考虑陡坡效应的横向受荷桩受力分析纽玛克解答
- Analysis on Mechanical Characteristics of Laterally Loaded Pile by Newmark Method Considering Steep Slope Effect
- 公路交通科技, 2014, 31(10): 58-64
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 58-64
- 10.3969/j.issn.1002-0268.2014.10.010
-
文章历史
- 收稿日期:2013-12-20
2. 长沙理工大学 土木与建筑学院, 湖南 长沙 410004;
3. 中南大学 资源与安全工程学院, 湖南 长沙 410083
2. School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha Hunan 410004, China;
3. School of Resources and Safety Engineering, Central South University, Changsha Hunan 410083, China
为保护现有的自然环境,在山区修建高速公路或铁路时,应避免大切大挖,从而某些路段不得不将桥梁基桩设置在边坡上[1]。在处于边坡上的桥梁基桩,一方面需承受桩顶横向荷载作用,另一方面还将承受坡体变形而产生的桩侧土压力,其与普通的水平受荷桩及常规的抗滑桩均不相同,属于特殊的横向受荷桩(桩顶及桩身均存在横向荷载作用)。
目前有关横向受荷桩的研究主要存在于水平受荷桩和抗滑桩等领域。在水平受荷桩方面,已有一些学者[2,3]对大变形条件下水平受荷单桩承载性状与受力特性进行研究;Pise等[4,5]探讨了地基土的成层性对水平受荷桩的内力与变形影响;苏静波等[6,7]基于p-y曲线法和NL法对水平受荷桩非线性受力特性进行有限元分析;史文清等[8]采用接触算法研究了桩土接触面特性对水平受荷桩受力特性的影响。然而,上述研究仅考虑桩顶水平荷载的作用,忽视了桩身横向荷载的影响。而在抗滑桩方面,戴自航等[9,10]基于地基系数m-k法原理,提出了抗滑桩内力计算的有限差分法;郑颖人等[11,12]利用有限元强度折减法及测斜数据反演法计算抗滑桩的内力与位移;宋从军等[13]根据埋入式抗滑桩位置设置的特点,对桩身内力进行分析计算。关于抗滑桩的研究通常只考虑桩侧岩土压力的作用,而忽视桩顶荷载的影响。对于陡坡段横向受荷桩,应综合考虑桩顶及桩侧横向荷载的共同作用。
为此,在现有研究的基础上,首先,分析陡坡效应的形成机理;其次,根据陡坡段横向受荷桩的受力特点,对桩侧横向荷载及土体抗力进行合理简化,建立考虑陡坡效应的简化计算模型;最后,通过纽玛克数值计算方法求得陡坡段横向受荷桩的桩身内力与位移。 1 陡坡效应分析
由于坡体的存在,陡坡段横向受荷桩的受力特性与平地基桩并不相同。边坡坡体形成的临空面,使边坡一侧不再是无限边界,因而桩身前后不再对称,桩前岩土体提供的水平抗力将会明显减小甚至完全消退,此即所谓的陡坡效应。
当基桩入土深度达到一定值时,陡坡效应对处于此深度以下的基桩的影响可以忽略不计,这时可将桩周土体视为完全对称,因而计算桩周土体水平抗力时,可将其视为平地基桩进行计算[14]。此边坡临空面的距离即为边坡稳定围岩厚度,计算时可简化认为与桩径d成正比,即D=nd,对应的基桩入土深度即为临界深度h0,计算式为h0=ndtanθ,式中θ为坡面的倾角,如图 1所示。对应临界深度h0以上的土体,由于边坡的存在,需考虑陡坡效应,故对地基抗力比例系数进行适当调整,假定其随深度线性变化,即令m= m0z/h0,式中m0为土体初始的抗力比例系数,z为坡面以下某点的竖向深度值,且0≤z≤h0。对于临界深度h0以下的土体,其地基抗力比例系数取为初值m0。
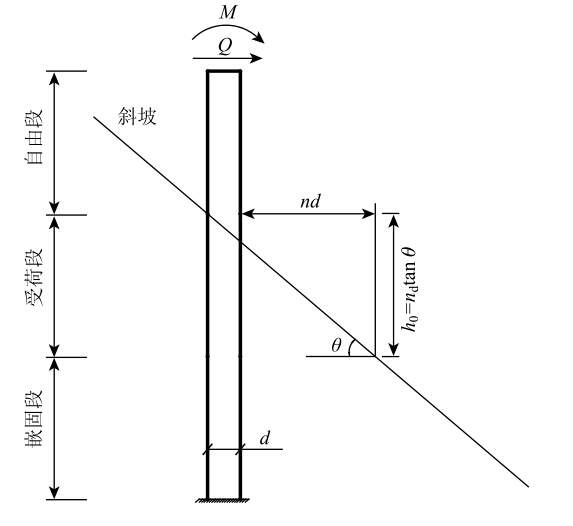
|
| 图 1 陡坡效应分析图 Fig. 1 Analysis diagram of steep slope effect |
(1) 由文献[15]可知,桩周横向荷载有多种分布形式,为方便计算,本文假定其呈三角形分布;
(2) 根据大量资料以及现场实测数据[14,16]分析表明,斜坡距桩身水平距离为3~5倍桩径范围内的土体,即n取值为3~5时,应考虑陡坡效应,对地基抗力比例系数m进行适当假定计算;
(3) 依据Winkler弹性地基梁理论,将地基土体视为相互独立的弹簧支座,以弹簧支承力表示桩周土体抗力,其值与桩身任意一点的位移成正比。
综合上述,可建立基桩简化受力模型,如图 2所示。
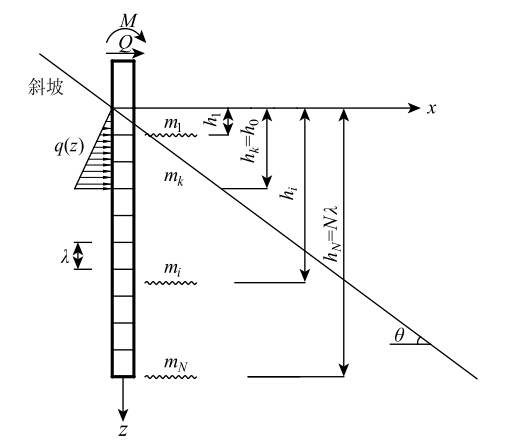
|
| 图 2 陡坡段横向受荷桩简化受力模型 Fig. 2 Simplified mechanical model of laterally loaded pile in steep slope |
根据基本假定,建立的陡坡上桥梁基桩计算模型如图 3所示,图中M,Q分别为桩顶所受的弯矩与横向荷载;Mi、Qi分别表示第i节点处的等效弯矩与剪力,取值为i=0,1,2,…,k;Ki为第i节点处的弹簧刚度,取值为i=0,1,2,…,N。
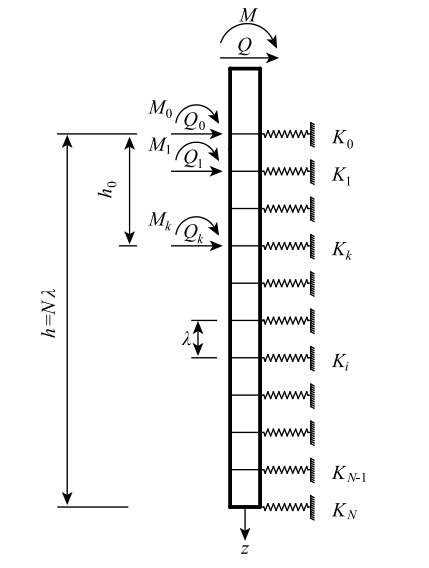
|
| 图 3 陡坡段横向受荷桩计算模型 Fig. 3 Computational model of laterally loaded pile in steep slope |
纽玛克法的基本思路是根据计算精度需要,将桩身划分为若干段,以桩节点处等效弹簧支承力表示桩周土体抗力,通过递推运算求解桩身内力与位移。 2.2.1 节点弹簧刚度系数的计算
如图 3所示,假定坡面以下桩身长度为h,对坡面距桩身水平距离为4倍桩径范围内的土体考虑陡坡效应,即取n=4,因此h0=4d tanθ,根据文克尔假定,将地基视为若干个支承弹簧,为了计算方便,将桩身等分为若干微段,每一微段长λ,则h0深度范围内可将桩身分为k=h0/λ个微段,整个桩身可分为N=h/λ个微段。
由文献[1]可知坡面以下深度z处的地基抗力系数为:
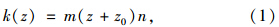
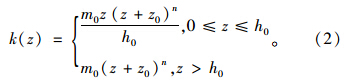
弹簧刚度系数为:
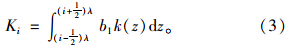
将式(2)代入式(3),并分别对不同深度的基桩微段进行积分,可以得出坡面处即节点序号为i=0 的支承点弹簧刚度系数为:
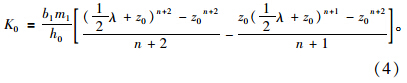
坡面与距坡面深度为h0范围之间,即当节点序号0<i<k时各支承点的弹簧刚度系数为:
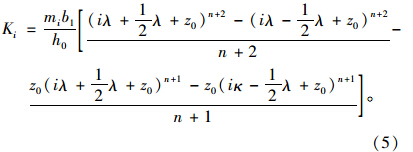
距坡面深度为h0处即节点序号i=k的支承点弹簧刚度系数为:
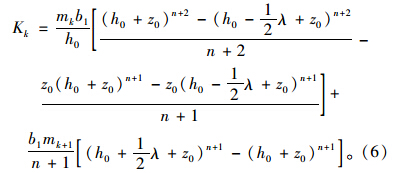
距坡面深度h0与桩底之间,即节点序号k<i<N时各支承点的弹簧刚度系数为:
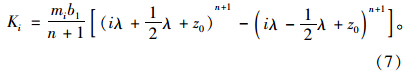
桩底位置即节点i=N的支承点弹簧刚度系数为:
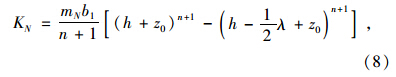
2.2.2 等效节点荷载计算
根据上述分析,基桩微段受荷如图 4所示。
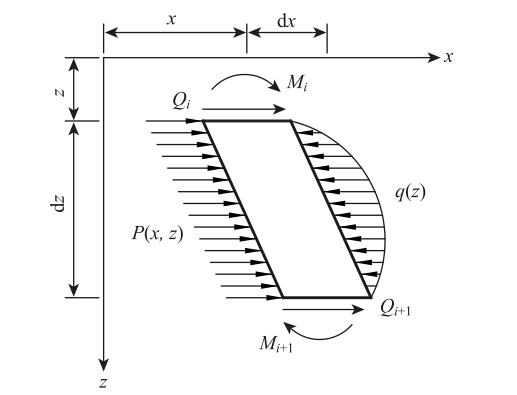
|
| 图 4 基桩微段受力分析图 Fig. 4 Analysis diagram of element of pile |
桩侧作用的荷载表示为qi,利用结构力学知识,将作用在基桩微元上的分布荷载转化为等效节点荷载,如图 4所示,则可得坡面处即i=0时,等效节点荷载:
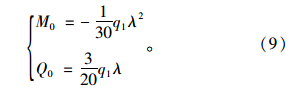
坡面以下与距坡面深度h0之间,即1≤i<k时,各点的等效节点荷载为:
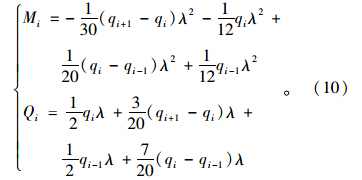
距坡面深度为h0,即i=k时,其等效节点荷载为:
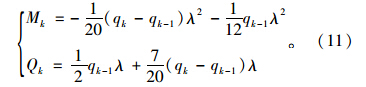
距坡面深度为h0以下到桩底位置处,即k<i≤N时,各点的等效节点荷载为:

以上各式中,M0,Q0,Mk,Qk,Mi,Qi分别为节点0,k,i位置处的等效弯矩与剪力;q1,qk-1,qk,qi-1,qi和qi+1分别为节点1,k-1,k,i-1,i和i+1位置处的作用的荷载。 2.2.3 纽玛克法解答
(1)假定桩底位移x1N=0,转角φN1=0,在外荷载作用下求出各桩节点处位移xi1。
设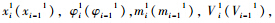
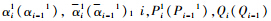 分别为第i(i-1)个节点处桩身的位移、转角、弯矩、剪力、虚荷载、等效集中虚荷载、弹簧支座支承力和外荷载;Mi-1,Ki-1分别表示外弯矩和弹簧支座的刚度系数;m1k,V1k,α1k,k1,Qk分别表示第k个节点处桩身的弯矩、剪力、虚荷载、等效集中虚荷载和外荷载;αk-11,αi-21,α10,α11分别为第(k-1)、第(i-2),第0和第1节点处桩身的虚荷载;10表示第0节点(坡面处)桩身的等效集中虚荷载。所有符号的上标“1”表示第一个递推过程。
分别为第i(i-1)个节点处桩身的位移、转角、弯矩、剪力、虚荷载、等效集中虚荷载、弹簧支座支承力和外荷载;Mi-1,Ki-1分别表示外弯矩和弹簧支座的刚度系数;m1k,V1k,α1k,k1,Qk分别表示第k个节点处桩身的弯矩、剪力、虚荷载、等效集中虚荷载和外荷载;αk-11,αi-21,α10,α11分别为第(k-1)、第(i-2),第0和第1节点处桩身的虚荷载;10表示第0节点(坡面处)桩身的等效集中虚荷载。所有符号的上标“1”表示第一个递推过程。
具体递推运算过程如下:
当k<i≤N时,
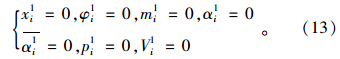
当i=k时,
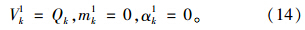
当1≤i<k时,
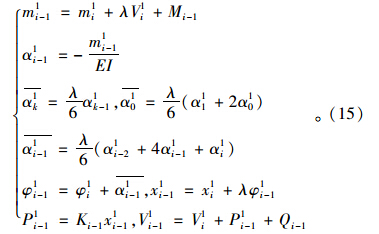
上述递推由桩底推算至坡面的桩身位置处,通过以上递推式,可以求得坡面处桩的弯矩m10,转角φ10,剪力V10以及各节点处位移x1i。
(2) 假定桩底位移x2N=1,转角φ2N=0,在无荷载作用下求出各桩节点处位移x2i。
当i=N时,
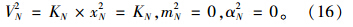
当1≤i≤N时,
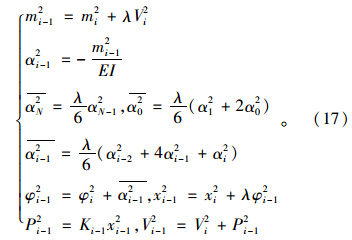
式(16)、(17)中,m2N,V2N,α2N,2N和KN分别为第N节点(桩底处)桩身的弯矩、剪力、虚荷载、等效集中虚荷载和弹簧支座的刚度系数,其余各物理量的意义同上,所有符号的上标“2”表示第二个递推过程。通过以上递推式,可以求得坡面处桩的弯矩m20,转角φ20,剪力V20以及各节点处位移x2i。
(c) 假定桩底位移x3N=0,转角φ3N=1,在无荷载作用下求出各桩节点处位移x3i。
当i=N时,
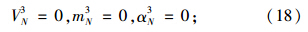
根据坡面处桩身顶部边界条件可建立相应的方程组:
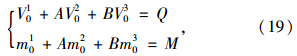
将式(19)计算出来的比例系数A和B回代后,即可得到修正后各支承点实际位移Xi,剪力Vi及弯矩Mi。
当0≤i<N时,
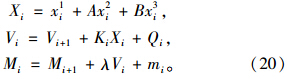
当i=N时,
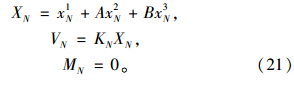
综合以上,纽玛克法计算基桩内力与位移的具体计算步骤如下:
(1) 根据基桩受力特点,将坡面以下桩身划分为N个单元;由文克尔假定,将地基视为若干个支承弹簧,弹簧个数N等于所划分单元个数;
(2) 分别计算各单元支承点的弹簧刚度系数Ki以及等效节点荷载;
(3) 假定桩底位移和转角均为0,即x1N=0,φ1N=0,在外荷载作用下求出坡面处桩身弯矩m10,转角φ10,剪力V10及各弹簧支承点位移x1i;
(4) 假定桩底位移为1,转角为0,即x2N=1,φ2N=0,在无荷载作用下求出坡面处桩身弯矩m20,转角φ20,剪力V20及各弹簧支承点位移x2i;
(5) 假定桩底位移为0,转角为1,即x3N=0,φ3N=1,在无荷载作用下求出坡面处桩身弯矩m30,转角φ30,剪力V30及各弹簧支承点位移x3i;
(6) 根据坡面处桩身边界条件建立二元线性代数方程:
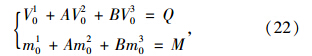
(7) 将比例系数A和B回代,计算各支承点实际位移Xi,剪力Vi及弯矩Mi。
具体计算流程如图 5所示。
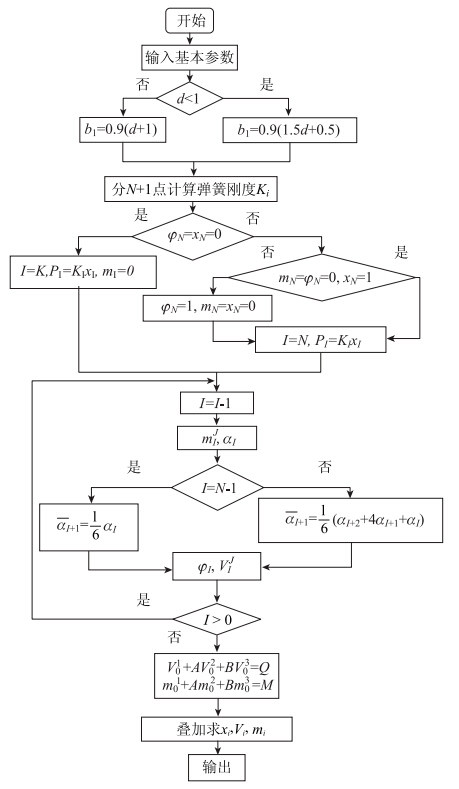
|
| 图 5 纽玛克法求解流程图 Fig. 5 Flowchart of solving by Newmark method |
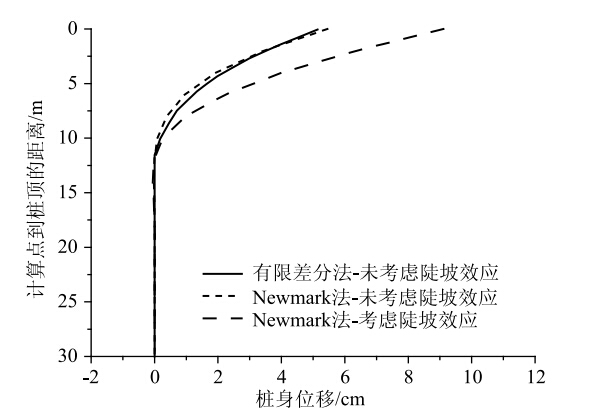
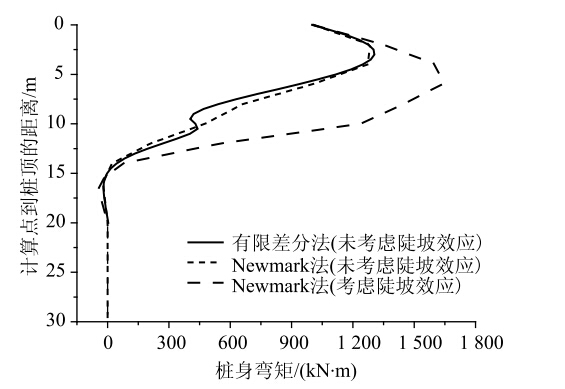
为验证本文计算方法的可行性,采用文献[17]中的算例进行计算验证。某斜坡上的一桥梁基桩,桩径2 m,桩长30 m,其自由段、受荷段、嵌固段分别为l1=0 m,l2=10 m,l3=20 m;桩身重度γ=25 kN/m;混凝土弹性模量Ep=18 GPa;受荷段和嵌固段地基抗力比例系数m1=5 000 kN/m4、m2=50 000 kN/m4;作用在桩顶水平荷载、偏心弯矩分别为170 kN和1 000 kN·m;桩侧横向荷载合力为500 kN;地面处与土黏聚力有关的系数z0为零。计算时对斜坡距桩身水平距离为4倍桩径范围内土体的地基抗力进行折减,即取n=4,故临界深度h0=4dtanθ,本例中θ取为30°。地基抗力系数 k(z)=m(z+z0)n中取n=1, 即采用m法进行计算。根据自编的Matlab程序计算得到桩身水平位移及桩身弯矩如图 6和图 7所示。
|
| 图 6 桩身位移计算结果对比 Fig. 6 Comparison of calculated displacements of pile |
|
| 图 7 桩身内力计算结果对比 Fig. 7 Comparison of calculated internal forces of pile |
由图 6、图 7及表 1可知,本文计算结果与文献值吻合较好。在未考虑陡坡效应的情况下,桩身水平位移及桩身弯矩曲线均与有限差分法计算结果非常接近,桩顶水平位移误差为3.8%;桩身最大弯矩误差为1.5%。由此可见,本文计算方法及程序是合理可行的。另外,在考虑陡坡效应时,由于对陡坡段桩侧土体抗力进行了折减,因此所得桩身水平位移及桩身最大弯矩值比未考虑陡坡效应时均明显增大,即考虑陡坡效应对工程安全性有利。
| 项目 | 文献值 | 本文值 | 计算误差/% |
| 桩顶水平位移/cm | 5.24 | 5.45 | 3.8 |
| 桩身最大弯矩/(kN·m-1) | 1 304.9 | 1 285.11 | 1.5 |
(1) 分析了陡坡效应的形成机理及陡坡段横向 受荷桩的受力特性,合理简化了桩周横向荷载以及岩土体抗力;基于Winkler弹性地基梁理论,建立了考虑陡坡效应的横向受荷桩的简化受力模型。
(2) 采用纽玛克数值计算方法进行递推运算得到桩身内力与位移,并与某实际工程进行对比分析发现:桩身最大弯矩及水平位移最大误差均不超过5%,验证了本文计算方法及程序的可行性。
(3) 考虑陡坡效应后,对斜坡距桩身水平距离为4倍桩径范围内土体的地基抗力进行折减,故得到的计算结果偏大,对工程安全性有利。
| [1] | 赵明华. 桥梁桩基计算与检测 [M]. 北京: 人民交通出版社, 2000. ZHAO Ming-hua. Calculation and Detection for Pile Foundations of Bridges [M]. Beijing: China Commun-ications Press, 2000. |
| [2] | 赵明华, 汪优, 黄靓. 水平受荷桩的非线性无网格法分析 [J]. 岩土工程学报, 2007, 29(6): 907-912. ZHAO Ming-hua, WANG You, HUANG Liang. Nonlinear Analysis of Meshless Method for Piles under Horizontal Load [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 907-912. |
| [3] | 张磊, 龚晓南, 俞建霖. 大变形条件下单桩水平承载性状分析 [J]. 土木建筑与环境工程, 2013, 35(2):61-65. ZHANG Lei, GONG Xiao-nan, YU Jian-lin. Behavior Analysis of Lataerlly Loaded Single Pile under Large Deflection [J]. Journal of Civil, Architectural & Environmental Engineering, 2013,35(2):61-65. |
| [4] | PISE P J. Laterally Loaded Piles in a Two-layer Soil System [J]. Journal of the Geotechnical Engineering Division, 1982, 108(9): 1177-1181. |
| [5] | YANG Z, JEREMIC B. Study of Soil Layering Effects on Lateral Loading Behavior of Piles [J]. |
| [6] | 苏静波, 邵国建, 刘宁. 基于p-y曲线法的水平受荷桩非线性有限元分析 [J]. 岩土力学, 2006, 27(10): 1781-1785. SU Jing-bo, SHAO Guo-jian, LIU Ning. Nonlinear Finite Element Analysis of Piles under Lateral Load Based on p-y Curves [J]. Rock and Soil Mechanics, 2006, 27(10): 1781-1785. |
| [7] | 吴峰, 时蓓玲. 基于NL法的水平受荷桩非线性有限元分析 [J]. 水运工程, 2007(12): 9-12. WU Feng, SHI Bei-ling. Nonlinear Finite Element Analysis of Piles under Lateral Load Based on NL Method [J]. Port & Waterway Engineering, 2007(12): 9-12. |
| [8] | 史文清, 王建华, 陈锦剑. 考虑桩土接触面特性的水平受荷单桩数值分析 [J]. 上海交通大学学报, 2006, 40(8):1457-1461. SHI Wen-qing, WANG Jian-hua, CHEN Jin-jian. Numerical Analysis of the Laterally Loaded Pile Considering the Unlinear Characteristic of Pile-soil Interface [J]. Journal of Shanghai Jiaotong University, 2006, 40(8): 1457-1461. |
| [9] | 戴自航, 彭振斌. 抗滑桩全桩内力计算 "m-k"法的有限差分法 [J]. 岩土力学, 2002, 23(3):321-325. DAI Zi-hang , PEN Zhen-bin. Finite Difference Method Based on "m-k" Method for Calculation of Internal Forces of a Whole Stabilizing Pile [J]. Rock and Soil Mechanics, 2002, 23 (3):321-325. |
| [10] | 杨佑发. 弹性抗滑桩内力计算的有限差分"m-k"法 [J]. 重庆建筑大学学报, 2002, 24(1): 13-18. YANG You-fa. Finite Difference "m-k" Method of Calculation of Anchor-stabilizing Piles[J]. Journal of Chongqing Jianzhu University, 2002, 24(1): 13-18. |
| [11] | 郑颖人, 雷文杰, 赵尚毅, 等. 抗滑桩设计中的两个问题 [J]. 公路交通科技, 2005, 22(6): 45-51. ZHENG Ying-ren, LEI Wen-jie, ZHAO Shang-yi, et al. Two Problems in Design Methods of Anti-slide Piles [J]. Journal of Highway and Transportation Research and Development, 2005, 22(6):45-51. |
| [12] | 申永江, 孙红月, 尚岳全, 等. 基于测斜数据的抗滑桩工作状态评价 [J]. 岩石力学与工程学报, 2009, 28(2):3591-3596. SHEN Yong-jiang, SUN Hong-yue, SHANG Yue-quan, et al. Evaluation of State of Anti-slide Piles Based on Inclinometer Data [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2):3591-3596. |
| [13] | 宋从军, 周德培, 肖世国. 岩石高边坡埋入式抗滑桩的内力计算 [J]. 岩石力学与工程学报, 2005, 24(1):105-109. SONG Cong-jun, ZHOU De-pei, XIAO Shi-guo. Calculation of internal Force of Embedded Anti-slide Pile in High Rock Slope [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1):105-109. |
| [14] | 杨明辉. 岩质陡坡桥梁桩基承载机理及其分析方法研究 [D].长沙: 湖南大学, 2006. YANG Ming-hui. Load Mechanics and Analysis Method for Rock Steep Slope Bridge Piles [D]. Changsha: Hunan University, 2006. |
| [15] | 戴自航. 抗滑桩滑坡推力和桩前滑体抗力分布规律的研究 [J].岩石力学与工程学报, 2002, 21(4): 517-521. DAI Zi-hang. Study on Distribution Laws of Landslide-Thrust and Resistance of Sliding Mass Acting on Antislide Piles [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 517-521. |
| [16] | 赵明华, 邹新军, 罗松南, 等. 横向受荷桩桩侧土体位移应力分布弹性解 [J]. 岩土工程学报, 2004, 26(6): 767-771. ZHAO Ming-hua, ZOU Xin-jun, LUO Song-nan, et al. Elastic Analytic Solution to the Displacement and Stress Distribution in the Soil around Laterally Loaded Piles [J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 767-771. |
| [17] | ZHAO Ming-hua, LIU Jian-hua, LIU Dai-quan, et al. Force Analysis of Pile Foundation in Rock Slope Based on Upper-bound Theorem of Limit [J]. |
 2014, Vol. 31
2014, Vol. 31
