扩展功能
文章信息
- 武崇福, 赵宇
- WU Chong-fu, ZHAO Yu
- 基于厚板理论确定岩溶及采空区路基岩层顶板安全厚度
- Determining Safe Thickness of Subgrade Roof in Karst and Mined-out Area Based on Thick Plate Theory
- 公路交通科技, 2014, 31(10): 32-37
- Journal of Highway and Transportation Research and Denelopment, 2014, 31(10): 32-37
- 10.3969/j.issn.1002-0268.2014.10.006
-
文章历史
- 收稿日期:2013-4-23
随着高速公路的快速发展,一些路段不可避免地需要穿越岩溶及采空区。因此,作为影响顶板稳定性主要因素的顶板安全厚度问题,就成为了高速公路建设成败的关键问题,引起了工程和科研界的高度重视。
目前,国内外学者对顶板安全厚度的确定进行了大量的研究,制订了多种顶板安全厚度的计算方法,总体上可以分为数值分析法、模型预测法、解析法、半定量法等[1,2,3,4,5]。 数值分析方法,采用解的不收敛性作为破坏标准,其物理意义不是十分明确,并且由于计算整体模型参数的不确定性和复杂性,在多种情况下计算结果不能直接应用到实际工程中[6,7]。
模型预测方法是通过采集大量的试验和监测数据,对其进行科学的统计分析,确定采空区顶板破坏的临界厚度,但是该方法具有很强的针对性,对其在工程应用中的推广造成了很大的困难。
解析法通过最简单的符号运算来表达力学模型中的各个参数之间的相互关系,但往往会造成计算公式繁琐,求解需编程反复迭代,有时甚至不收敛,难以在工程中推广应用。
传统的半定量分析法主要分为[8]:荷载传递线交汇法、厚跨比法、按剪切概念估算法、按梁板受力情况估算法、洞穴顶板坍塌堵塞估算法、按破裂拱概念估算法。
根据上述传统的半定量分析法,按文献[8]所述,按5 m厚的覆土考虑对岩溶及采空区顶板安全厚度进行估算,结果如表 1所示。
|
空洞大小 b×h/m2 | 1×1 | 2×2 | 3×3 | 4×4 | 5×5 | 6×6 | 7×7 |
| 荷载传递交汇法 | 0.71 | 1.43 | 2.15 | 2.86 | 3.58 | 4.28 | 5.00 |
| 厚跨比法 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| 按剪切模量估计 | 0.02 | 0.06 | 0.12 | 0.24 | 0.45 | 0.66 | 0.89 |
| 按梁板受力估算 | 0.16 | 0.39 | 0.72 | 1.16 | 1.78 | 2.37 | 2.97 |
| 按坍塌堵塞概念估算 | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 |
| 按破裂拱估算 | 1.42 | 2.84 | 4.26 | 5.68 | 7.10 | 8.52 | 9.94 |
从表 1中可以看出,各种半定量方法的计算结果相差很大,其力学模型的适用性存在疑问。特别是当顶板较厚时,即当厚跨比e>0.2时,按薄梁板抗弯估算,忽视了板的剪切变形,造成其力学机理不明确。因此,迫切需要开辟一条新的途径,建立岩溶及采空区岩层顶板安全厚度的确定方法,这正是本文的核心研究内容。
本文在深入分析研究岩溶及采空区岩层顶板安全厚度影响因素及岩溶岩层顶板安全厚度传统半定量分析方法所存在缺陷的基础上,基于Reissner厚板理论,在求解过程中结合加权余量法,在四边固支与四边简支的情况下,考虑顶板上部受到均布荷载作用,推导了均布荷载作用下顶板的挠度方程和内力表达式,公式比较简单,便于工程应用。以岩层的拉应力为控制条件,结合文献[9]推导出的顶板安全厚度计算公式,进行顶板变形与受力分析。最后,结合实际工程实例,对顶板安全厚度进行了验证分析。 1 力学简化模型及公式推导
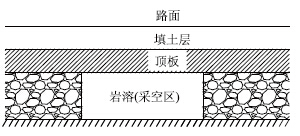
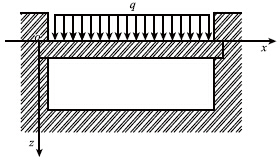
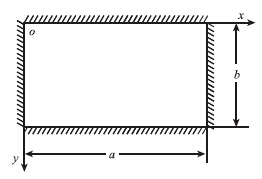
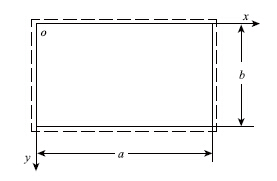
岩溶及采空区的几何区域近似地简化成为矩形区域,如图 1、图 2所示。根据顶部岩体边界处的裂纹情况,当不出现裂纹时,视边界条件为固定条件下的弹性矩形厚板,如图 3所示;随着板块尺寸的增大,顶板的长边中点(a/2,0) 、(a/2,b)先进入塑性状态,而后沿长边扩展形成塑性铰;紧接着,顶板的短边中点(0,b/2)、(a,b/2)也进入塑性状态,也沿边界扩展形成塑性铰;最后四个边界全部成为可以自由转动的铰支边界,边界条件由固定支承变成了简支。此时,顶板只是边界约束减弱了,但是整体并没有破坏[10],如图 4所示。建立坐标系xoy,设弹性矩形厚板长边为a,短边为b,板厚为h。厚板的物理力学参数值取岩体物理参数值,假定岩体的弹性模量为E,泊松比为υ,体密度为ρ,抗拉强度极限为σs,设上层岩土介质对顶板上表面的压力为均布载荷q。
|
| 图1 岩溶及采空区垂直剖面图 Fig.1 Vertical section of karst and mined-out area |
|
| 图2 简化模型 Fig.2 simplified model |
|
| 图3 四边固支板模型 Fig.3 Model of 4-side fixed plates |
|
| 图4 四边简支板模型 Fig.4 Model of 4-side simply supported plates |
基于Reissner厚板理论的静力学问题基本方程为[11]
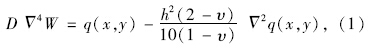
式中,D为板的抗弯刚度,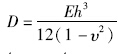 ; Δ 4为双调和算子,
; Δ 4为双调和算子, ; w为板的挠曲面; q(x,y)为作用在板上的荷载,可由岩土层对顶板的均布压力载荷q0与其自重载荷ρgh叠加而成,即q=q0+ρgh。由Reissner厚板理论,可以推导出板的弯矩、剪切力和转角公式为
; w为板的挠曲面; q(x,y)为作用在板上的荷载,可由岩土层对顶板的均布压力载荷q0与其自重载荷ρgh叠加而成,即q=q0+ρgh。由Reissner厚板理论,可以推导出板的弯矩、剪切力和转角公式为
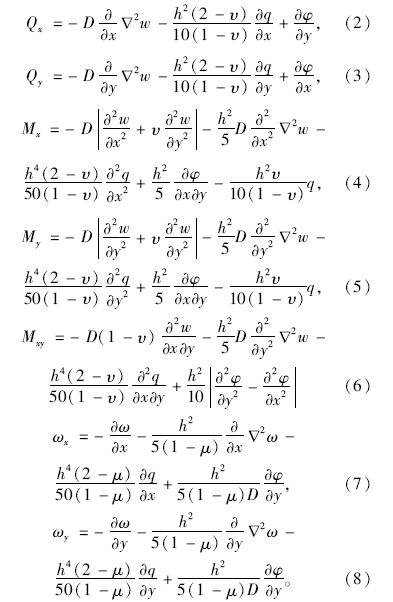
由于岩溶及采空区顶板在发生破坏时,四周的边界条件不同,造成了函数的表达式不同,所以需要分别对其进行推导计算。
顶板在破坏前的边界条件为四边固定[10],即:
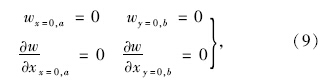
所以根据边界条件,选取试函数满足上述边界条件,即取:
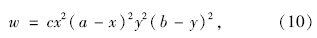
将式(10)代入方程(1)的伽辽金弱形式方程[12],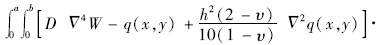
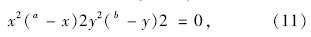
将荷载展开成双三角级数形式,即:
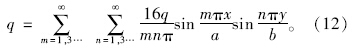
在保证精度的条件下为了简化计算,可近似的取前两项,则式(12)为
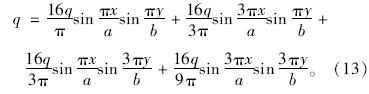
将式(13)带入式(11)中,用Matlab求解并略去高阶项得:
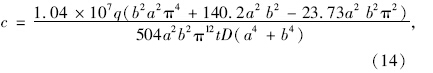
式中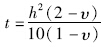
将式(14)代入式(10)并化简可得到顶板的挠度函数式:
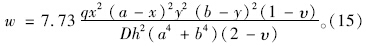
顶板在破坏前的边界条件为四边简支,即:
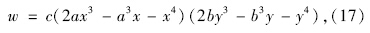
所以根据边界条件,选取试函数满足上述边界条件,即取:
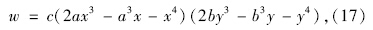
将式(13)、(17)代入式(11)用Matlab求解并略去高阶项得:
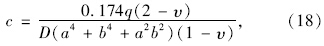
将式(18)代入(17)并化简即得到顶板的挠度函数式:
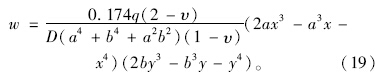
假定应力函数为[13]:
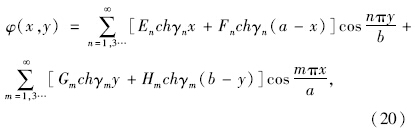
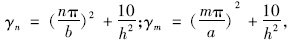
将式(10)、(15)和式(17)、(19)分别代入式(7)、(8)中,再由固支与简支相同的边界条件
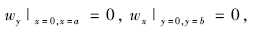 可得En=0,Fn=0,Gm=0,Hm=0。
可得En=0,Fn=0,Gm=0,Hm=0。
因此,应力函数为

四边固支条件下:
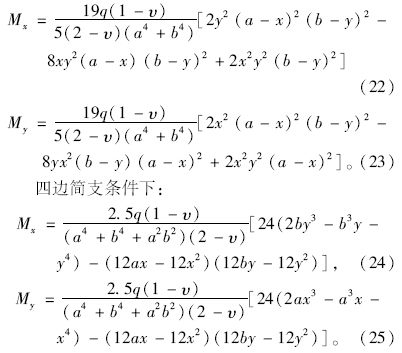
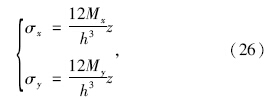
根据上述应力函数式,弹性板拉应力最大值出现在板底位置,切应力最大值出现在板表面处,即Z=0处。
岩石的压应力强度大于拉应力强度,为了保证顶板的稳定性,以拉应力极限强度为控制条件。即当顶板下表面达到拉应力最大值时发生失稳破坏,采用文献[9]的计算方法,则其顶板安全厚度应满足:
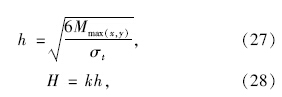
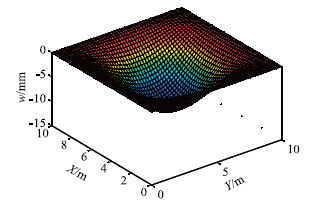
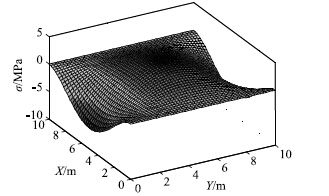
假定顶板上作用均布荷载值为1 000 kN/m2,顶板层为页岩,重度为26.5 kN/m3,顶板厚度为2 m,弹性模量为2 200 MPa,泊松比为0.3,极限抗拉强度为0.2 MPa,极限抗压强度为50 MPa,弹性厚板边长10 m×10 m。 将相关参数代入上述求解方法求得四边固支条件下的挠度曲面如图 5所示,x方向的拉应力曲面如图 6所示,图中最大挠度值为9.96 mm,最大弯矩为4 889.7 kN·m。
|
| 图5 四边固支条件下顶板挠度曲面 Fig.5 Deflection curve surface of 4-side fixed roof |
|
| 图6 四边固支条件下顶板拉应力曲面 Fig.6 Tensile stress curve surface of 4-side fixed roof |
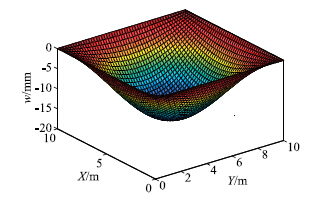
同理将相关参数代入上述求解方法得四边简支条件下的挠度曲面如图 7所示,x方向的拉应力曲面如图 8所示,图中最大挠度值为17 mm,最大弯矩为13 674 kN·m。
|
| 图7 四边简支条件下顶板挠度曲面 Fig.7 Deflection curve surface of 4-side simply supported roof |
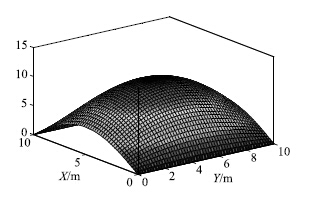
|
| 图8 四边简支条件下顶板拉应力曲面 Fig.8 Tensile curve surface of 4-side simply supported roof |
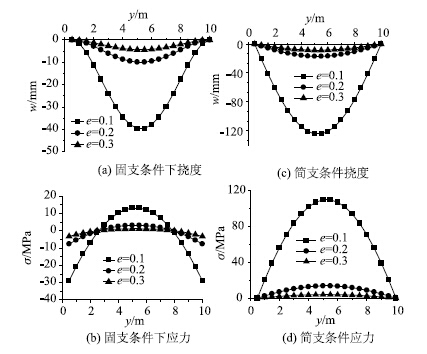
由图 9可知:
|
| 图9 顶板挠度和内力随厚跨比的变化曲线 Fig.9 Curves of deflection and internal force of roof varying with thickness-span ratio |
(1)顶板厚跨比对其挠度与应力影响显著,尤其在e减小到0.1时,挠度与应力的分布曲线变化较大。
(2)顶板挠度关于中心位置对称分布,并在中心处取得最大值。厚跨比越大,挠度越小。
(3)顶板应力关于中心位置对称分布,最大拉应力出现在板的中心位置,随着厚跨比的增大顶板各处应力值均逐渐减小。
(4)相同受力条件下四边简支比四边固支的矩形厚板,产生的挠度与拉应力数值大。 3 应用实例
国道主干线湘潭至邵阳高速公路,穿过众多的岩溶及采空区,严重影响了高速公路路基的稳定性。需要对岩溶及采空区进行处理,而岩溶及采空区岩层顶板安全厚度是其处理的基本依据[8]。
通过勘察测量得知潭邵高速公路绝大多数溶洞尺寸为3 m×3 m×3 m,顶板岩性以页岩为主,其极限抗压强度约为50 MPa,抗拉极限强度约为0.2 MPa,顶板上层填土层厚以1 m为主,并且顶板四周没有发现裂纹,所以边界条件以固支为主。计算荷载为自重荷载与行车荷载之和,其中行车荷载按设计轮载和设计轴载计算,并且考虑到车辆的增加和超限车辆等因素的影响,以2倍的设计值进行计算。行车荷载假定上面作用有300 kN级消防车,并且已知后轴轮压P=60 kN,轮压着地面积为0.2 m×0.6 m,动力系数为1.3,故可取行车荷载为38 kN/m2,自重荷载为20 kN/m2。将上述荷载代入式(20)~(28)中计算得H=1.77 m,取H=2 m。 4 结论
(1)基于Reissner 厚板理论,并在求解过程中结合加权余量法,概化了岩溶及采空区顶板的力学模型,以四边固定和四边铰接为边界条件,推导出均布荷载作用下岩溶及采空区顶板挠度的解析表达式。
(2)顶板上方均布荷载作用下,随着顶板厚跨比的不断变化,顶板挠度和拉应力也呈现出显著变化特点。并且随厚跨比的增大,顶板的挠度减小速率要大于拉应力减小速率。
(3)以顶板岩层抗拉强度为控制条件,结合文献[9]采用的的顶板安全厚度计算公式,运用到实际工程中进行验证分析,能够取得明显的经济效益,对类似工程实践具有借鉴和指导意义。
本论文提出的计算方法适用于在均布荷载下,采空区上方岩体厚度变化不大,并且岩层形状规则的弹性矩形厚板。对于非均布荷载状况,或岩层有一定倾角的状况有待进一步研究,并且在工程中加以验证。
| [1] | 田志恒,聂永祥. 复杂采空区顶板最小安全厚度的确定方法.采矿技术,2009,(5):26-27. TIANZhi-heng,NIE Yong-xiang. Determination Method of Minimum Safety Thickness of Roof in Complicated Mined-out Regions. Mining Technology, 2009, 9(5): 26-27. |
| [2] | 蒋冲,赵明华,胡柏学,等. 路基溶洞顶板稳定性影响因素分析. 公路工程,2009,34(1):5-9. JIANG Chong, ZHAO Ming-hua, HU Bo-xue, et al. Stability Factors Analysis for Subgrade Karst Roof. Highway Engineering, 2009,34(1):5-9. |
| [3] | PALEI S K, DAS S K. Logistic Regression Model for Prediction of Roof Fall Risks in Bord and Pillar Workings in Coal Mines. |
| [4] | SWIFT G, REDDISH D J. Stability Problems Associated with an Abandoned Ironstone Mine. |
| [5] | 交通部第二公路勘察设计院. 公路设计手册(路基).第二版.北京:人民交通出版社,1996. Second Highway Survey and Design Institute of MOT. Highway Design Manual (Subgrade). 2nd ed. Beijing:China Communications Press,1996. |
| [6] | 黎斌,范秋雁,秦凤荣. 岩溶地区溶洞顶板稳定性分析. 岩石力学与工程学报,2002,21(4):532-536. LI Bin, FAN Qiu-yan, QIN Feng-rong. Analysis on Roof Stability of Karst Cave in Karst Areas. Chinese Journal of Rock Mechanics and Engineering, 2002,21(4):532-536. |
| [7] | 曹文贵,程晔,赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究. 岩土工程学报,2005,27(6):621-625. CAO Wen-gui ,CHENG Ye, ZHAO Ming-hua. Studies on Numerical Manifold Method for Determination of Safe Thickness of Karst Roof in Roadbed. Chinese Journal of Geotechnical Engineering,2005,27(6):621-625. |
| [8] | 廖春芳,彭衡和,曹文贵,等. 岩溶及采空区路基岩层顶板安全厚度确定方法研究. 公路,2003(1):2-5. LIAO Chun-fang,PENG Heng-he, CAO Wen-gui,et al. Research on Determination Method of Safety Thickness of Top Slab of Rock Bedding of Subgrade in Karst and Mined-out Region.Highway,2003(1):2-5. |
| [9] | 王树仁,贾会会,武崇福. 动荷载作用下采空区顶板安全厚度确定方法及其工程应用.煤炭学报, 2010(8):1263-1268. WANG Shu-ren, JIA Hui-hui, WU Chong-fu.Determination Method of Roof Safety Thickness in the Mined-out Regions under Dynamic Loading and Its Application.Journal of China Coal Society, 2010(8): 1263-1268. |
| [10] | 贺广零. 基于厚板理论的水平煤层顶板临界厚度的分析. 地下空间与工程学报,2009,5(4):659-663,674. HE Guang-ling. Determination of Critical Thickness of Stiff Roof in Coal Mine Based on Thick Plate Theory.Chinese Journal of Underground Space and Engineering, 2009,5(4):659-663, 674. |
| [11] | 李文兰,付宝连,杨志安. 弹性地基上厚矩形板弯曲问题的边界积分法. 天津大学学报,1999(1):90-94. LI Wen-lan, FU Bao-lian,YANG Zhi-an. The Boundary Integral Method of the Bending Thick Rectangular Plates with Simple Supported All Four Edges on Elastic Foundation. Journal of Tianjin University,1999(1):90-94. |
| [12] | 冯果忱,郐继福.有限元模型综述:各类模型的力学背景及其有关数学问题. 固体力学学报,1980(1):123-138. FENG Guo-chen, KUAI Ji-fu. Summary of the Finite Element Model:Mechanical Background and Related Mathematical Problems of Various Models. Chinese Journal of Solid Mechanics, 1980(1):123-138. |
| [13] | 付宝连,谭文锋. 求解厚矩形板弯曲问题的功的互等定理法. 应用数学和力学,1995(4):367-379. FU Bao-lian, TAN Wen-feng. Reciprocal Theorem Method for Solving the Problems of Bending of Thick Rectangular Plates.Applied Mathematics and Mechanics, 1995(4):367-379. |
| [14] | 李欣业,付宝连,陈英杰. 功的互等定理在四边固定厚矩形板弯曲问题中的应用. 河北工业大学学报,1997(2):82-89. LI Xin-ye, FU Bao-lian, CHEN Ying-jie. A New Method for Solving the Problem of Bending of Thick Rectangular Plate with Four Edges Fixed by Using Reciprocal Theorem. Journal of Hebei University of Technology, 1997 (2): 82-89. |
 2014, Vol. 31
2014, Vol. 31
