扩展功能
文章信息
- 冯涛, 查伟雄, 严利鑫
- FENG Tao, ZHA Wei-xiong, YAN Li-xin
- 地铁运营中断下应急公交线路开行方案研究
- Study on Scheme of Emergency Bus Line Operation under Subway Operation Interruption
- 公路交通科技, 2021, 38(12): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(12): 152-158
- 10.3969/j.issn.1002-0268.2021.12.018
-
文章历史
- 收稿日期: 2020-09-13
地铁在运营期间发生突发中断事件,不仅会打破本区段的运营秩序,而且还会将这种影响传播至轨道交通网络,甚至会造成整个城市的公共交通系统紊乱。因此,许多专家学者对地铁运营中断下的应急车辆调度问题展开了大量的研究。
国内外许多专家学者对应急公交调度问题进行了研究,WANG等[1]设计了临时应急公交桥接网络,并实现了大规模的蒙特卡洛模拟试验;FENG[2]、GU[3]等提出了应急车辆可以灵活地服务于不同的桥接线路,来构建应急车辆调度优化模型;YANG等[4]对轨道交通网络在面对突发事件时的鲁棒性进行了度量,并提出了一种新的加权综合指数;TENG等[5]对乘客的行为和偏好进行了调查,并建立了一个多项式logit模型。YANG等[6]通过构建城市轨道交通与乘车平台之间的博弈模型,来优化城市轨道交通的补偿决策;WANG等[7]考虑了中断期间的动态客流,建立了多目标应急公交调度优化模型;胡华等[8]以完成各中断站乘客的总疏运时间最短为目标,构建公交车辆多循环调度模型;赵星等[9]以路阻函数的路径行程时间与基于大量历史交通量数据的可靠性为目标进行路径规划,并且通过指标权重确定最优路径;王勇[10]、吕伟[11]、柴获等[12]构建了考虑时间窗的车辆路径规划模型,并通过实例验证了模型的有效性;何民[13]、韩霜等[14]建立了响应式定制公交线路规划模型,并通过实例验证了模型和算法的可靠性;赵建有等[15]为提高突发事件下的救援效率,建立了应急物资配送优化模型;马昌喜等[16]针对疫情防控的要求,建立了突发事件下应急定制公交线路规划模型;薛浩楠等[17]提出了一种基于时空聚类法的定制公交需求响应机制,并通过实例验证了该响应机制的有效性。
上述研究主要是从固定线路调度角度出发,通过应急车辆循环往返疏运地铁中断站滞留的乘客。由于传统固定线路疏运不能有效地利用车辆自身的运能,因此本研究在以往研究的基础上,首先,从城市轨道交通运营中断下的实际操作模式出发,提出多停车场协同疏运以及多车型协调调度的作业模式。然后,针对传统固定线路调度疏运效率低的不足,提出了灵活调度策略,允许应急公交车辆服务于不同的调度路径。将车辆调度与线路规划整合为一个模型,以平均乘客延误最小和公交企业疏运成本最小为目标,建立了多车型下应急公交灵活线路开行方案模型。最后,采用改进的NSGA-Ⅱ算法对应急公交开行方案模型进行求解,从而高效合理的制定应急公交线路开行方案。
1 问题描述当城市地铁线路发生较长时间的运营服务中断事件时,应及时利用地面公交车辆对地铁中断站的乘客进行疏散。应急预案为:从距离地铁中断区间两端向外搜索最近的折返站,组织列车开行临时交路,而在中断区间内组织应急车辆来疏散滞留的乘客,同时选取中断区间内的站点作为应急公交临时停靠站。由于往返于中间站内的疏运需求一般相对较小,可借助其他交通工具继续出行,因此,本论文主要研究往返于折返站和中间站以及往返于折返站之间的待疏运客流需求。
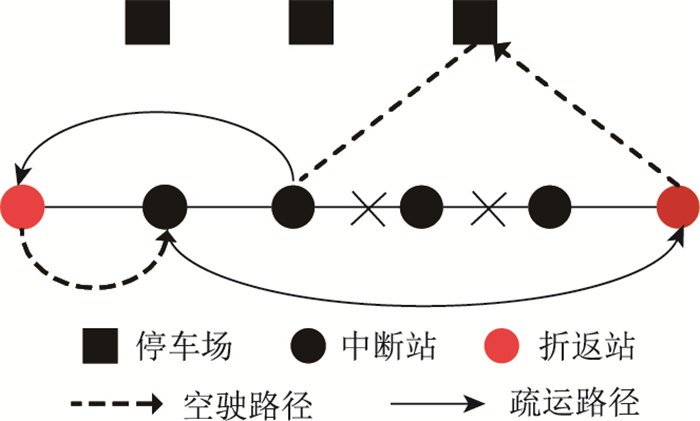
应急公交线路开行方案问题可描述为:已知某一中断区域内需要接驳的OD对集合为W,可供调度的停车场有s个,每个停车场有r辆k型车,每辆车的最大疏运次数为L,应急车辆每次只服务一个OD对,每个OD对的待疏运需求为Qia,由于疏运需求远超单辆车的运能,因此需要每辆应急公交车进行多次疏运,且可以灵活的服务不同的OD对。以企业疏运成本最少和乘客平均延误最小为目标,在所有乘客均被疏散的基础上,获取车辆的最佳调度方案和疏运路径,灵活接驳调度方案如图 1所示。
|
| 图 1 灵活接驳线路 Fig. 1 Flexible connection line |
| |
2 优化模型 2.1 模型假设
(1) 地铁中断站的待疏运乘客需求是确定的。
(2) 采用多车型协同调度,每种车型的额定载客量、车速、固定成本均不相同。
(3) 应急公交车辆完成疏运任务后需要返回原停车场。
(4) 应急车辆每次只能接驳1个OD对的乘客,期间不允许接驳其他乘客。
(5) 不考虑道路上各种突发事件对应急公交车辆的干扰。
2.2 参数和变量定义应急公交线路开行方案模型的相关参数和决策变量定义见表 1和表 2。
| 符号 | 定义 |
| I | 中断站集合, 且中断站i∈I |
| A | 折返站集合, 且折返站a∈A |
| K | 车型集合, 且车型k∈K |
| L | 应急公交车辆的最大疏运次数 |
| S | 停车场集合, 且停车场s∈S |
| Rsk | 停车场s的k型车辆集合, 且车辆rsk∈Rsk |
| Dsi | 停车场s到站点i的距离 |
| Das | 折返站a到停车场s的距离 |
| Dia | 应急公交站点i到折返站a的距离 |
| Dl, il-1, a | 第l-1次疏运与第l次疏运之间的空驶距离 |
| Qia | 中断站i到折返站a的待疏运乘客需求 |
| P | 标准车型的额定载客量 |
| δk | k型应急公交车辆的折算系数 |
| η | 应急公交车辆的最大满载率 |
| Vk | k型应急公交载客的平均运营速度 |
| V0k | k型应急公交车辆的空驶速度 |
| C1k | 单位k型车辆的固定成本 |
| C2k | 单位k型车辆的运营时间成本 |
| T | 乘客延误 |
| 决策变量 | 定义 |
| Xrsksk | 0-1变量,Xrsksk=1停车场s的第r辆k型车参加此次救援任务。 |
| Yiaskrskl | 0-1变量,Yiaskrskl=1停车场s的第r辆k型车的第l次疏运是从中断站i到折返站a。 |
| Lrsksk | 停车场s的第r辆k型车的实际疏运次数。 |
2.3 模型
为提高应急公交车辆的救援效率,本研究将车辆调度与线路规划整合为一个模型,以应急公交车辆的疏运成本Z1最小和平均乘客延误Z2最小为目标,构建了多目标应急公交线路开行方案模型。优化模型及约束条件如下:
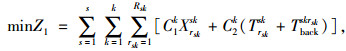
|
(1) |

|
(2) |
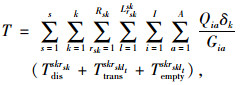
|
(3) |
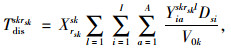
|
(4) |

|
(5) |
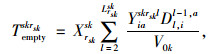
|
(6) |
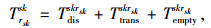
|
(7) |
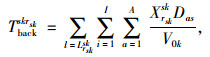
|
(8) |
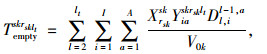
|
(9) |
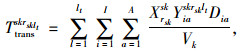
|
(10) |
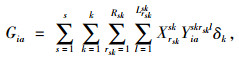
|
(11) |
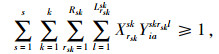
|
(12) |
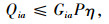
|
(13) |
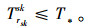
|
(14) |
式(1)为应急公交车辆疏运成本最小;式(2)为平均乘客延误最小;式(3)为乘客总延误的计算方法;式(4)每辆车被派遣到中断站的行驶时间;式(5)为每辆车在中断站间载客的行驶时间;式(6)为每辆车在执行任务期间的空驶时间;式(7)为每辆车的行驶时间;式(8)为车辆疏运完乘客返回停车场的空驶时间;式(9)为第lt次疏运车辆的累积空驶时间;式(10)为第lt次疏运车辆的累积载客时间;式(11)为服务某一OD的总车次数;式(12)为任一OD对均有车辆为其服务;式(13)为应急公交车辆疏运能力约束;式(14)为应急车辆的救援时间约束。
3 优化算法 3.1 NSGA-Ⅱ算法应急公交企业与出行乘客之间存在着一种博弈关系,针对应急突发事件乘客总是想要以最短的时间继续完成出行任务,而应急公交企业总是期望以最少的经济投入完成疏运任务,乘客与应急公交企业之间是相互竞争的,为了权衡不同目标之间的利益关系,需要得到一组Pareto解集。由于传统算法通常将多目标转化为单目标进行求解,常常存在算法早熟、局部最优以及权重不好确定等缺点。而快速非支配排序遗传算法(NSGA-Ⅱ),虽然相对复杂,但计算精度、优化效果较好。其搜索过程具有自组织、自学习性且运行一次能够得到一组互不支配的Pareto解集,因此选用NSGA-Ⅱ算法对应急公交线路开行方案模型进行求解。
3.2 NSGA-Ⅱ算法的改进 3.2.1 正态分布交叉算子由于普通NSGA-Ⅱ算法通常使用单点交叉,为了提升算法的搜索能力,在NSGA-Ⅱ算法中引入正态分布交叉算子[18]。令p1,p2为父代,利用正态分布算子产生x1,x2子代,其中|N(0, 1)|为正态分布随机变量,t为t∈(0, 1)内的随机数。
(1) 若t≤0.5
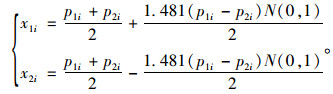
|
(15) |
(2) 若t>0.5
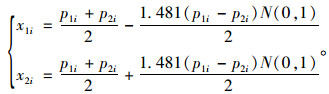
|
(16) |
由于普通NSGA-Ⅱ算法通常使用多项式变异策略,为了提高算法的局部搜索能力,采用差分变异策略对个体的进化过程进行干预,利用差分向量作为变异算子[18]。种群p的同一层级中相邻的父代个体{pa,pb}∈p,其子代个体p′i可通过差分变异算子获取,r为相邻个体对变异方向的影响程度r∈[0, 1],r越大影响越大。
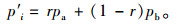
|
(17) |
Step 1:参数设置:输入算法相关参数,同时输入应急公交线路开行方案的相关参数。
Step 2:编码与解码:采用分段编码,获取每类车的使用数量、执行任务次数、优先级以及每次任务的优先级。解码,依据车辆的优先级安排每辆车执行任务的路径,依据当前车辆对于每个任务的优先级和执行任务次数,选择优先级高的任务作为本车的任务。
Step 3:随机生成初始种群,对于NSGA-Ⅱ算法设计的初始种群,将其转为约束条件,再把约束条件转换成边界条件,并在规定的边界中随机产生初始种群。
Step 4:使用锦标赛选择法对初始种群进行选择操作,并利用正态分布交叉算子和差分变异算子进行交叉和变异操作,从而形成子代个体。
Step 5:将父代和新产生的子代个体进行合并,依据拥挤度比较算子挑出新个体,并通过快速非支配排序以及拥挤度的计算产生新种群。
Step 6:算法终止条件判断,满足则终止运算,否则重复Step 3~Step 5。
4 案例分析 4.1 案例背景南昌地铁1号线是江西省南昌市首条开通运营的线路,途径经开区、红谷滩新区、东湖区、青山湖区、高新区,横跨赣江两岸,地理位置较独特,线路全长28.84 km,共修建24座车站,若彭家桥站-艾溪湖东站区段发生突发事件使线路双向运营中断,中断时间为2 h,涉及4个中间站和2个折返站,调用周边区域4个停车场来完成疏运任务。根据文献[8]的方法获取中断站的待疏运乘客需求如表 3所示,表 4为派车点的派车信息,表 5为车辆运营参数信息。
| 中断站 | D1 | D2 | D3 | D4 | D5 | D6 |
| A1 | 1 962 | 654 | 532 | 426 | 386 | 0 |
| A2 | 0 | 342 | 438 | 536 | 594 | 1824 |
| 派车点 | A型车 | B型车 | D1 | D2 | D3 | D4 | D5 | D6 |
| S1 | 5 | 5 | 5.2 | 5.8 | 6.4 | 7.5 | 8.8 | 10.8 |
| S2 | 5 | 5 | 8.7 | 7.9 | 7.1 | 6 | 5.4 | 7.4 |
| S3 | 5 | 5 | 6.6 | 5.8 | 5 | 6.1 | 7.4 | 9.4 |
| S4 | 5 | 5 | 10.6 | 9.8 | 9 | 7.9 | 6.6 | 6.2 |
| 参数配置 | A型车 | B型车 |
| 额定载客量/人 | 70 | 50 |
| 空驶速度/(km·h-1) | 25 | 30 |
| 载客运营速度/(km·h-1) | 21 | 26 |
| 单位时间运营成本/(元·h-1) | 200 | 160 |
| 单位车辆固定成本/(元·veh-1) | 300 | 210 |
4.2 优化结果分析
固定线路调度方案指应急公交车辆从派车场出发前往中断站点,沿中断站行驶到折返站,且在折返站清客后直接空驶返回原中断站进行下一次疏运或停止疏运返回原停车场。利用改进的NSGA-Ⅱ算法对应急公交车辆固定调度模型与灵活调度模型进行求解,并采用隶属度函数求解出最大满意度的Pareto解,从而得到应急公交开行方案的最优折衷解。表 6为不同调度方案对比结果,表 7为灵活调度方案的优化结果。
| 调度方案 | 固定调度 | 灵活调度 | 变化率% |
| 平均乘客延误/(h·人-1) | 0.981 | 0.930 | -5.20 |
| 疏运成本/元 | 21 509 | 13 798 | -35.85 |
| 参与调度车辆数/veh | 47 | 32 | -31.91 |
| 方案 | 1#车 | 2#车 | 3#车 | 4# | 5#车 | |
| 停车场1 | A型车 | 1, 6;6, 1;2, 6;6, 1 | 1, 6;6, 1;2, 6;6, 1 | 1, 6;6, 1;2, 6;6, 1 | 1, 6;6, 1;2, 6;6, 1 | — |
| B型车 | 1, 6;4, 1;2, 1;3, 1;2, 6 | 1, 6;4, 1;2, 1;3, 1;2, 6 | — | — | — | |
| 停车场2 | A型车 | 4, 1;3, 6;6, 1;1, 6 | 4, 1;3, 6;6, 1;1, 6 | 4, 1;3, 6;6, 1;1, 6 | — | — |
| B型车 | 5, 1;3, 6;5, 1;2, 6;4, 6 | 4, 6;4, 6;4, 6;4, 6;4, 6 | 4, 6;4, 6;5, 6;5, 6;5, 6 | 5, 6;5, 6;5, 6;5, 6;5, 6 | — | |
| 停车场3 | A型车 | 1, 6;6, 1;3, 1;1, 6;5, 1 | 1, 6;6, 1;3, 1;1, 6;5, 1 | 1, 6;6, 1;3, 1;1, 6;5, 1 | 1, 6;6, 1;3, 1;1, 6;5, 1 | 1, 6;6, 1;3, 1;1, 6;5, 1 |
| B型车 | 1, 6;6, 1;2, 1;2, 6;5, 1 | 1, 6;6, 1;2, 1;2, 6;5, 1 | 1, 6;6, 1;2, 1;2, 6;5, 1 | 2, 1;2, 1;2, 6;2, 6;4, 1 | 4, 1;4, 1;4, 1;4, 1;4, 6 | |
| 停车场4 | A型车 | 6, 1;1, 6;6, 1;1, 6;3, 6 | 6, 1;1, 6;6, 1;1, 6;3, 6 | 6, 1;1, 6;6, 1;1, 6;3, 6 | 6, 1;1, 6;6, 1;1, 6;3, 6 | — |
| B型车 | — | — | — | — | ||
表 6、表 7结果表明:应急公交车辆在每次完成疏运任务后,能够就近或者直接服务包含本次疏运任务终点的其他OD对,能够弥补传统固定线路调度回程空驶返回原起点不载客的不足;灵活调度方案相比固定调度方案平均乘客延误降低了5.20%, 应急公交疏运成本降低了35.85%,参与调度的车辆数降低了31.91%;同时,也验证应急公交灵活线路调度方案的优越性。
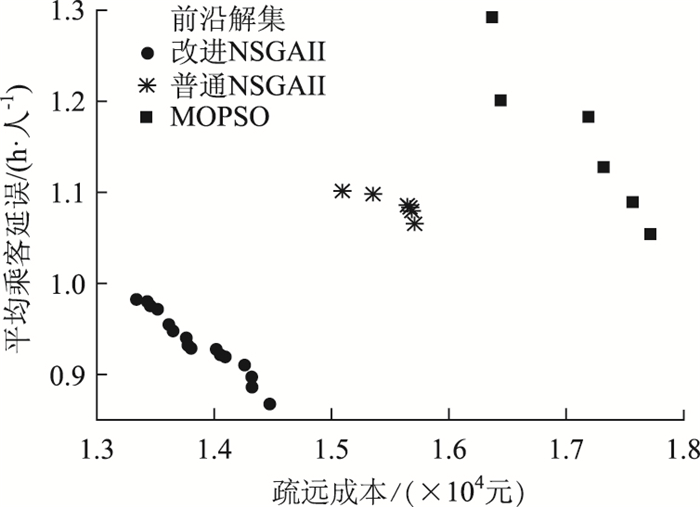
4.3 算法分析为了验证改进的NSGA-Ⅱ算法与普通NSGA-Ⅱ算法以及多目标粒子群算法(MOPSO)的收敛精度和搜索能力,在相同试验数据的条件下进行试验,来对比3种算法的优化效果,表 8为优化结果,图 2为优化效果对比图。
| 方案 | 粒子群MOPSO | 普通NSGA-Ⅱ | 改进NSGA-Ⅱ |
| 平均乘客延误/(h·人-1) | 1.183 | 1.102 | 0.930 |
| 疏运成本/元 | 17 192 | 15 090 | 13 798 |
|
| 图 2 算法效果对比 Fig. 2 Contrast of algorithm effectd |
| |
图 2、表 8结果表明:改进NSGA-Ⅱ算法相比普通NSGA-Ⅱ算法具有较高的计算精度和搜索能力,且求得的Pareto最优解集分布更均匀;同时,NSGA-Ⅱ算法相比MOPSO算法具有较高的计算精度和搜索能力。
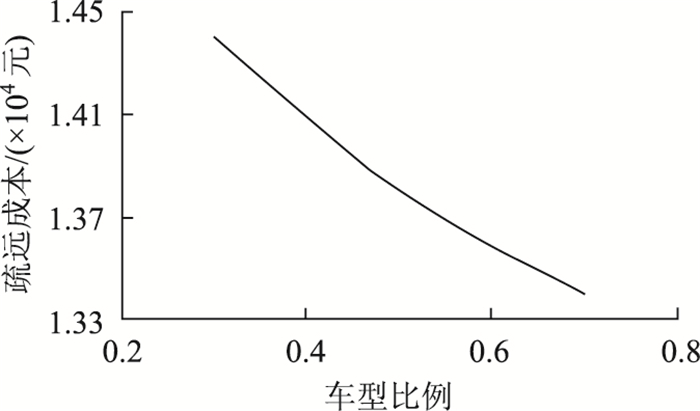
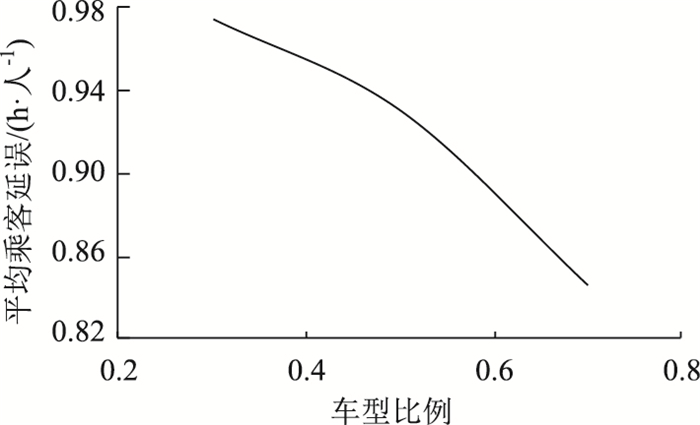
4.4 灵敏度分析对应急公交车辆的车型比例(B型车数量/总车数量)进行灵敏度分析,研究B型车数量的变化对应急公交线路开行方案的影响,图 3、图 4分别为应急公交疏运成本和平均乘客延误随车型比例的变化情况。
|
| 图 3 疏运成本-车型比例 Fig. 3 Ratio of evacuation cost to vehicle type |
| |
|
| 图 4 平均乘客延误-车型比例 Fig. 4 Ratio of average passenger delay to vehicle type |
| |
图 3、图 4结果表明:在一定范围内应急公交疏运成本、平均乘客延误随车型比例的增加而下降车,车型比例对应急公交调度方案具有显著影响。
5 结论(1) 在地铁运营中断条件下,考虑到传统固定线路调度方案疏运效率低的问题,本研究将车辆调度与线路规划问题集成一个模型,构建了多车型下的应急公交线路开行方案模型,并利用改进的NSGA-Ⅱ算法对开行方案模型求解。
(2) 以南昌地铁1号线为例进行分析,研究结果表明:灵活调度方案相比传统固定调度方案,平均乘客延误降低了5.20%,应急公交疏运成本降低了35.85%,参与调度的车辆数降低了31.91%;同时对车型比例进行灵敏度分析,发现车型比例对调度方案具有显著影响。
(3) 论文仅研究了单条地铁线路运营中断下的应急公交线路开行方案,而目前各大城市地铁网络迅速发展,研究大型中断网络下的应急公交线路开行方案将是接下来研究的重点。
| [1] |
WANG Y B, GUO J Q, CURRIE G, et al. Bus Bridging Disruption in Rail Services with Frustrated and Impatient Passengers[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2014-2023. |
| [2] |
QIU F, LI W, HAGHANI A. A Methodology for Choosing between Fixed-route and Flex-route Policies for Transit Services[J]. Journal of Advanced Transportation, 2015, 49(3): 496-509. |
| [3] |
GU W, YU J, JI Y, et al. Plan-based Flexible Bus Bridging Operation Strategy[J]. Transportation Research Part C: Emerging Technologies, 2018, 91(7): 209-229. |
| [4] |
YANG Y H, LIU Y X, ZHOU M X, et al. Robustness Assessment of Urban Rail Transit Based on Complex Network Theory: A Case Study of the Beijing Subway[J]. Safety Science, 2015, 79: 149-162. |
| [5] |
TENG J, LIU W R. Development of a Behavior-based Passenger Flow Assignment Model for Urban Rail Transit in Section Interruption Circumstance[J]. Urban Rail Transit, 2015, 1(1): 35-46. |
| [6] |
YANG J F, JIN J G, WU J. Optimizing Passenger Flow Control and Bus-bridging Service for Commuting Metro Lines[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(6): 458-473. |
| [7] |
WANG J D, YUAN Z Z, YIN Y H. Optimization of Bus Bridging Service under Unexpected Metro Disruptions with Dynamic Passenger Flows[J]. Journal of Advanced Transportation, 2019, 2019: 6965728. |
| [8] |
胡华, 高云峰, 刘志钢, 等. 地铁运营中断下公交桥接疏运车辆应急调度模型及算法[J]. 铁道学报, 2018, 40(5): 31-37. HU Hua, GAO Yun-feng, LIU Zhi-gang, et al. Model and Algorithm for Bridging Bus Emergency Dispatching Problem during Metro Operational Disruptions[J]. Journal of the China Railway Society, 2018, 40(5): 31-37. |
| [9] |
赵星, 吉康, 林灏, 等. 基于多目标路径规划的应急资源配置模型[J]. 华南理工大学学报: 自然科学版, 2019, 47(4): 76-82. ZHAO Xing, JI Kang, LIN Hao, et al. Resource Allocation Model Based on Multi-objective Path Planning in Emergency Management[J]. Journal of South China University of Technology: Natural Science Edition, 2019, 47(4): 76-82. |
| [10] |
王勇, 黄秋彬, 刘永, 等. 基于客户重要度的混合时间窗车辆路径问题研究[J]. 公路交通科技, 2019, 36(11): 151-158. WANG Yong, HUANG Qiu-bin, LIU Yong, et al. Study on Vehicle Routing Problem with Mixed Time Windows Based on Importance of Customers[J]. Journal of Highway and Transportation Research and Development, 2019, 36(11): 151-158. |
| [11] |
吕伟, 李志红, 马亚萍, 等. 考虑受灾点需求时间窗的应急物资配送车辆路径规划研究[J]. 中国安全生产科学技术, 2020, 16(3): 5-11. LÜ Wei, LI Zhi-hong, MA Ya-ping, et al. Research on Route Planning of Emergency Materials Distribution Vehicles Considering Time Window of Requirements by Disaster Point[J]. Journal of Safety Science and Technology, 2020, 16(3): 5-11. |
| [12] |
柴获, 何瑞春, 苏江省, 等. 求解双目标带时间窗车辆路径问题的蚁群算法[J]. 交通运输系统工程与信息, 2018, 18(4): 156-162. CHAI Huo, HE Rui-chun, SU Jiang-sheng, et al. An Ant Colony Optimization for the Bi-objective Vehicle Routing Problem with Time Windows on Mutilgraph[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(4): 156-162. |
| [13] |
何民, 李沐轩, 税文兵, 等. 可靠性和舒适性对响应式定制公交线路设计的影响[J]. 公路交通科技, 2019, 36(5): 145-151. HE Min, LI Mu-xuan, SHUI Wen-bing, et al. Influence of Reliability and Comfort on Responsive Custom Bus Route Design[J]. Journal of Highway and Transportation Research and Development, 2019, 36(5): 145-151. |
| [14] |
韩霜, 傅惠. 即时响应式定制公交调度优化[J]. 公路交通科技, 2020, 37(6): 120-127, 158. HAN Shuang, FU Hui. Optimization of Real-time Responsive Customized Bus Dispatch[J]. Journal of Highway and Transportation Research and Development, 2020, 37(6): 120-127, 158. |
| [15] |
赵建有, 韩万里, 郑文捷, 等. 重大突发公共卫生事件下城市应急医疗物资配送[J]. 交通运输工程学报, 2020, 20(3): 168-177. ZHAO Jian-you, HAN Wan-li, ZHENG Wen-jie, et al. Distribution of Emergency Medical Supplies in Cities under Major Public Health Emergency[J]. Journal of Traffic and Transportation Engineering, 2020, 20(3): 168-177. |
| [16] |
马昌喜, 王超, 郝威, 等. 突发公共卫生事件下应急定制公交线路优化[J]. 交通运输工程学报, 2020, 20(3): 89-99. MA Chang-xi, WANG Chao, HAO Wei, et al. Emergency Customized Bus Route Optimization under Public Health Emergencies[J]. Journal of Traffic and Transportation Engineering, 2020, 20(3): 89-99. |
| [17] |
薛浩楠, 王佳. 基于时空聚类的定制公交需求响应机制[J]. 公路交通科技, 2021, 38(3): 113-121. XUE Hao-nan, WANG Jia. Demand Response Mechanism of Customized Bus Based on Space-time Clustering[J]. Journal of Highway and Transportation Research and Development, 2021, 38(3): 113-121. |
| [18] |
傅生辉, 李臻, 杜岳峰, 等. 基于改进NSGA-Ⅱ算法的拖拉机传动系统匹配优化[J]. 农业机械学报, 2018, 49(11): 349-357. FU Sheng-hui, LI Zhen, DU Yue-feng, et al. Matching Optimization for Tractor Powertrain Based on Improved NSGA-Ⅱ Algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(11): 349-357. |
 2021, Vol. 38
2021, Vol. 38
